I strongly recommend visiting the year 1 notes before delving into the 2nd year notes
The Language of Thermodynamics
¶ Mole Fractions
The mole fraction is defined as the ratio of the amount of a component to the total amount of substance
- Since the mole fraction is a ratio, it must have a value between and
- Moreover, the sum of all mole fractions must equal
There are three types of mole fractions we have to deal with
- Mole fraction of overall composition
- Mole fraction in liquid phase
- Mole fraction in vapour phase
¶ Pressure and Mixing
Before we dive into the discussion of mixing, we must first familiarize ourselves with different relations concerning pressure
¶ Partial Pressure
The pressure exerted by an individual gas in a mixture is known as its partial pressure
- We can think of the partial pressure as the pressure each gas would exert if it alone occupied the volume of the mixture at the same temperature
According to Dalton's law of partial pressures, the total pressure by a mixture of gases is equal to the sum of the partial pressures of each of the constituent gases
- Dalton's Law is applicable to ideal gas and is a very good approximation for real gaseous mixture that do not react together
- Dalton's Law is an empirical law
Justification for Dalton's Law
- An ideal gas will expand to fill the container it is in without affecting the pressure of another gas
- So it can be concluded that the pressure of a certain gas is based on the number of moles of that gas and the volume and temperature of the system. Since the gases in a mixture of gases are in one container, the Volume (V) and Temperature (T) for the different gases are the same as well
- Each gas exerts its own pressure on the system, which can be added up to find the total pressure of the mixture of gases in a container
We can also relate the total pressure and the partial pressure of a component using the mole fraction
¶ Vapour Pressure
The pressure exerted by the gas in equilibrium with a solid or liquid in a closed container at a given temperature is called the vapor pressure
- Vapor pressure is the partial pressure exerted when a component is in vapor phase
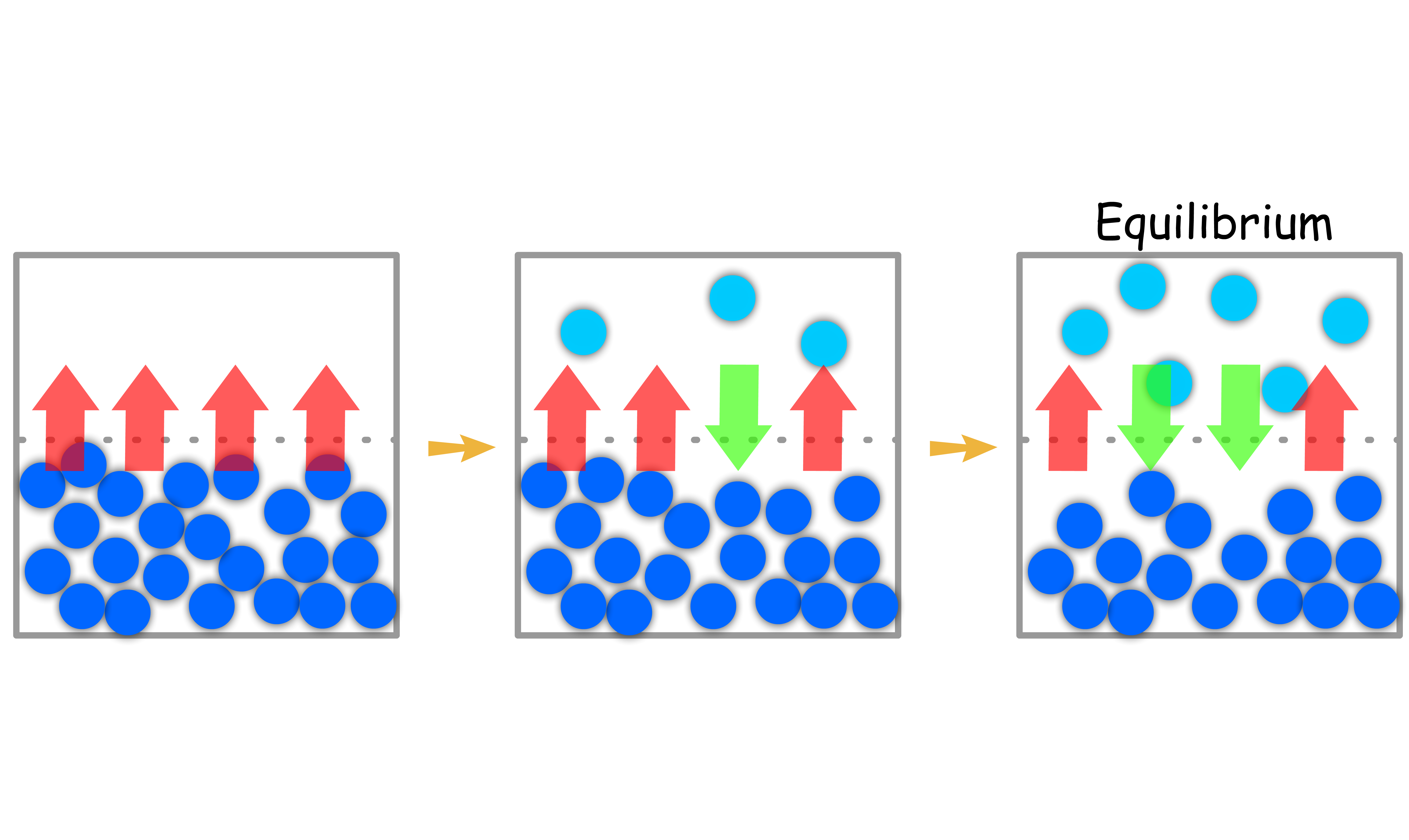
Suppose we have a pure condensed phase ( liquid or solid ) within a container
- The molecules will constantly be leaving the condensed phase to go into the vapor phase and vapor will re-condense back into the condensed phase
- If this is a close system, we will eventually reach an equilibrium where the rate of vaporization is equal to the rate of condensation
- The vapor in this equilibrium state will be able to exert pressure to the container or surrounding, this is called the vapor pressure
Whether the liquid will boil depends on its relative magnitude to the external pressure
- As long as the external pressure is larger than the vapor pressure, it will be favorable for some molecules to stay in the liquid phase
- At the point when the vapor pressure equals the external pressure, all liquid molecules can start to spontaneously go into the gas phase, this is called the boiling point
Since the vapor pressure is the pressure exerted at equilibrium, we can change the vapor pressure by changing the equilibrium position. This can be achieved by changing the temperature
- The relation between vapor pressure and the temperature can be found from the phase diagram
¶ Ideal Mixing
There are two types of ideal mixtures, ideal gaseous mixtures and ideal solutions
- The ideality of solution is not the same as that of a gaseous mixture
Fundamentally, the process of mixing is ideal when the corresponding change in enthalpy is zero
- In other words, there is no net change in bond enthalpy upon mixing
- Put another way, the intermolecular interactions between the pure substance is the same as that of the mixture
Even without any knowledge in thermodynamics, we should know that mixing is a spontaneous process
- At constant pressure and temperature, spontaneous processes are indicated by a decrease in Gibbs energy
- The change in Gibbs energy can be expressed as such
- By definition, the change in enthalpy for ideal mixing is zero, so the decrease in Gibbs energy, and hence the spontaneity of mixing, must be solely contributed by entropy
- The entropy of a mixture must be greater than the sum of the entropy of the pure components
¶ Ideal Gaseous Mixtures
An ideal gas is a hypothetical gas whose molecules occupy negligible space and have no interactions
- There is no intermolecular interaction between ideal gas molecules, be it attraction or repulsion. In other words, there is no bonding between the molecules
- The absence in intermolecular bonding of pure ideal gas means that there won't be any intermolecular interaction within a mixture of ideal gas either
- There is no intermolecular bonding in both the pure ideal gas and the ideal gaseous mixture, which means that no bond is broken or formed in the process of mixing
- Put another way, the enthalpy of mixing ideal gases is zero, which is consistent with the definition of ideal mixture
ΔGmix of Ideal Gaseous Mixture
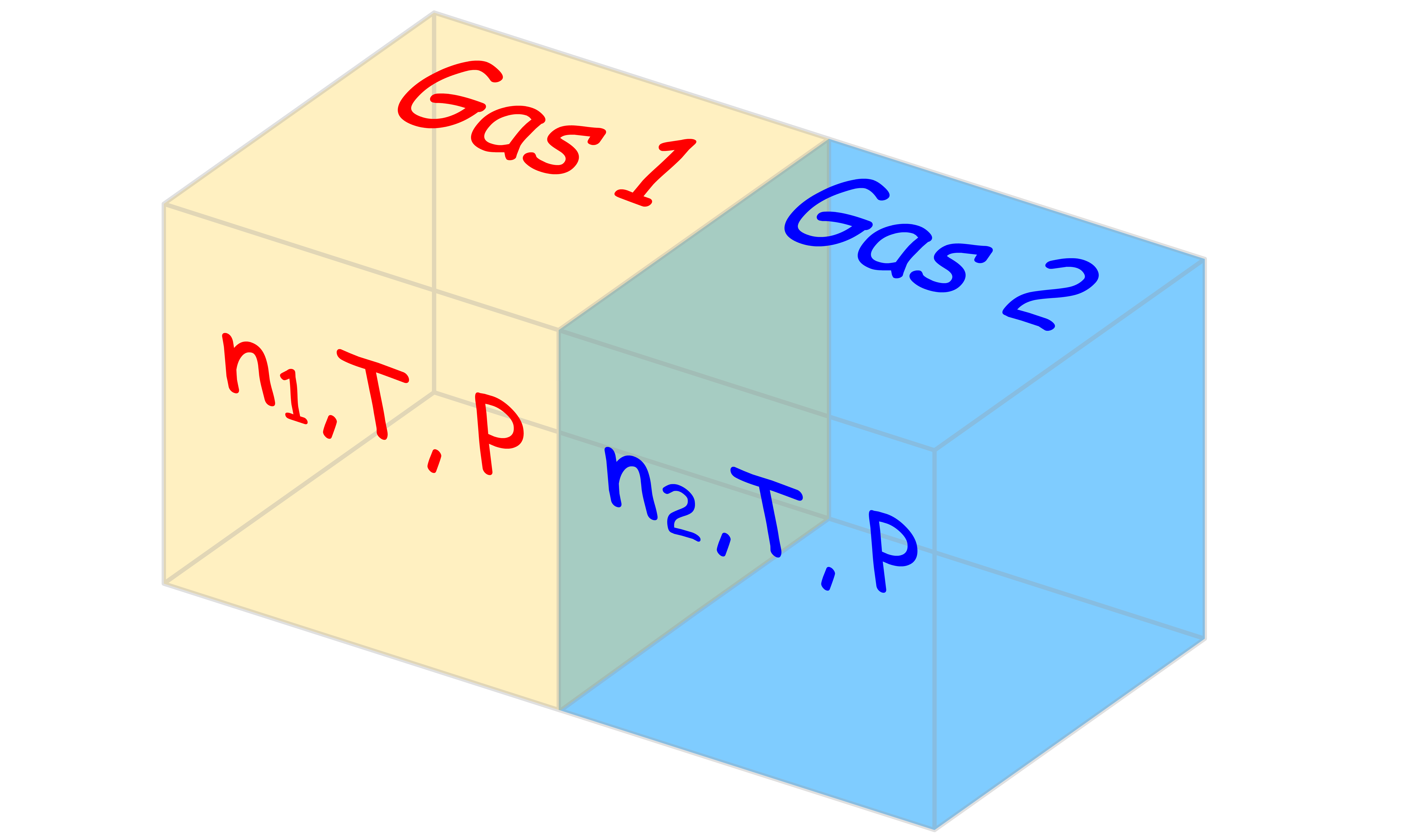
Consider the following situation:
Initially there are two pure gaseous components present in a container, separated by a gate
- The system is in equilibrium, so the temperature and pressure on both sides are the same. Hence, the chemical potential for each compartment is given by
- The initial Gibbs energy of the system is the sum of chemical potential of each compartment multiplied by their corresponding mole number
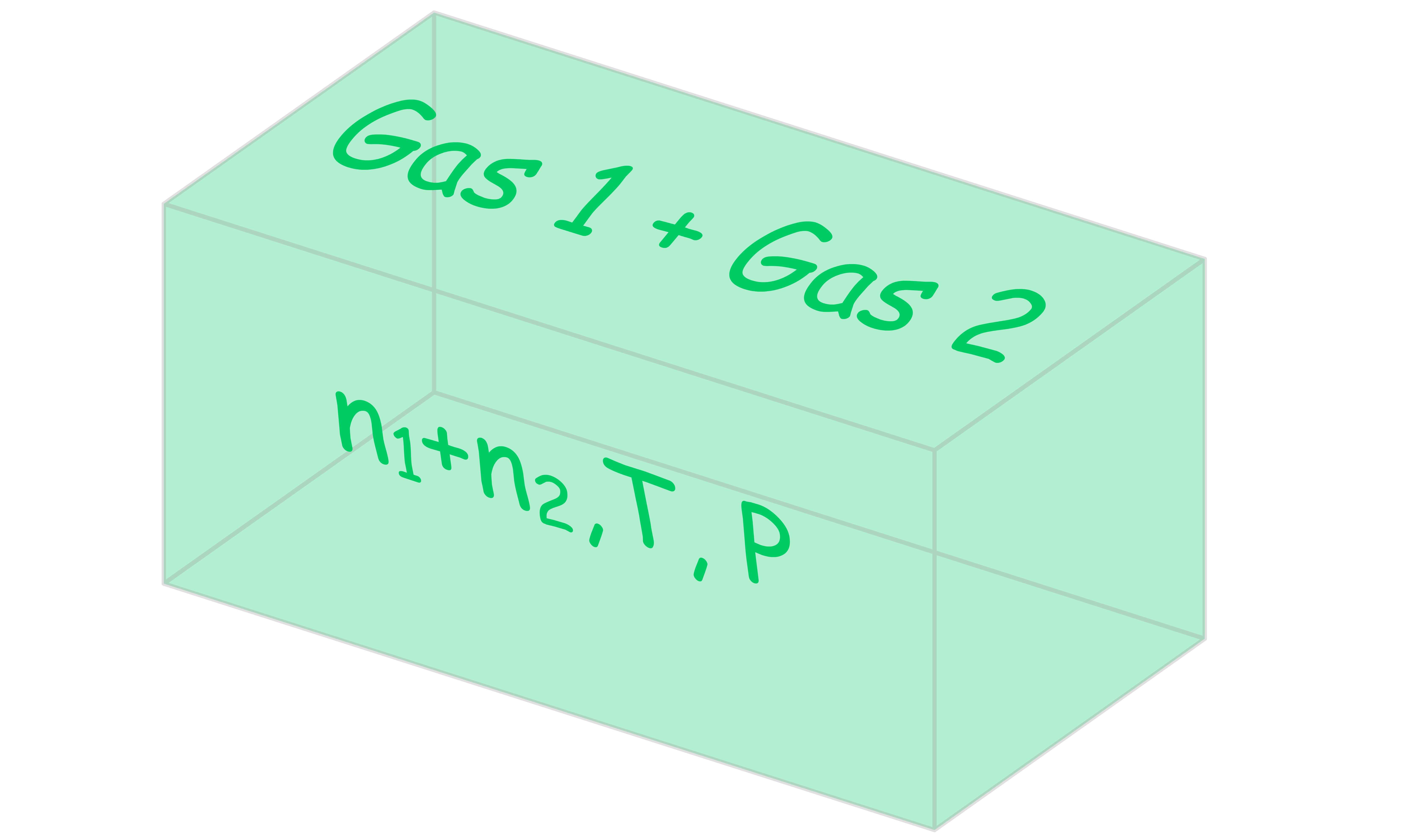
The gate is then opened and the two gases are allowed to mix
- Since there was no temperature or pressure gradient before the gate was open, the temperature and pressure should still be the same after the mixing of gases
- Moreover, the total pressure is now the sum of the partial pressures, . Hence, the chemical potential for each compartment is given by
- The final Gibbs energy of the system is the sum of the final chemical potential of each gas multiplied by their corresponding mole number
The change in Gibbs energy tells us whether this process is spontaneous
- By definition, the change in Gibbs energy, is found by subtracting the initial Gibbs energy from the final Gibbs energy
- Substituting and with the expressions we derived above
- With a little bit of algebaric manipulation, we will get
- Using the relation between mole fraction and total mole number, and the relation between partial pressure and total pressure, , we can rewrite the equation to
- Since mole fractions are never greater than one, the logarithms in the equation are negative, thus making
- The conclusion that is negative for all compositions confirms that perfect gases mix spontaneously at all proportions
¶ Ideal Solutions
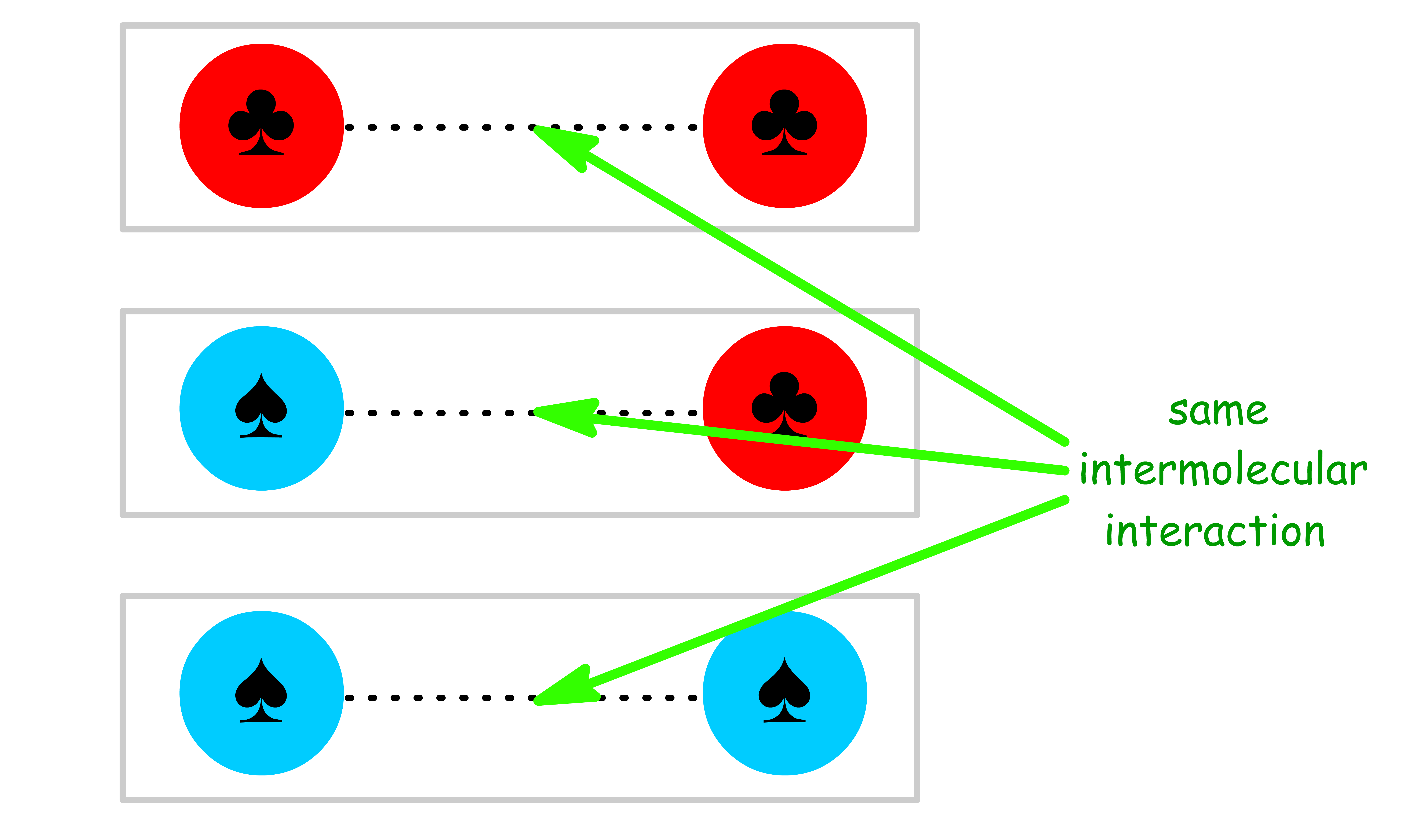
An ideal solution is a solution where the intermolecular interaction between the same species is the same as the intermolecular interaction between the different species
- In other words, the molecules of various species within an ideal solution are so similar to one another that replacing molecules of one species with molecules of another species will not change the spatial structure or intermolecular interaction energy in the solution
To understand the definition of an ideal solution, let us consider a solution with two species ( and )
- The and molecules must be essentially of the same size and shape such that there is no change in spatial structure upon mixing
- The intermolecular interaction between , and must be the same
The intermolecular bonding within the pure liquid is the same as that of the ideal solution, which means that there is no net bond breaking or formation in the process of mixing
- Put another way, the enthalpy of mixing ideal solution is zero, which is consistent with the definition of ideal mixture
To quantitatively define ideal solution, we shall resort to Raoult's Law
- Raoult's Law sates that the vapour pressure of each component of an ideal mixture of liquids is equal to the vapor pressure of the pure component ( liquid or solid ) multiplied by its mole fraction in the mixture
- We can combine it with Dalton's Law to get the expression
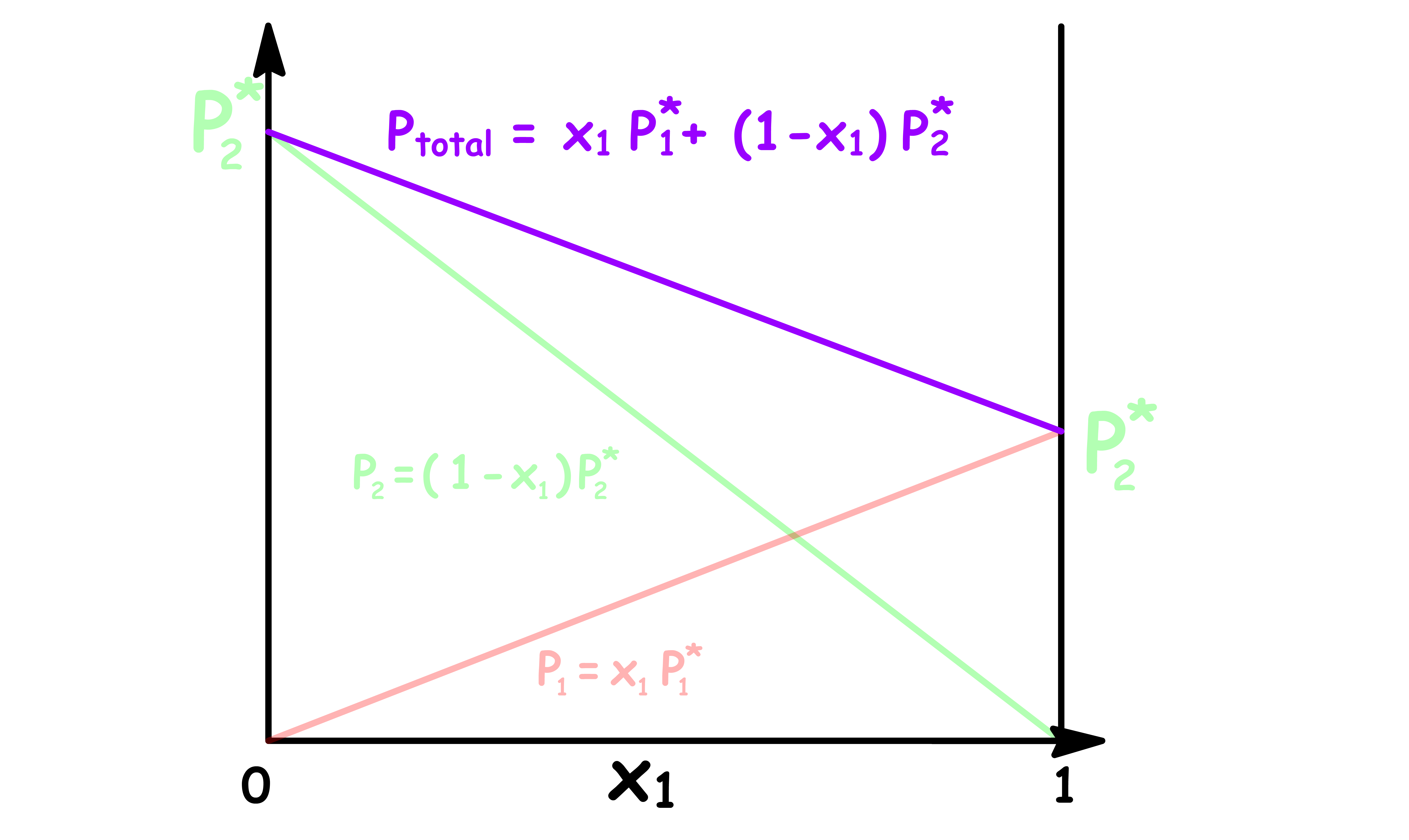
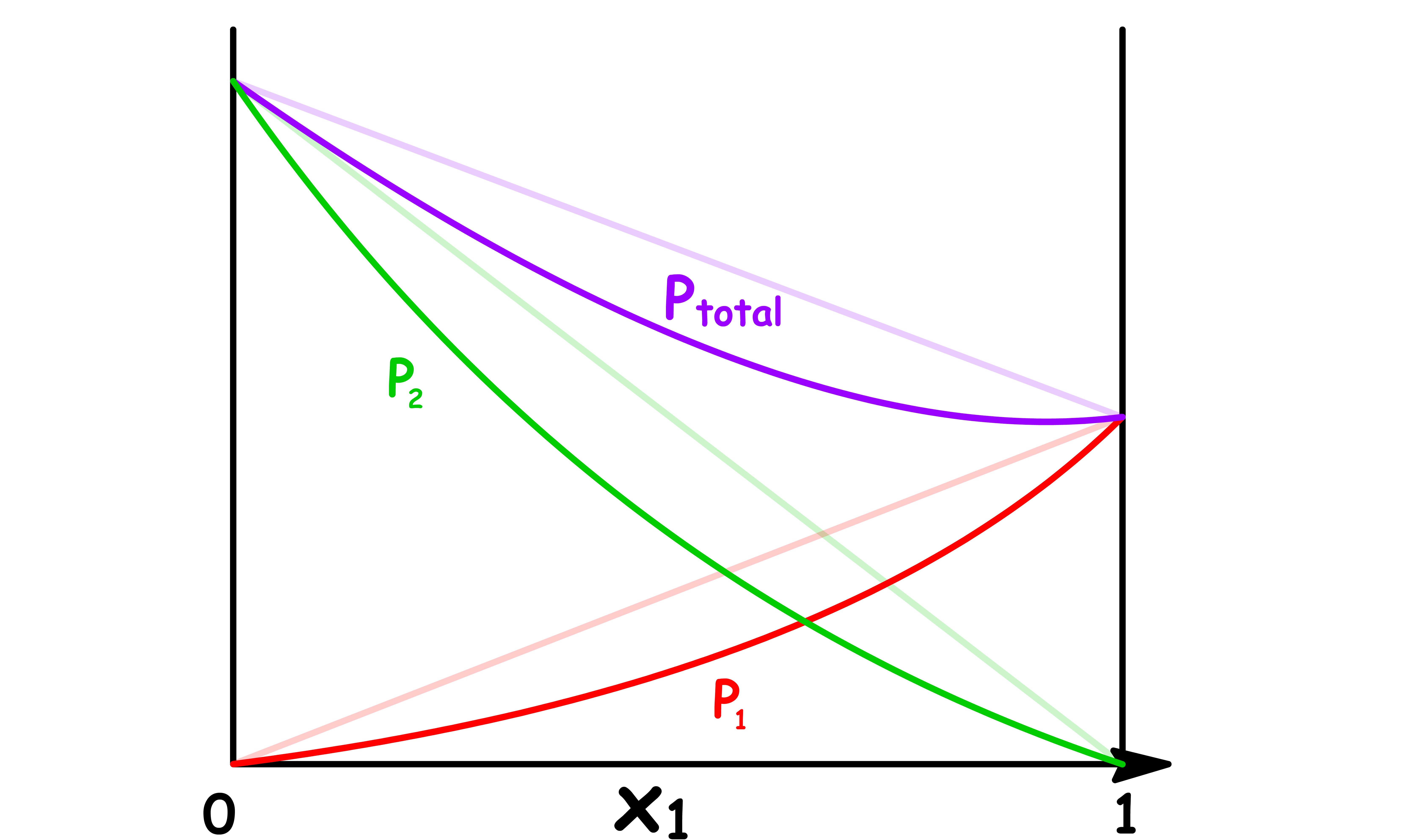
We can therefore determine whether a solution is ideal or not simply by examining how the total vapour pressure changes with mole fraction
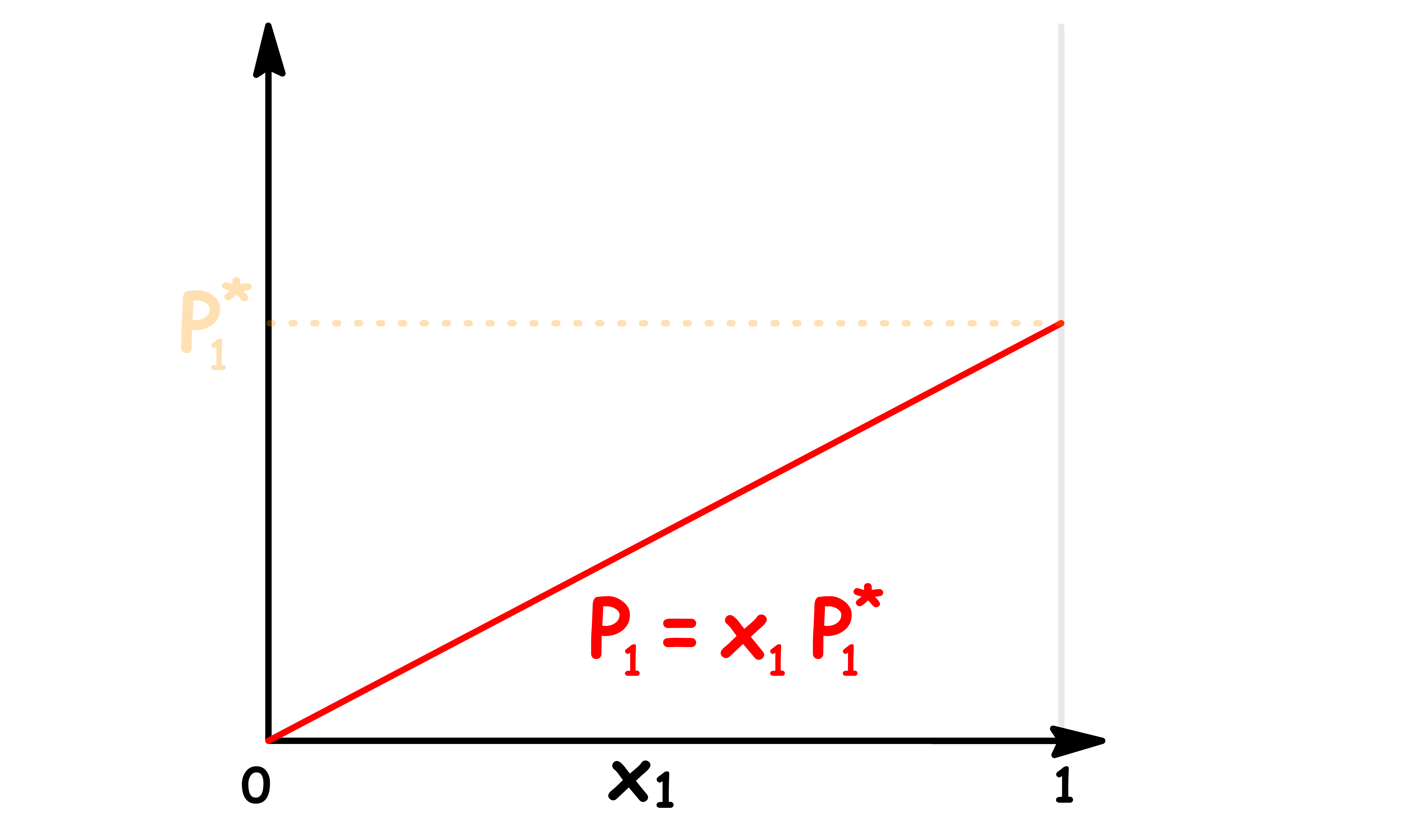
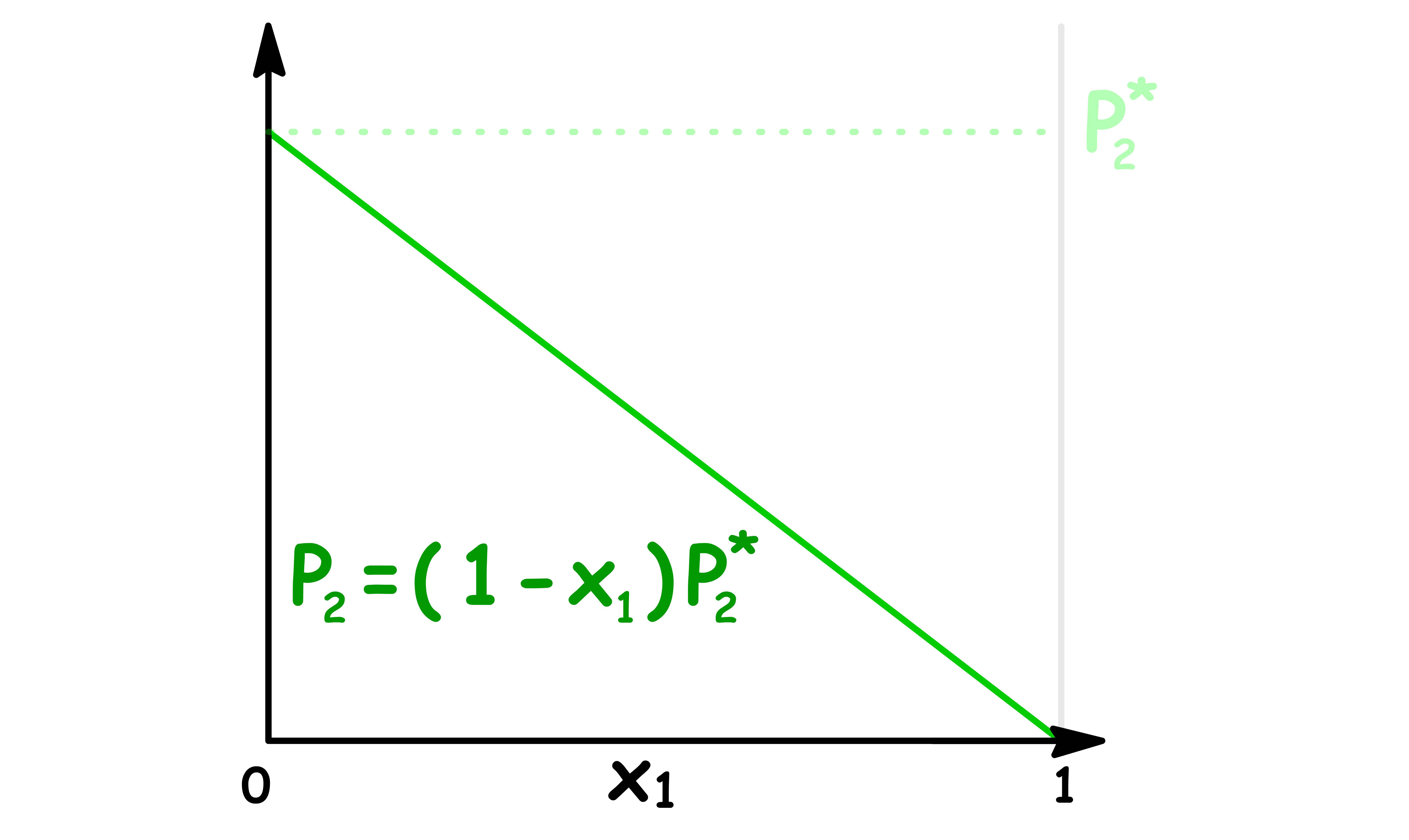
Let us consider an ideal solution that only contains two components
- The vapour pressure of component 1 increases linearly as the mole fraction of component 1 increases
- In a two components system, the mole fraction of component 2 is given by , so the vapour pressure of component 2 decreases linearly as the mole fraction of component 1 increases
The total vapour pressure is the sum of the two vapour pressures, so we can plot it out
We shall denote quantities relating to pure substances by a superscript *
¶ The Chemical Potential of liquids and Solutions
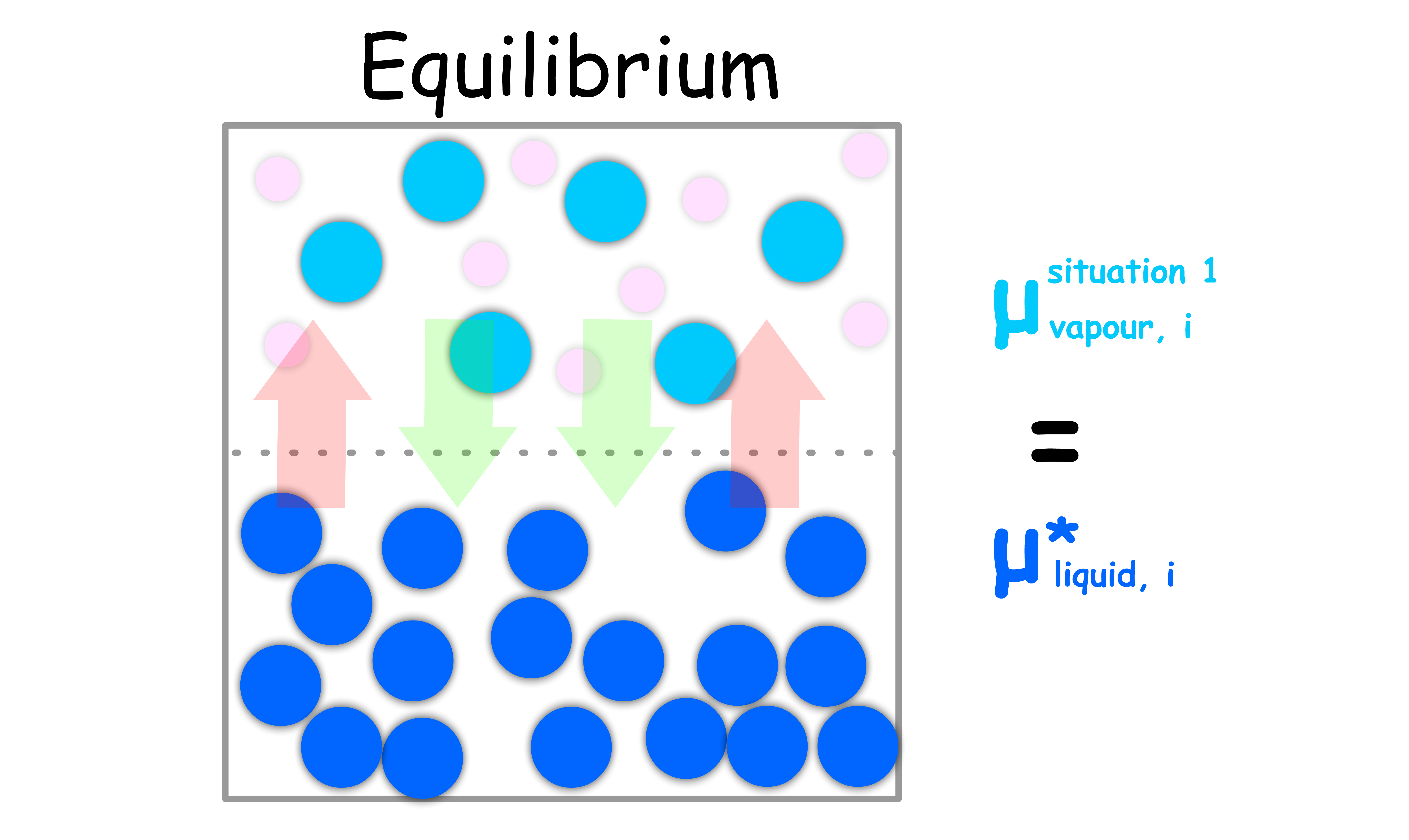
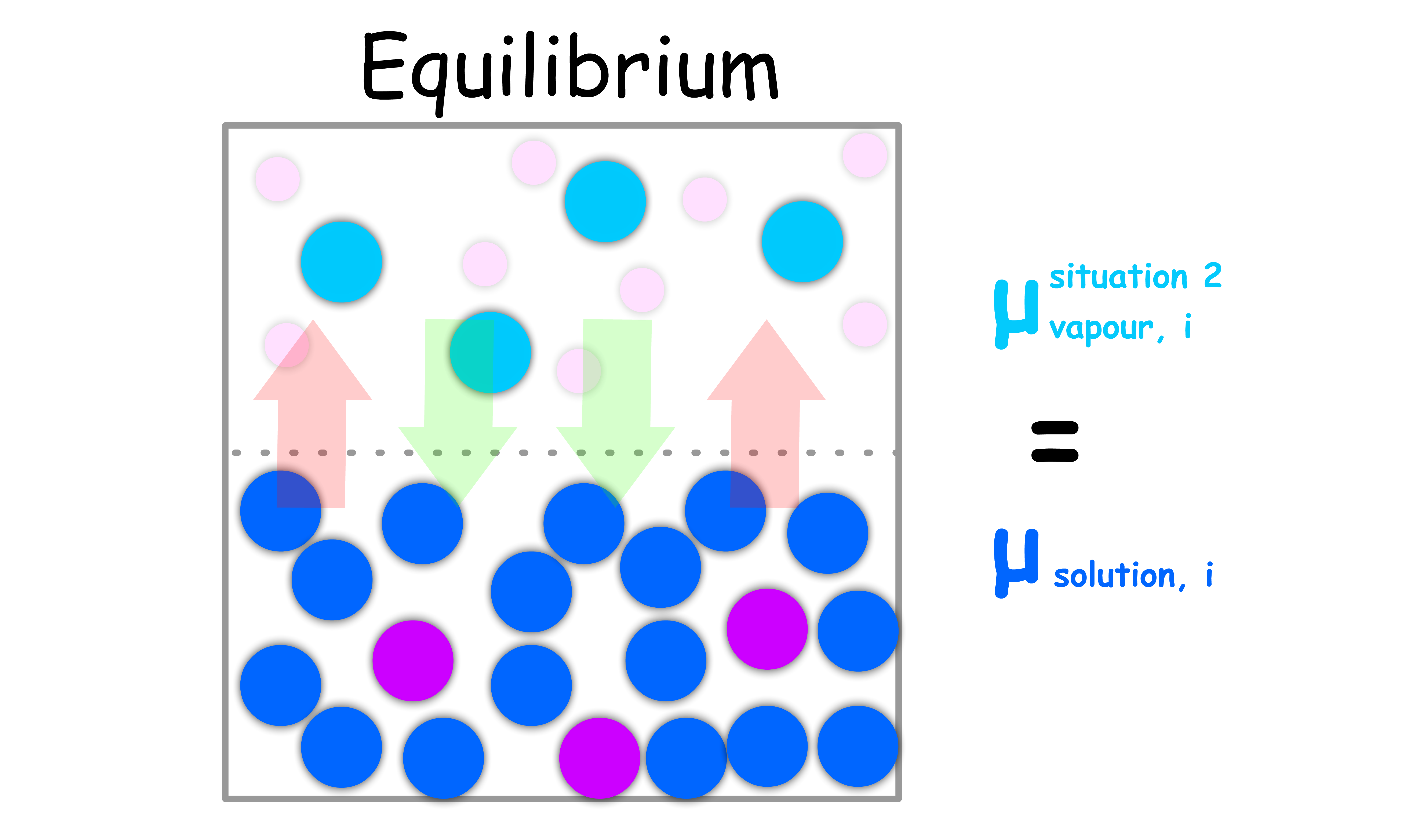
Situation 1: Consider a system of pure liquid, the vapour of said liquid and some other inert gases
- When the system is in equilibrium, the chemical potential of the vapour must be the same as that of the pure liquid
- If the vapour and the inert gases follow the ideal-gas law, the chemical potential of the vapour can be expressed as such
- Since the chemical potential of the vapour must be the same as that of the pure liquid at equilibrium, we can write
Situation 2: Consider the same system, but there is more than one component in the liquid phase
- When the system is in equilibrium, the chemical potential of the vapour must be the same as that of the liquid in the solution
- If the vapour and the inert gases follow the ideal-gas law, the chemical potential of the vapour can be expressed as such
- Since the chemical potential of the vapour must be the same as that of the liquid in solution at equilibrium, we can write
The Chemical Potential of a Component in Solution
Although we have already come up with an expression for the chemical potential of a component, it will be more convenient if we can express it in terms of
- To achieve that, we simply have to combine the equations obtained from each situation
- If we subtract the equations, we can eliminate the standard chemical potential of the gas
- A little bit of algebaric manipulation allows us to rewrite the equation as such
- Since we are working with ideal solutions, we can use Raoult's Law, to rewrite the equation
- For simplicity's sake, we can express it as such
¶ ΔGmix of Ideal Solutions
Consider the following situation:
Initially there are two pure liquid components present in a container, separated by a gate
- The initial Gibbs energy of the system is the sum of chemical potential of each compartment multiplied by their corresponding mole number
The gate is then opened and the two liquids are allowed to mix
- The initial Gibbs energy of the system is the sum of chemical potential of each component multiplied by their corresponding mole number
The change in Gibbs energy tells us whether this process is spontaneous
- By definition, the change in Gibbs energy, is found by subtracting the initial Gibbs energy from the final Gibbs energy
- Substituting and with the expressions we derived above
- Using the relation between mole fraction and total mole number, , we can rewrite the equation to
- Since mole fractions are never greater than one, the logarithms in the equation are negative, thus making
- The conclusion that is negative for all compositions confirms that the mixing of pure liquids to form ideal solution is spontaneous at all proportions
¶ Non-Ideal Mixing
In contrast to ideal mixing, real mixing do bring about a change in enthalpy
- In other words, there is a net change in bond enthalpy upon mixing
- Put another way, the intermolecular interactions between the pure substance is NOT the same as that of the mixture
Unlike ideal mixtures, formation of non-ideal mixtures may or may not be spontaneous
- At constant pressure and temperature, spontaneity is indicated by the change in Gibbs energy
- From studying ideal mixtures, we know that must be greater than zero, which means the second term must be negative
- The magnitude and sign of , and hence the spontaneity of forming real mixtures, depends on the magnitude and sign of
¶ ΔmixH
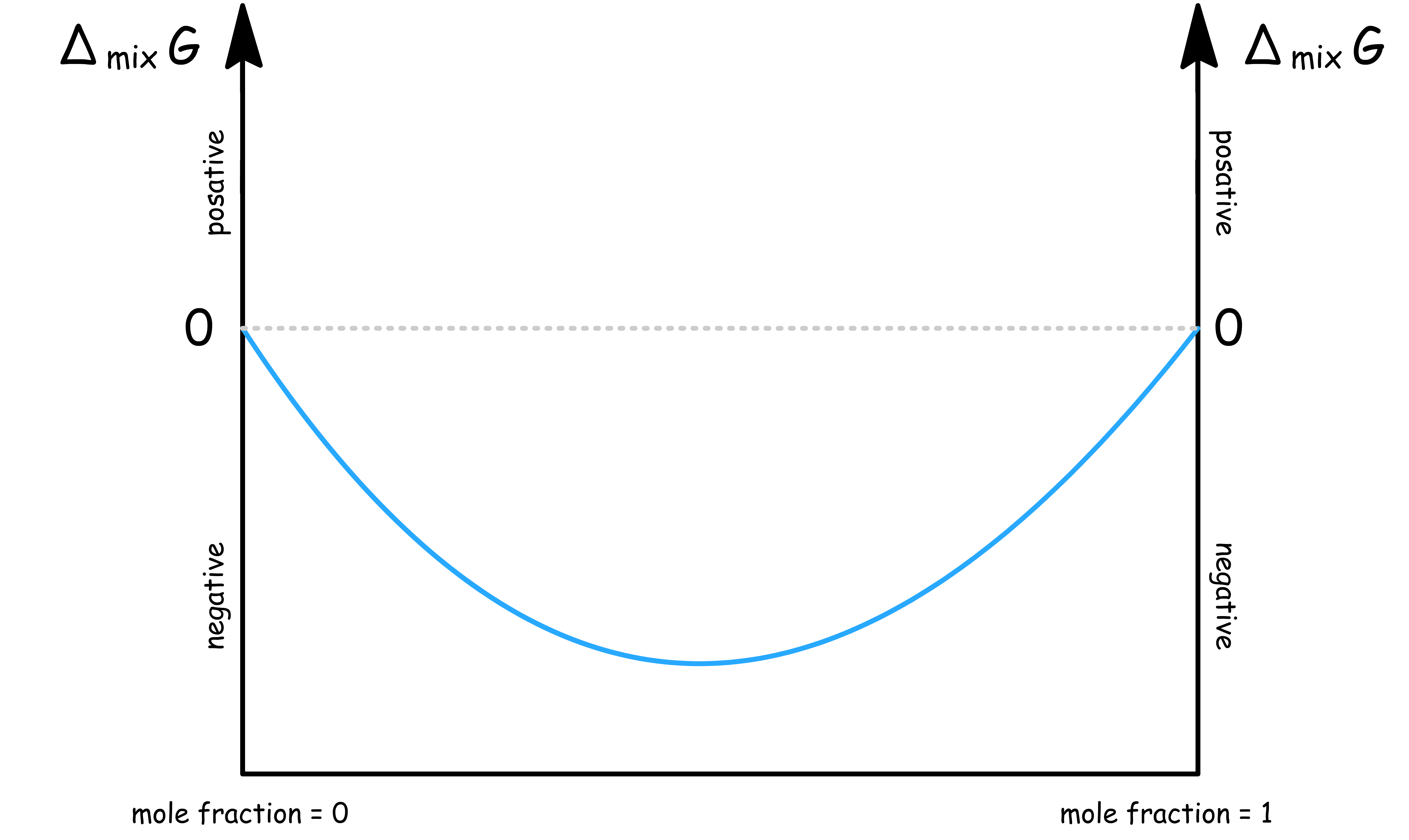
ΔmixH = 0 ( Ideal Mixing )
When the intermolecular attractions within the mixture is the same as that of the pure substances,
- In this case, is just
- For a binary system, the graph of against mole fraction is
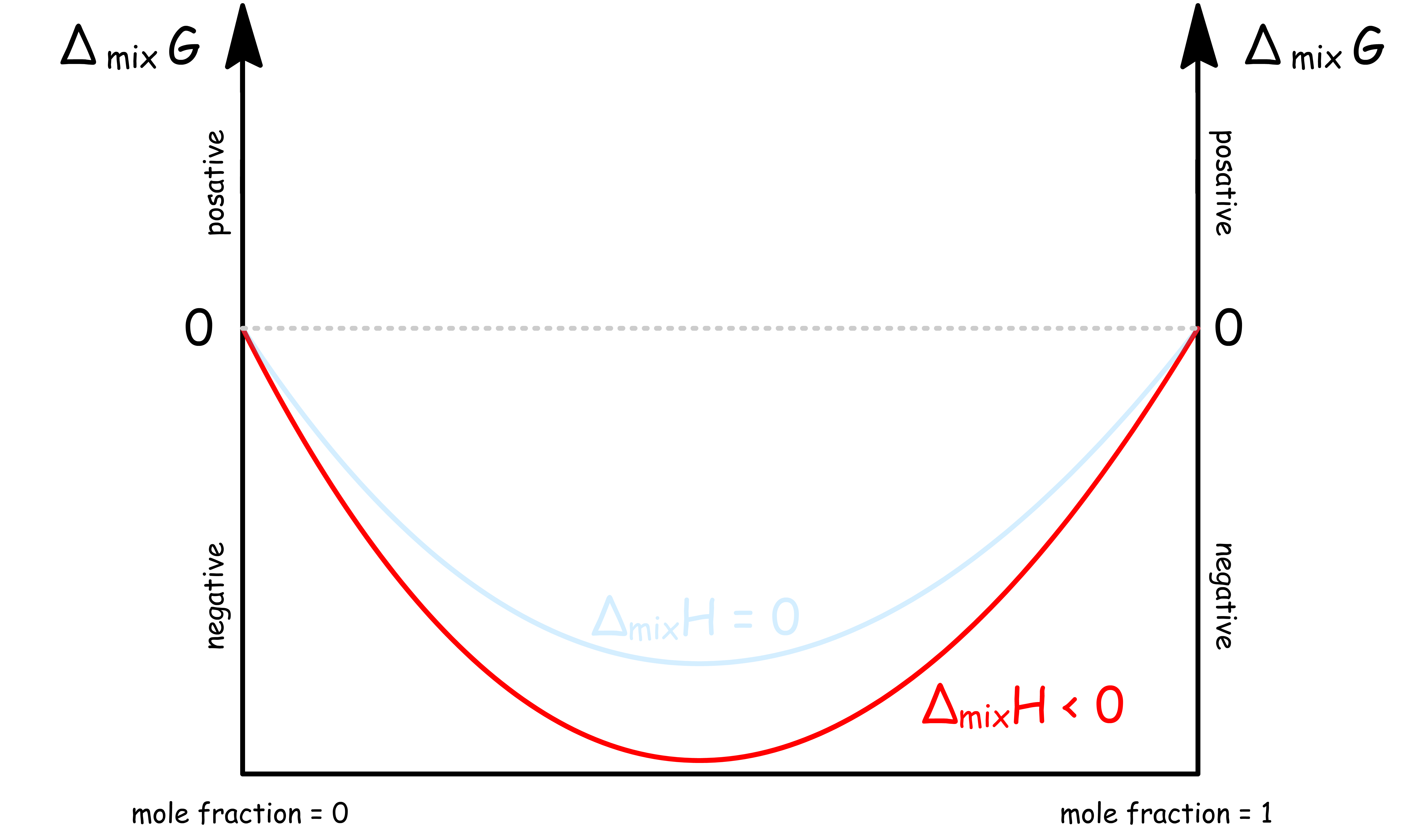
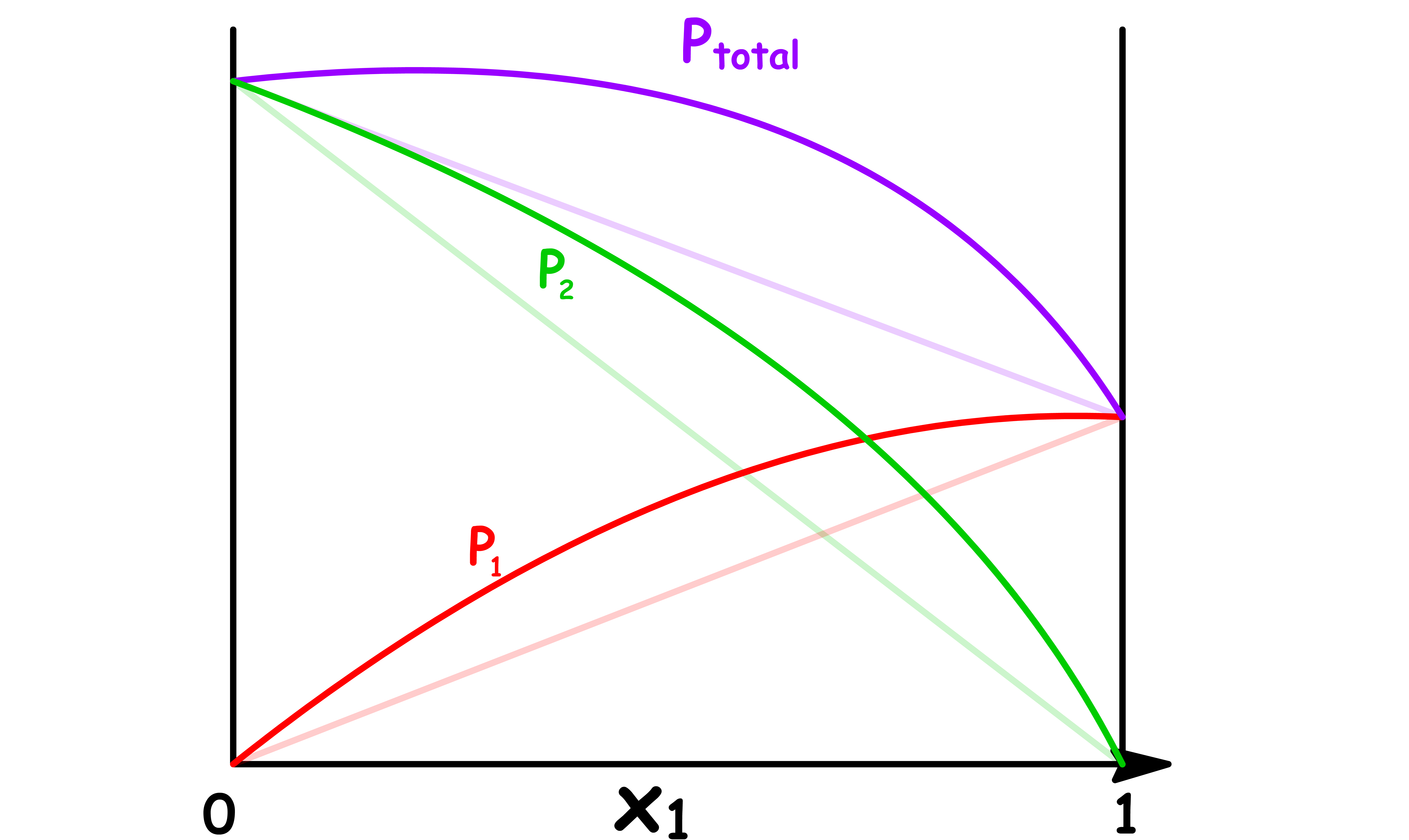
ΔmixH < 0
When the intermolecular attractions within the mixture is stronger than that of the pure substances,
- In this case, is more negative than
- For a binary system, the graph of against mole fraction is
- In other words, it is both entropically and enthalpically favorable to form the mixture
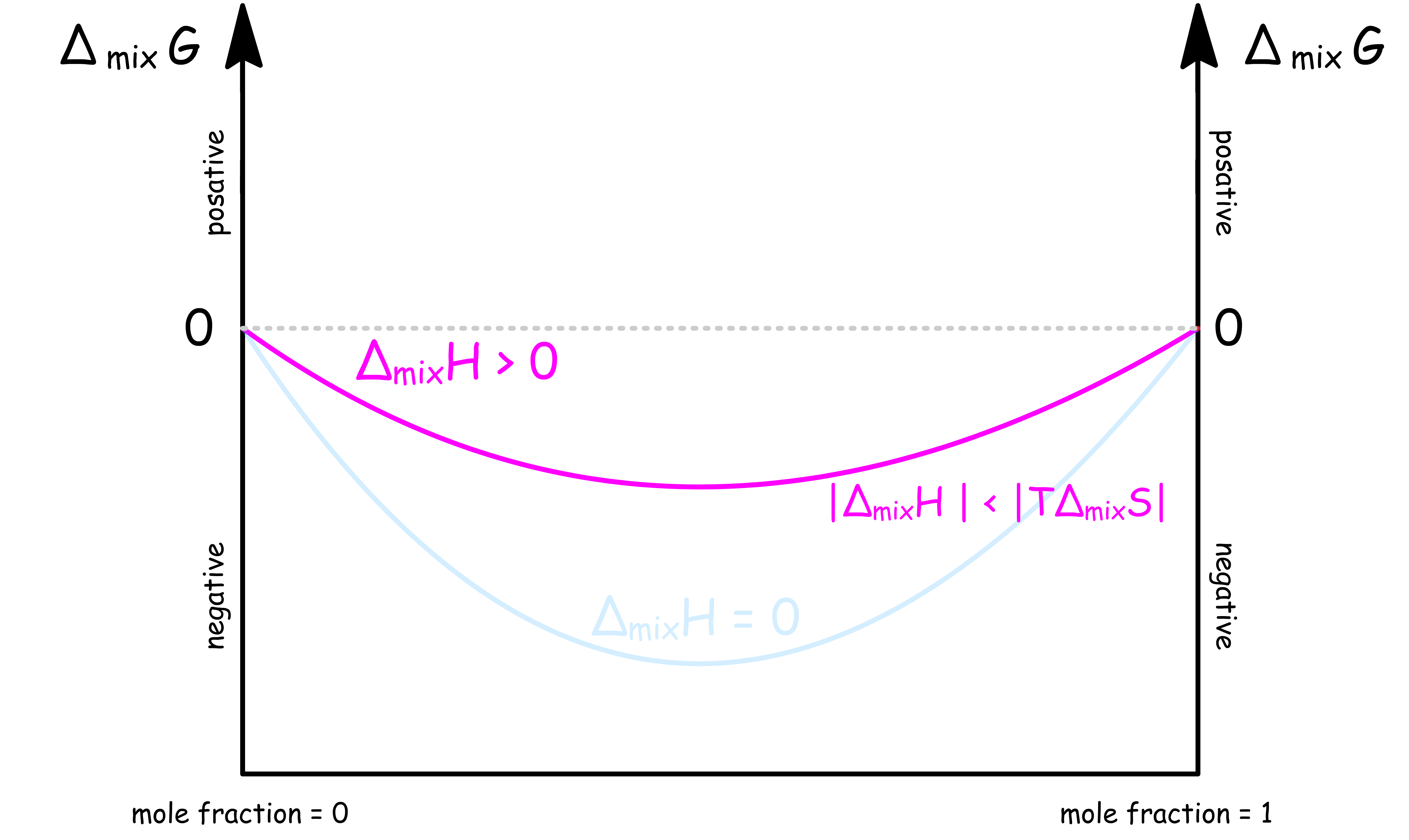
ΔmixH < 0 ; |ΔmixH| < |TΔmixS|
When the intermolecular attractions within the mixture is slightly weaker than that of the pure substances, , but the magnitude of is smaller than that of
- In this case, is less negative than
- For a binary system, the graph of against mole fraction is
- In other words, it is entropically favorable, but enthalpically unfavorable to form the mixture. However, the effect of entropy overpowers that of enthalpy, so mixing is still spontaneous
ΔmixH < 0 ; |ΔmixH| > |TΔmixS|
- When the intermolecular attractions within the mixture is a lot weaker than that of the pure substances, , but the magnitude of is greater than that of
- In this case, is less negative than
- For a binary system, the graph of against mole fraction is
- In other words, it is entropically favorable, but enthalpically unfavorable to form the mixture. However, the effect of enthalpy overpowers that of etropy, so mixing is still not spontaneous
Mixing is only spontaneous at low portions
- When either component has a small mole fraction, the is still negative, so the solution is miscible at small proportions
- Moreover, even when the solution is separated into two phases, each phase is not a pure liquid. This is because a small portion of the other component is mixed into their phase
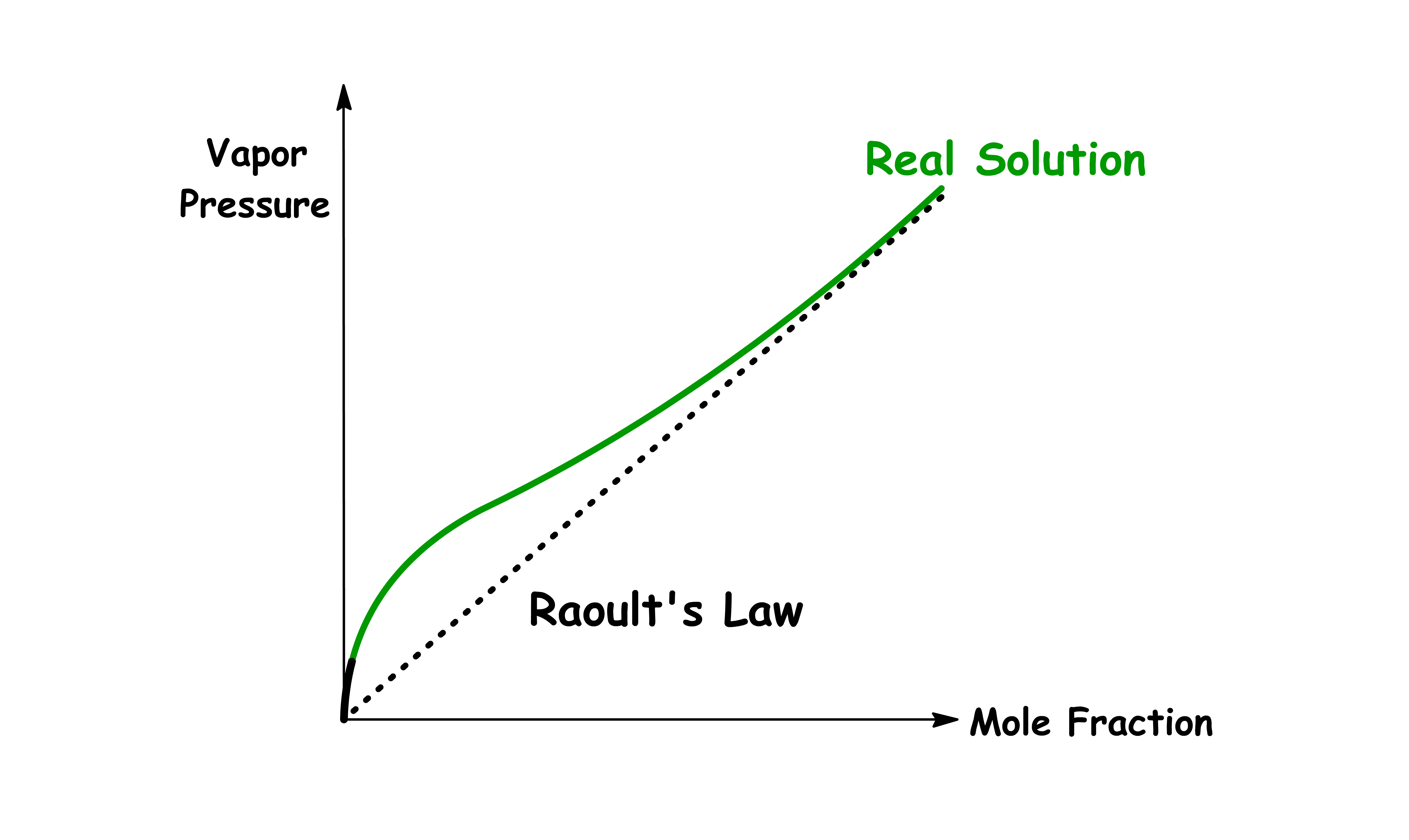
¶ Non-Ideal Solutions and Vapour Pressure
Ideal solutions are those that follows Raoult's Law, so we can define non-ideal solutions as those that don't
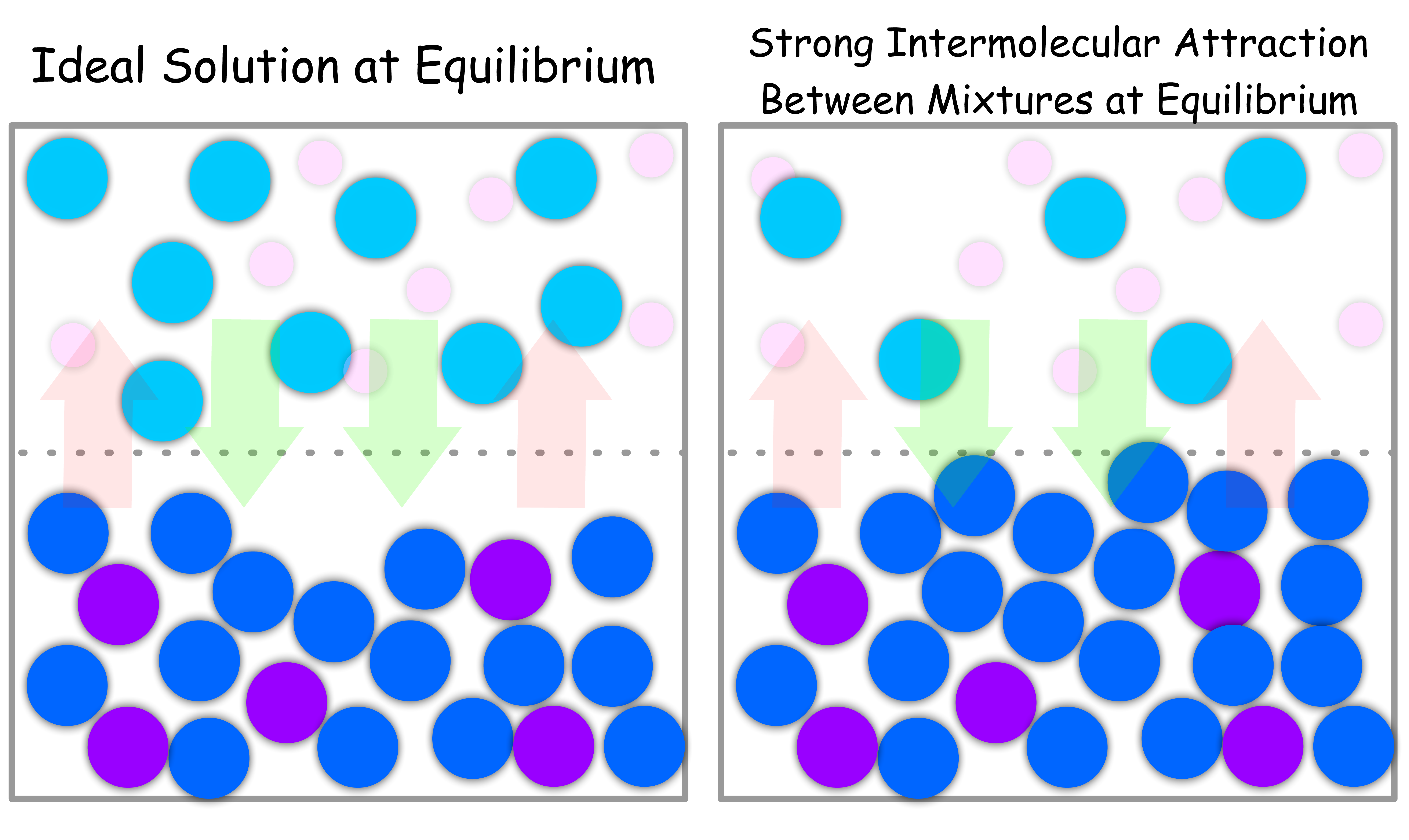
When the Intermolecular Interactions between Mixture is STRONGER than that of Pure Liquid
- Due to the stronger attraction, the molecules will prefer to stay in the condensed phase
- Since there is less vapour, the vapour pressure of each component will be lower than usual
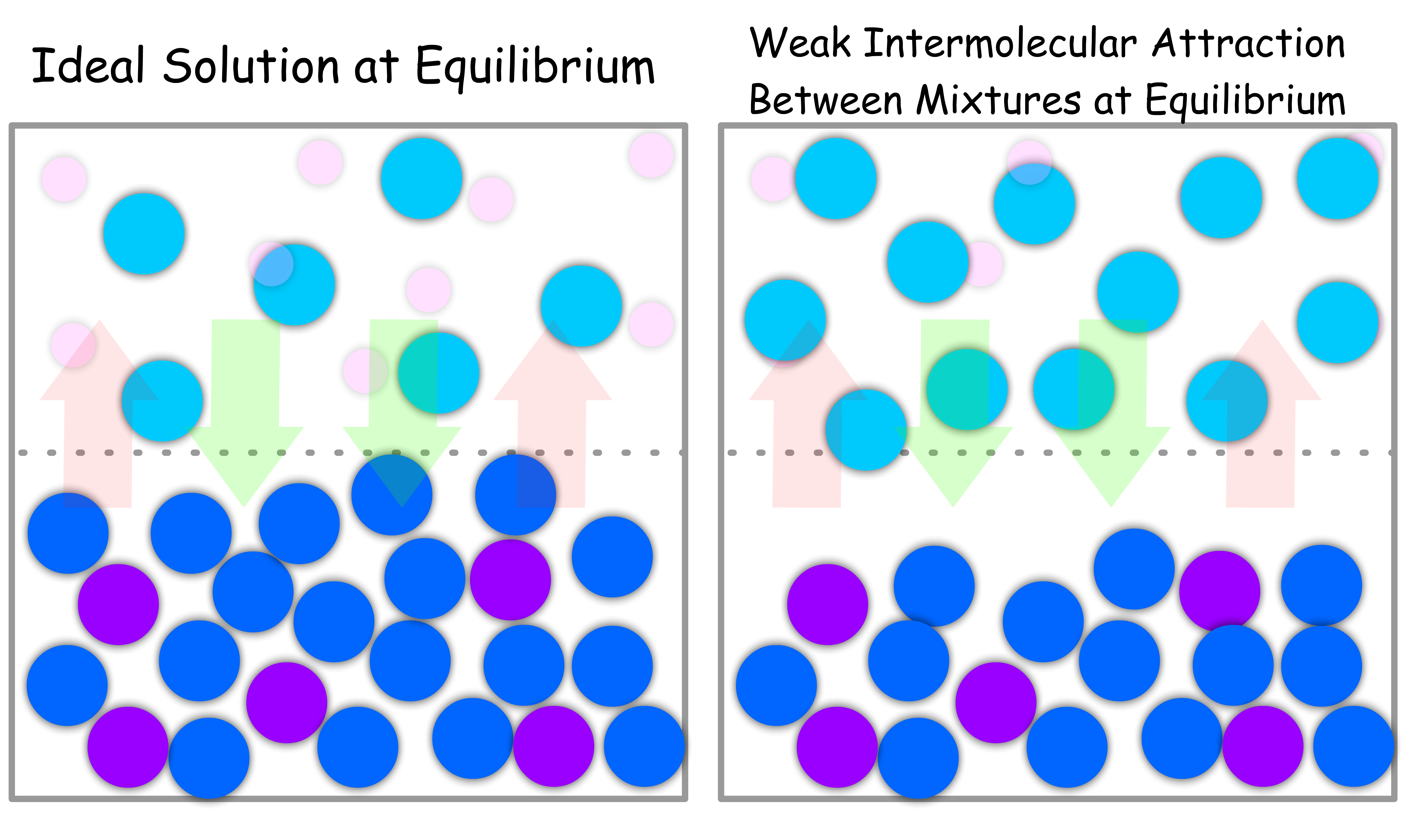
When the Intermolecular Interactions between Mixture is WEAKER than that of Pure Liquid
- Due to the weaker attraction, the molecules will have a smaller tendency to stay in the condensed phase
- Since there is more vapour, the vapour pressure of each component will be higher than usual
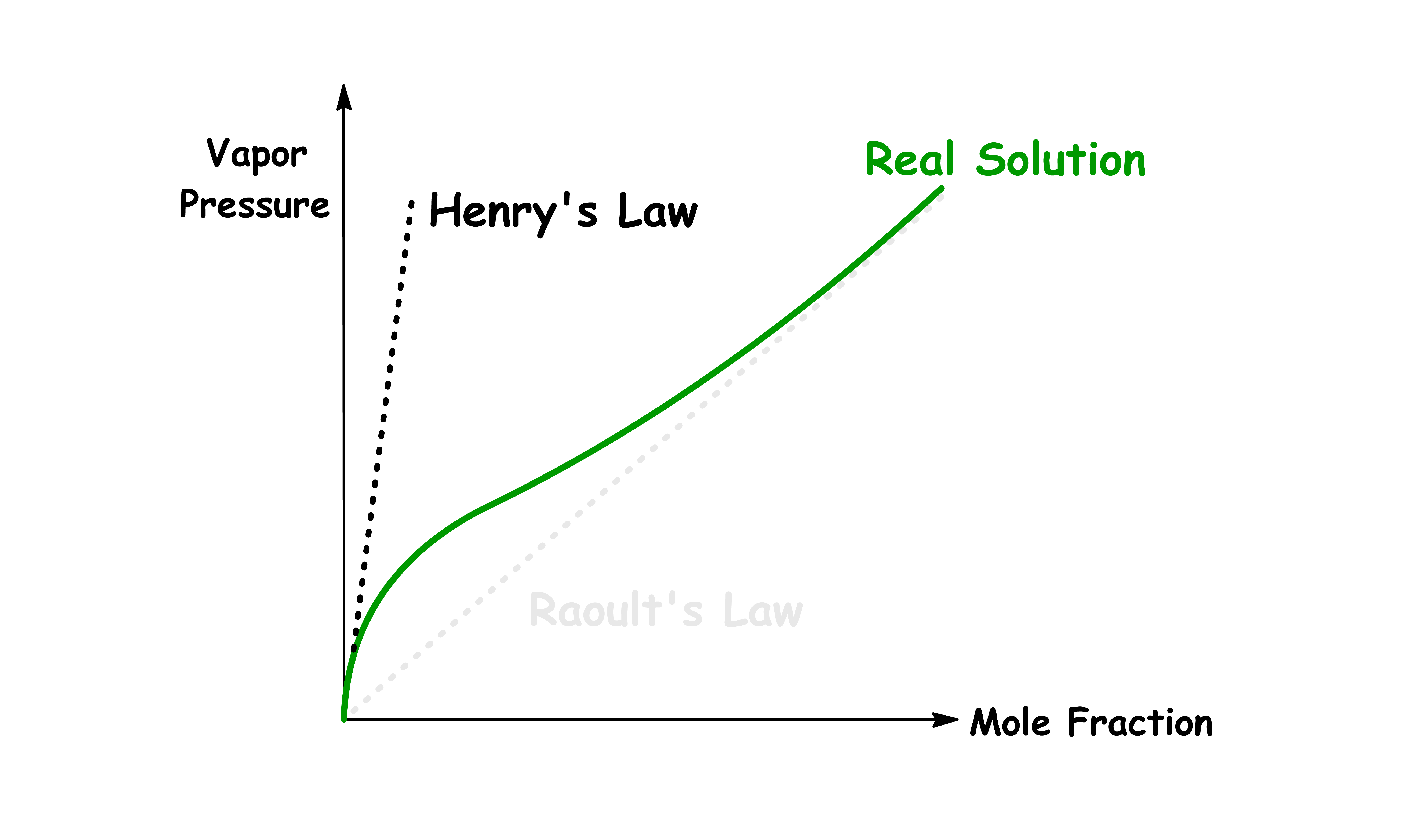
¶ Dilute Solution and Henry's Law
We often have to deal with real solutions which deviates from Raoult's law when the concentration is low
- Raoult's law is a good approximation when the concentration of the solution is high
For real solutions at low concentration, although the vapour pressure of the solute is still proportional to the mole fraction, the proportionality constant is no longer the vapour pressure of the pure substance
- The proportionality constant for dilute solution is defined as the Henry's constant, , such that
Solutions for which the solute obeys Henry's Law and the solvent obeys Raoult's Law are called ideal-dilute solutions
- The difference in behaviour of the solute and solvent at low concentration arises from the fact that in a dilute solution the solvent molecules are in an enviornment that resembles the one they have in pure liquid
- In contrast, the solute molecules are surrounded by solvent molecules, which is entirely different from their environment when pure
¶ Colligative Properties
Colligative properties are properties of liquid solutions which depend mainly on the number rather than the nature of solute molecules present
We make two assumptions when discussing these colligative properties
The solute is non-volatile and does not contribute to the vapour
The solute separates out from the solvent when the solvent is frozen
The origin of these colligative properties is that the chemical potential of solution is lower than that of pure liquids
¶ Depression of Melting Point and Elevation of Boiling Point
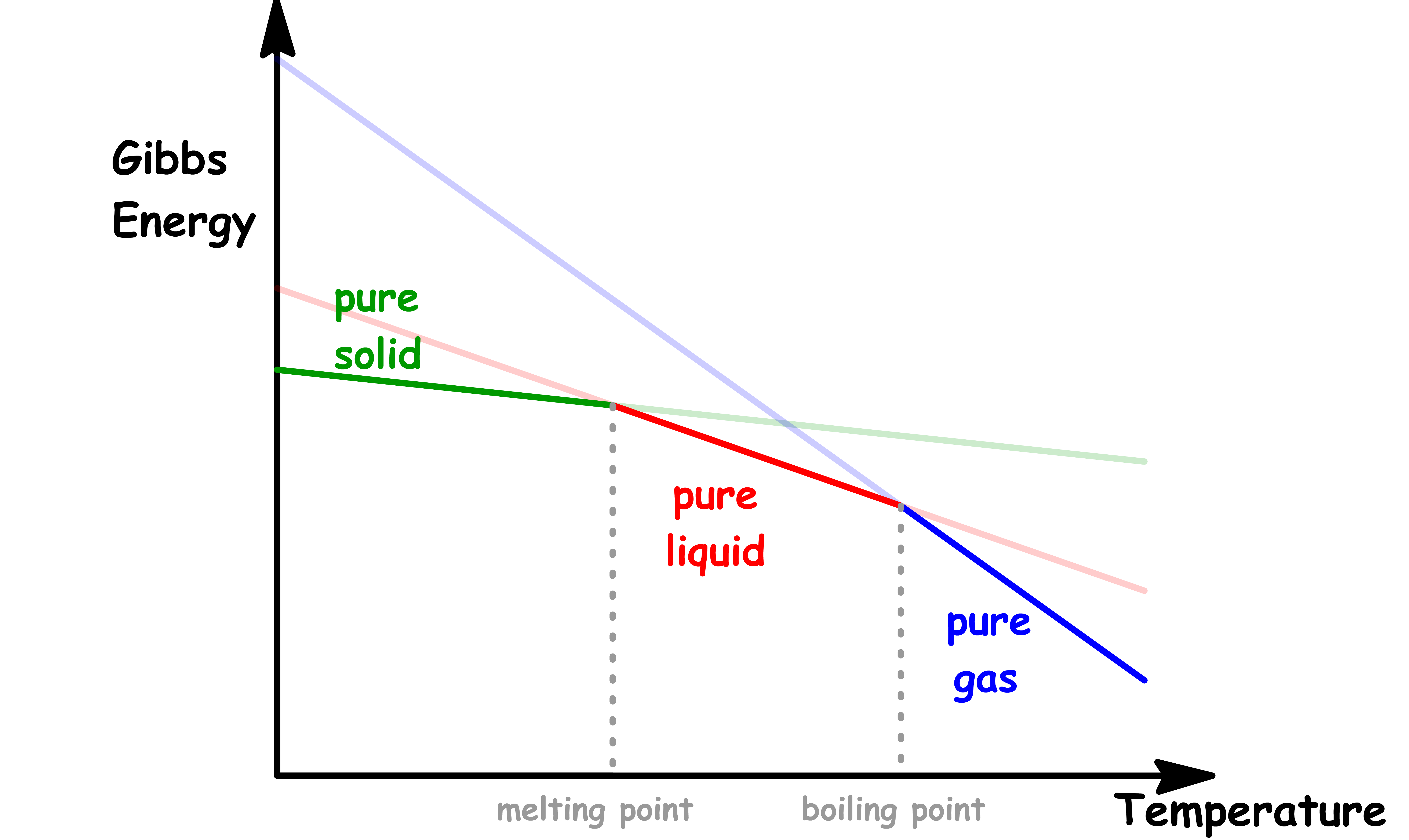
At any given external pressure, we can determine which phase is the most stable by studying the temperature-dependence of Gibbs energya
- The point of interscetions are the melting point and boiling points
From the Fundamental Thermodynamic Relations, we know that the slope of each phase is given by the negative entropy of said phase
- A mixture has a higher entropy than pure liquid, so the slope will be steeper
- Assuming it is an ideal solution, the enthalpy, and hence the y-intercept, should stay the same
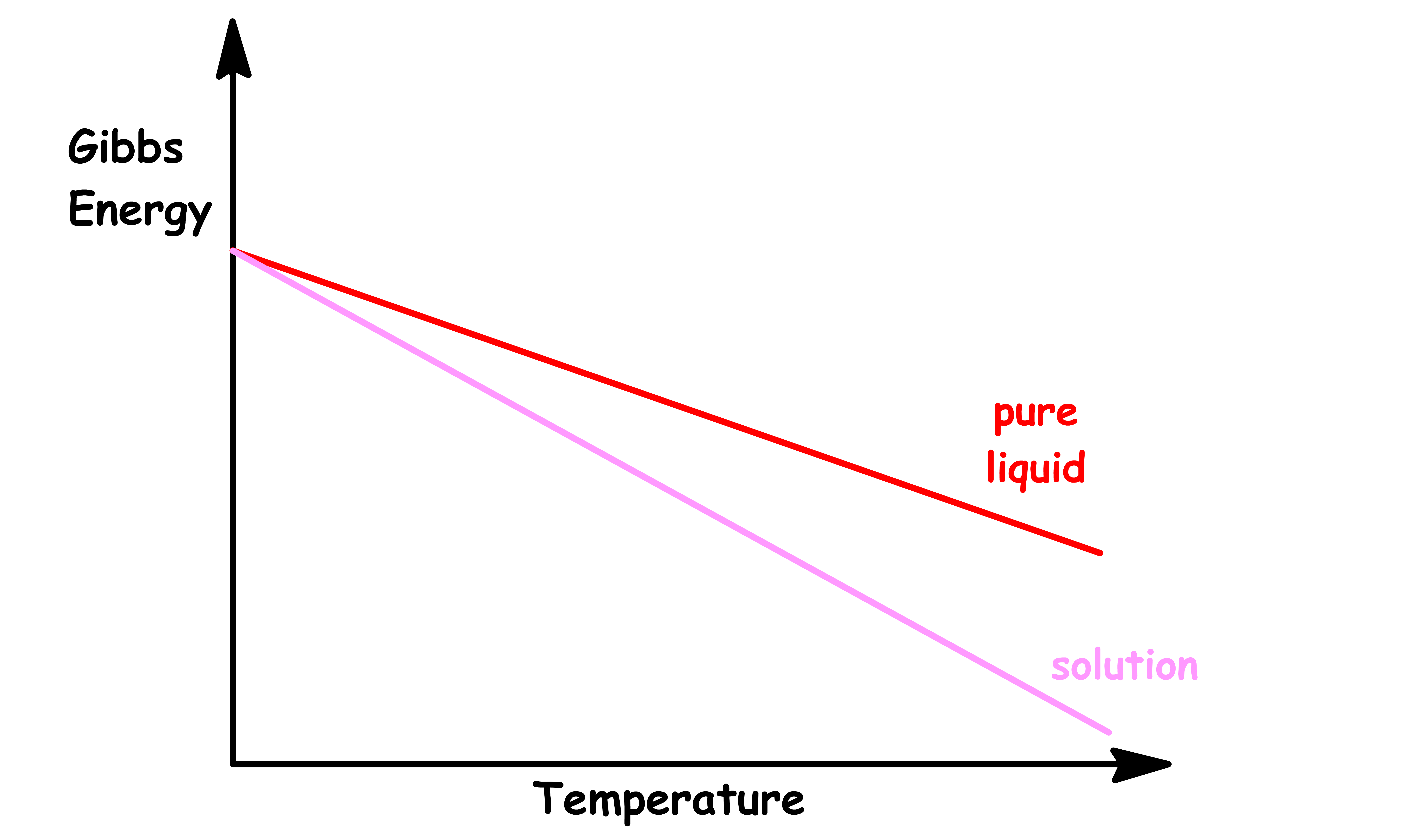
If we return to the original diagram, we will see that the melting point is lowered and the boiling point is raised
- When a solute is present, there is an additional contribution to entropy of the liquid, even in an ideal solution
- Because the entropy of the solution is already higher than that of the pure liquid, it is less entropically favorable to form a gas
- Similarly, enhanced molecular randomness of the solution opposes the tendency to freeze
¶ Osmosis
Consider the following situation
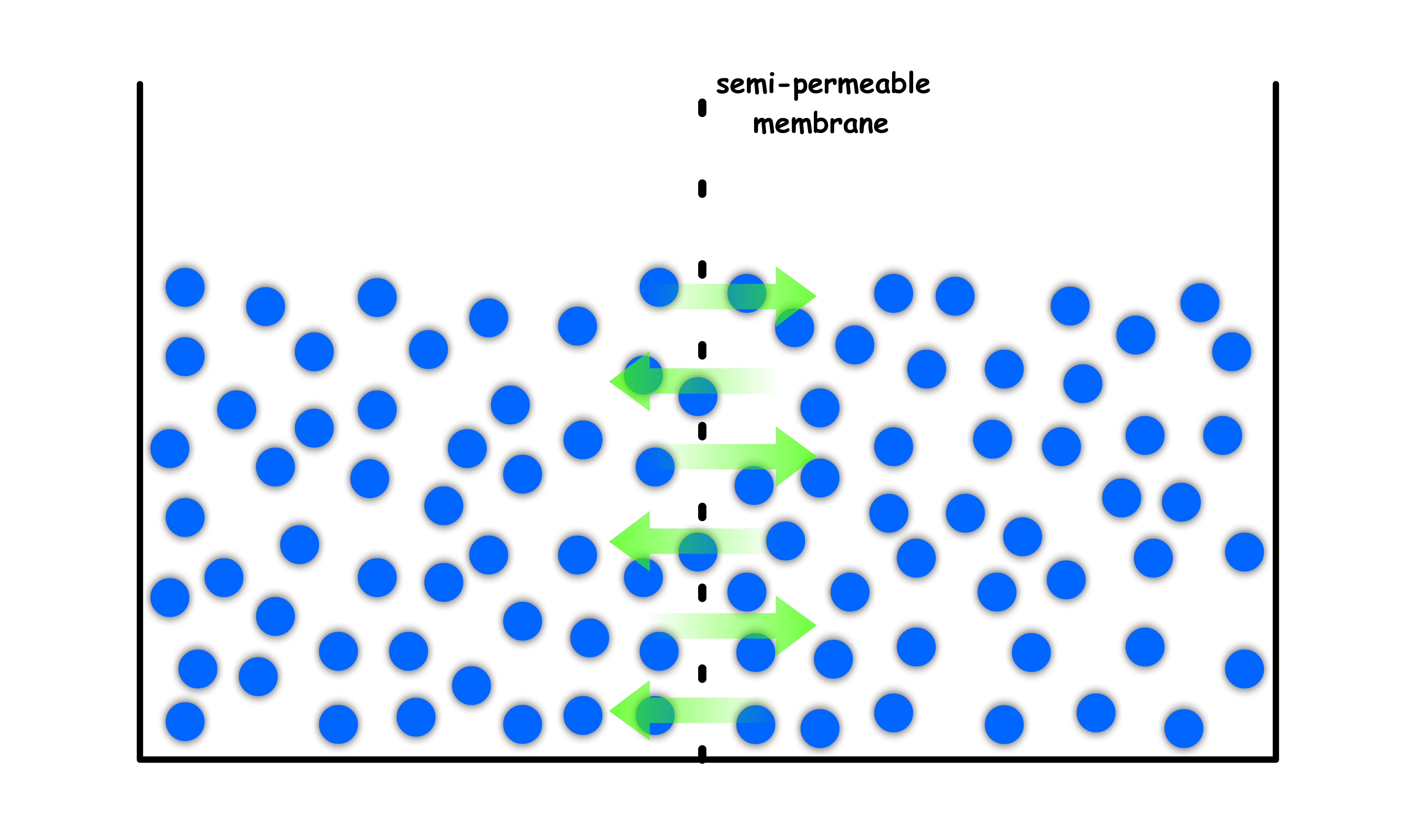
Initially, we have a container of pure liquid that is separated into two compartments by a semi-permeable membrane
- The liquid is free to pass through the membrane
- Due to having the same composition, the chemical potential of both compartments are the same. Hence, the system is in equilibrium
- At equilibrium, the level of the liquid should be the same since the rate of molecules leaving to other side is matched by the rate of molecules returning from the other side
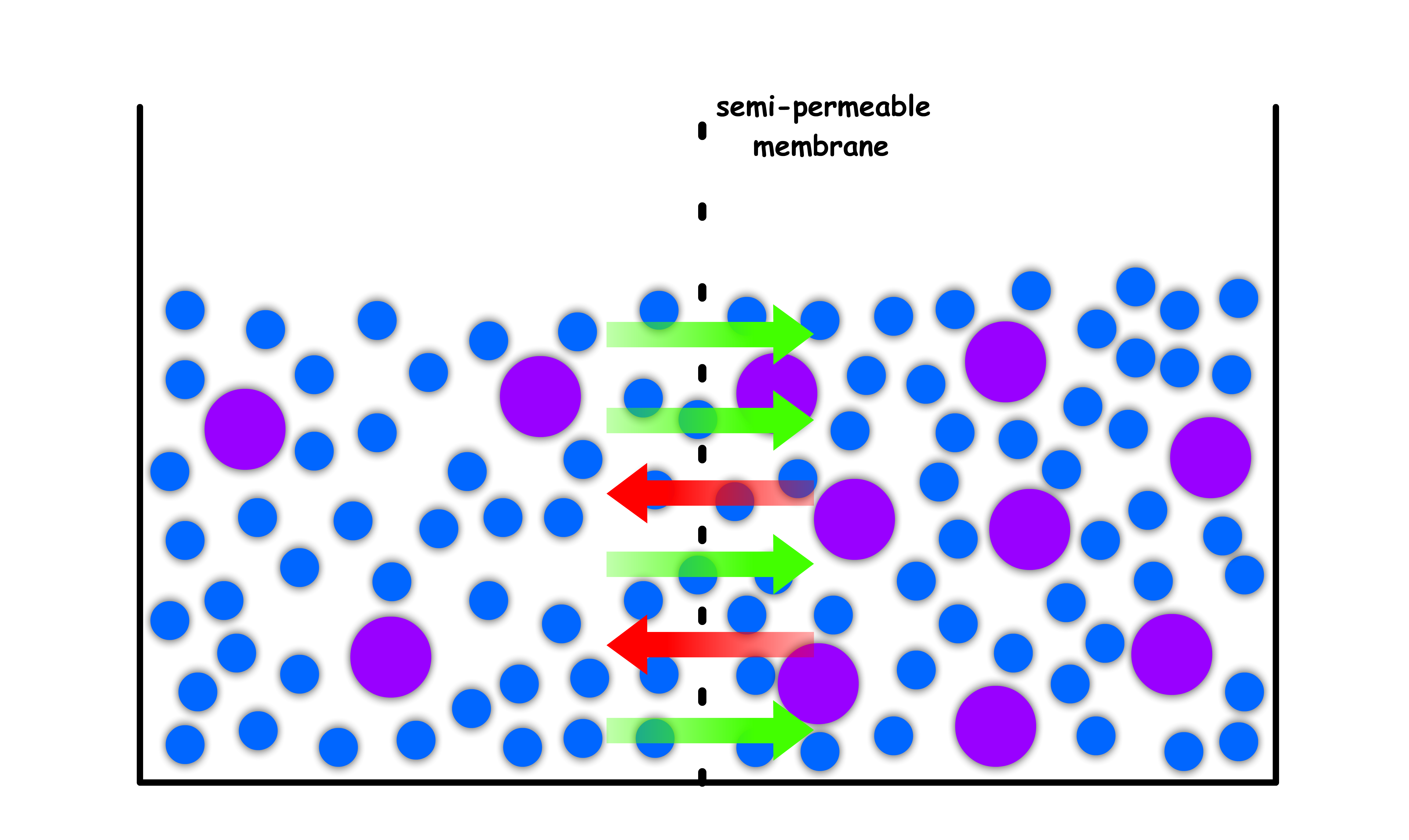
We then add some solute to both of the compartments, but make sure one side is more concentrated than the other
- The membrane is impermeable to the solute
- The moment we introduce the solute, the equilibrium is disrupted as the chemical potential in the two compartments are no longer equal
- As established before, the chemical potential of a concentrated solution is lower than that of a dilute solution ( think about chemical potential of pure liquid vs chemical potential of solution )
- The difference in chemical potential means that there will be a net flow of solvent molecules from the dilute side to the concentrated side
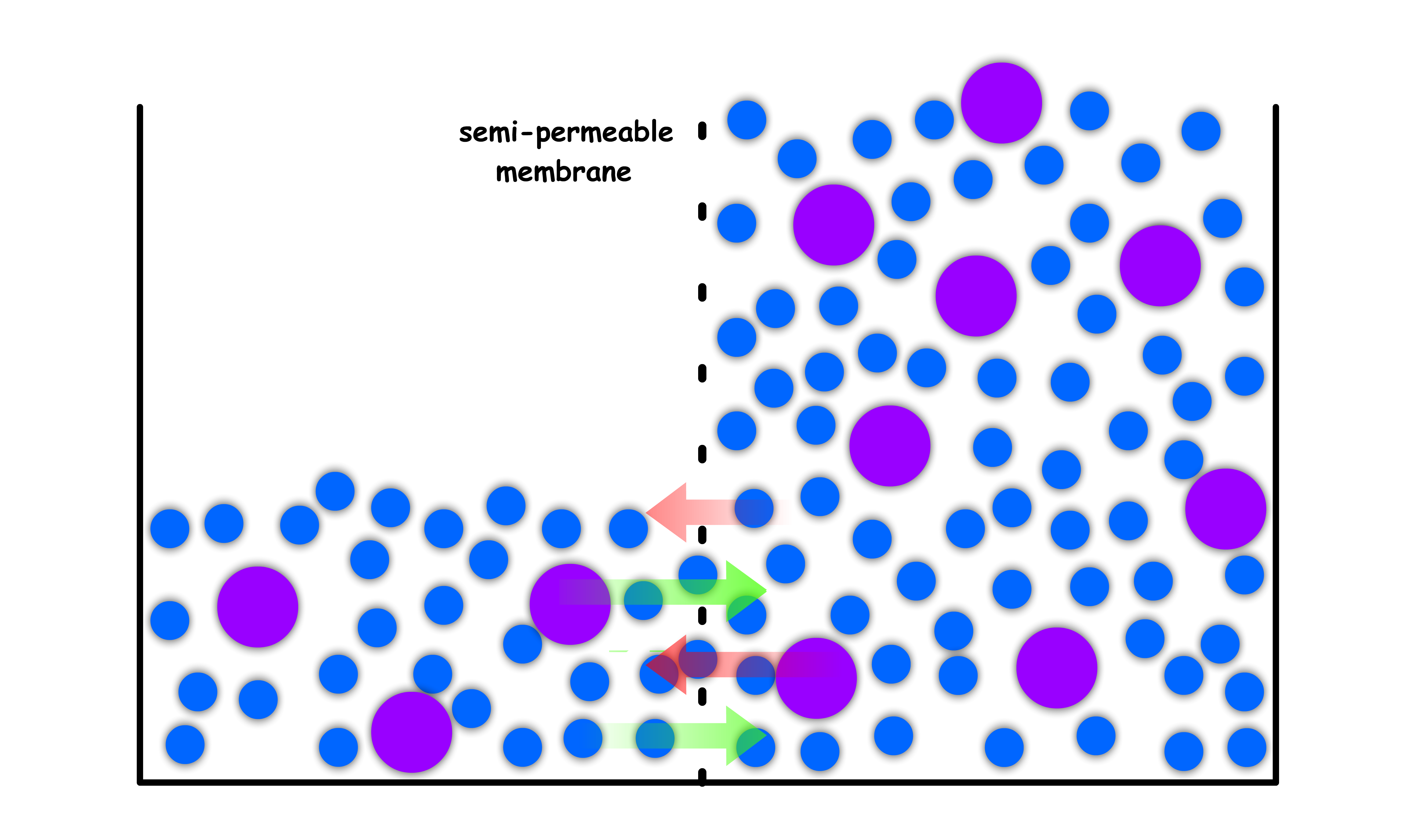
A new equilibrium will be established when the concentration of both compartments are the same
- When the solvent molecules leave the dilute solution to the concentrated solution, it accomplishes two things
- It causes the concetration of the dilute solution to increase
- It causes the concetration of the concentrated solution to decrease
- As a result, the chemical potential of the dilute solution will decrease while the chemical potential of the concentrated solution will increase. Once the chemical potential of both sides are the same, there won't be any net movement of solvent molecules
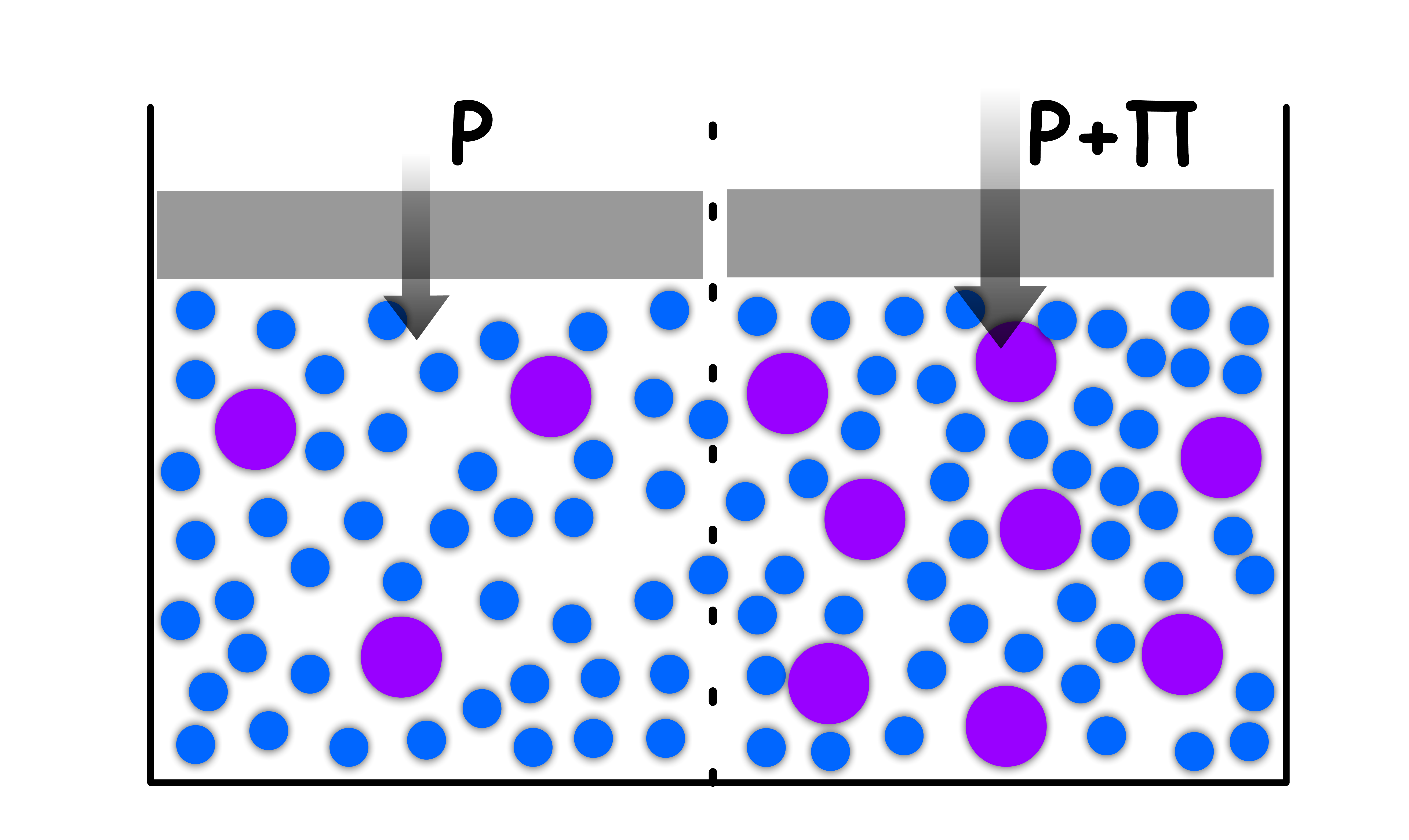
Osmotic Pressure,
- The phenomenon of osmosis is the spontaneous passage of solvent into a solution separated from it by a semi-permeable membrane
- The osmotic pressure, , is the external pressure that must be exerted to the more concentrated solution in order to stop the influx of solvent
- The osmotic pressure is given by the van't Hoff equation