Equilibria is extremely important in thermodynamics
- One special type of equilibrium that we chemists are particularly interested in is chemical equilibria
Chemical equilibria are processes where the forward and backward reactions are occurring simultaneously at just the same rate so that there is no overall change in the chemical composition of the system
- This is called a dynamic equilibrium. That is, things are constantly moving, but they are going nowhere
- Usually, equilibrium happens when the internal or external pressure are balanced, or when there's no temperature gradient between the system and the surrounding. However, chemical equilibria are particularly concerned with the "balance of the composition within the system"
¶ Thermodynamic Potentials and Equilibrium
In previous section, we have established the relationship between the thermodynamic potentials and equilibrium
- All thermodynamic potentials ( , , , ) can be used to indicate the direction of a process when both of their natural variables are set to constant
- is a thermodynamic potential and and are its convenient natural variables
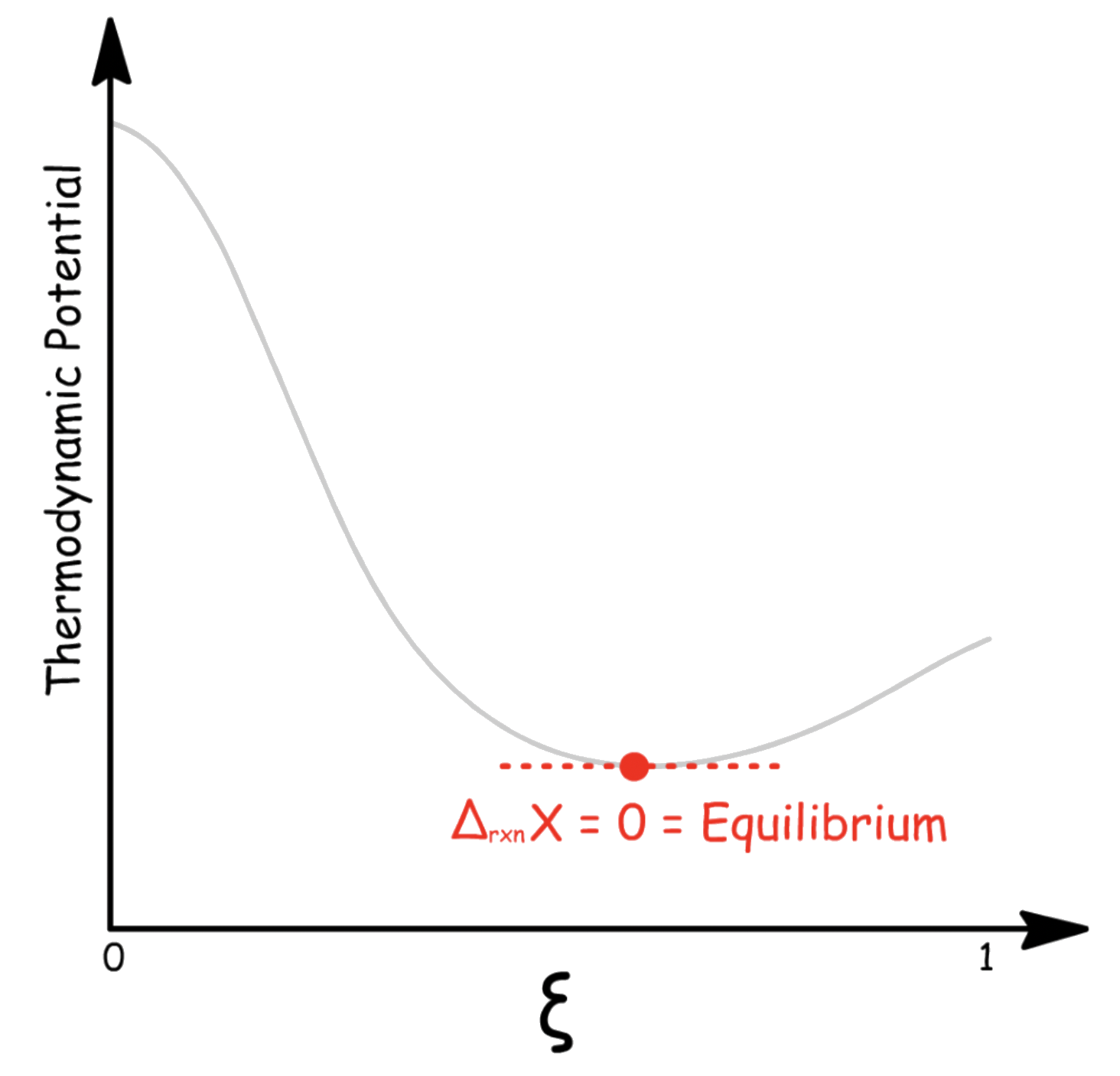
- Equilibrium is established when the thermodynamic potential of the system is at its minimum with both its natural variable set to constant
We also know that the rate of change of a thermodynamic potential with respect to the mole number of a component is the chemical potential when both its natural variable are set to constant
- This relationship will prove to be important when discussing chemical equilibrium
¶ The Extent of a Reaction
When both the convenient natural variables are held constant, the change in thermodynamic potential is the sum of chemical potential multiplied by the change in mole number of each component
Suppose a reaction occurs and the composition of the system changes, such that an infinitesimal amount ( ) of reactant is converted to product
- The change in mole number of each component that is involved in the reaction is
- is the stochiometric coefficient of the ith component in the balanced equation
- is positive for products, negative for reactants
With this expression of dni, we can obtain a new expression for the change in the thermodynamic potential
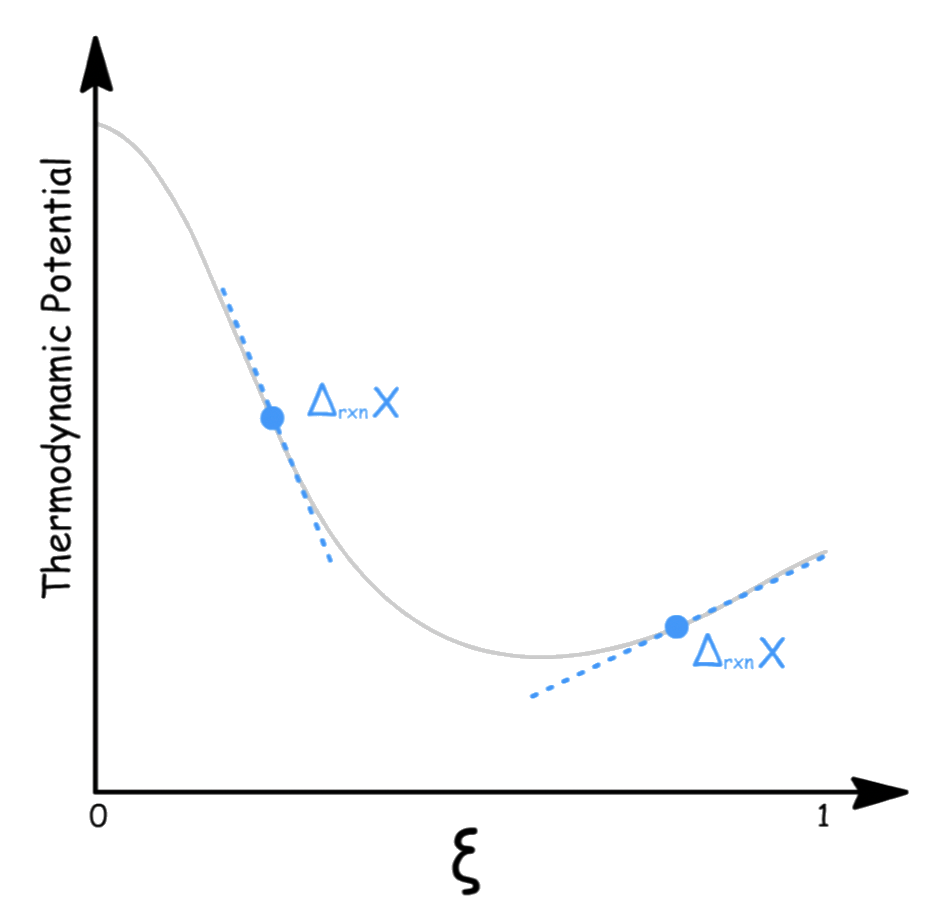
is called the extent of reaction, it is a measure of the progress of a reaction
- is equal to when the reaction position lies completely on the reactant side and is equal to when the reaction position lies completely on the product side
- The possible numerical values of may vary depending on the initial conditions and the reaction stoichiometry
- The value of changes with time, but every component in the system at a given time will have the same value of
We are now in a position where we can define a new quantity that can help us determine the point of equilibrium
- Using the equation we just proved, we can derive a new equation that describes the rate of change of the thermodynamic potential with respect to the extent of reaction
- We define a new notation, to denote the partial derivative
Although Δ usually signifies a difference in values, here it signifies a derivative, the rate of change of the thermodynamic potential with respect to the extent of the reaction
- A little bit of rearrangement will give us
- Equilibrium is established when , which is only possible when
- Therefore, is the condition for equilibrium
We can also interpret as the difference between the chemical potentials of the reactant and products at the certain composition of the reaction mixture
- We have derived two ways to express dX_
- Simply by inspection, we can say
- We know that is positive for products and negative for reactants, so we can express it as
We can therefore determine the spontaneity using the chemical potentials
- When the sum of the chemical potential of the reactants is greater than that of the products, the forward reaction is spontaneous
- When the sum of the chemical potential of the reactants is greater than that of the products, the forward reaction is nonspontaneous ( Backward reaction is spontaneous )
- When the sum of the chemical potential of the reactants is equal to the sum of the chemical potential of the products, the system is in equilibrium
¶ Reaction Quotient and Equilibrium Constant
¶ Gibbs Energy is the Favorite Child
Although we can use any of the four thermodynamic potentials to describe equilibrium, we choose to use Gibbs energy more often than the others
- This is because the natural variables of Gibbs energy is pressure and temperature. Setting those two variables to constant can be easily achieved even in a regular laboratory
- There is absolutely nothing special about Gibbs energy in this context
When we are using Gibbs energy to describe equilibrium, we call the reaction Gibbs energy
- It has the exact same property as as described before
Before we go another further, it is important to understand the relation between Gibbs energy and pressure
- From the fundamental thermodynamic relations we know that
- We can perform some rearrangements to get
- Assuming ideal gas behavior, we can substitute out
- If we integrate this expression, we will get
- If we set the initial state to the standard state (), and the final state to the state that we are interested in, we will get
- The pressure of the standard state is just 1 atm, so we can just omit it
- Owing to the relationship between Gibbs energy and chemical potential, we can write a similar expression ( without n and the pressure becomes partial pressure ) for chemical potential of a component
¶ Reaction Quotient
Although we can easily use Gibbs energy ( or any other thermodynamic potentials ) to determine the extent of reaction, it is hardly convenient
- It is more convenient to determine the extent of reaction using the relative amount of components within the system
We can derive this new quantity using reaction Gibbs energy
- By definition, at constant pressure and temperature, the reaction Gibbs energy can be expressed as the sum of the product of chemical potential and the stochiometric coefficient
- We can substitute the chemical potential for the expression that relates pressure to chemical potential
- After simplifying the expression, we will get
- Using some basic logarithmic properties, we can rearrange the equation
- The sum of logarithmic terms is natural log of the product of these terms
We shall define the quantity within the natural log as the reaction quotient
- The reaction quotient measures the relative amounts of products and reactants present during a reaction at a particular point in time
- Since the composition of the system is changing, so the value of the reaction quotient will also change as the reaction progresses
If we substitute the reaction quotient back to the original equation, we will get
- The value of depends on the exact conditions of the system and the extent of the reaction
- is the difference in Gibbs energy between products and reactants when all components in the system are in their standard states of pressure, form and concentration. We can therefore see it as is a constant whose value is a characteristic of the reaction
¶ Equilibrium Constant
The reaction quotient measures the relative amounts of products and reactants present at a certain point during the reaction
- We should also define a quantity that is used to measure specifically the relative amount of products and reactants at equilibrium
We can define the value of the reaction quotient at equilibrium as a new constant, the equilibrium constant ( K )
- The equilibrium constant is some quantity which characterizes the equilibrium position in terms of the amounts of materials present in the equilibrium mixture
We are now at a position to devise an expression for systems at equilibrium
- At equilibrium, the reaction Gibbs energy is zero and the reaction quotient can be replaced by equilibrium constant
- Rearranging the expression will give us the relation
¶ Significance of Reaction Quotient and Equilibrium Constant
K is defined in terms of the relative amount of products and reactants at equilibrium
- When the value of K is large, it means the equilibrium position lies to the product side
- When the value of K is small, it means the equilibrium position lies to the reactant side
Since the value of the reaction quotient is always tending towards the value of the equilibrium constant, by comparing the relative value of the reaction quotient and the equilibrium constant, we will know the direction of the equilibrium at any given point in the reaction
- If Q = K, then the system is already at equilibrium, and no further change in the composition of the system will occur unless the conditions are changed
- If Q < K, the reaction will proceed to the right as written, forming products at the expense of reactants
- If Q > K, the reaction will proceed to the left as written, forming reactants at the expense of products
The equation that relates the standard reaction Gibbs energy to the equilibrium constant allow us to determine the extent of the reaction at equilibrium
- If is positive, then the value of the equilibrium constant must be between 0 and 1, which means the equilibrium position lies closer to the reactant side
- If is negative, then the value of the equilibrium constant must be greater than 1, which means the equilibrium position lies closer to the product side
We know that we can determine the spontaneity of a process at any stage by looking at the sign of the reaction Gibbs energy
- Using the equation that relates the reaction Gibbs energy and the reaction quotient, we can determine each other's sign or relative value
A common misconception is that a reaction is spontaneous if . However, this is untrue. Whether or not a reaction is spontaneous at a particular composition depends on the value of , but not
- determines the direction ( or spontaneity ) of a reaction at a particular point in time
- determines the position of the equilibrium at the equilibrium position