Many equations we have derived and use thus far can only be applied to situations with certain restrictions
- The restrictions is usually done by setting a certain variable constant
- This limitation means that we have been dealing with the special case
We need to find a set of equations that can be applicable in most, if not all cases
- These set of equations do not require any restrictions to work
- We call these set of equations, the fundamental thermodynamic relations
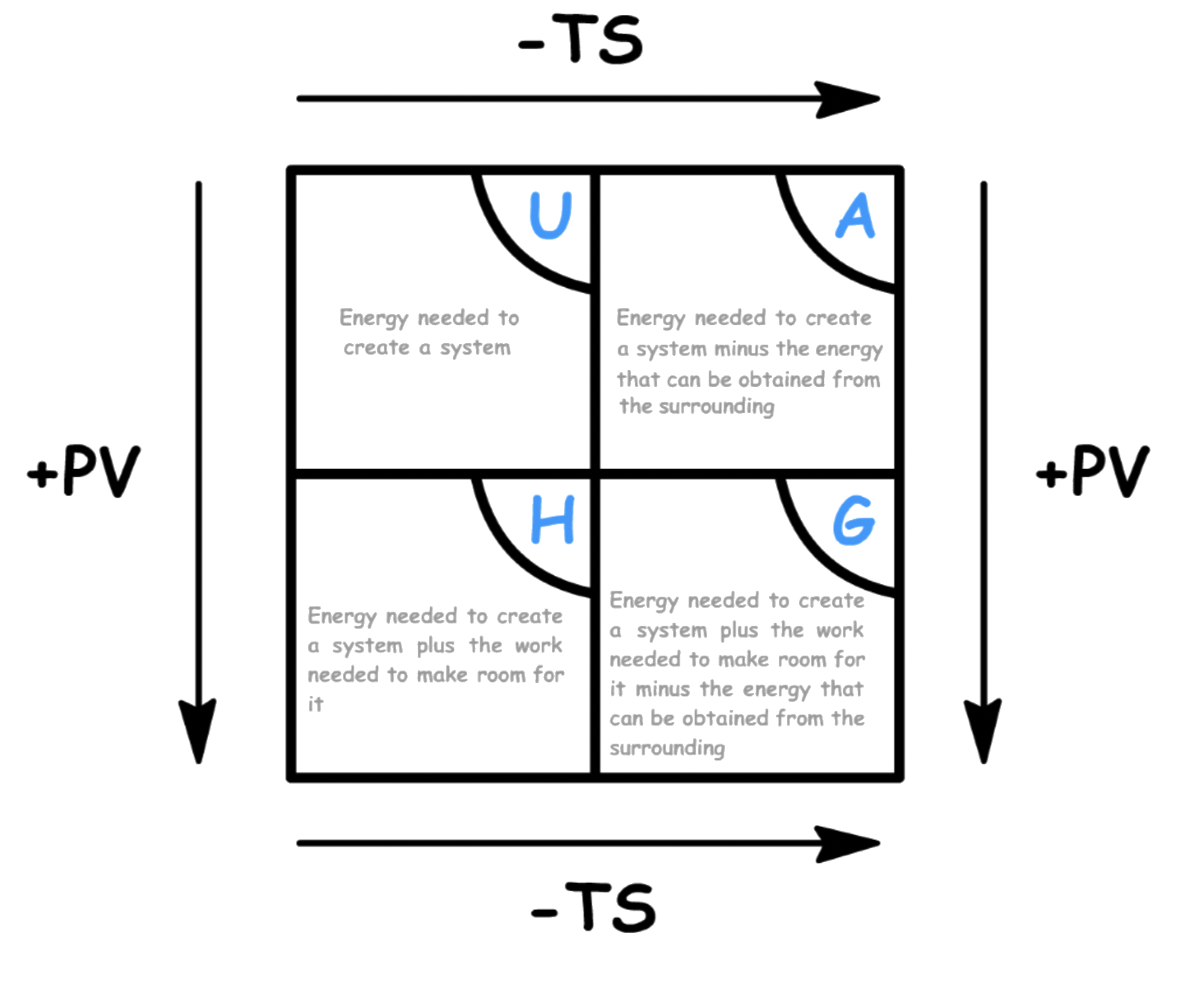
The fundamental thermodynamic relation are four fundamental equations which demonstrate how four important thermodynamic quantities depend on variables that can be controlled and measured experimentally
- These four thermodynamic quantities are Internal Energy ( ), Enthalpy ( ), Helmholtz Energy ( ) and Gibbs Energy ( )
- Collectively, these four thermodynamic quantities are called the thermodynamic potential
-These equations involve only functions of state, so it is true for all changes, not just reversible ones
The fundamental thermodynamic equations follow from five primary thermodynamic definitions and describe the thermodynamic potentials in terms of their natural variables
- Natural variables refer to state functions like: Pressure, Volume, Temperature and Entropy
- We are defining state functions that are describing energy ( , , and ) with state functions that are not describing energy ( , , , )
- These equations are important because when the behaviors of these energies on their natural variable are known, all thermodynamic properties of the system can be determined
¶ The Thermodynamic Potentials and Natural Variables
We can define a thermodynamic potential in terms of any natural variable, since they are all interrelated
- However, in the fundamental relations, each thermodynamic potential only has two "convenient" natural variable assigned to it
- The combination of "convenient" natural variables is unique to the thermodynamic potential
¶ The Four Fundamental Thermodynamic Relations
In order to derive an equation that is generally applicable for each thermodynamic potential, we should start with each of their definition
- Through rearrangement and substitution only, we can derive a fundamental equation for each energy without imposing any restrictions
Each of the fundamental equation should have the form
- is a thermodynamic potential ( , , or ), while , , and are the natural variables ( , , , )
- and are the convenient natural variables of , while and are not
¶ Internal Energy
- By definition, the change in internal energy is the sum of heat exchange in work done
- Since the value of does not depend on path, we can set the path to a reversible one
- Assuming there is only expansion work being done, we can replace the work term
- We can also substitute the reversible heat flow in terms of entropy and temperature
- This is the fundamental equation for internal energy and we can see that volume ( ) and entropy ( ) are the natural variables of internal energy ( )
- The fundamental equation of internal energy is the cornerstone of all fundamental equations as the other fundamental equations are derived directly or indirectly from this equation
¶ Enthalpy
- By definition, enthalpy is the sum of internal energy and the product of pressure and volume
- The differential of enthalpy is therefore
- We can then substitute dU with the fundamental equation of internal energy
- We can then cancel out the pdV term
- This is the fundamental equation for enthalpy and we can see that pressure ( ) and entropy ( ) are the natural variables of enthalpy ( )
¶ Helmholtz Energy
- By definition, Helmholtz energy is the difference between internal energy and the product of entropy and temperature
- The differential of Helmholtz energy is therefore
- We can then substitute dU with the fundamental equation of internal energy
- We can then cancel out the TdS term
- This is the fundamental equation for Helmholtz free energy and we can see that volume ( ) and temperature ( ) are the natural variables of Helmholtz energy ( )
¶ Gibbs Energy
- By definition, Gibbs energy is the difference between enthalpy and the product of entropy and temperature
- The differential of Gibbs energy is therefore
- We can then substitute dU with the fundamental equation of enthalpy
- We can then cancel out the TdS term
- This is the fundamental equation for Gibbs energy and we can see that pressure ( ) and temperature ( ) are the natural variables of Gibbs energy ( )
¶ Fundamental Equations in terms of Partial Derivatives
We have established in the first chapter that a state function can be written in the form of partial differential equation of other state functions
- Both the thermodynamic potentials and the natural variables are state functions, so we can express the four fundamental equations in the form of partial differential
- is the thermodynamic potential, while and are its convenient natural variables
- We can interpret the equation as such: The change of X must be attributed to a sum of change in and , and how much and each affects X depends on the rate of change of X with respect to or
If we compare the two ways of expressing the same equation, we will notice something
- If we compare these two forms, the partial differential coefficient must be equal to the natural variable that is NOT the convenient natural variable of the thermodynamic potential
The implication of such relationships is huge, it means that we do not have to actually measure the change in the energy term, X, against one natural variable while keeping the other constant
- If we know the value of the "inconvenient" natural variable or , then we know how must change with and respectively
- Alternatively, if we know how varies with and , we will know the value of and of our system
- If we know how any one of these energies varies in terms of its natural variables, we can use the various definitions and equations from the laws of thermodynamics to construct expressions for any other energy terms
¶ Internal Energy
- As proven above, the fundamental equation of internal energy is
- In partial differential form, the expression becomes
- We can therefore relate each partial differential coefficients with one of the "inconvenient" natural variable
¶ Enthalpy
- As proven above, the fundamental equation of internal energy is
- In partial differential form, the expression becomes
- We can therefore relate each partial differential coefficients with one of the "inconvenient" natural variable
¶ Helmholtz Energy
- As proven above, the fundamental equation of internal energy is
- In partial differential form, the expression becomes
- We can therefore relate each partial differential coefficients with one of the "inconvenient" natural variable
¶ Gibbs Energy
- As proven above, the fundamental equation of internal energy is
- In partial differential form, the expression becomes
- We can therefore relate each partial differential coefficients with one of the "inconvenient" natural variable
¶ Thermodynamic Potentials and The 2nd Law
The natural variables have a relationship with the 2nd Law of Thermodynamics
- The 2nd Law states that the entropy of any isolated system is always increasing
- We can express this idea in terms of any thermodynamic potential
When both of the convenient natural variables of a thermodynamic potential are set to be constant, we can express the criterion of spontaneity in terms of the inequality of the differential of the thermodynamic potential
- is the thermodynamic potential, while and are its corresponding natural variables
- The inequality shows that the criterion for spontaneity and equilibrium
¶ Internal Energy
- Starting with the Clausius inequality
- Under constant volume, the heat flow is equal to the change in internal energy
- If we impose the constraint of constant entropy within the system, the inequality becomes
- We can then multiply both sides by T to get the inequality
- When the system's volume and entropy is constant, events that lead to a decrease in internal energy are spontaneous while events that cuases the internal energy to remain unchanged are in equilibrium
¶ Enthalpy
- Starting with the Clausius inequality
- Under constant pressure, the heat flow is equal to the change in enthalpy
- If we impose the constraint of constant entropy within the system, the inequality becomes
- We can then multiply both sides by T to get the inequality
- When the system's pressure and entropy is constant, events that lead to a decrease in enthalpy are spontaneous while events that cuases the enthalpy to remain unchanged are in equilibrium
¶ Helmholtz Energy
- Starting with the Clausius inequality
- Under constant volume, the heat flow is equal to the change in internal energy
- We can then rearrange the inequality
- We then add to both sides
- The left side of the inequality is just the differential of the Helmholtz energy at constant volume
- If we impose the constraint of constant temperature within the system, the inequality becomes
- When the system's volume and temperature is constant, events that lead to a decrease in Helmholtz Energy are spontaneous while events that cuases the Helmholtz Energy to remain unchanged are in equilibrium
¶ Gibbs Energy
- Starting with the Clausius inequality
- Under constant pressure, the heat flow is equal to the change in enthalpy
- We can then rearrange the inequality
- We then add to both sides
- The left side of the inequality is just the differential of the Gibbs energy at constant pressure
- If we impose the constraint of constant temperature within the system, the inequality becomes
- When the system's pressure and temperature is constant, events that lead to a decrease in Gibbs Energy are spontaneous while events that cuases the Gibbs Energy to remain unchanged are in equilibrium
This set of relations reveals that no thermodynamic potential is better at indicating the direction of a process than the other
- The true definition of spontaneity and equilibrium is based on the Clausius inequality, we are simply taking advantage of the change in thermodynamic potentials under certain restrictions to indirectly show how the total entropy is changing
- Although it is tempting to think that the free energies have some intrinsic connection to spontaneity, this is untrue. The only reason why free energies are used to predict spontaneity and equilibrium more often than internal energy or enthalpy is simply because an isothermal system is easier to achieve than an system with constant entropy. The same reason explains why Gibbs energy is used more often than Helmholtz energy, constant pressure is easier to achieve than constant volume
¶ The Thermodynamic Wheel
If you have been paying attention, you will have realized that there are certain patterns between the natural variables and the thermodynamic potentials
- Pressure ( ) is always paired with volume ( ), while temperature ( ) is always paired with entropy ( )
- The natural variables always come in pairs, with pressure term multiplied by volume term and temperature term multiplied by entropy term
- In each pair, one and only one of the natural variable will be the convenient natural variable of the thermodynamic potential
- The rate of change of the thermodynamic potential with respect to a convenient natural variable is equal to the other natural variable in the pair
Free energies ( & ) must have temperature ( ) as one of their convenient natural variable, while total energy terms ( & ) must have entropy ( ) as one of their convenient natural variable
Thermodynamic potentials that are related to internal energy ( & ) must have volume ( ) as one of their natural variable, while thermodynamic potentials that are related to enthalpy ( & ) must have pressure ( ) as one of their natural variable
- This property is related to the fact that heat flow at constant volume is equal to the internal energy, while heat flow at constant pressure is equal to the enthalpy
We can construct a mnemonic device that summarizes these patterns
- The corners of the square are the natural variables, while the edges of the square are the thermodynamic potentials
- The two natural variables adjacent to a thermodynamic potential are the two convenient natural variables of said thermodynamic potential
- One can interpret this square in any way they please and will find endless patterns
Alternatively, we can use the thermodynamic wheel to interpret the meaning of the thermodynamic potentials
¶ Chemical Potentials
Many equations we have use thus far can be applied only to closed systems of constant composition
- We have restricted ourselves to systems containing only one chemical component
In general, to fix the state of a system, the values of two independent variables and the mole numbers of the components must be fixed
- We have been able to neglect the mole number of components because we have discussed only closed systems of fixed composition
- We shall now extend our discussion to many-component systems, in particular those systems in which the chemical composition changes
¶ Partial Differential with respect to Mole Number
We can describe any state functions as a function of other variables
- When we are dealing with systems with a single component, we can define a thermodynamic potential as a function of its natural variable
- For a multi-component system, that state function will now depend on not only pressure and temperature, but also the number of mole of each component
We can express the differential of any thermodynamic potential in terms of sums of partial differentials
- For a single-component system
- For a many-component system
The partial differential of an extensive state function with respect to the mole number of a component is the rate of change of that extensive state function with respect to the mole number of that component
- Although we can define such a partial differential for any extensive state function, we are particularly interested in the partial differential of thermodynamic potentials with respect to number of mole of a component
- The partial differential of any thermodynamic potentials with respect to number of mole of a component is the same, and it is called the chemical potential of the component
The chemical potential of the ith component is defined as
- Both the natural variables of the thermodynamic potential and the mole number of other components are held constant
We can therefore define chemical potential in terms of , , or
- Internal Energy
- Enthalpy
- Helmholtz Energy
- Gibbs Energy
¶ Significance of the Chemical Potential
Chemical potential is a form of potential energy that can be absorbed or released during a chemical reaction or phase transition due to a change in mole number
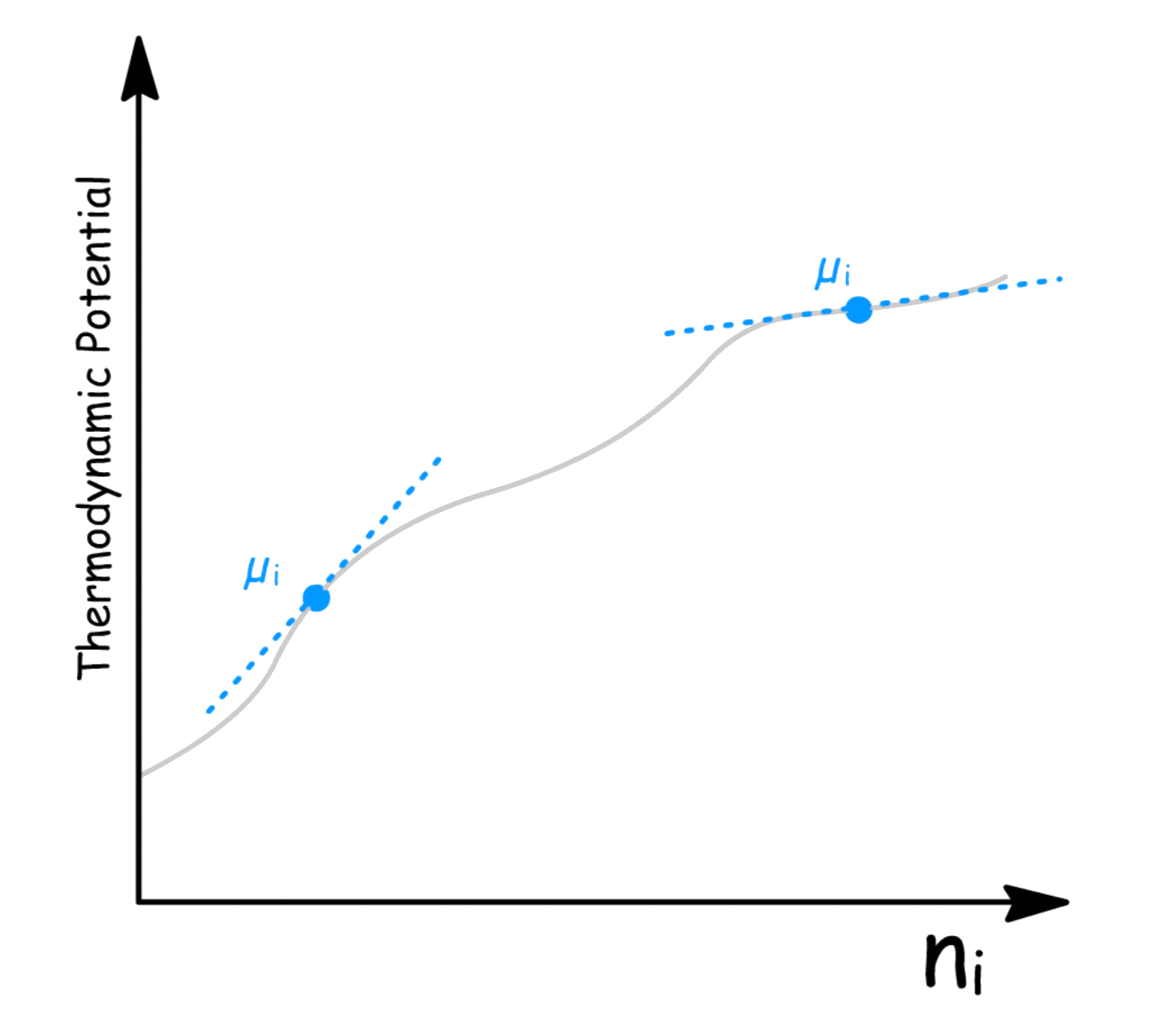
Since the chemical potential is related to rate of changes, when we plot a graph of a thermodynamic potential against the mole number of a component, the gradient will be equal to the chemical potential of the component
- We can see that the chemical potential varies with composition
- We can therefore interpret µi as the increase in thermodynamic potential that occurs when one mole of component i is added to an infinitely large quantity of mixture so that the composition does not change
The value of chemical potential of a component in a multi-component system does not change independently
- Consider an arbitrary fundamental thermodynamic equation of a multi-component system
- If we set the two natural variables of the thermodynamic potential constant, the change in energy will only depend on the change of the composition of the system
- The total differential of is
- We therefore obtain the equality
- The equation shows that the chemical potential of one component cannot change independently of the chemical potential of other components