One of the most powerful tools we have for studying natural phenomena is thermodynamics
- It requires no assumptions regarding the nature of the particles that make up a system, nor does it even need the premise that particles exist, hence its explanations of nature are generally applicable
- However, this also means that thermodynamics can only deal with measurable properties of matter in bulk
Despite its name, it is concerned with the equilibrium positions of systems, not their dynamics
- The primary objective of thermodynamics is to establish a criterion for determining the feasibility or spontaneity of a given physical or chemical transformation
- Once the spontaneous direction of a natural process is determined, we may wish to know how far the process will proceed before reaching equilibrium
Thermodynamics gives chemists a set of relations between macroscopic properties that we can measure in a laboratory
- These relations can all be derived from a few initial postulates, the Laws of Thermodynamics
¶ Thermodynamic Properties
In thermodynamics, we will encounter and use different properties
- These properties can all be categorized into two groups: state functions and path functions
¶ State Functions
A state function is an observable of a system that only depends on the current state of a system and is independent of its history
- State quantities are properties that systems intrinsically possess. For any given state, there must be a definite value for each state quantity
- Since the state of a system is dictated by the values of the state quantities, the system does not "remember" its previous state
Since state quantities do not depend on the path they took to arrive there, their values must be determined entirely by the state of the systems
- It is therefore possible to write an explicit expression for a state quantity in terms of its independent variables
- Each independent variable of a state quantities is also a state quantity
In essence, state functions are just regular functions that we encounter most of the time and so they share the same properties
- The total differential of a state function can be expressed as such
- The overall change of a state quantity is the sum of all infinitesimal changes along to path
- The line integral over a closed path is zero as the initial state is the same as the final state
¶ Path functions
A path function is a well defined quantity that describe the process of an energy transfer process between two states
- Since the purpose of path functions is to quantitatively describe the transition between states, it should not be surprising that they depend on the path taken
- Path function can be thought of as a description of a process, so they are not a property a system can possess
By definition, path functions describe the change in states
- We use đ rather than d to represent infinitesimal changes for process quantities to remind us that we need to specify the path taken
- The total energy transferred via a particular path function, is the sum of all individual contributions at each point of the path
- By convention, we do not write \Delta \text
¶ Variables of State
The variables of state is a set of appropriate measurable properties a system intrinsically have
- The physical state of a substance is defined by its variables of state in the sense that two samples of the same chemical make-up that have the same set of variable of state are in the same state
There is an infinite way to define variables of state but we will only discuss one set of variables that are particularly useful to specify the state
- We would like to know the number of substance a system contains
- We would like to know the amount of space a system occupies
- We would like to know the magnitude of force exerted on the system
- We would like to know the average value of kinetic energy of the particles in the system
In the study of thermodynamics, we can categorizes two types variables
- Variables that are independent of the quantity of matter in the system are called the intensive variables
- Variables that are depend on the quantity of matter in the system are called the extensive variables
¶ Amount of Substance ( n )
The amount of substance, , is a counting quantity for particles
- By definition, the amount of substance depends on the quantity of matter in the system and is therefore an extensive variable
- We can use any counting unit for this purpose, but in practice it is invariably the mole
¶ Volume
Volume, , is a measure of the amount of three-dimensional space occupied by an entity
- In thermodynamics, we use volume to measure the space occupied by the system
The volume is a system's capacity to keep the matter
- Hence, volume varies either when the capacity of the object changes or the amount of matter within the object changes
- It is therefore an extensive property
¶ Pressure
We define pressure, , as the magnitude of force that is perpendicular to a surface exerted per area
- In thermodynamics, we are concerned with the pressure the system is exerting to its border () and the external pressure exerted onto the border of the system ()
- The pressure we encounter in thermodynamics is uniform and is the same throughout the system
If two systems are separated by a common movable wall, the system with the higher pressure will compress the system that has the lower pressure until both side have the same pressure
- This is because the existence of pressure difference implies there is a net force
¶ Temperature
Temperature is formally a property that determines in which direction energy will flow as heat when two samples are placed in contact through thermally conducting walls
- Heat flows from the sample with the higher temperature to the sample with a lower temperature
From a microscopic point of view, temperature is related to the average kinetic energy of molecules in the system
- The higher the temperature, the higher the average kinetic energy the molecules possess
¶ Work and Heat
Although they may seem completely different, work and heat actually shares a lot of similarities
- Both work and heat are path functions that describe the transfer of energy
- They are two different forms of energy in transit, but not a form of energy that can be possessed. Upon entering or leaving a system, heat and work will be converted to kinetic and potential energy
From a molecular viewpoint, work and heat differ mainly in how orderly they affect the molecules that receive the energy
- Work may be regarded as the energy associated with orderly movement of bodies
- Heat flows are associated with the movement of thermal energy, which arises from the disorderly random motion of molecules
¶ Work
Work ( ) is done to achieve motion against an opposing force
- It is a process that transfer energy due to an opposing force
A process does work if in principle it can be harnessed to move a mass against a force somewhere outside
- If the system is the one doing work, the outside refers to the surrounding
- If the surrounding is the one doing work, the outside refers to the system
The work required to move an object an infinitesimally small distance of ds against an opposing force, , is given by the dot product between the opposing force and the change in distance
- Due to the nature of dot product, only the component of the opposing force that along the direction of displacement will contribute to the work done
When we add up all the infinitesimally small amount of work, we can express work as an integral of the opposing force over a distance
- When the force applied is uniform, we can treat the force term as a constant
In molecular terms, work is the transfer of energy that causes the particles on the outside to move in an organized manner
- When the system does work on the surrounding, it stimulates orderly motion in the surroundings
- When the surrounding does work on the system, it stimulates orderly motion in the system
Note that although in theory work should induce an orderly motion of particles on the receiving side, the collision between those particles can quickly randomize their directions
- In these situations, work is in effect stimulating the thermal motion of the receiving end
- We report that work is being done despite stimulating the thermal motions of particles
There are different types of work, but the one that we are most interested in is expansion work
- Expansion work is the work arises from the change of volume of the system, so it also includes work associated with the negative changes of volume, also known as, compression
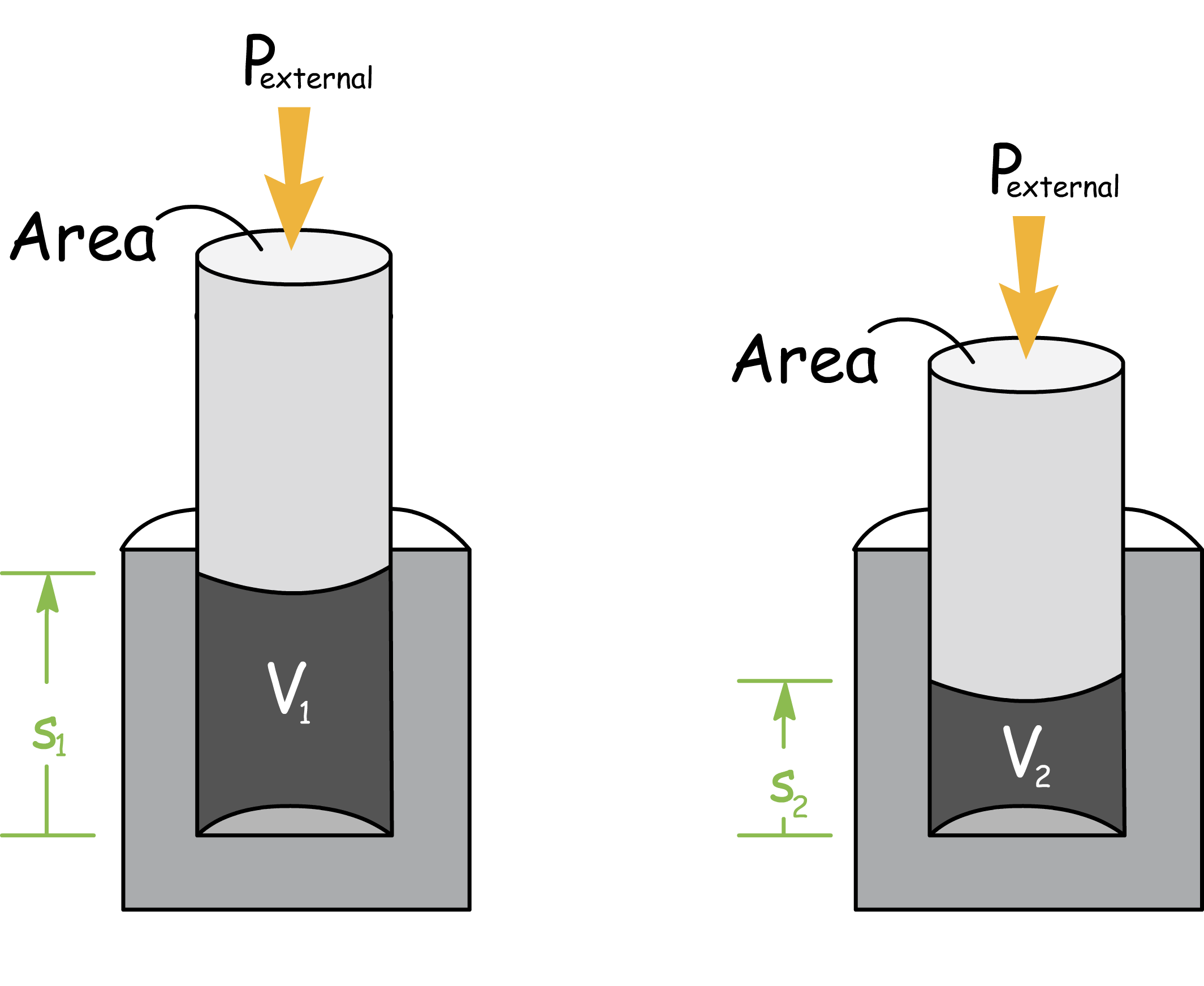
- Consider a system of gas in which one wall of the container is a massless, frictionless, rigid, perfectly fitting piston of area of A
- If we substitute the force in the expression of work with pressure and area, we will obtain
- Area multiplied by the distance that is perpendicular to it is just the volume, so we end up with the expression for expansion work. We shall also add a negative sign since compression work should be positive, this will become apparent in later chapters
- To obtain the total expansion work done when the volume changes from an initial value of Vi to Vf, we integrate the expression between the initial and final volumes
¶ Heat
Heat ( ) is a process that transfer energy due to a temperature difference
- The effect of this transfer of energy is a decrease in temperature of the hotter body and an increase in energy of the colder body
- There will be no net transfer in heat energy once the temperature of the two objects in question reaches the same temperature
Whether a process releases to or acquire heat from the surrounding can be termed as either exothermic or endothermic
- An exothermic process is a process that releases energy as heat into the surrounding
- An endothermic process is a process in which energy is acquired from its surroundings as heat
In molecular terms, heat is the transfer of energy that causes the particles on the outside to move in an apparently random and disorderly motion
- This disorderly motion is called thermal motion. The thermal motion of the molecules in the hotter side stimulates the molecules on the cooler side to move more and more vigorously, thus increasing the energy of the cooler side
Heat can conduct between two objects because of collisions between the molecules at the interface
- Momentum is exchanged at the interface
¶ The First Law of Thermodynamics
The First Law of Thermodynamics can be summarized as such :
- We can therefore call the first law of thermodynamics, the law of conservation of energy
¶ Internal Energy
In thermodynamics, the total energy of a system is called its internal energy,
- The internal energy of a system is the total kinetic energy and potential energy of the constituents of the system
- It does not include the kinetic energy arising from motion of the system as a whole
The internal energy of a system or surrounding is its capacity to do work or transfer heat
- When heat is transferred to or when work is done on an otherwise isolated system or surrounding, their capacity to do work or transfer heat increases
- When an otherwise isolated system or surrounding does work or releases heat, their capacity to do work or transfer heat decreases
Heat transfer and work done are the only two modes of energy transfer
- According to the first law, energy must be conserved, this means that all changes in the internal energy must be attributed to the combined effect of heat transfer and work done
- Mathematically, we can describe it as such
¶ Change in Energy
In thermodynamics, when we consider changes from one state to another, we are interested in two things
- How much energy is gained or lost by the system
- How much of this energy is transferred via heat and how much of it is transferred via work
All energy change is with respect to the system
- When energy is lost to the surroundings, the sign is negative
- When energy is gained from the surroundings, the sign is positive
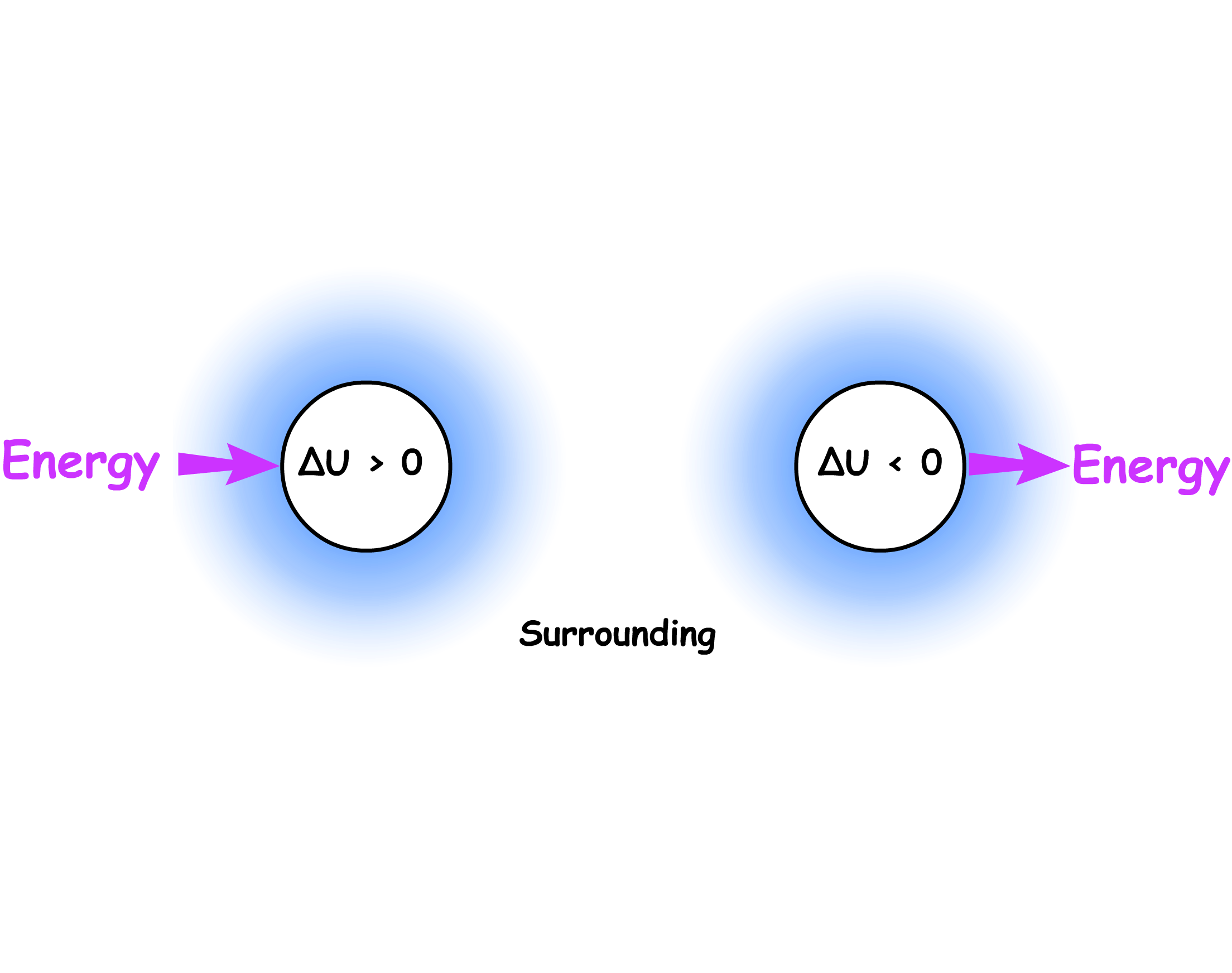
The sign of is determined by the net direction of energy transfer
- If the internal energy of the system increases, then the internal energy change is positive ( )
- If the internal energy of the system decreases, then the internal energy change is negative ( )
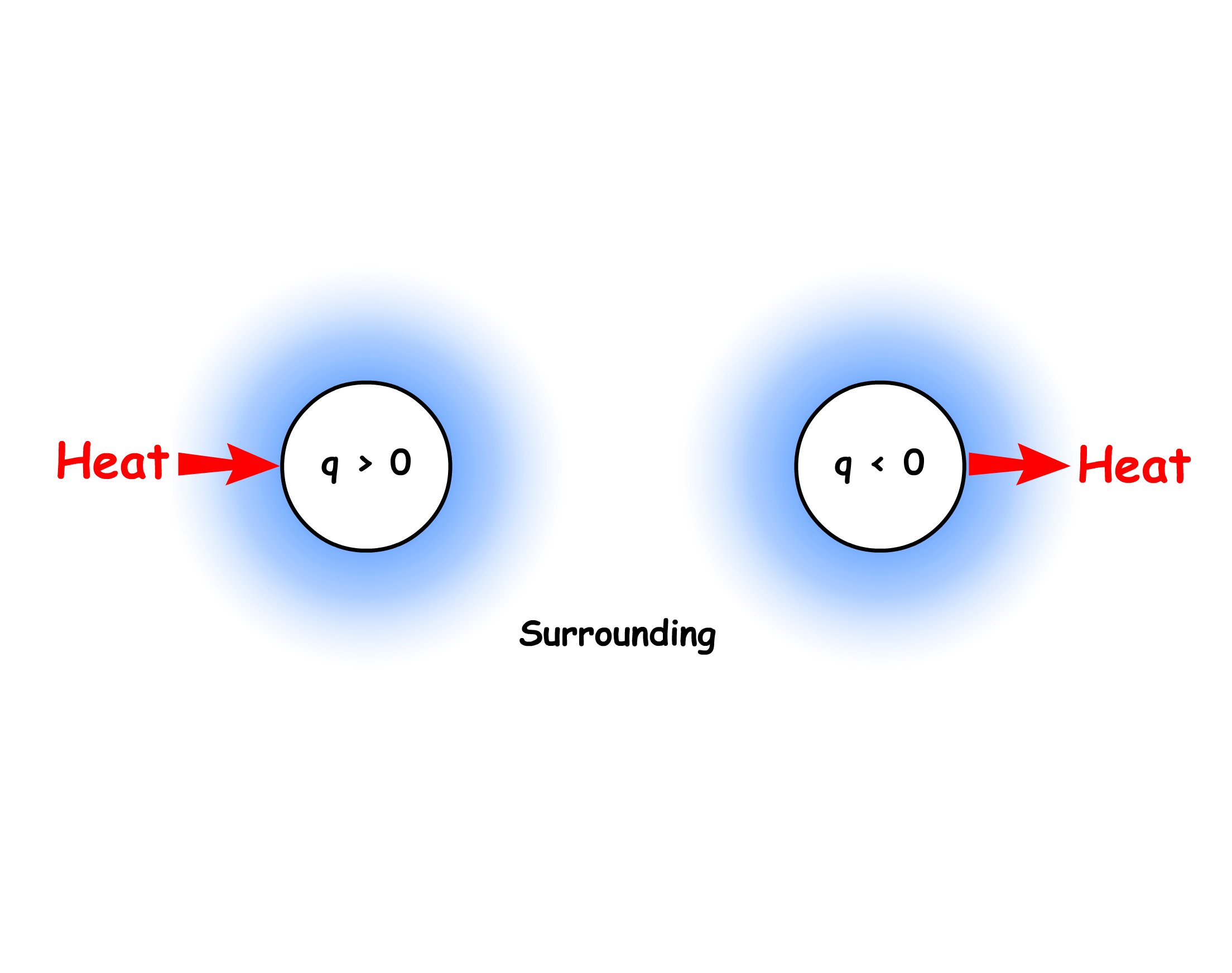
The sign of is determined by the direction of heat flow
- If heat is flowing into the system, the heat energy exchange is positive ( )
- If heat is flowing out of the system, the heat energy exchange is negative ( )
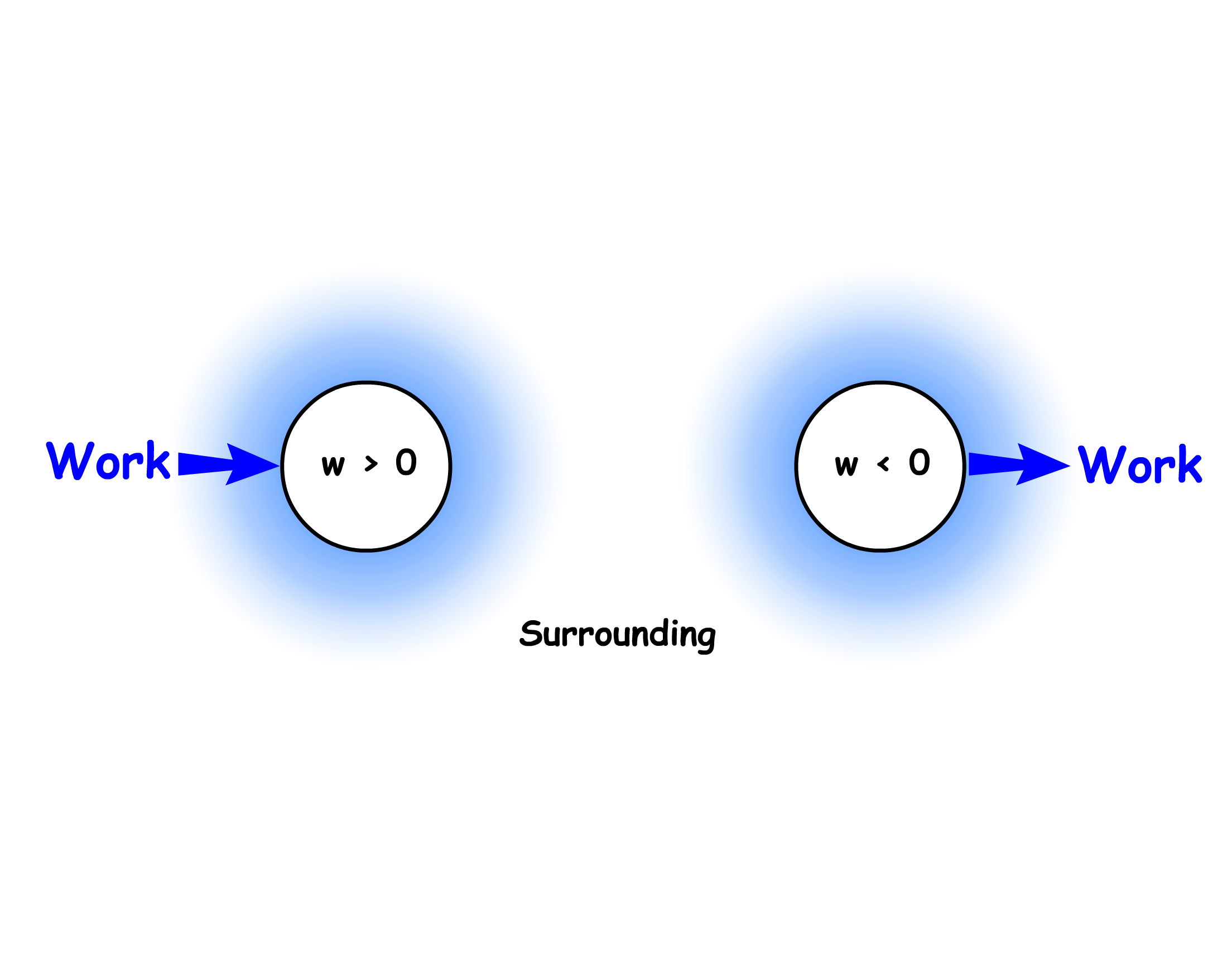
The sign of is determined by the party that does the work
- If work is done on the system, then the work energy exchange is positive ( )
- If work is done by the system, then the work energy exchange is negative ( )
¶ Reversible Process
A reversible process is one which is symmetric in time, where doing the reverse process is the same as running the clock backwards
- A system is only time-symmetric ( i.e. does not change with time ) when it is in equilibrium
- Thus, for a process to be reversible, it must take place without a departure from equilibrium
- Put another way, a reversible process must be a process that transitions continuously through a series of infinitesimally separated equilibrium states, each with well-defined state variables
- We call each of these separated equilibrium states as quasistatic state
In order to go from one quasistatic state to another, we must make infinitesimally small changes to the corresponding state variable
- Consider a reversible process where the overall process results in an overall change of a state variable,
- Equilibrium states are states where everything is in perfect balance ( i.e. no net force between system and surrounding, no temperature gradient between system and surrounding e.t.c. )
- Since we want to transition smoothly from one equilibrium state to another, we must only make infinitesimally small changes at each step such that the system and the surrounding are still in perfect balance upon making that infinitesimally small changes
- Although each quasistatic state only differ by an infinitesimally small change from its immediate "neighbour", these changes add up and results in a large change
At any given quasistatic state, the immediate "forward" and "backward" quasistatic state differ by the same amount, so the forward process is equally achievable as the backward process
- Reversing any step will restore the system and the surroundings to their previous state
It does not take additional energy to reverse a reversible process
- By definition, there are no changes in equilibrium, so there is no energy transfer between the system and the surrounding at each quasistatic state. Hence, all the energy transfer must be attributed to the infinitesimally small changes, , made during the transitions between quasistatic states
- Therefore the total change in energy between the initial and final state will simply be a result of the overall only and nothing else
- Since the forward and backward process share the same , the energy required to change the system reversibly from the initial to final state is the same as the energy released by the system when it changes reversibly back from final state to the initial state
- In other words, the energy required to go along one direction is fully covered by the energy released in the other direction, so no additional energy is needed to reverse a reversible process
When we say a process occurs irreversibly, it does not mean we cannot undo it, but it will require additional energy to restore the system to its original state
- Unlike reversible processes, each step in an irreverisble process is not in equilibrium, so energy transfer within each of these step is possible
- As a result, the total change in energy between the initial and final state will be a result of the overall and the energy transfer made in each step
- Hence, the energy required to change the system irreversibly from the initial to final state is not the same as the energy released by the system when it changes irreversibly back from final state to the initial state
- In other words, the energy required to go along one direction is not fully covered by the energy released in the other direction, so additional energy is needed to reverse a irreversible process
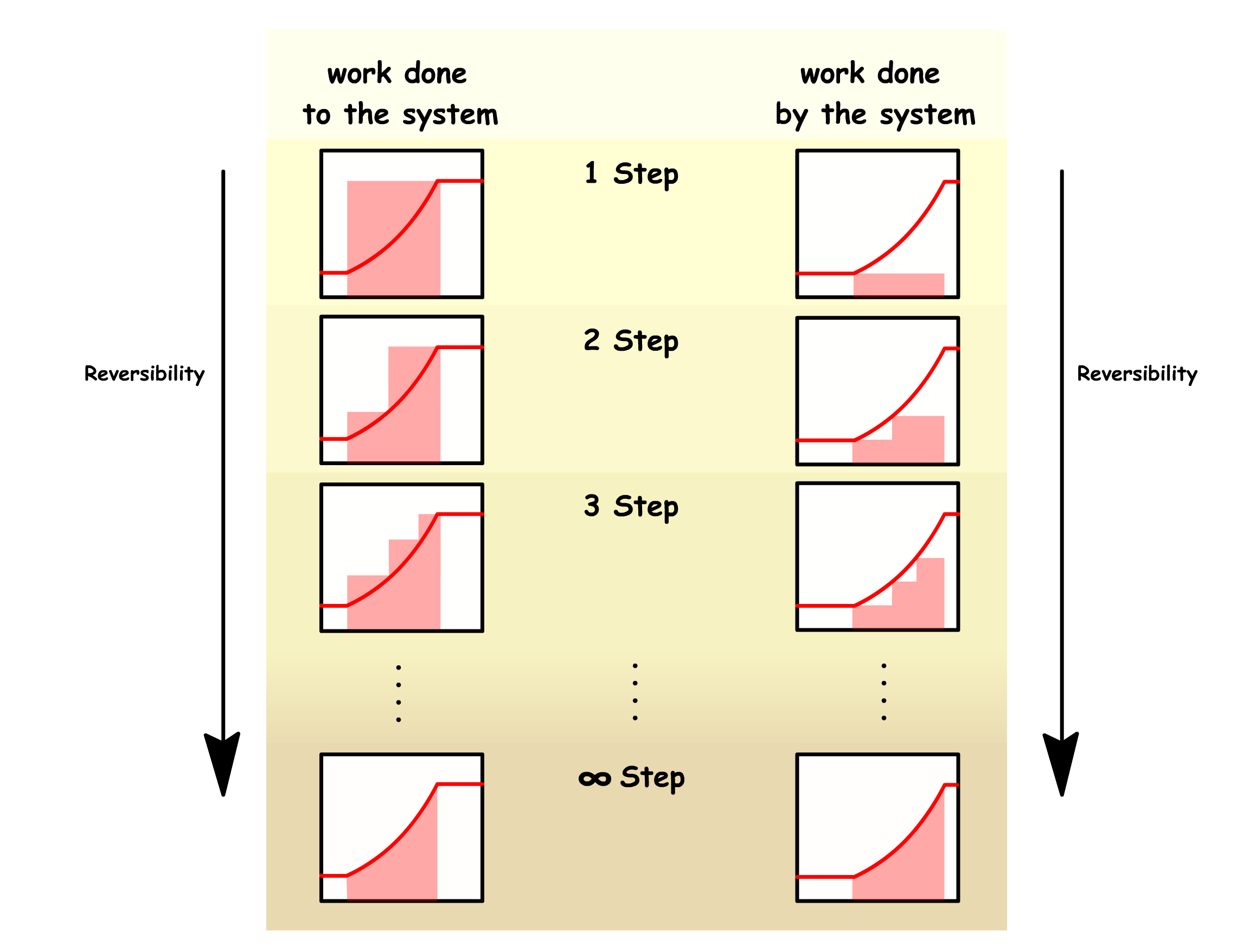
Reversible processes are impossible in real life
- They require an infinite number of steps to go from one state to another, which cannot be achieved in reality
- We can increase the reversibility of a process by increasing the number of steps we take in a process
There are an infinite pathways to change a system from one state to another
- We also know that internal energy is a state function, while heat and work are path functions. Hence, for any process that results in a certain change in internal energy, there are an infinite combinations of work done and heat flow
- Each combination of work done and heat flow can be viewed as a "path" that bridges from the initial state to final state
¶ Reversible and Irreversible Work
In a reversible process, the work done to a system in the foward direction and the work done by a system in the backward direction is equal in magnitude
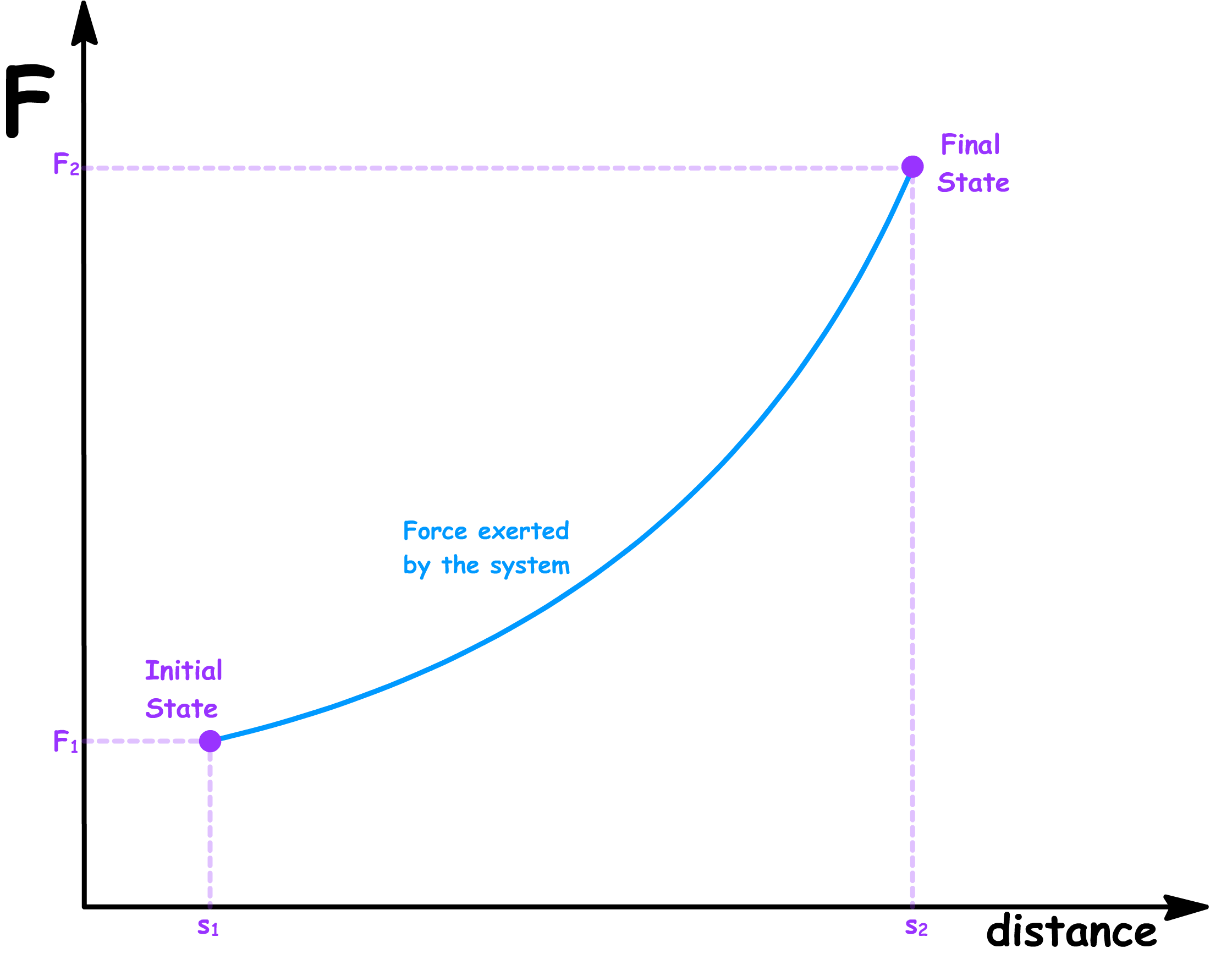
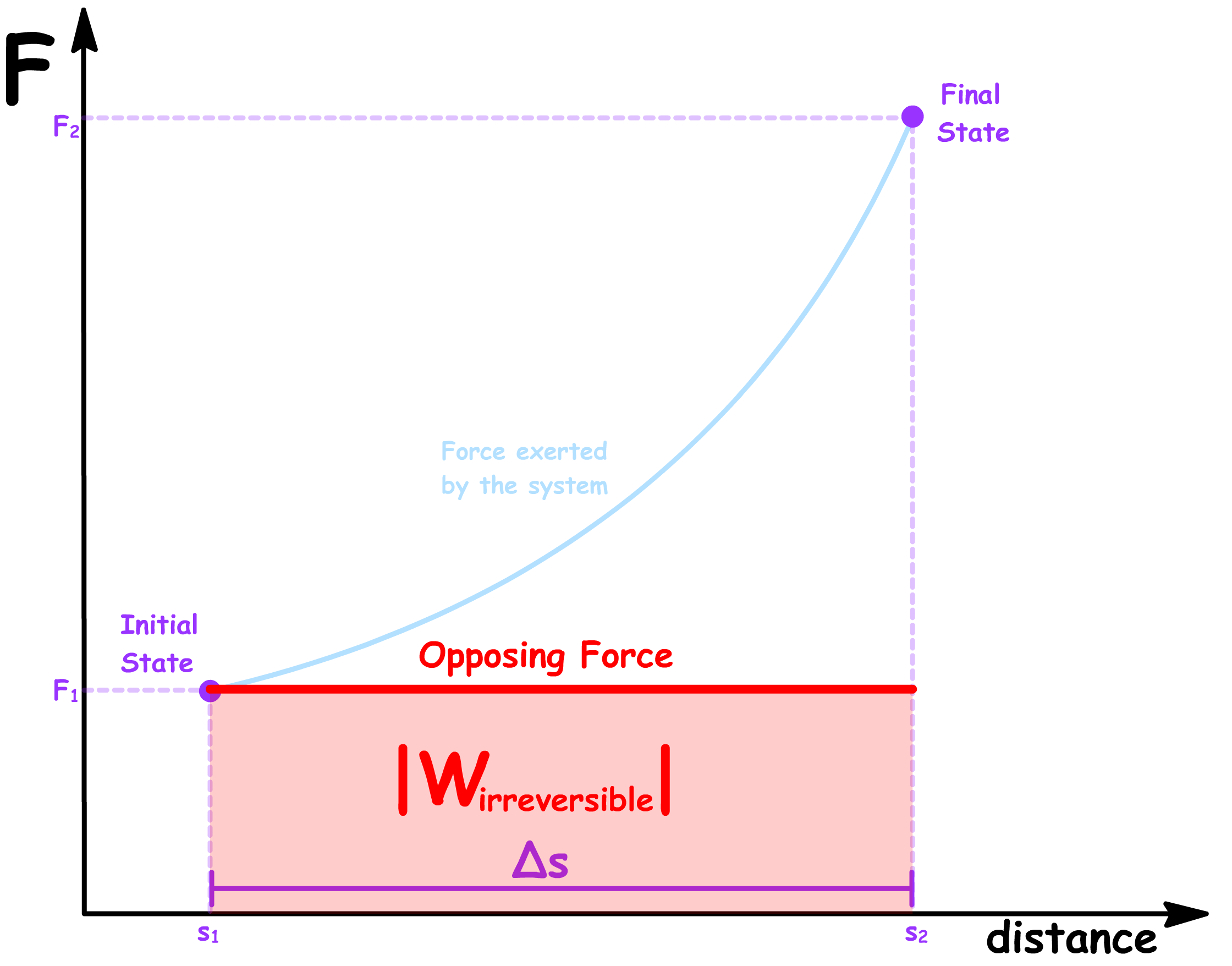
- Suppose the force exerted by the system is a function of the distance
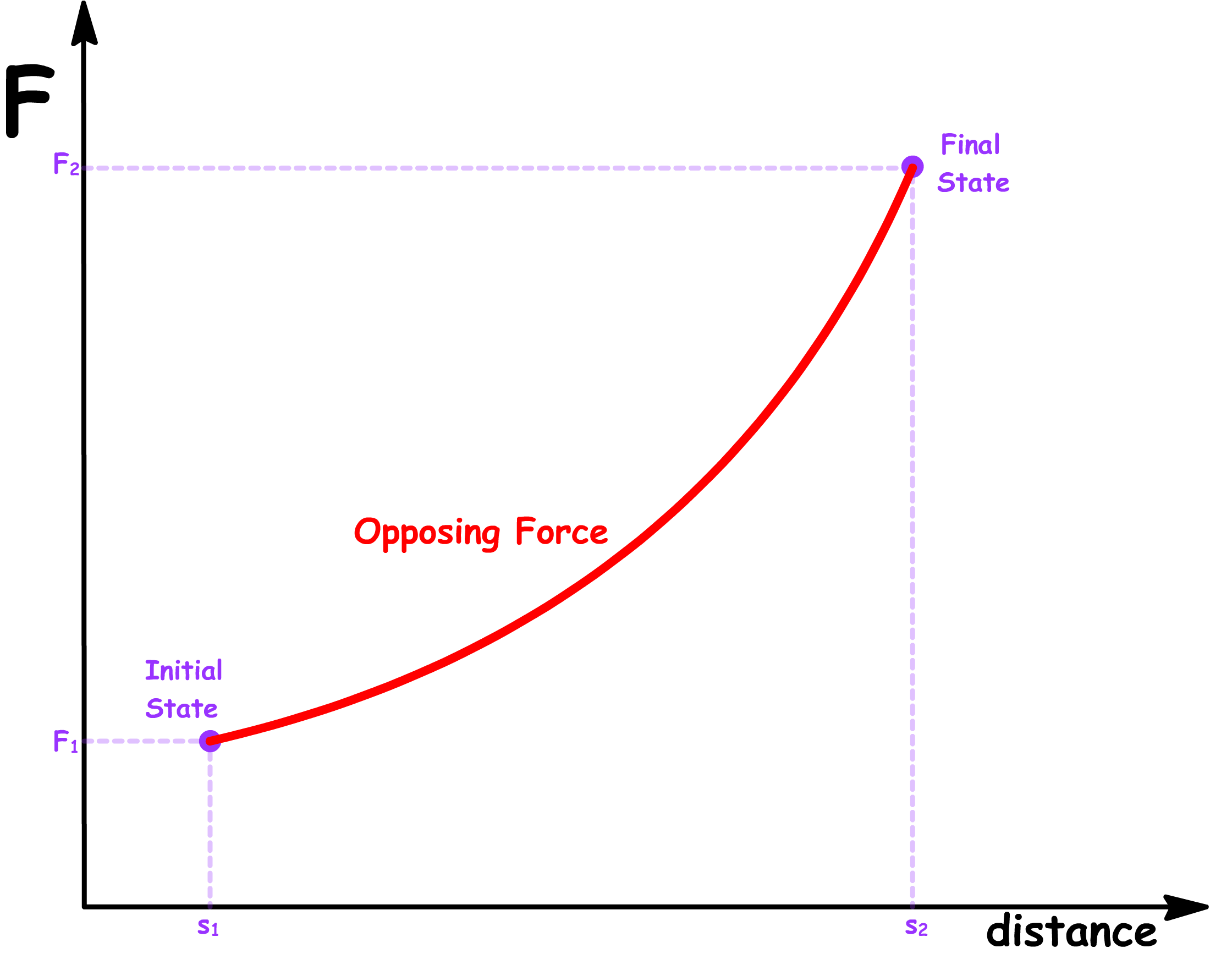
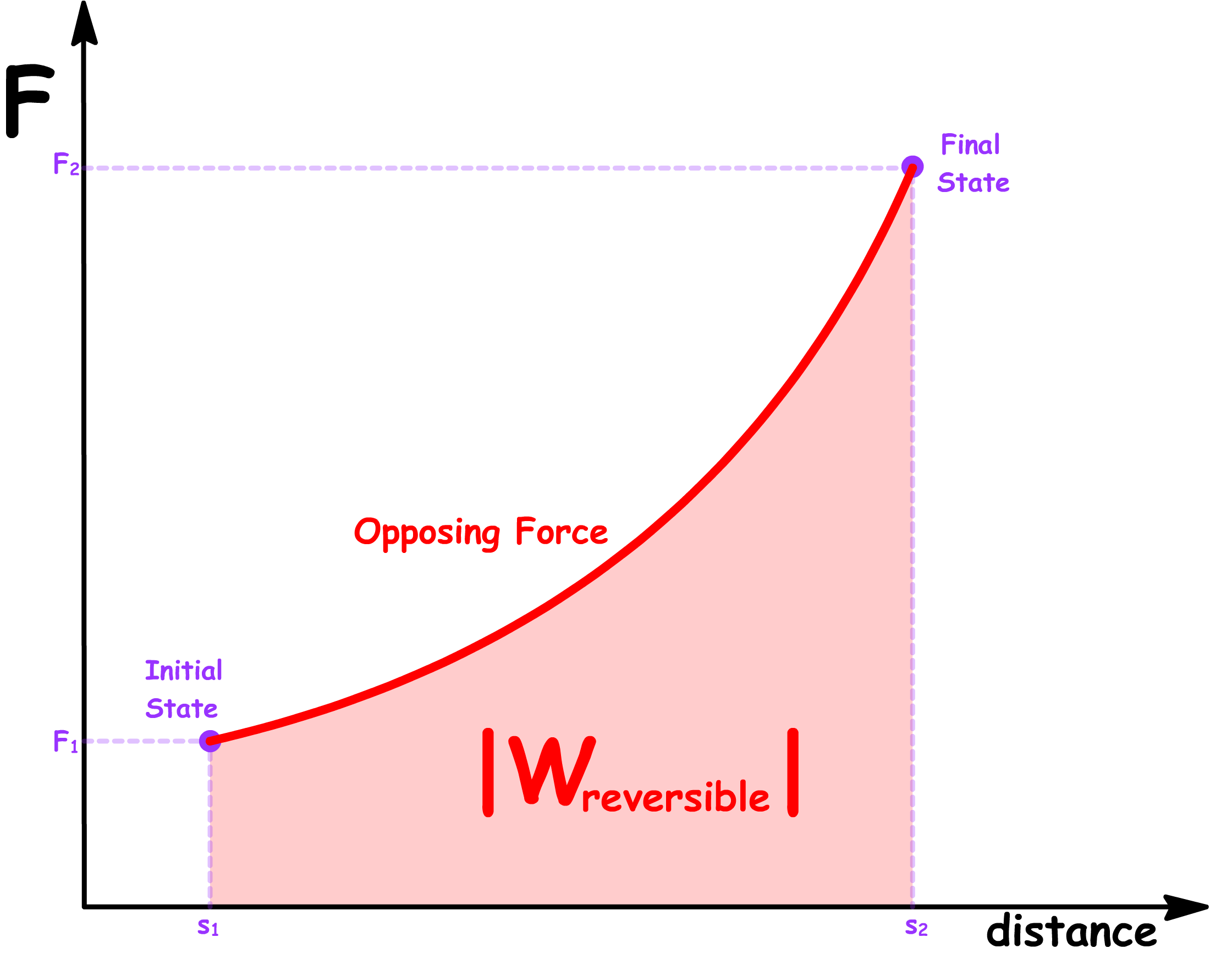
- In a reversible process, in order to maintain equilibrium at every step, there must be no net force at any given step. In other words, the opposing force must match the force exerted by the system at every distance
- The magnitude of the reversible work done by the system and the magnitude of the reversible work done on the system is therefore given by the area under the graph
In an irreversible process, the work done to a system in the foward direction and the work done by a system in the backward direction are not equal in magnitude
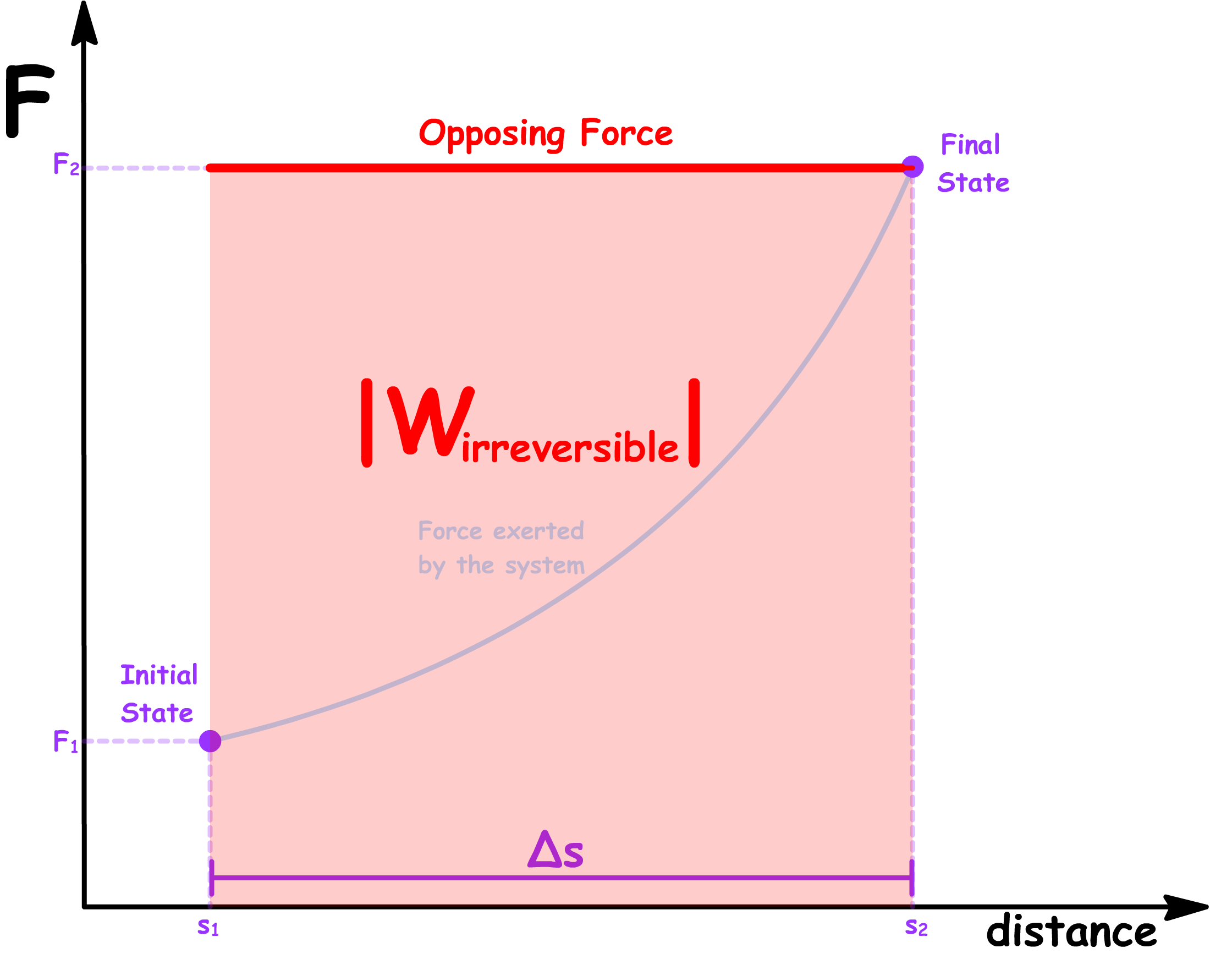
- In an irreversible process, large changes to the external conditions are made. In this case, instead of taking small steps of , we are making a large step of
- Since we are not changing the opposing force continuously along each step, the work done required to push the system from the initial state to the final state irreversibly will therefore be given by
- Since we are not changing the opposing force continuously along each step, the work done by the system when it returns from the final state back to the initial state irreversibly will therefore be given by
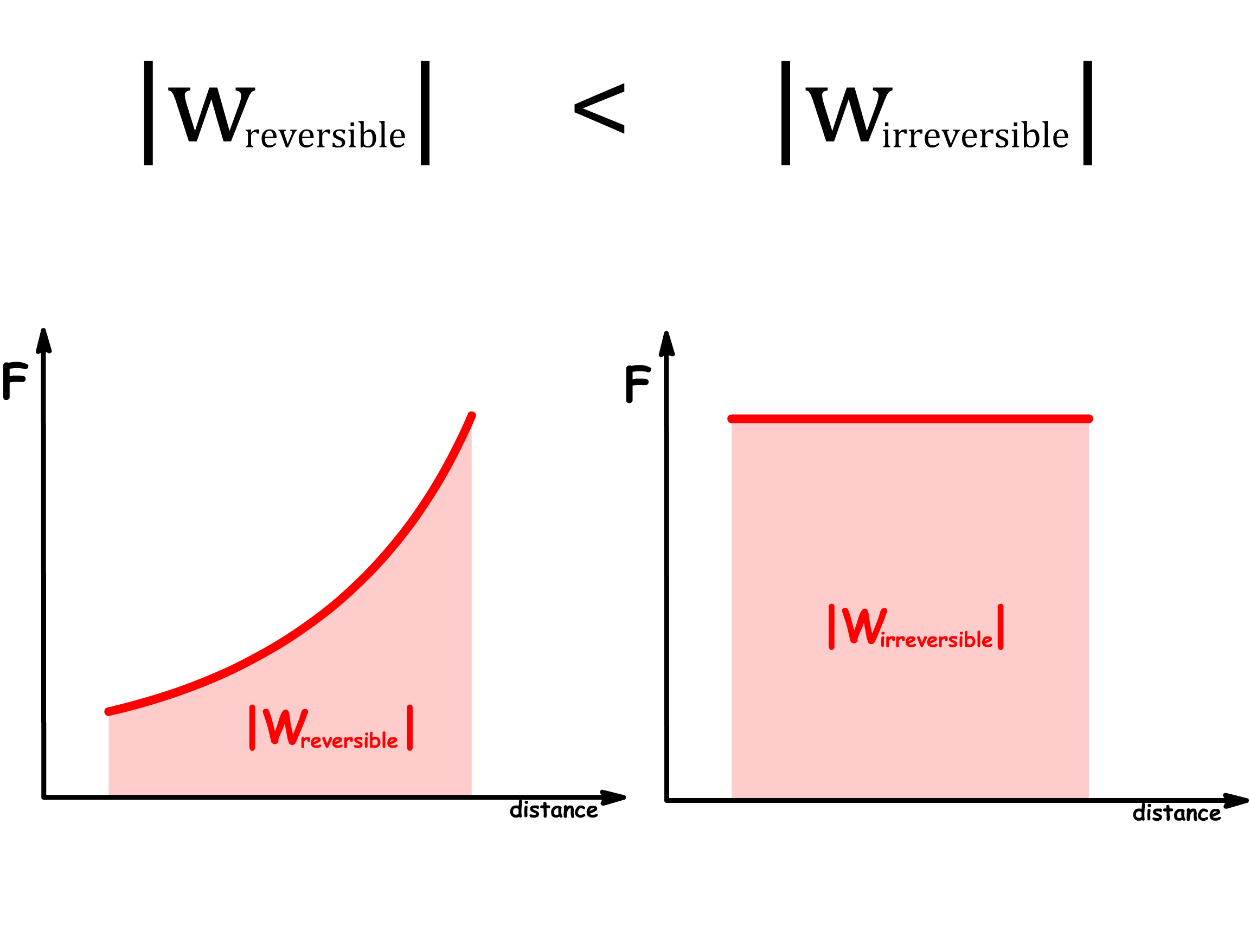
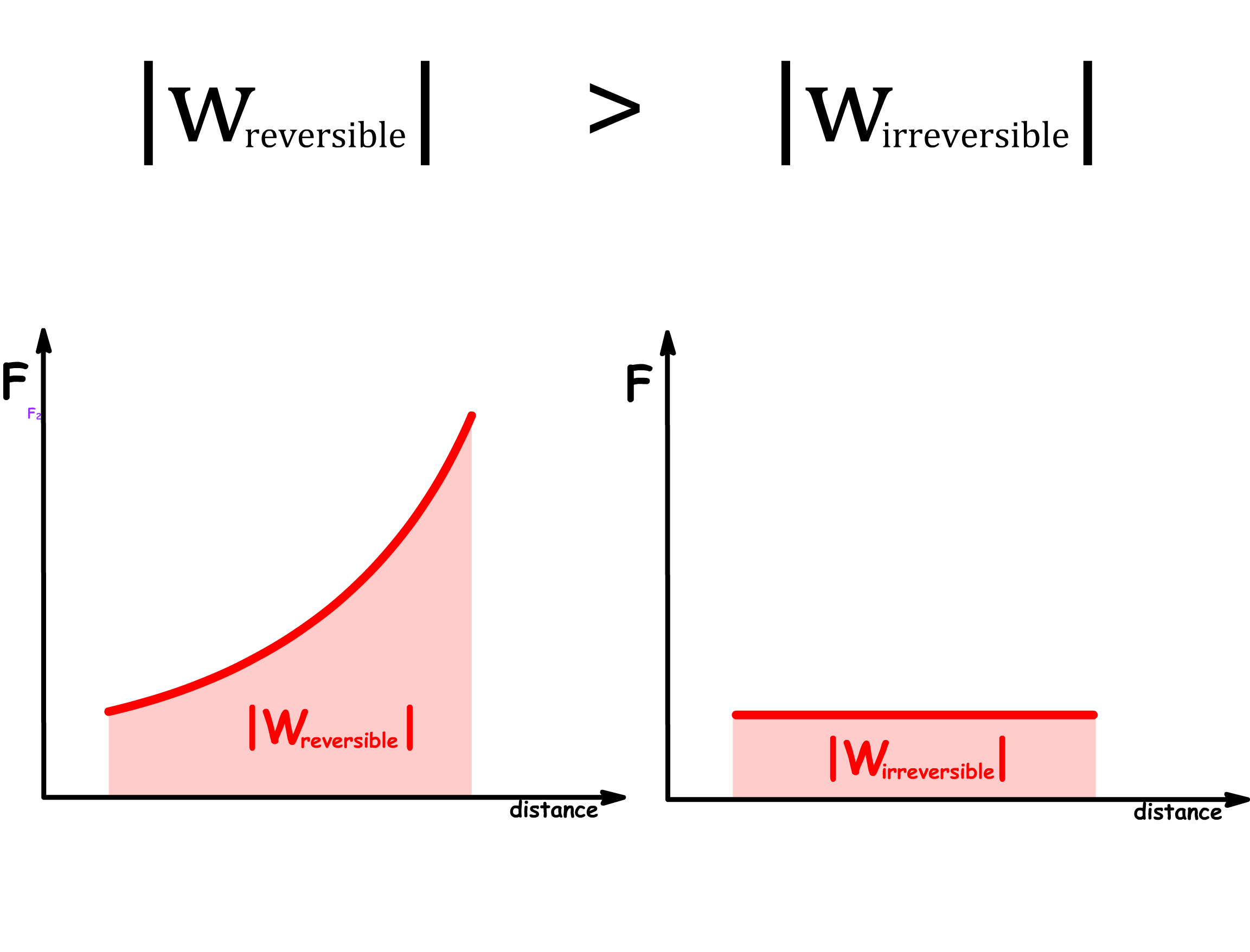
Reversible work is more effective than irreversible work
- An system requires more work if the process is irreversible
- An system produces less work if the process is irreversible
- In general, the relative size between the magnitude of reversible and irreversible work is given by
- Since work done on the system is positive, while work done by the system is negative, we can rewrite the inequality to
- In general, we can say
Simply by including more steps, we can make a process more reversible
- The irreversible work will approach the reversible work from both directions in the limit of infinite steps