The 1st Law of Thermodynamic states that energy is conserved in any process, but it does not tell us whether the process will occur in the first place or not
- This is an issue because we intuitively know that there are processes that obey the conservation law but will never happen
- We therefore need another fundamental law to tell us whether an event will occur
The conservation law doesn’t tell us why there is preference given to a particular direction of changes
- In other words, why things change in a particular manner as time moves forward?
- Put it another way, what distinguishes from time going forward and time going backward?
The total energy of an isolated system is constant, but the energy is parceled out in different ways
- The direction of spontaneous change is related to the distribution of energy
- In order to understand the tendency for the dispersion of energy, we must familiarize ourselves with the concept of entropy
¶ The Second Law of Thermodynamics
The Second Law of Thermodynamics can be summarized as such :
- This event will continue to occur until its occurence no longer stabilizes the universe. At this point, a state of high stability is attained and equilibrium is established
We can interpret the second law as a tendency to reach equilibrium
- Once equilibrium is disturbed, the return to equilibrium is inevitable
- The pathway to equilibrium always involves the occurance of an event that increases the stability of the universe
All processes can therefore fall under one of two categories
- A natural process is one that will increase the stability of the universe when it takes place
- An unnatural process is one that will decrease the stability of the universe when it takes place
¶ Origin of Entropy
We have established that whether an event can happen is determined by its ability to bring about stability to the universe, but that is hardly quantitative
- If there are multiple potential natural processes, only one will take place
- We therefore need to devise a way to let us determine which one of those is more favorable
In order to quantiy stability, we must define a new state variable, entropy ( )
- The more stable a state is, the higher its entropy
Entropy must be a state quantity because the stability of a state does not depend on how it came to be
- In other words, entropy is an inherent property just like temperature, pressure, volume e.t.c.
We can relate predict whether a process can happen by determining the change in stability in the initial and final state
- A process is natural if it will cause the universe to go from a state of low stability to a state of high stability
- A process is in equilibrium if the initial and final state of the universe has the same stability
- A process will not take place if it will cause the universe to go from a state of high stability to a state of low stability
- We can describe these statements mathematically since the difference in stability between two states is given by
We can therefore describe the second law mathematically
- A process can only take place if the change in entropy satisfies the inequality
- Unless the it is in equilibrium, the entropy of the universe always increases
Although we are able to quantify stability, it is hardly convenient to predict whether a process is favorable by determining the change in entropy of the entire universe every time
- In thermodynamics, we are primarily interested in the system, so it makes sense to break down the entropy of the entire universe into a sum of entropy
The consequence of splitting the total change in entropy is that a natural process can take place with a local decrease in entropy
- In other words, as long as the total change in entropy is positive, an event can occur even when either the system or the surrounding experience a decrease in entropy
¶ Reversibility and Entropy
The change in entropy of the universe for a reversible process is 0
- A process is reversible if it can proceed without departure from equilibrium
- As established before, the change in entropy of the universe is zero when it is in a state of equilibrium. Hence, the change in entropy of the universe must also be zero for the entire reversible process
The change in entropy of an irreversible process is positive
- An irreversible process does not proceed through a series of equilibrium states
- Once equilibrium is disturbed, the return to equilibrium is inevitable, and it always involves an increase in entropy
The fact that a reversible process and an irreversible process results in a differentchange in entropy change of the universe may seem paradoxical since we have established that entropy is a state quantity
- The key to this is understanding that both the reversible and the irreversible pathway brings the system to the same final state, but they do not bring the universe to the same final state
- A reversible process is one that occurs without changing the surrounding permanantly, while an irreversible process changes the surrounding permanantly
- As a result, the final state of the surrounding, hence, the final state of the universe, is different for a reversible and an irreversible process
¶ The Thermodynamic Definition of Entropy
The thermodynamic definition of entropy concentrates on the change in entropy, dS, that occurs as a result of a physical or chemical change ( or process in general )
- The definition of entropy instructs us to find the energy supplied as heat for a reversible path between the stated initial and final states regardless of the actual manner in which the process takes place
Entropy can be thought of as the degree of dispersal of thermal energy within the system. The definition is motivated by the idea that a change in the extent to which energy is dispersed depends on how much energy is transferred as heat
- Heat stimulates random motion of particles, thus increases the entropy
- Work stimulates organized and uniform motion of particles, so the entropy is unchanged
Entropy is the flow of heat that results in the system losing capacity to do work
- We can interpret entropy as the amount of energy that is wasted ( not able to do work, but dissipated as heat )
It is essentially a threshold for how significantly you can increase the dispersion of particle energy in a system by supplying heat into the system
- The higher the resultant entropy, the more influential the heat flow was, and the less heat you needed to impart into the system to get its energy distribution to a certain amount of dispersiveness
¶ Clausius Inequality
Reversible heat flow is greater than irreversible heat flow
- We have proven the inequality before
- We can rearrange it to
- From the 1st Law, we know that , and we also know that the change in internal energy does not depend on the reversibility of the process
- If we put all the variables to the same sides, we will get
- We know that the left side of the equation is greater than or equal to 0, so we can create a new inequality
- Put in another way
Since reversible heat is related to entropy, we can create an inequality for entropy as well
- If we divide the inequality concerning the heat flow by the temperature at which it is transferred, we will get
We can recognize that the left side of the inequality is equivalent to the change in entropy, so we can substitute it for that
The equality is applicable to reversible process, and the inequality is applicable to irreversible process
- For irreversible, spontaneous processes
- In order to satisfy the inequality, q must be irreversible heat flow
- For reversible processes, or at equilibrium
- In order to satisfy the equality, q must be reversible heat flow
- For nonspontaneous processes
- In order to satisfy the inequality, q must be negative, meaning that heat is flowing out of the system, which is only possible if work is done on the system
If we now consider an isolated system instead, no heat flow is allowed ( đq = 0 ), therefore đq divided by T is also equal to zero. We can therefore revise the above statements
- If dS > 0, then the process is irreversible and spontaneous
- If dS = 0, the entropy is constant, then the process is reversible and is at equilibrium
- If dS < 0, the process is not allowed
Thus, we can conclude that, for an isolated system, any spontaneous change will tend to produce states of higher entropy until the entropy reaches a maximum. At this point, the system will be in equilibrium and the entropy will remain constant at its maximum value
- The universe, being an isolated system, will have its entropy keep increasing until it eventually reaches a maximum. Hence, we can use the total entropy of the entire universe as an indicator of spontaneity
¶ Entropy in terms of other Variables
While defining entropy in terms of the reversible heat flow is intuitive, it stops short when the spontaneous processes we are dealing with does not involve any heat exchange or does not involve any change in energy at all
- In situations like this, we need to define entropy in terms of other variables
¶ Volume-Dependence of Entropy
The volume dependence of entropy is particular important when dealing with gas
- The diffusion and free expansion of gas often involves no heat exchange or change in energy
- However, the processes can be characterized by the change in volume
The relation can be derived as such
- For ideal gas, the internal energy is independent of the volume when the system is isothermal, therefore , so the work done must be balanced by the heat exchanged
- Assuming only expansion work can be done, our expression will then become
- Since the expansion is reversible, the pressure term can be internal, which allow us to substitute it using the perfect gas law
- We can then divide both sides of the equation by the temperature at which the process is taking place
- We can immediately see that the left side of the equation is the same as the change in entropy
- We can then integrate the expression
- Therefore, we can get the relation
From this relation, we can see that the entropy of a process increases when the volume increases
- Therefore, expansions and diffusion are spontaneous processes
- Entropy is a measure of the degree of distribution of thermal energy within a system, and this distribution can be accomplished by having the particles that carry these thermal energy to spread throughout the system and cover a larger space
¶ Pressure-Dependence of Entropy
We have already derived the relation between the change in entropy and the volume of the system
- Using the perfect gas law, we can replace the volume terms
- If we cancel out the terms, we will be left with
- We can make the expression looks a bit more similar to that of the relation between entropy and volume by changing the sign
The relation show us that the entropy increases if the pressure gets smaller
- Therefore, the process of dilution is spontaneous
- Pressure, by definition, is smaller when the molecules are far apart. Therefore, entropy will increase when the pressure ( and concentration ) becomes smaller
¶ Temperature dependence of Entropy
Although temperature is included in the definition of the change in entropy, it fails to tell us how temperature affects the entropy
- The relation between entropy and temperature is useful when the process is not isothermal
The relation can be derived as such
- We know that the heat capacity ( in general, not at constant pressure or volume ) can be expressed as such
- If we divide both sides by the temperature, we will get
- The left side of the equation is the same as the change in entropy
- If we integrate both sides, assuming that the heat capacity does not change with temperature (in reality, it does change a little bit)
- Hence, we will get this general relation
The relation show us that the entropy increases if the temperature increases
- This can be explained by the statistical interpretation of entropy
¶ The Statistical Definition of Entropy
The statistical definition of entropy is the interpretation of entropy from a microscopic viewpoint
In many ways, the statistical interpretation is more logical and somewhat more intuitive than its thermodynamic counterpart
- However, the two ways of interpreting entropy are equivalent and each enriches the other
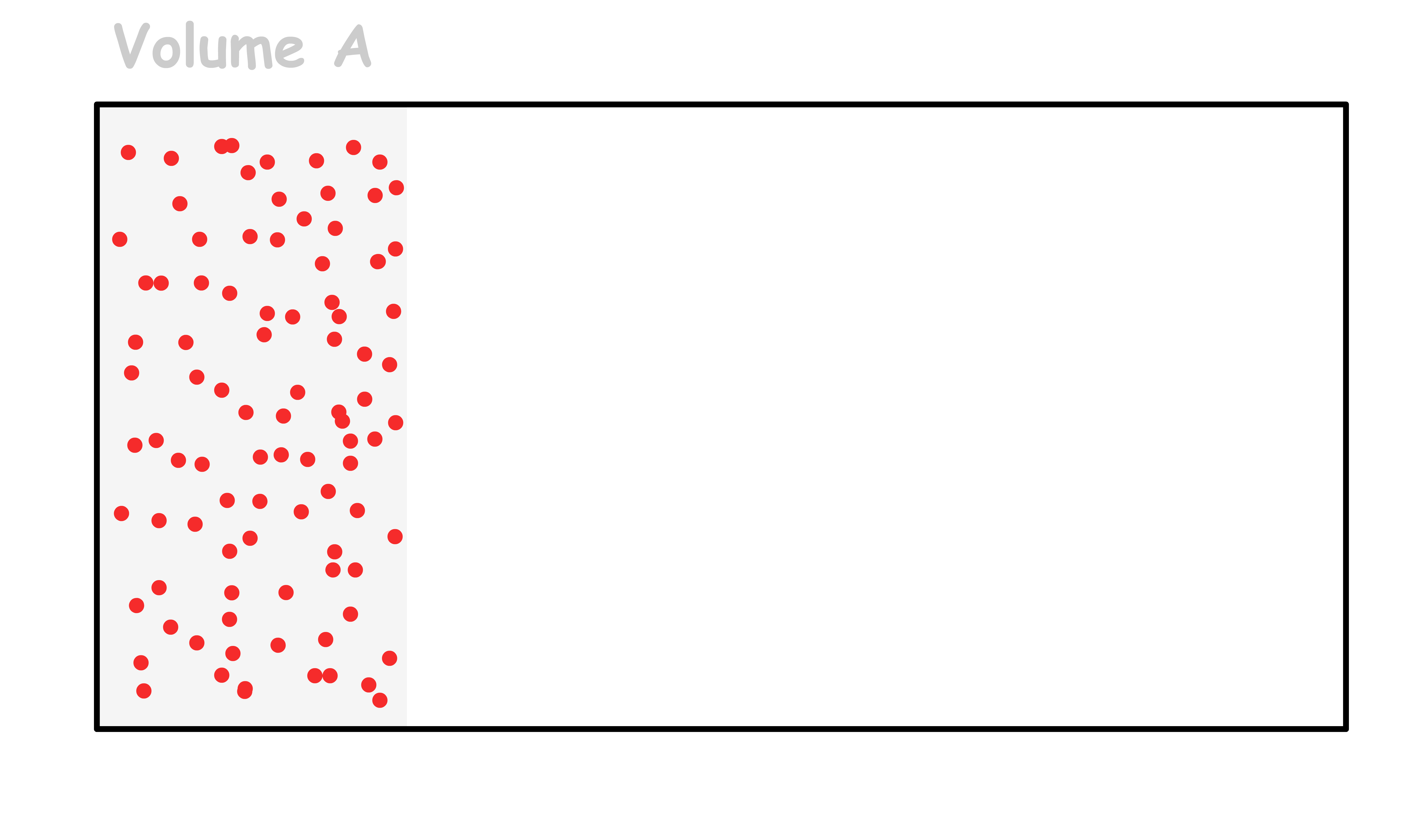
Consider a rectangular box with a total of n moles of particles within it
- The probability of finding all n moles of particles fitting within volume A is given by
- The probability of finding all n moles of particles fitting within volume B is given by
We compare the probability of finding all particles within a certain volume by dividing one equation by the other
- The numerical value involved is too large for computations, so it will be more convenient if we take the logarithmic value of both sides
- Using some logarithmic properties, we can simplify the expression
- We can then multiply both sides by R and divide them by NA, for reasons that will be apparent very soon
- The right side of the equation is just the change in entropy of a state going from volume A to volume B
- Since both and are universal constants, we can define a new universal constant out of them, the Boltzmann constant ( ). Moreover, probability plays a huge role in statistical entropy, so we give them a new symbol,
We can easily deduce the statistical definition of entropy
- Simply by looking at the equation, we can tell what the expression for each entropy is
- Hence, the general expression of entropy in statistical mechanics is
- is called the multiplicity
The statistical interpretation of entropy arises from the fact that energy is quantized, so matters can only occupy certain energy levels
- Although thermodynamics does not require the quantum mechanics, or even the existence of molecules to work, they offer new and intuitive perspective to understand thermodynamics
- The continuous thermal agitation of particles at T > 0K ensures that they are distributed across the available energy levels within the system
One of the most important consequences of this equation is that it allows us to calculate the absolute value of entropy
- Entropy thus stands alone among state functions as the only one whose absolute values can be determined
¶ Macrostates, Microstates and Multiplicity
In statistical mechanics, we view a system as the collection of some elementary constituents ( particles )
- Each elementary constituent has a set of possible states it can be in
The collection of states of all the constituents is the microstate
- Each microstate is one possible combination of states of all elementary constituents
- Each arrangement of the energy of each molecule in the whole system at one instant is called a microstate
The thermodynamic state of the system, which characterizes the values of macroscopic observables corresponds to many possible states of the constituents
- We refer to the macroscopic, thermodynamic state as the macrostate
Multiplicity (also called statistical weight) refers to the number of microstates corresponding to the same macrostate of a thermodynamic system
- The number of distinct microstates giving the same macrostate is called the multiplicity of the macrostate
A microstate is a specific microscopic configuration of a thermodynamic system that the system may occupy with a certain probability in the course of its thermal fluctuations
- Every microstate is equally likely to be adopted by the system
- However, some microstates are indistinguishable from each other and this causes macrostates that have more microstates, or a higher multiplicity, to be statistically more likely to be adopted by the system
Entropy is higher when the system is in a macrostate that has a large multiplicity
- The arrangement is most probable if it has the highest number of microstates
¶ Calculating the multiplicity
Combinatorics is the basis of entropy, and the concepts of order and disorder, which are defined by the numbers of ways in which a system can be configured
- The reason why the 2nd Law gives people the illusion that the universe tends towards disorder is because of the multiplicity of "ordered states" is much lower than that of "disordered states"
Combinatorics is concerned with the composition of events rather than the sequence of events
- In general, for a sequence of N distinguishable objects, the number of different permutations can be expressed in factorial notation:
- For N objects with categories, of which there are indistinguishable objects in the ith category, the number of permutations is
- In each category, the objects are indsitinuishable from each other, but but distinguishable from objects in the other categories
The probability of finding a system in a given state depends upon the multiplicity of that state
- That is to say, it is proportional to the number of ways you can produce that state
- Here a "state" is defined by some measurable property which would allow you to distinguish it from other states
- Multiplicity can be regarded as the number of permutation of a particular state
Ω is greatest when there are more ni terms and each of them encompass the least amount of particles possible
- Hence, entropy is maximized when particles are distributed across the largest amount of energy levels possible
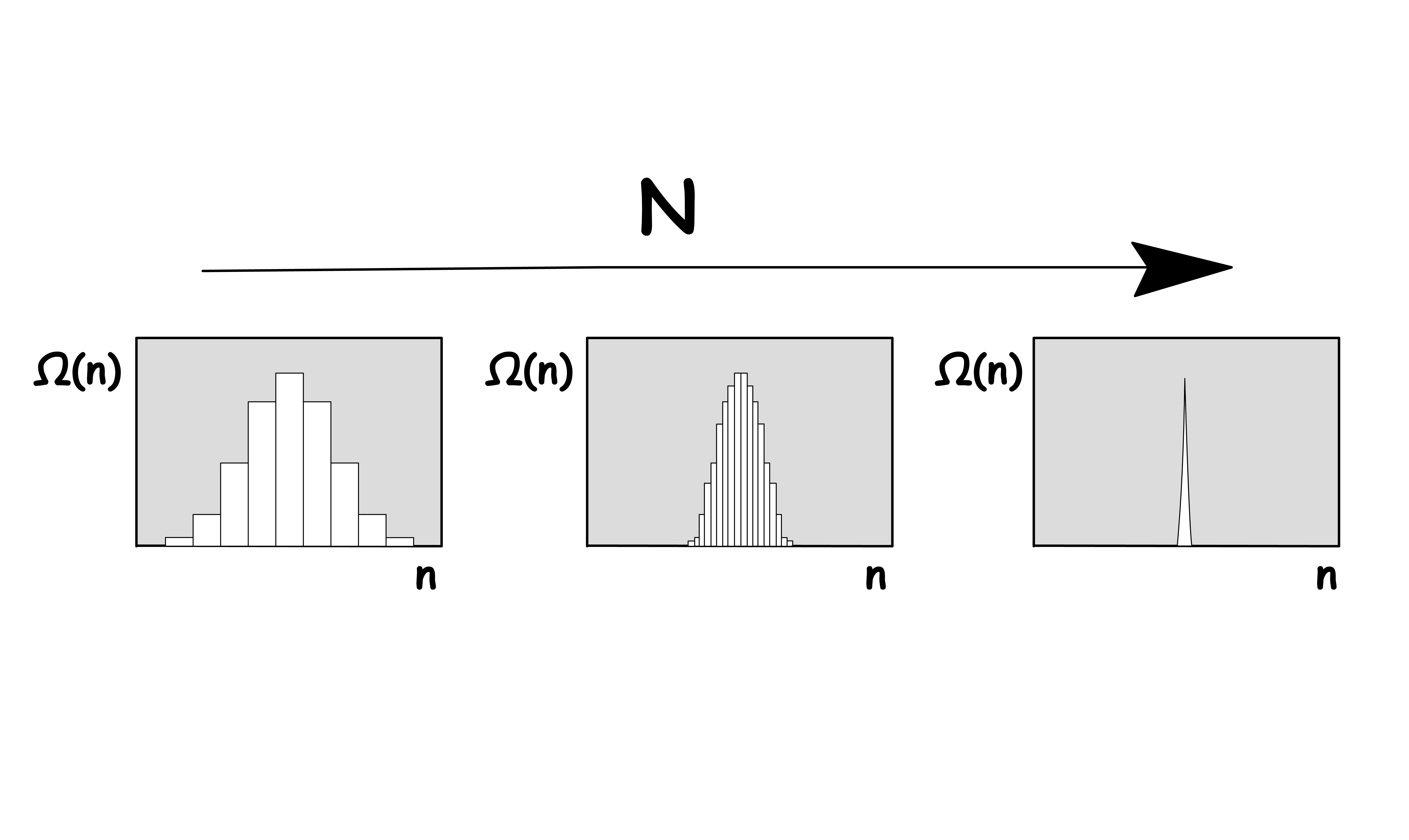
For the same number of indistinguishable objects, the multiplicity, , becomes increasingly peaked as you increase the total number of objects,
- As we increase the number of possible arrangement of particles ( N ), the amplitude of the peak becomes larger and larger
- Probable events become more probable, while unprobeable events become more unlikely as the number of possible arrangement ( N ) increases
- Macroscopic system contains a insanely large number of molecules, so the effect is even more extreme
We know that entropy will keep increasing until it reaches a maximum value, so the system will keep evolving until it reaches the microstate will the highest value
- Maximizing the multiplicity of the system is therefore a condition for equilibrium
¶ Energy Levels and Entropy
The origin of microstate comes from the quantized nature of energy levels
- There are only a finite of ways to distribute the particles in different energy level for a given total energy
To understand microstate properly, we must redefine the state functions and path functions from the point of view of microstate
The internal energy of the macrostate is the mean over all microstates of the system's energy
For a closed system, heat is the energy transfer associated with a disordered, microscopic action on the system, associated with jumps in quantum energy levels of the system
- The values of the energy levels remain unchanged, but the number of possible arrangement of occupants in the energy level increases
- Heat increases the number of microstate, so it will also increase the entropy
Work is the energy transfer associated with an ordered, macroscopic action on the system and will not cause jumps between energy levels of the system
- In this case, the internal energy of the system only changes due to a change of the system's energy levels, as if the whole set of energy levels all shifted upward
- Work does not affect the number of microstate, so it does not affect the entropy
In general, when we are measuring the properties of a system, we are measuring an average taken over the many microstates the system can occupy under certain conditions
One of the key idea of entropy is that it disperses energy across the system
- We can actually quantify the distribution
We can use the statistical and thermodynamic definition of entropy to define the Boltzmann Distribution
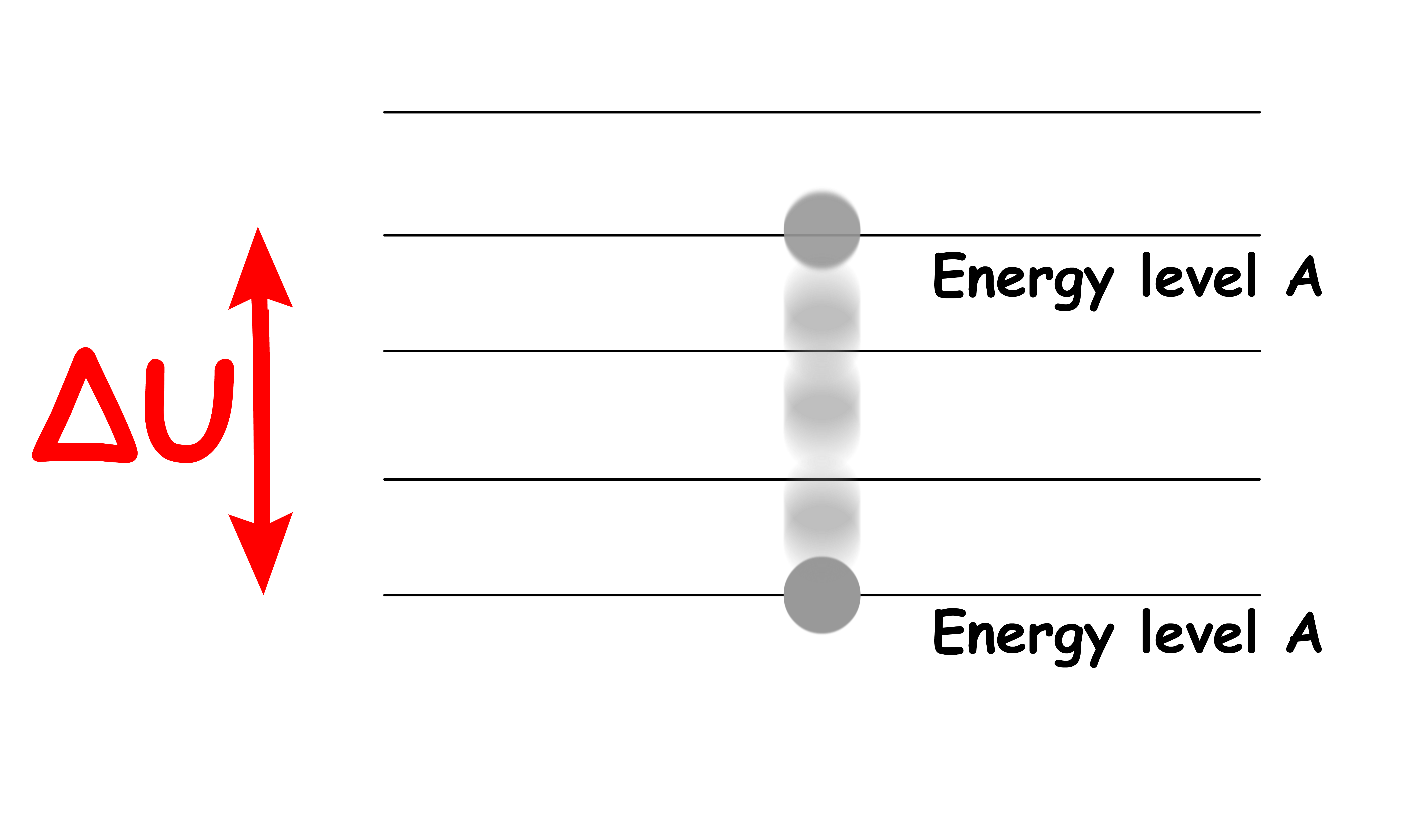
- Consider a system at constant volume, so no work is done. Therefore, energy can only be added in the form of heat
- Suppose the addition of heat promotes one particle to a higher energy level
- The population of the initial energy level will therefore decrease by 1, while the population of the final energy level will increase by 1
- Using the statistical definition of entropy change, we get
- We can rearrange the terms and simply it to get :
- Since the system has a constant volume, so no work is done. Hence,
- If we equate the two expressions for entropy change, we will get
- We can therefore express the ratio of population of the two energy levels as a function of the difference in energy and temperature