So far we have been using the internal energy to describe energy in a system
- This is actually quite limiting as it is only applicable to very specific situations
- In this chapter, we are going to design three more similar quantities that can cover virtually all situations
A thermodynamic potential, or more accurately, a thermodynamic potential energy is a state function used to represent the state of a system
- There are four thermodynamic potentials that we are concerned with here, internal energy ( U ), enthalpy ( H ), Helmholtz Energy ( A ) and Gibbs Energy ( G )
Thermodynamic potentials are very useful for the determination of equilibrium and spontaneity, or when measuring the properties of materials in a system
- Processes usually take place under some constraints, and when this is true, there is a corresponding thermodynamic potential that comes into play
Just as in classical physics, where potential energy is defined as capacity to do work, different thermodynamic potentials have different meanings when certain constraints are applied
Internal energy (U) is the capacity to do work plus the capacity to release heat
Enthalpy (H) is the capacity to do non-mechanical work plus the capacity to release heat
Helmholtz energy (A) is the capacity to do mechanical plus non-mechanical work
Gibbs energy (G) is the capacity to do non-mechanical work
- From these meanings, we can say that ΔU is the energy added to the system, ΔA is the total work done on it, ΔG is the non-mechanical work done on it, and ΔH is the sum of non-mechanical work done on the system and the heat given to it
¶ Enthalpy
Although the internal energy represents the total energy of a system, and the first law of thermodynamics is based on the concept of internal energy, it is not always the best variable to work with
- The change in internal energy is not equal to the heat flow when the system is free to change its volume
Enthalpy change ( ΔH ) is very useful because it can be related to the heat change in a system and this is really easy to measure
- Under certain specific situations enthalpy ( H ) is related to the heat change in a system and the effect can be measured easily by monitoring the temperature
¶ Origin of Enthalpy
One thing to bear in mind is that enthalpy by itself has no physical significance
- It is merely a state function we invented to allow us to make better measurements
Enthalpy is defined using internal energy
- The change of internal energy is given by the expression
- Since most chemical reaction will only do expansion work, so under constant pressure and assuming the process is reversible, the expression will become
- When taking measurements, the easiest one would be to observe the temperature change of the system, which occurs due to heat flow. Therefore, we should make the subject
- As the pressure is constant, we can add VdP to the right side of the equation without changing the equality
- The heat flow at constant pressure when only expansion work is performed is the differential of a state function, ( U + PV ). Therefore, it is also effectively a state function
- It is not only inconvenient, but extremely confusing if we use as a state function in most context, so we define a new state function, enthalpy, to make our lives a bit easier
¶ Defining Enthalpy
Formally, enthalpy is defined as
- Although enthalpy is derived using expansion work, the pressure term here is defined as the internal energy
There are two terms, the internal energy ( U ) and Pressure times Volume ( PV )
- The internal energy represents all the energy within the system
- The term Pressure times Volume is equal to the work required to push back the external pressure and create a space for the system to set in
One way to interpret enthalpy is that it describes all the energy the system possesses plus the energy required to make a space for our system to set in
The total enthalpy of a system cannot be measured directly, we most often refer to the change in enthalpy for a particular chemical reaction
- The equation can be rewritten the formula as such:
A change in enthalpy ( ΔH ) is related to:
- The work done due to a change in volume or pressure ( pext dV )
- The change in bonding / molecular interactions ( dU )
These changes are balanced by an exchange of heat with the surrounding
¶ Situations
Let us consider a situation where both the pressure and volume are constant
- When and
- Hence, the change in enthalpy is roughly the same as the change in internal energy at constant pressure and volume
- Since the volume is constant, there is no expansion work, so the change in internal energy is equal to the heat flow, \Delta U = q_
Let us consider a situation where the pressure is constant
- When the system is isobaric, , such that
- Hence, the change in enthalpy is given by
- If the only work done by the system is for expansion work, the change in internal energy is equal to sum of heat flow and the work done against the surrounding by the system
- Assuming only expansion work is done by the system, we can substitute work for pressure and volume
- Since the volume is not constant, the internal and external pressure should be equalized such that the two PV terms can cancel each other out
- At constant pressure, the enthalpy change ( ) is the heat exchange between the system and the surrounding
- The heat ( ) contributes to changing the internal energy of the system ( ) and doing compression / expansion work ( )
Let us consider a situation where the volume is constant
- Instead of expressing the change in enthalpy the usual way, we can substitute the term with using the perfect gas law
- The change in internal energy is equal to sum of heat flow and the work done against the surrounding by the system
- Under constant volume, there will be no expansion work done on or by the system
¶ The Free Energies
Entropy is the basic concept for discussing the direction of spontaneous change, but to use it we have to analyze changes in both the system and the surroundings
- This is because the 2nd Law is only applicable to isolated systems, so the process of determining the spontaneity of other systems requires us to determine both the internal and the external change in entropy
We can define equilibrium by finding the combined entropy change of the system and the surroundings
- Often it is more useful to have a definition for the position of equilibrium in terms of properties of just the system alone and which does not require a knowledge of changes taking place in the surrounding
A proper thermodynamic definition of a spontaneous process should take both energy and entropy changes into account
- We will introduce two new and similar state functions that do exactly that
We have seen that the Clausius inequality can show us whether a process is spontaneous, nonspontaneous or reversible
- The equality refers to a system undergoing a reversible change, or that the system is in equilibrium
- The inequality refers to the system undergoing a spontaneous and irreversible change
We can develop this inequality in two ways according to the conditions in which the process occurs: constant volume or constant pressure
- At constant volume and pressure, the heat exchange is the same as the change in internal energy and enthalpy respectively
- By setting these restrictions, we can show the criterion of spontaneous changes in terms of state functions only
We will see later how spontaneity can be indicated by state functions other than entropy
- It is important to bear in mind that these state functions are properties of the system, and they do not "technically" dictate the spontaneity of a process
- The only true determinant of spontaneity will always be entropy, it is just that we can use other state functions of the system to reflect the change in entropy of the surrounding, and thus determine the direction of a process indirectly
¶ From Entropy to Free Energy
Consider two changes, one at constant volume, and the other at constant pressure
- In the absence of any non-expansion work, we can say that and , such that
If we impose the restriction of constant internal energy ( ) or constant enthalpy ( ), the inequalities become
- In a system of constant volume and internal energy or constant pressure and enthalpy, spontaneous change is indicated by an increase in entropy
- They are consistent with our understanding of the 2nd Law
If we impose the restriction of constant entropy of the system ( dS = 0 ), since the temperature must be greater than 0, the inequalities then become
- In a system of constant volume or pressure and constant entropy, spontaneous change is indicated by a decrease in internal energy or enthalpy respectively
- Do not interpret this criterion as a system's tendency of the system to sink to a lower energy
- What it is saying is that if the entropy of the system is unchanged, then there must be an increase in entropy of the surrounding
- The increase in entropy of the surrounding can only be achieved if the internal energy or enthalpy of the system decreases as energy flows out as heat
Now that we know spontaneity can be indicated indirectly by the change in internal energy or the change in enthalpy, we can construct two new state functions
- We shall start with the Clausius inequality at constant volume or constant pressure
- We can rearrange the expression a bit to get
- We can then define the right side of the inequalities with a new state function, the Helmholtz Energy () and the Gibbs Energy ()
- Hence, we can say that a process is spontaneous when the change in Helmholtz energy or Gibbs energy is negative under constant temperature and volume or under constant temperature and pressure respectively
- Hence, we can say that a process is in equilibrium when the change in Helmholtz energy or Gibbs energy is zero under constant temperature and volume or under constant temperature and pressure respectively
The differential of Helmholtz energy at constant temperature and volume and Gibbs energy at constant temperature and pressure is expressed in terms of internal energy or enthalpy and entropy
- Since the temperature is not changing, we can add the term without affecting the equality
- We can therefore define the Helmholtz energy and Gibbs energy as such
¶ Interpretation of Free Energy through Work
We have already established that position of equilibrium can be defined the maximum work done by the system
- During a reversible change, the system perform maximum possible work
- We can define the free energy using maximum work
¶ Helmholtz Energy
From previous section, we have proven that reversible work can be expressed in terms of internal energy and entropy
- The right side of the equation is the same as the change in Helmholtz energy at constant temperature and volume
- This is a condition that must be satisfied by a reversible process
- Hence, at constant temperature and volume is a condition of equilibrium
- We can also say that the Helmholtz energy is a measure of the hypothetical maximum amount of work the system can perform on its surroundings
We can relate Helmholtz Energy with heat
- We have proven that , therefore
For a spontaneous change, both đw and dA will be negative, but đw will be less negative than dA
The work done by the system will be less than the decrease in A, thus only part of the system's change in free energy will be obtained as work
If a system is not harnessed to do work đw = 0, such that dA < 0, meaning dA is negative for a spontaneous process regardless of its nature
During a spontaneous process, the Helmholtz energy is decreasing
This will continue until the Helmholtz energy reaches the minimum value such that no further work can be obtained from the system even under reversible conditions
- We can therefore say that dA = 0 is the condition for equilibrium for a system at constant temperature and volume
- Spontaneous processes may occur in a system when it is not at equilibrium with a constant decrease in the free energy
- When the value of A is at its minimum, there will be no further decrease in Helmholtz energy ( ) and no further spontaneous changes can occur and the system is at equilibrium
¶ Gibbs Energy
- From previous section, we have proven that reversible work can be expressed in terms of internal energy and entropy
- We know that there are different types of work, so we can express the maximum total work in terms of maximum expansion work and maximum additional work
- If we rearrange the expression, we will get
- The right side of the equation is the same as the change in Gibbs energy at constant temperature and volume
- This is a condition that must be satisfied by a reversible process
- Hence, at constant temperature and pressure is a condition of equilibrium
- We can also say that the Gibbs energy is a measure of the hypothetical maximum amount of non-expansion work the system can perform on its surroundings
We can relate Gibbs Energy with heat
- We have proven that , therefore
For a spontaneous change, both and dG will be negative, but will be less negative than dG
The non-expansion work done by the system will be less than the decrease in G, thus only part of the system's change in free energy will be obtained as non-expansion work
If a system is not harnessed to do work = 0, such that dG < 0, meaning dG is negative for a spontaneous process regardless of its nature
During a spontaneous process, the Gibbs energy is decreasing
This will continue until the Gibbs energy reaches the minimum value such that no further work can be obtained from the system even under reversible conditions
- We can therefore say that dG = 0 is the condition for equilibrium for a system at constant temperature and pressure
- Spontaneous processes may occur in a system when it is not at equilibrium with a constant decrease in the free energy
- When the value of G is at its minimum, there will be no further decrease in Helmholtz energy ( ) and no further spontaneous changes can occur and the system is at equilibrium
¶ The Tax and Welfare of Free Energy
The "free" in free energy means that amount of energy available from some high potential source which can be directed into a work process and move the pieces about to get the work done
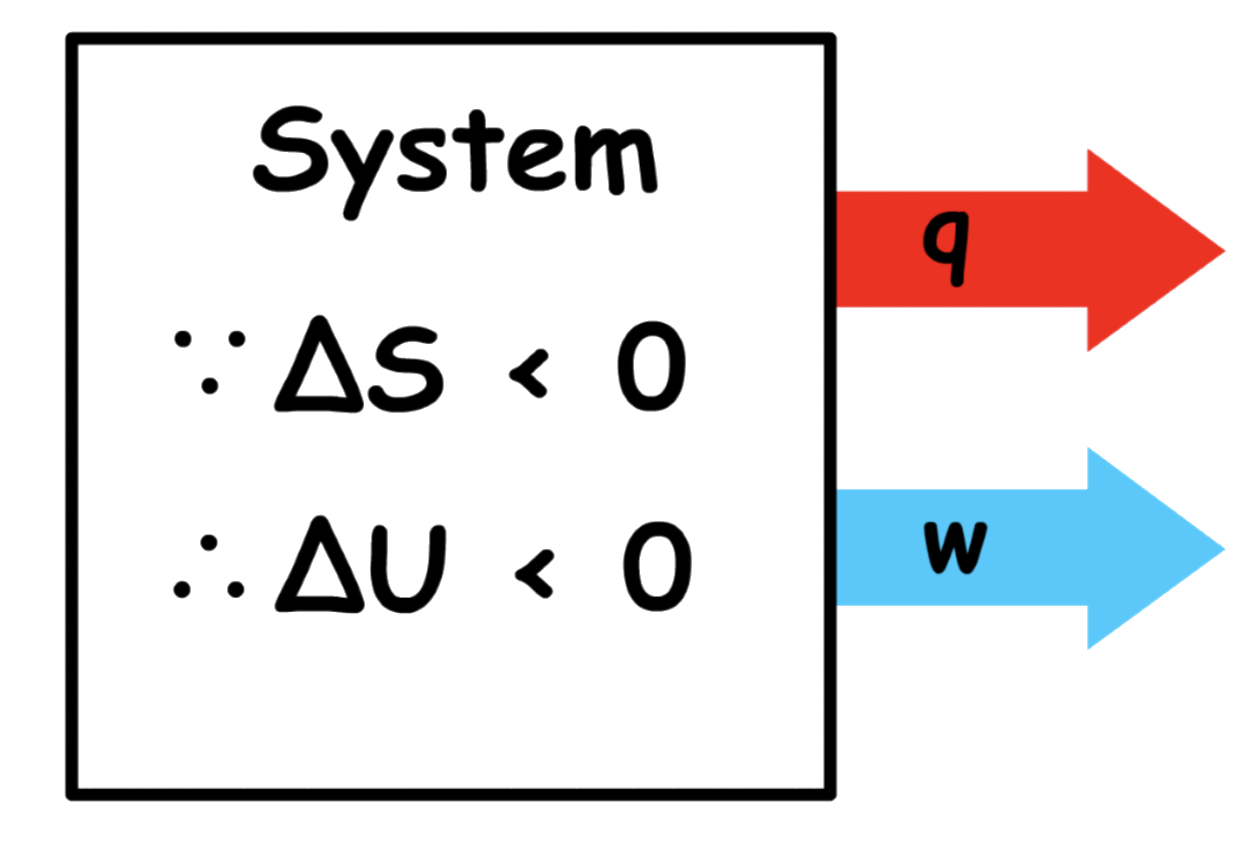
Let us consider a spontaneous process that brings about a decrease in entropy of the system
- Since the process is spontaneous,
- Since the entropy of the system is decreasing, is positive
- In order for to be negative, we need to make sure is not only negative, but large enough in magnitude to compensate for the decrease in entropy
- The change in Helmholtz energy is still negative, but it must be less negative than the change in internal energy
- We know that the change in Helmholtz energy is also the maximum possible work done by the system
- This means that the magnitude of change in internal energy is greater than the maximum possible work done by the system
- Since the decrease in internal energy cannot be covered by the work done of the system alone, the system must also lose heat to the surrounding
This is consistent with our narrative that the system needs to transfer heat to the surrounding to generate enough entropy in the surrounding to compensate for the decrease in entropy of the system
Not all the change in internal energy is used for the system to do work and some is lost to the surrounding as heat
Nature is demanding a tax on the internal energy such that part of ΔU is transferred to the surrounding as heat ( The tax ) and the rest can be transferred to the surrounding as work ( The free energy )
is the part of that we are free to use to do work
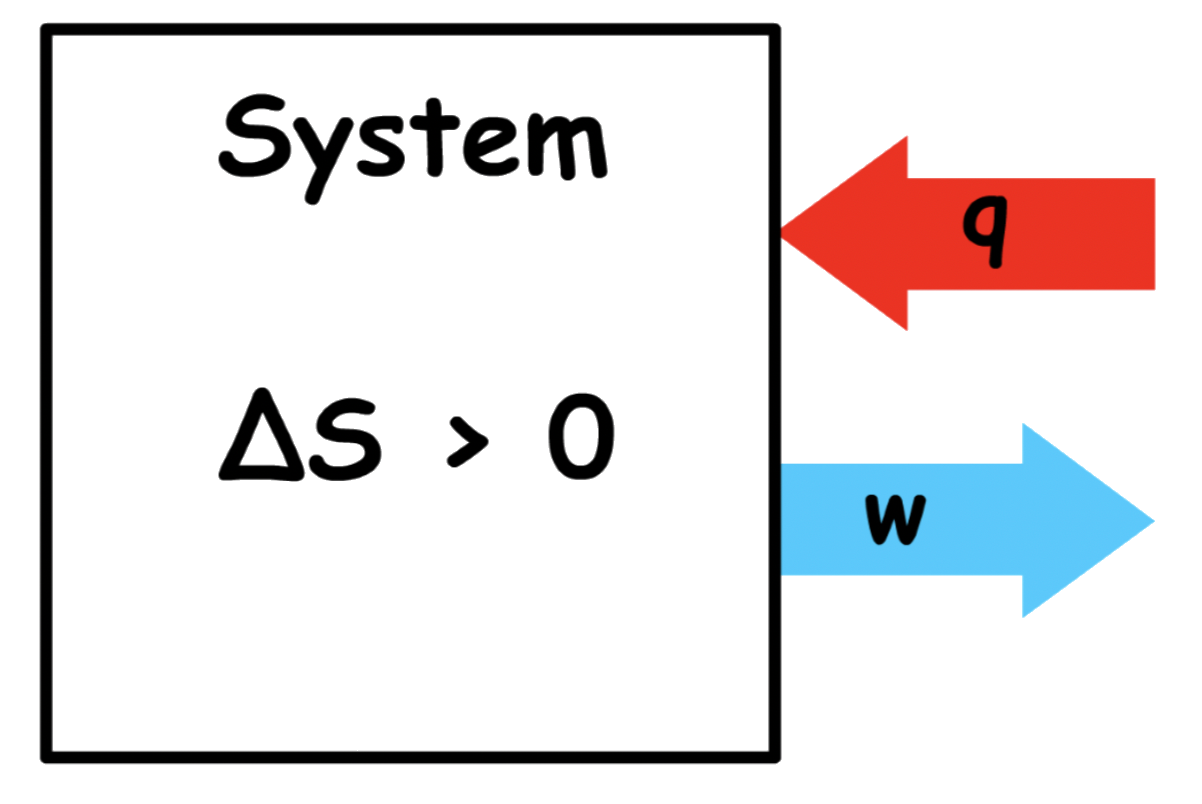
Let us consider a spontaneous process that brings about an increase in entropy of the system
- Since the process is spontaneous,
- Since the entropy of the system is increasing, is negative
- As long as is not a positive number that is greater than in magnitude, the value of can be positive or negative. Whether is positive or negative has no effect in this discussion
- The change in Helmholtz energy is negative, and it must be more negative than the change in internal energy
- We know that the change in Helmholtz energy is also the maximum possible work done by the system
- This means that the magnitude of change in internal energy is smaller than the maximum possible work done by the system
Since the of change in internal energy is not enough to cover all the work done by the system, at least some of the energy of the work must come from outside the system in the form of heat
- If is positive, not only is the system unable to cover any of the energy required for the work done by the system, the system needs external energy supplied in the form of heat. Hence, in this case, the heat gained by the system will be large
- If is negative, the system can only cover a portion of the energy required for the work done by the system. The rest of the required energy will have to be provided from outside in the form of heat. Hence, in this case, the heat gained by the system is relatively small
Overall, the change will look something like this
- The change in internal energy is unable to pay for all, if any, of the energy required for the work done by the system. As a result, energy may flow into the system as heat as work is being done by the system
- Nature is now giving a tax refund to the system such that at least part of the work done by the system is compensated by the heat flow from the surrounding( The tax refund ). Depending on how positive ΔU ( how poor the system is ), the tax refund may be larger