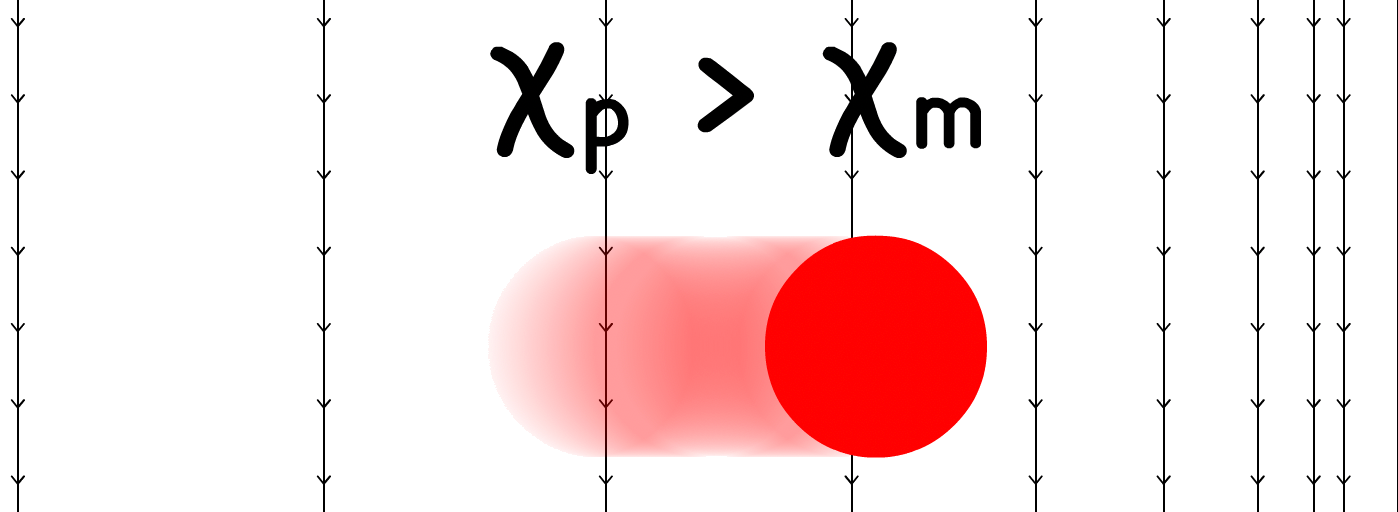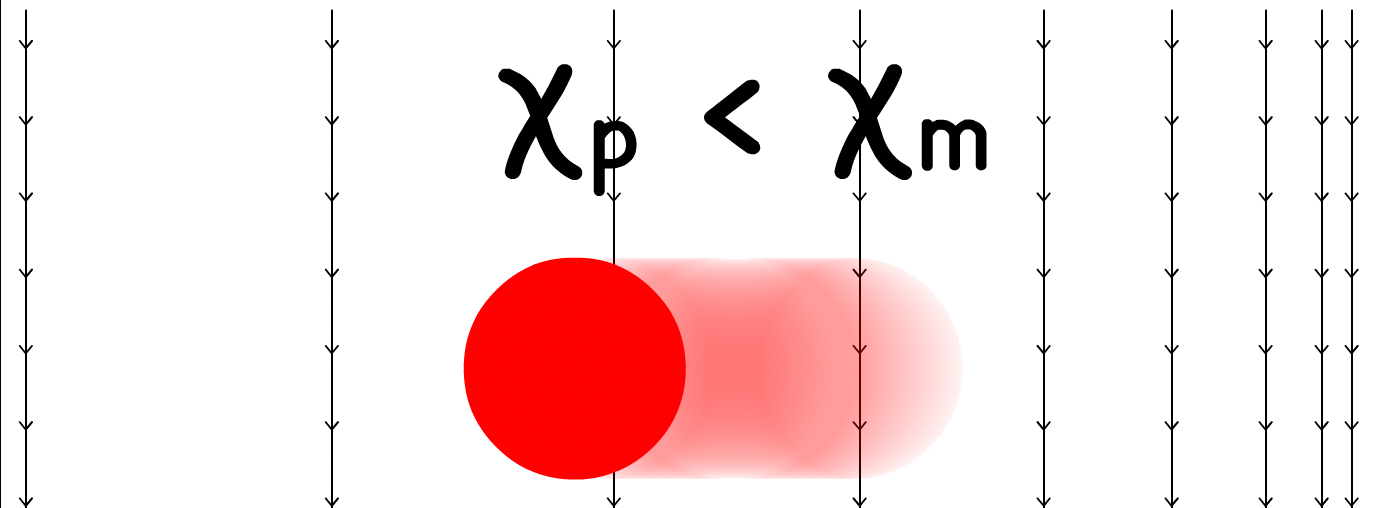Transport properties are essential to understand the behavior of matter and energy in various materials and systems
- These properties refer to the ability of matter or energy to move through a non-uniform medium, which may include fluids, solids, and gases
- In general, transport properties are influenced by the microscopic structure and composition of a material
We will mainly focus on the following transport properties
1. Diffusivity
2. Electrical Conductivity ( discussed in the previous chapter )
3. Thermal Conductivity
4. Magnetophoresis
¶ Flux ( J )
The rate of migration of a property is measured by its flux ( )
- We define flux as the quantity of said property passing through an imaginary plane per unit area per unit time
- If the property is matter, we speak of a matter flux. If the property is energy, we speak of an energy flux
We can use flux to compute other quantities
- The rate of migration of a property can be found by multiplying the flux with the cross-sectional area , , of the imaginary plane said property is passing through
- The total quantity of a property transferred through a given area in a given time interval is given by the product of the flux, area and the time interval
¶ Disffusion
Diffusion is the macroscopic motion of components within a system that occurs due to the presence of a concentration gradient
- Diffusion results in the passage of particles from one part of the system to another while maintaining a constant total pressure
¶ Fick's First Law of Diffusion
Let's suppose we have a system of two components, separated by a removable impermeable partition
- When the partition is removed, the components from the two chamber will mix together
Fick's First Law of Diffusion governs the rate of diffusion
The driving force for diffusion at any time is the concentration gradient along the diffusion direction ( x-axis ). Moreover, the rate of diffusion is directly proportional to the area of the plane that is perpendicular to the diffusion direction
- The diffusion direction is that in which the concentration decreases ( i.e. is negative)
- As time goes on, the at a given plane changes, eventually dropping to zero. At that point, diffusion stops
This proportionality can be written as an equality by the introduction of the proportionality constant
- The negative sign allows , the diffusion constant to take on positive values
- The value of depends on the nature of both the diffusing solute and the solvent, the temperature and pressure
Alternatively, we can express the law in terms of flux
- A positive value of J signifies a flux towards the positive x-axis
- A negative value of J signifies a flux towards the negative x-axis
¶ Understanding Fick's First Law from a Thermodynamic Perspective
Understanding Fick's First Law from a thermodynamic perspective reveals its relationship to the second law of thermodynamics
- Diffusion of a substance from high to low concentration is a spontaneous process that leads to increased entropy
Chemical potential is used instead of concentration gradient to quantitatively describe diffusion in order to speak in the language of thermodynamics
- Diffusion occurs as a result of a gradient in the chemical potential
- If the chemical potential for a species is uniform in a system, there is no driving force for diffusion
Work done and Diffusion
We are interested in knowing the work needed to move one mole of substance from one location to another
From Year 1 notes, we should know that the maximum non-expansion work is just the change in Gibbs energy at constant temperature and pressure. Moreover, since we are discussing in units of one mole, we can use chemical potential instead
- In a system in which chemical potential depends on the position x
- Recall that the formal definition of work is expressed in terms of a force. Equating these two expressions for work, we will be able to relate the change in chemical potential with a force
- Although this force is illusionary, it provides an interesting and useful approach to discussing diffusion
- The driving force here is defined to be the force required to move one mole of substance
Diffusion in Ideal Solutions
As chemistrs, we are especially interested in diffusion happening in solution
- The chemical potential of an ideal solution can be written as . (We are allowed to use concentration here instead of mole fraction, but they will have different value of )
- The frictional force is given by ( discussed in the previous chapter ) and it is equal to the driving force of diffusion on one particle
- Flux is nothing but the rate of tranport per area, so the product of the drift speed and concentration is just flux ( )
- By comparing this expression to Fick's First Law, we will be able to find an expression for the diffusion coefficient
- Measurement of in a solvent of known viscosity therefore permits a value of (hydrodynamic radius) to be calculated
¶ Relating Diffusion and Electrical Conductivity
We can also express the drift speed in terms of the diffusion coefficient
- Let us return to Fick's First Law and recall that the flux can be expressed as the product of the drift speed and concentration
- The thermodynamic interpretation of diffusion allows us to relate the concentration gradient with an illusionary driving force
- We can then substitute it into the equation and perform some algebaric manipulation
- This equation allows us to calculate the drift speed of molecules regardless of the origin of the driving force
Having obtained a relation between drift speed and driving force, we can apply it in scenarios where the driving force is the electric force acting on ions when conducting electricity
- From the previous chapter, we know that drift speed of ions is also related to ionic mobility and electric field strength. We can therefore combine these two relations
- in the situation of electrical conductivity, the driving force is the Columbic force, which is given as the product of the charge of the ion and the electric field . However, recall that the driving force here is defined for one mole of substance, so
- The charge of one ion is given by the product of the charge number and the magnitude of the charge of an electron ()
- Since and , there are two alternative ways to express the Einstein Relation
In the previous chapter, we have also established a relation between ionic mobility () and molar conductivity (). Now that we have connected with the , we can also relate with
- The relation between ionic mobility () and molar conductivity () is given by
- We can substitute in Einstein relation for
- Note that doesn’t depend on charge since diffusion is not driven by charge effects
¶ Fick's Second Law of Diffusion
We shall now turn our attention to the discussion to the time evolution of the concentration profile of a substance undergoing diffusion
- In studying transport processes, the flux is rarely measured directly. What is measured is the rate of change in concentration with respect to time at various points
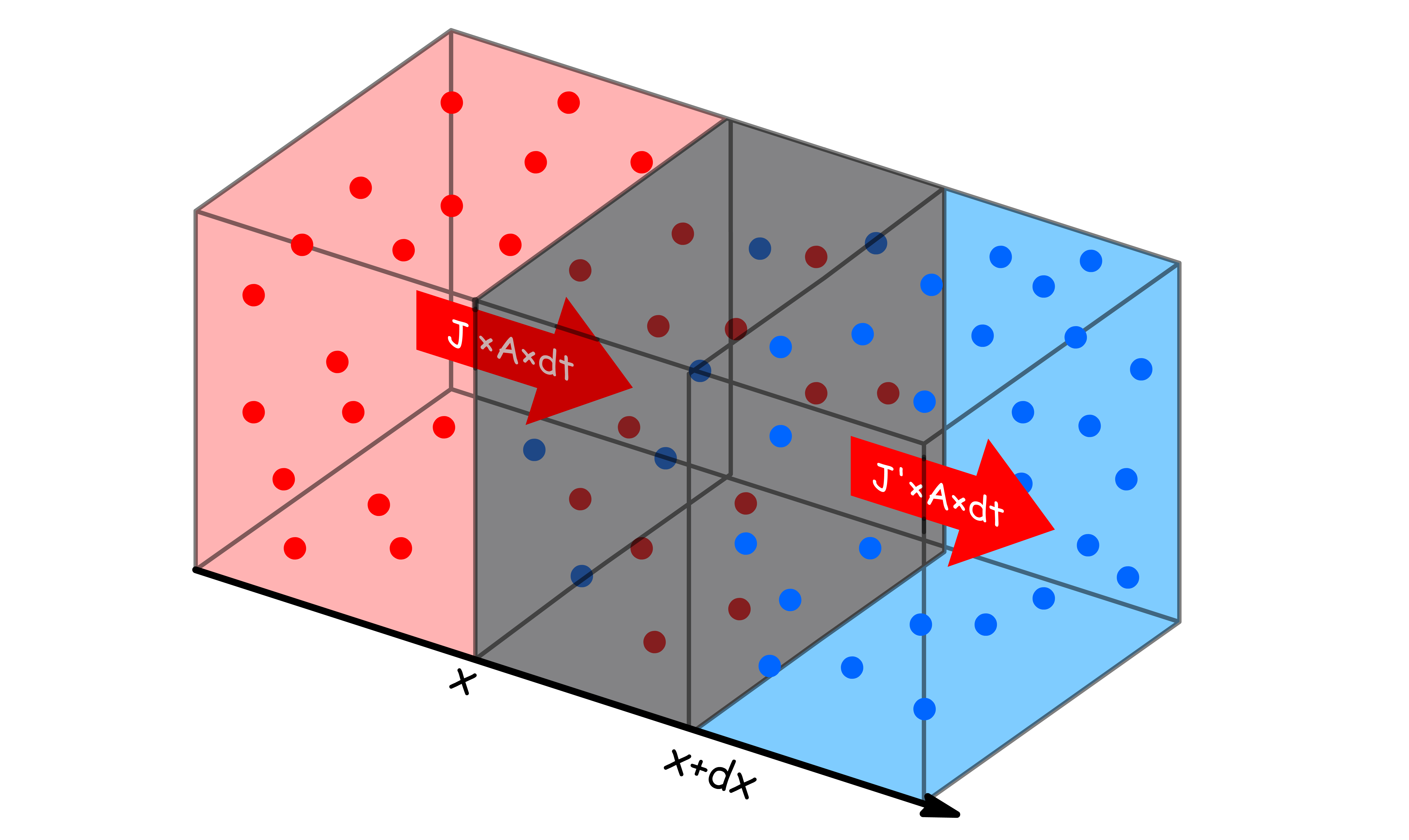
The Continuity Equation
To simplify matter, we shall first consider the time-dependency of concentration of a region before going straight to a point
- The region stretches from to
- The concentration at position and are and respectively
- THe flux at position and are and respectively
Recall that our objective here is to find an expression for the net rate of change in concentration with time
- The net gain in quantity of substance in the region is related to the quantity of substance entering the region at and the quantity of substance leaving at
- We can express the rates of changes with the fluxes at the respect positions
- We can express in terms of as such:
- The net gain in substance in the region can be expressed as the change in concentration multiplied by the volume of the region
- Simply by rearranging the equation, we will arrive at an expression for the net rate of change in concentration with time
- This is referred to as the equation of continuity and it relates the time-dependence of concentration at a given value of x in the cell to the rate of change of flux with distance
Fick's Second Law
To go from the continuity equation to Fick's Second Law, we simply have to substitute in Fick's First Law ( ) for the flux
¶ Nature Abhors Wrinkles
The second law can therefore be regraded as a mathematical formulation of the intuitive notion that there is a natural tendency for concentration of a system to even out
- When the curvature is positive ( when there is a dip ) , the change in curvature is positive ( the dip tends to be filled )
- When the curvature is negative ( when there is a heap ) , the change in curvature is positive ( the heap tends to spread out )
When the curvature is zero ( linear ), then the concentration is constant in time
- Even when the concentration is increasing or decreasing, as long as it is linear, the concentration will be independent of time
- This is because the inflow of particles is exactly balanced by the outflow
¶ Diffusion with Convection
Convection refers to the bulk movement of fluid, as opposed to the individual movement of molecules in diffusion
- While Fick's Second Law describes the diffusion of substances, it is only applicable in the absence of convection.
- When diffusion and convection occur together, the concentration of a substance at any given point is governed by the generalized diffusion equation, which takes into account both diffusion and convection
- Here, is the diffusion coefficient, is the fluid velocity, and is the concentration of the substance at a given point in space and time
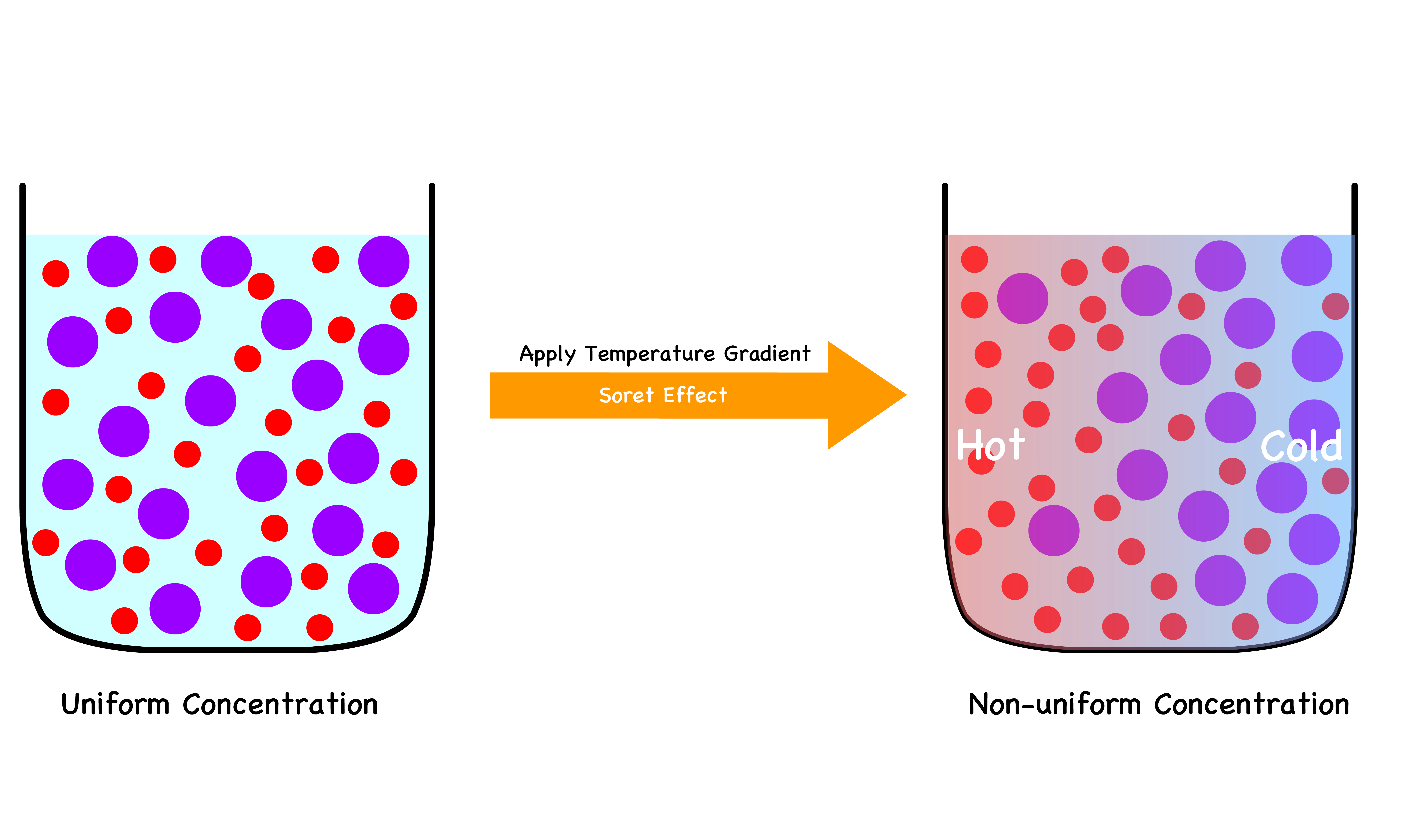
¶ Thermophoresis
Thermophoresis refers to the movement of particles in the presence of a temperature gradient
- Thermophoresis has the capability to induce a transition in solute concentration from a state of uniformity to one of non-uniformity
- It is driven by differences in temperature across the system, which cause thermal gradients that induce particle movement
- The temperature gradient, , generates an effective “thermal forces,” although no “real” external field is present
¶ The Thermophoretic Drift Velocity
The thermophoretic drift velocity describes the motion of a particle in response to a temperature gradient
- When a particle is exposed to a temperature gradient, its molecules experience a different thermal energy on one side compared to the other
- This leads to a difference in the rates of collisions between the particle and the surrounding fluid molecules on each side, which generates a net "force" that drives the particle in the direction of the colder region
- This "force" is called the thermophoretic force, and it acts in a direction opposite to the temperature gradient
- This thermophoretic force should be thought of as the force that needs to be exerted on the particle to cancel out its thermophoretic drift velocity
The thermophoretic drift velocity can be expressed in terms of the temperature gradient
- This equation indicates that the thermophoretic drift velocity is proportional to the temperature gradient and is directed towards the colder region
- The minus sign indicates that the thermophoretic force acts in the opposite direction to the temperature gradient
Alternatively, the thermophoretic drift velocity can be expressed as two different temperatures
The magnitude of the thermophoretic force is proportional to the thermal gradient and is determined by the thermal diffusion coefficient, which is a measure of the ability of a fluid to conduct heat
- This coefficient depends on the properties of the fluid, such as its viscosity, thermal conductivity, and specific heat capacity
- The thermal diffusion coefficient is usually much smaller than the diffusion coefficient that governs the ordinary Brownian motion of particles, which means that thermophoretic motion is typically slower than diffusion
¶ The Ludwig–Soret effect
The Phenomenon
The Soret effect, also known as thermal diffusion or thermal diffusion effect, describes the occurrence of a concentration gradient within a mixture of two or more substances resulting from a temperature gradient
- When a mixture of has a temperature gradient, the heaveir components tend to diffuse towards the colder region while the lighter components move towards the hotter region
- The molecular weight and size of a substance affect its diffusivity because larger molecules tend to move more slowly through a medium, while smaller molecules move more quickly
- When a mixture is subjected to a temperature gradient, the hotter region of the mixture has a higher kinetic energy, which increases the molecular motion and results in a higher diffusivity of the lighter components. As a result, they move more quickly through the mixture and accumulate in the hotter region
- Conversely, the colder region of the mixture has a lower kinetic energy and results in a lower diffusivity of the heavier components. As a result, they move more slowly through the mixture and accumulate in the colder region
Maths
In order to understand the combined effect of thermophoresis and diffusion, we can consider the total flux of particles in the fluid, which is the sum of the thermal flux and the mass flux
- The thermal flux is the flux of particles driven by the thermophoretic force, and can be written as the product of the concentration of particles and v_T is the thermophoretic drift velocity
- The mass flux is the flux of particles due to diffusion, and it is given by Fick's law in terms of the concentration gradient
The total flux, denoted by J, is the sum of the thermal and mass fluxes
- In one dimension, where the temperature and concentration gradients vary only in the x-direction, the respective gradients are just the corresponding derivatives with respect to
- This equation describes the combined effect of thermophoresis and diffusion on the transport of particles in the fluid
- The first term on the right-hand side represents the flux of particles due to the thermophoretic force, and the second term represents the flux of particles due to diffusion.
In a closed system in steady state, the total flux of particles is zero, which means that the flux due to thermophoresis is balanced by the flux due to diffusion
- This condition leads to a relationship between the temperature and concentration profiles in the fluid
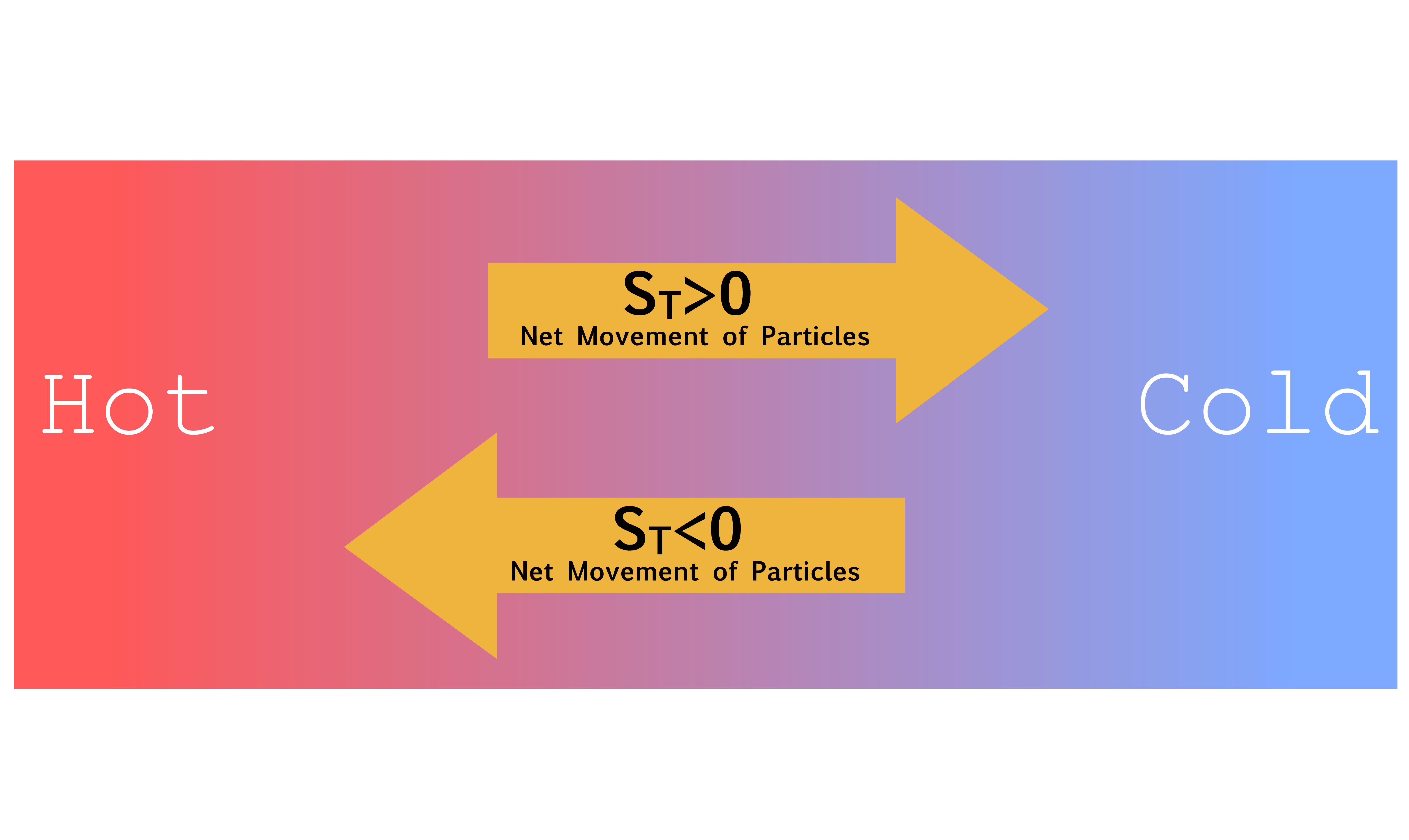
- In particular, for a closed cell with two different temperatures and , the concentration ratio of particles at the two temperatures is given by
- For the sake of simplicity, we define the Soret coefficient as \frac{D_T}
- This relationship allows us to quantify the effect of thermophoresis on the concentration distribution of particles in a fluid
The Soret coefficient is an important parameter in thermophoresis, as it characterizes the strength of the thermophoretic effect relative to the diffusion process
- A positive Soret coefficient indicates that the particles tend to move towards the colder region of the system, while a negative Soret coefficient implies the opposite
- The Soret coefficient can be affected by a variety of factors, such as the size and shape of the particles, their surface properties (such as charge and hydrophobicity), and the composition of the surrounding medium
The Seebeck effect is another phenomenon that can influence thermophoresis
- It arises due to the movement of ions in the buffer along a thermal gradient, which generates an electric field that can induce electrophoretic movement of the particles
- The Seebeck effect can also cause the Soret coefficient to change sign, as the electric field generated by the thermal gradient can either enhance or counteract the thermophoretic drift
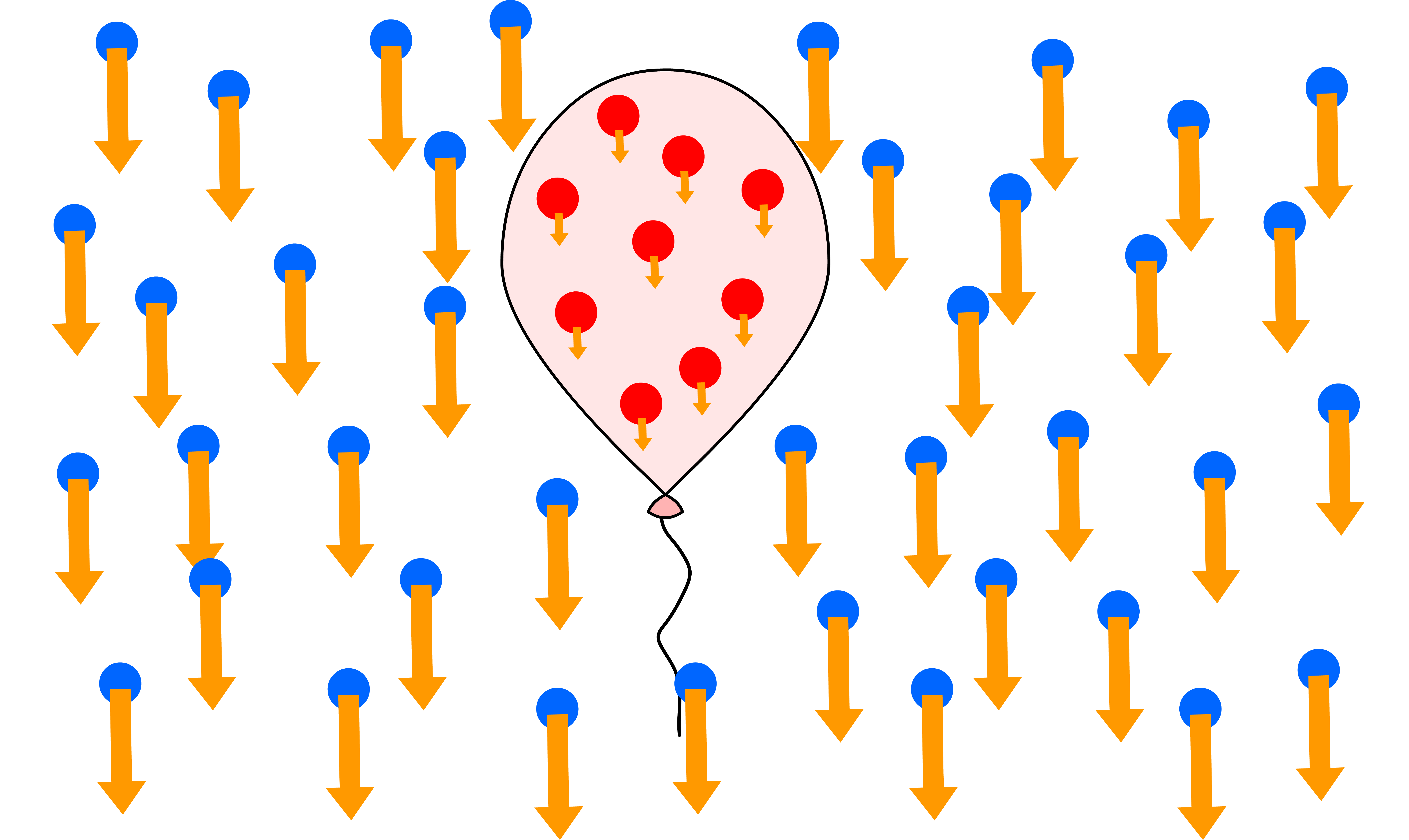
¶ Magnetophoresis
Magnetophoresis is a phenomenon where particles migrate in a magnetic field
- This migration can occur in a gradient of magnetic field, a gradient of magnetization of the surrounding medium, or a combination of both
A material's magnetization, , represents the extent to which a material can be magnetized under an external magnetic field
- It is defined as the magnetic moment per unit volume of the material
- The magnetic moment, which is a property of every atom and molecule, arises from the motion of electrons around the nucleus
- When an external magnetic field H is applied to a material, it induces a magnetic moment in the electrons of the material, causing them to align their spins and orbital motions with the field
The magnitude of the magnetic moment of a material is proportional to the strength of the external magnetic field, as well as the number of unpaired electrons in the material
- The higher the number of unpaired electrons, the higher the magnetic moment
- In addition, the magnetic moment of a material is also influenced by the temperature of the material. At higher temperatures, the thermal energy can overcome the magnetic interactions, causing the magnetic moment to decrease.
We want a parameter that tells us the intrinsic property of a material in response to an external magnetic field
- Magnetization is not a good candidate because it depends on the external magnetic field
- We therefore need to define a new quantity, , the Magnetic Susceptibility
¶ Magnetic Susceptibility ( χ )
The magnetic susceptibility of a material, denoted by , is a dimensionless quantity that describes the degree to which a material can be magnetized in an external magnetic field
- It is defined as the ratio of the material's magnetization M to the applied magnetic field strength H:
- The magnetic susceptibility provides a measure of the intrinsic magnetic property of the material, as it is independent of the strength of the external magnetic field
We can put materials into three different catagories base on their value of magnetic susceptibility
Ferromagnetic
Ferromagnetic materials are characterized by a large positive magnetic susceptibility
- They exhibit a strong magnetization even in the absence of an external magnetic field
- Ferromagnetic materials have unpaired electrons, and the thermal fluctuations are small compared to the forces that lead magnetic dipoles to lock in orientation aligned with H
- The result is a strong and permanent magnetization, which makes ferromagnetic materials useful for various applications
Paramagnetic
Paramagnetic materials have a positive magnetic susceptibility but weaker than ferromagnetic materials
- Paramagnetic materials have unpaired electrons, and the spins of the unpaired electrons align with to produce a magnetic moment
- Paramagnetism is manifested when thermal fluctuations prevent the magnetic dipoles from locking in orientation aligned with the field
- Susceptibility decreases with increasing temperature because the thermal motion randomizes the spin orientations and is the basis of the Curie law
Diamagnetic
Diamagnetic materials have a negative magnetic susceptibility
- Diamagnetic materials have all electrons paired
- The diamagnetic effect stems from changes in electron orbital motion induced by a and leads to dipoles aligned against (opposing)
- Diamagnetism is generally weaker than paramagnetism, but it is still a significant effect in many materials
¶ Magnetophoresis Mechanism
In magnetophoresis, the mobility of the particle depends on the mismatch between the magnetic susceptibility of the particle and the medium , and the gradient of the magnetic field
- When > , positive magnetophoresis occurs, and the particle migrates towards the stronger magnetic field ( denser field lines )
- In contrast, when < , negative magnetophoresis occurs, and the particle migrates towards the weaker magnetic field ( less dense field lines )
The gradient of the magnetic field provides a force that pulls the particles in the direction of the field's increasing strength
- The gradient affects the magnitude of the mobility, but not the direction
An Appeal to Intuition
To understand why the direction of travel of the particle depends on the relative size of the magnetic susecptibility between the object and the medium, let us take a detour and understand whether an object float or sink depends on the relative density of the object and the medium
- All objects on Earth are pulled downward by the gravitational force
- Objects with higher density contain more mass per unit volume, so they experience a stronger gravitational force than objects with lower density
- As a result, the denser object will sink or go down more than the less dense object. This creates the illusion that the less dense object is floating, when in reality it is being pushed up by a force equal to the weight of the fluid it displaces
- Therefore, it's not that the less dense object is floating, but rather, it is being supported by a buoyant force that is equal to the weight of the fluid it displaces
Similarly, in magnetophoresis, the direction of travel of the particle depends on the relative size of the magnetic susceptibility between the object and the medium
- Objects with higher magnetic susceptibility experience a stronger magnetic force than those with lower magnetic susceptibility when subjected to a magnetic field gradient
- As a result, the particles with higher magnetic susceptibility will move towards the stronger magnetic field, while particles with lower magnetic susceptibility will move towards the weaker magnetic field
- This creates the illusion that the less magnetic particle is "floating" in the magnetic field gradient, when in reality it is being pushed by a force that depends on the difference in magnetic susceptibility between the particle and the medium
- Therefore, it's not that the less magnetic particle is floating, but rather, it is being affected by a magnetic force that is dependent on the difference in magnetic susceptibility between the particle and the medium
¶ Transport through Advection
Transport through advection is an important mechanism for chemical species transport, particularly when the diffusion and migration rates are too slow, especially in larger systems
- Advection is the transport of a substance by bulk motion of the fluid which contains it ( Some textbooks define this process as convection, but “convection” is often considered to be the case where advection and diffusion occur )
- It is typically caused by differences in pressure, density or mechanical movement of an object
- Advection is characterized by the velocity of the fluid, and the characteristic transport time is given by , where is the velocity and is the length
Advection is typically caused by differences in
- Pressure (gravity induced, externally applied etc)
- Density (e.g. due to heating)
- Mechanical movement of an object (e.g. stirrer)
¶ Dimensionless Number
Dimensionless numbers are used to establish the predominance of different effects in advection
- Typically the ratio of two sets of physical parameters to determine which is greater
- Used to establish the importance of different effects
- The Sherwood number relates which process dominates, comparing diffusion to advection
- A high Sherwood number indicates that advection dominates, while a low Sherwood number indicates that diffusion dominates
¶ Laminar versus turbulent flow
Laminar flow is characterized by fluid following along smooth paths in layers
- each layer moving smoothly past the adjacent layers with little or no mixing
- It is easier to describe mathematically and is more energetically efficient
- It is less efficient at mixing
Turbulent flow is chaotic
- There are cross-currents perpendicular to the direction of flow, eddies and swirls
Laminar versus turbulent flow can also be characterized by the dimensionless Reynolds number
It is the balance between inertia and viscosity
- The different regimes can be characterised by the dimensionless Reynolds number
¶ Shear
Shear is an important concept in advection, as it can create a shear stress which affects the velocity of the fluid
- Shear stress is defined as
- is the force parallel to the surface, and is the area of the surface
- For laminar flow, this leads to a parabolic velocity profile, while for turbulent flow, it is more complex, but there remains a laminar region adjacent to the interface