¶ Phenomenons in Electrolytic Solutions
Before we begin our discussion on electrolytic solutions, we shall first gain some basic understanding of columbic interaction
- The force exerted by one point charge on another is given as such
The nature of the force depends on the relative sign of the charges
- If the sign of the point charges are different, the force will be attractive
- If the sign of the point charges are the same, the force will be repulsive
The attractive force between ions of opposite charge is greater :
- for higher charges
- in solvents of low dielectric constant (εr)
- when ions are close together (effect of r)
Electrolytic solutions contain ions that can interact with each other and with the solvent molecules. There are several interesting and important phenomena associated with electrolytic solutions
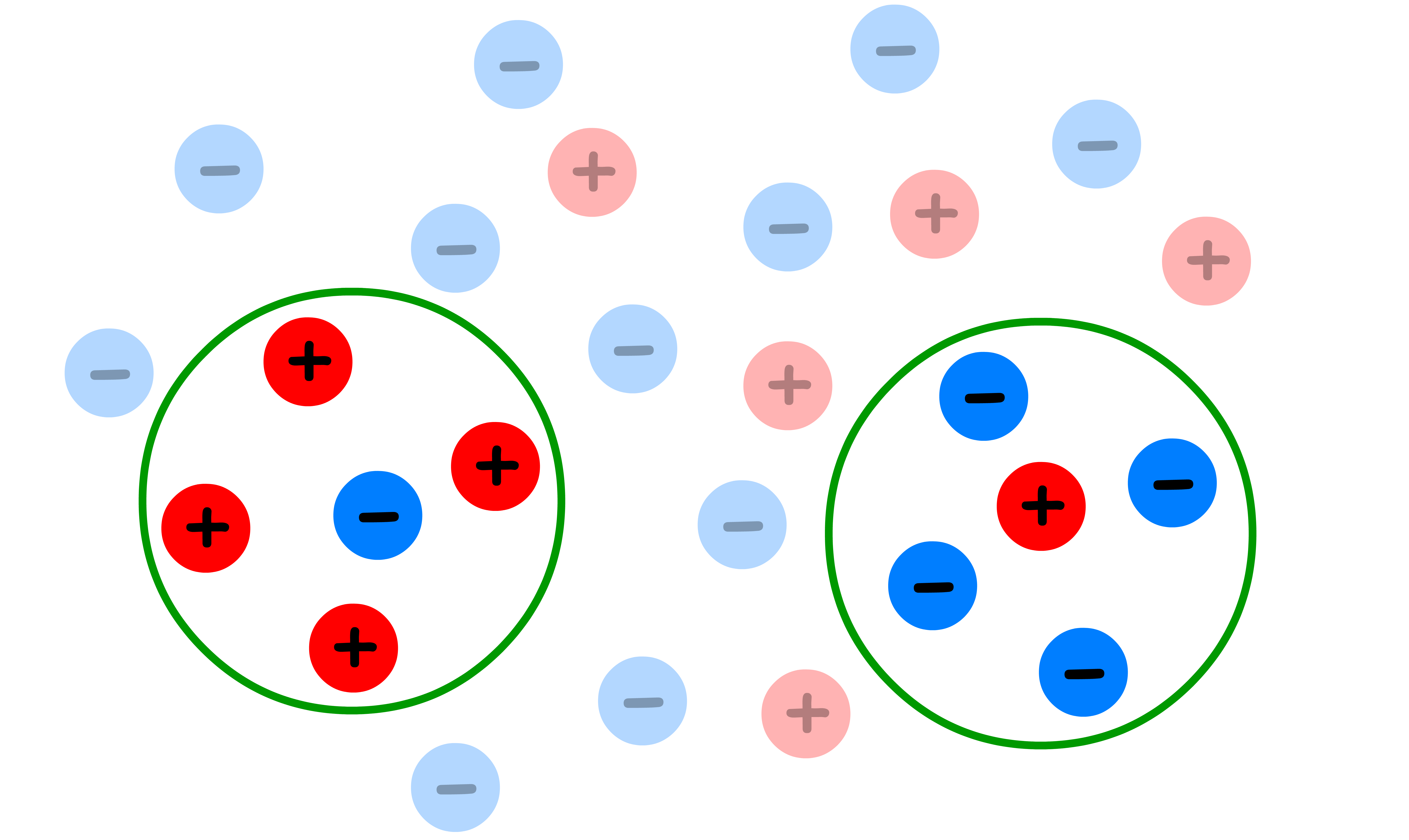
1. Ionic atmosphere
- Ion-ion interaction
- Describes the cloud of counterions surrounding each ion
2. Ion pairs
- Ion-ion interaction
- Form when oppositely charged ions come into close proximity
3. Ion-solvent interactions
- Ion-solvent interaction
- Play a crucial role in determining the solubility and behavior of ions in solution
¶ Ionic Atmosphere
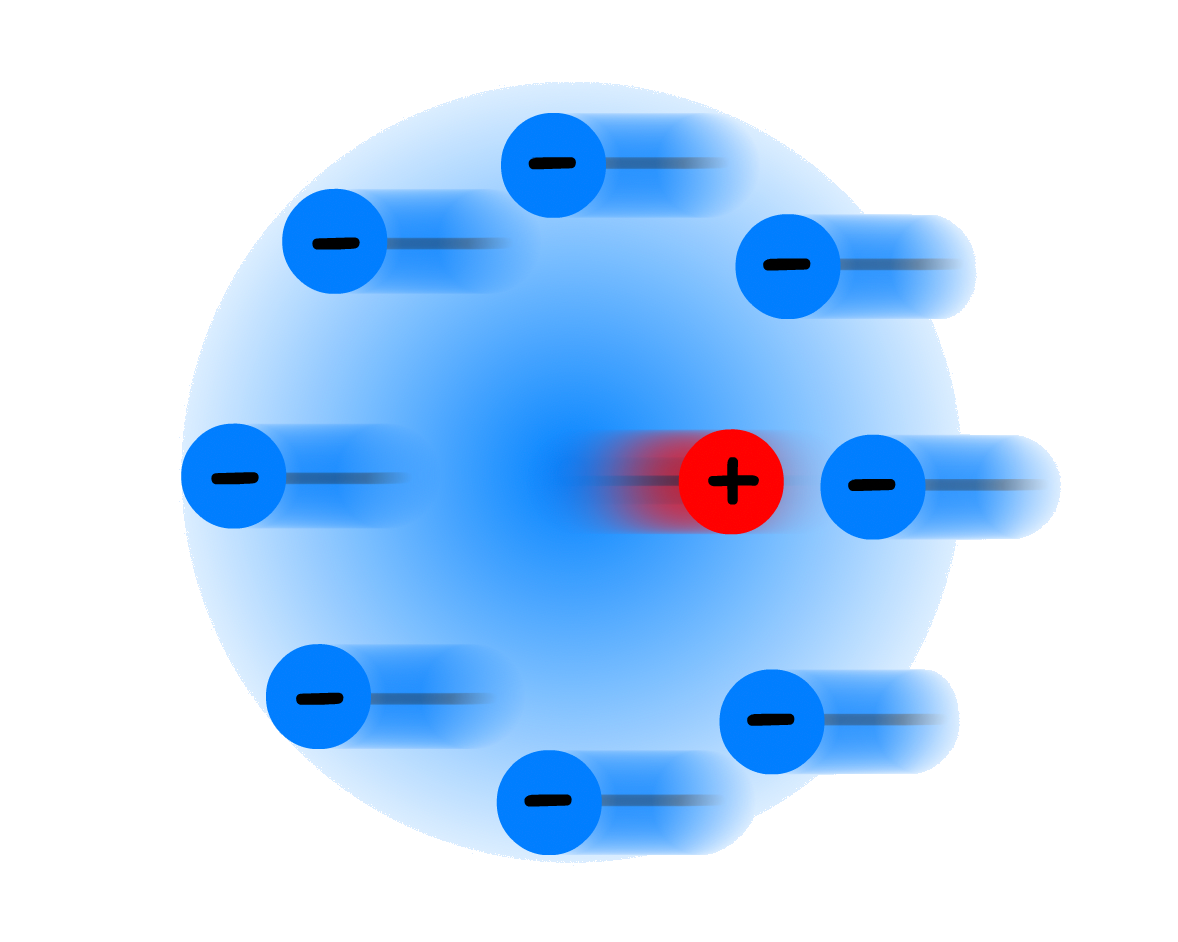
In spite of the thermodynamic drive towards a randomized distribution of ions in electrolytic solutions, electrolytic solutions do not exhibit completely random arrangements of ions
- In the near neighbourhood of each ion, there are more ions of the opposite charge than of the same charge (does not include solvent)
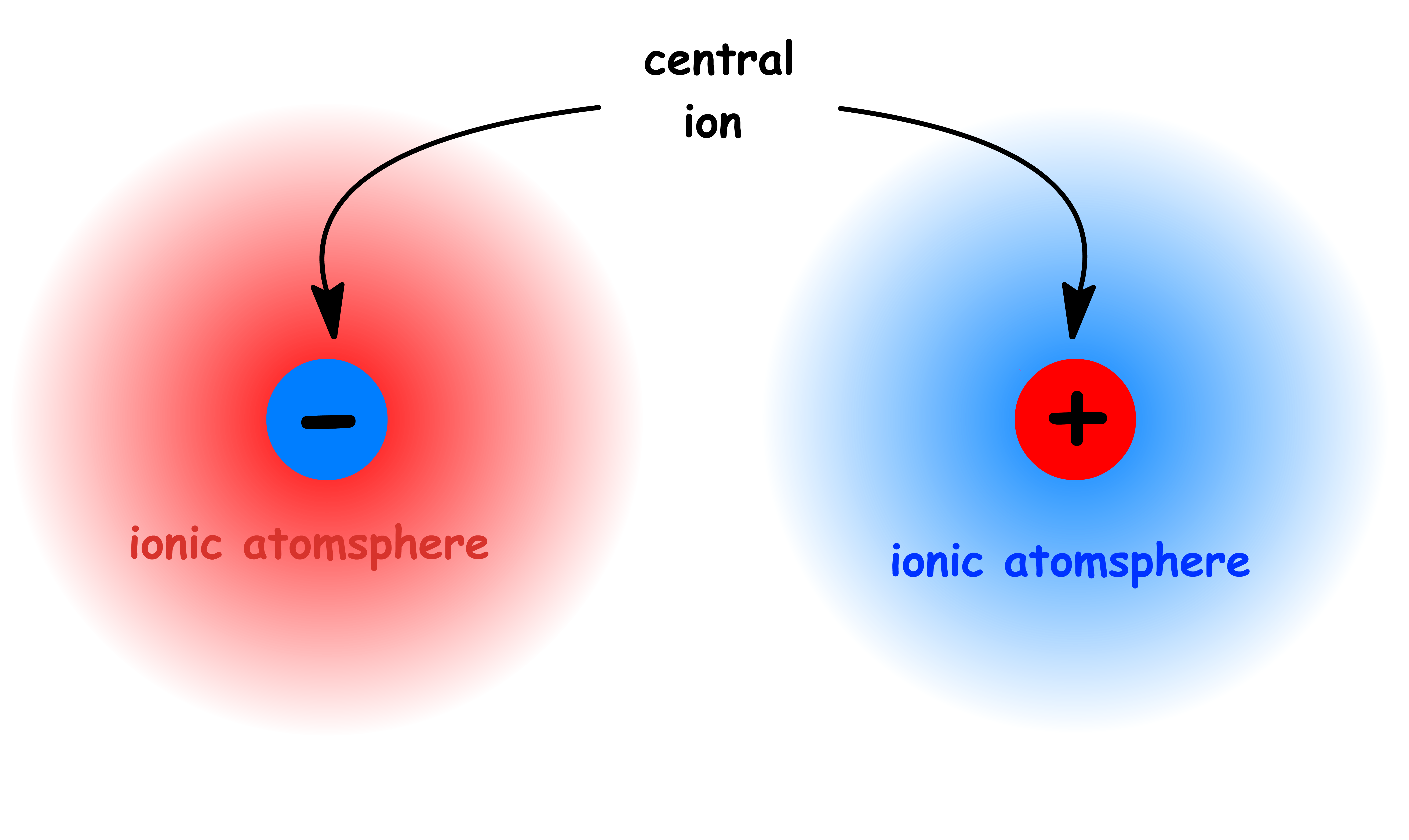
- An ionic atmosphere, which is a diffuse cloud of ions with opposite charge surrounding a central ion, is a convenient way of describing the phenomenon.
- The ionic atomsphere has a total charge equal and opposite to the central ion
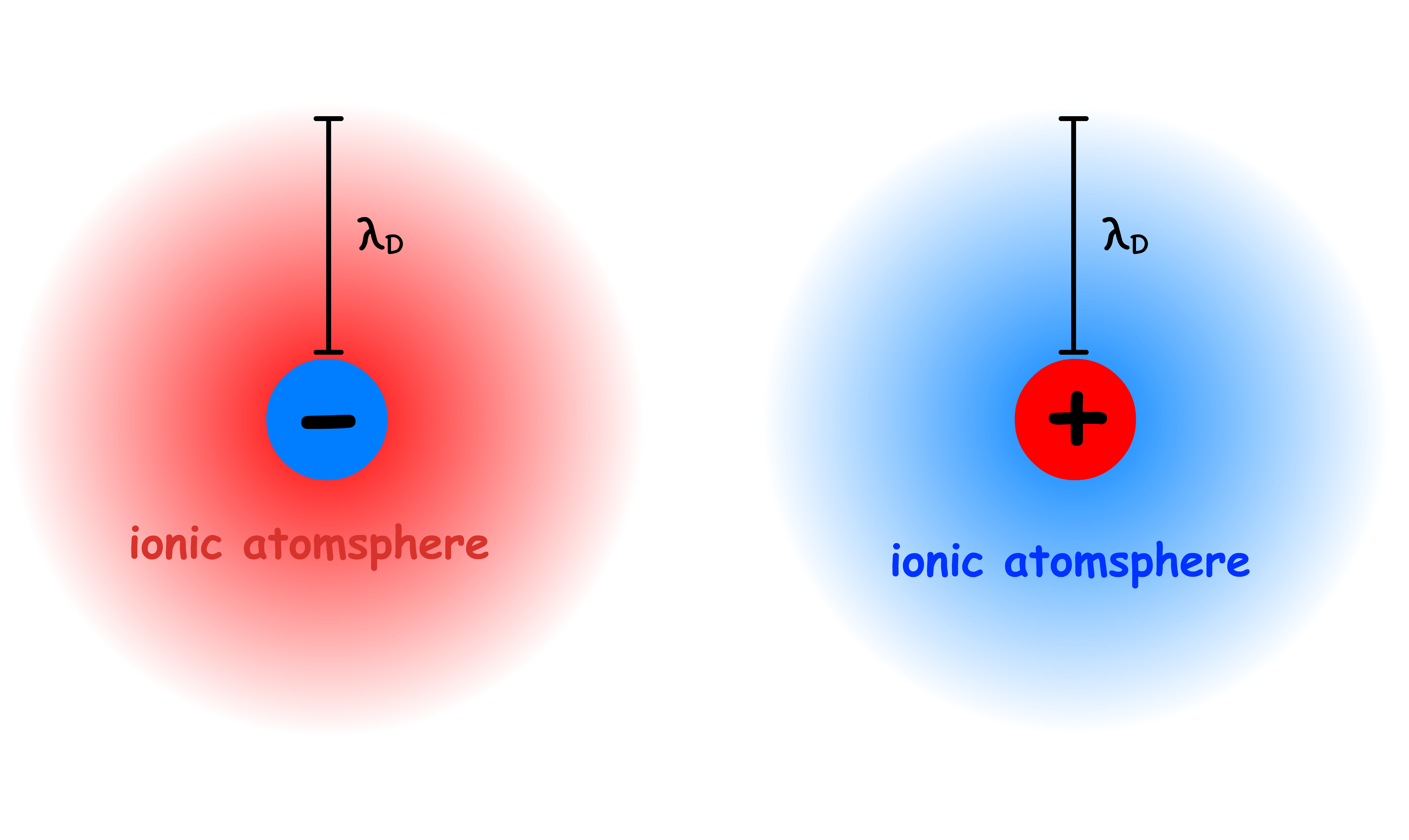
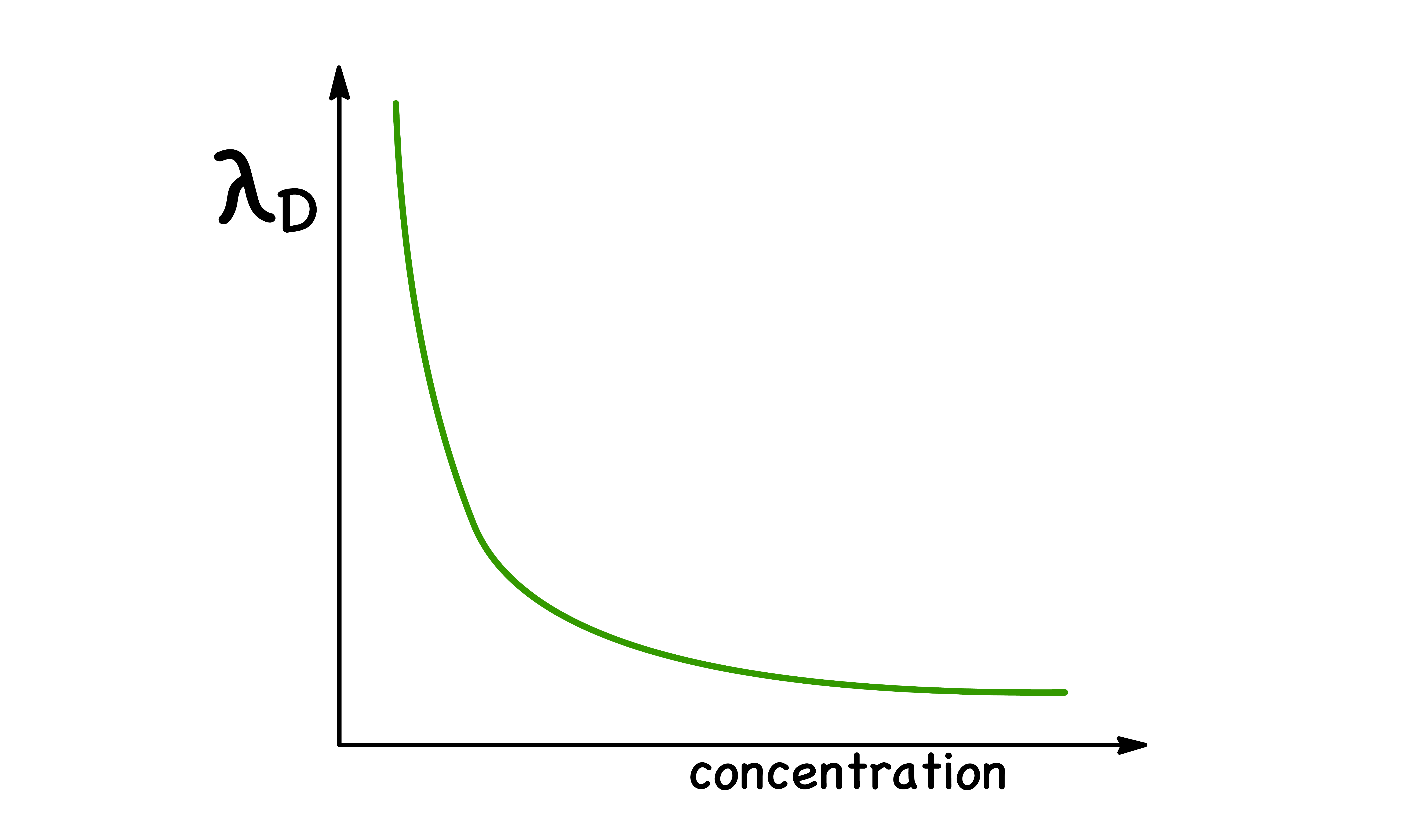
We wish to quantitatively discuss the size of an ionic atmosphere by defining the effective thickness of the ionic atmosphere
- The effective atmosphere radius is the Debye Length,
- If the ionic atmosphere were replaced by a point charge of the same magnitude situated at a distance of from the central ion, the effect due to it at the central ion would be exactly the same as that produced by the ionic sphere
- An increase in concentration of the solution results in a smaller ionic atmosphere, as fewer ions are needed in proximity to the central ion to form the atmosphere.
- In other words, the ionic atmosphere becomes larger and more diffuse as the concentration decreases
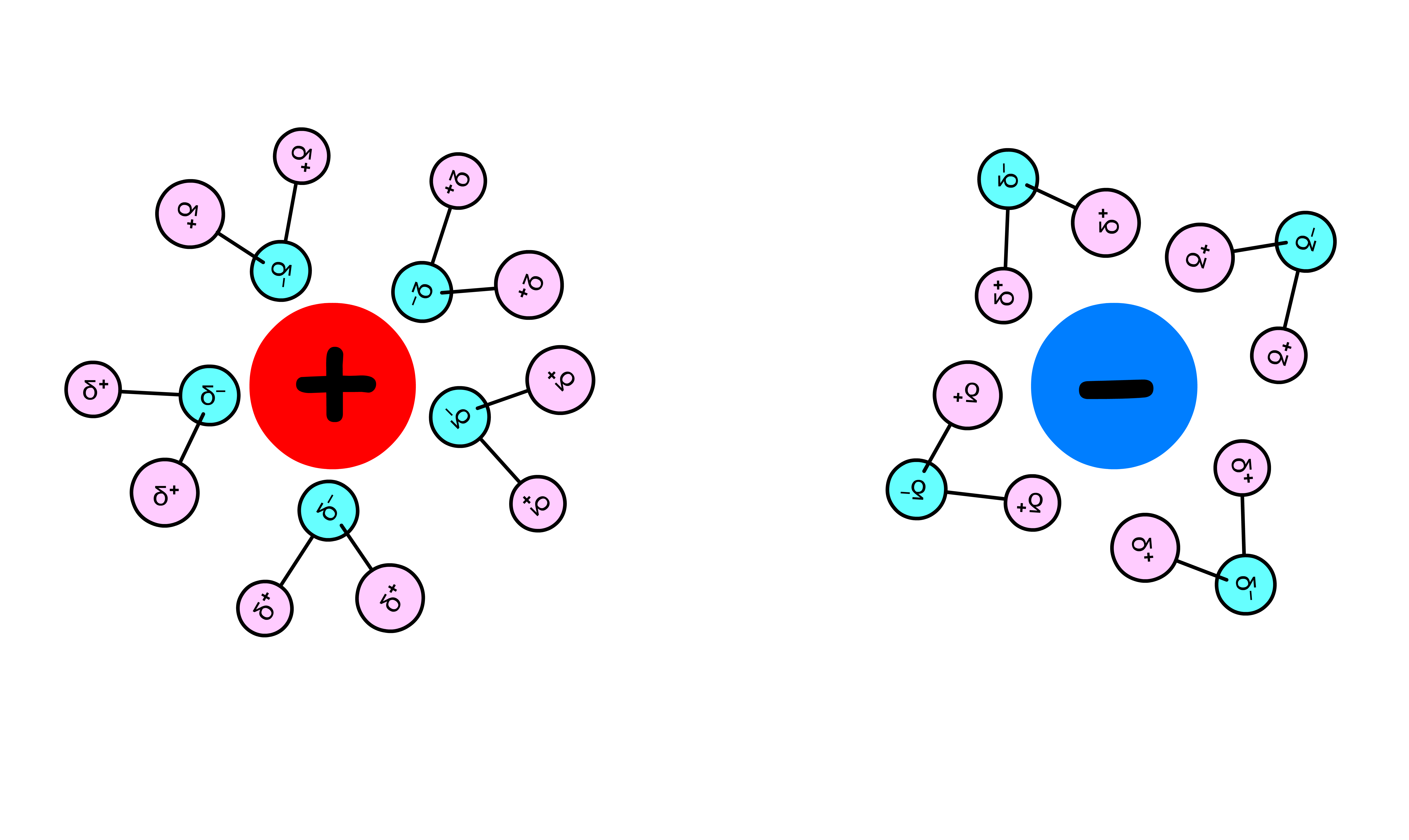
¶ Ion Pairing
Ion pairing is the process of two oppositely charged ions coming together to form a complex or association in solution
- This happens when oppositely charged ions approach each other and their attractive force overcome their tendency to remain separate due to thermal motion. As a result, the ions may form an ion pair, albeit a transient one
The phenomenon of ion pairing depends on four things
- The concentration
- The solvent
- Charge Density
- Temperature
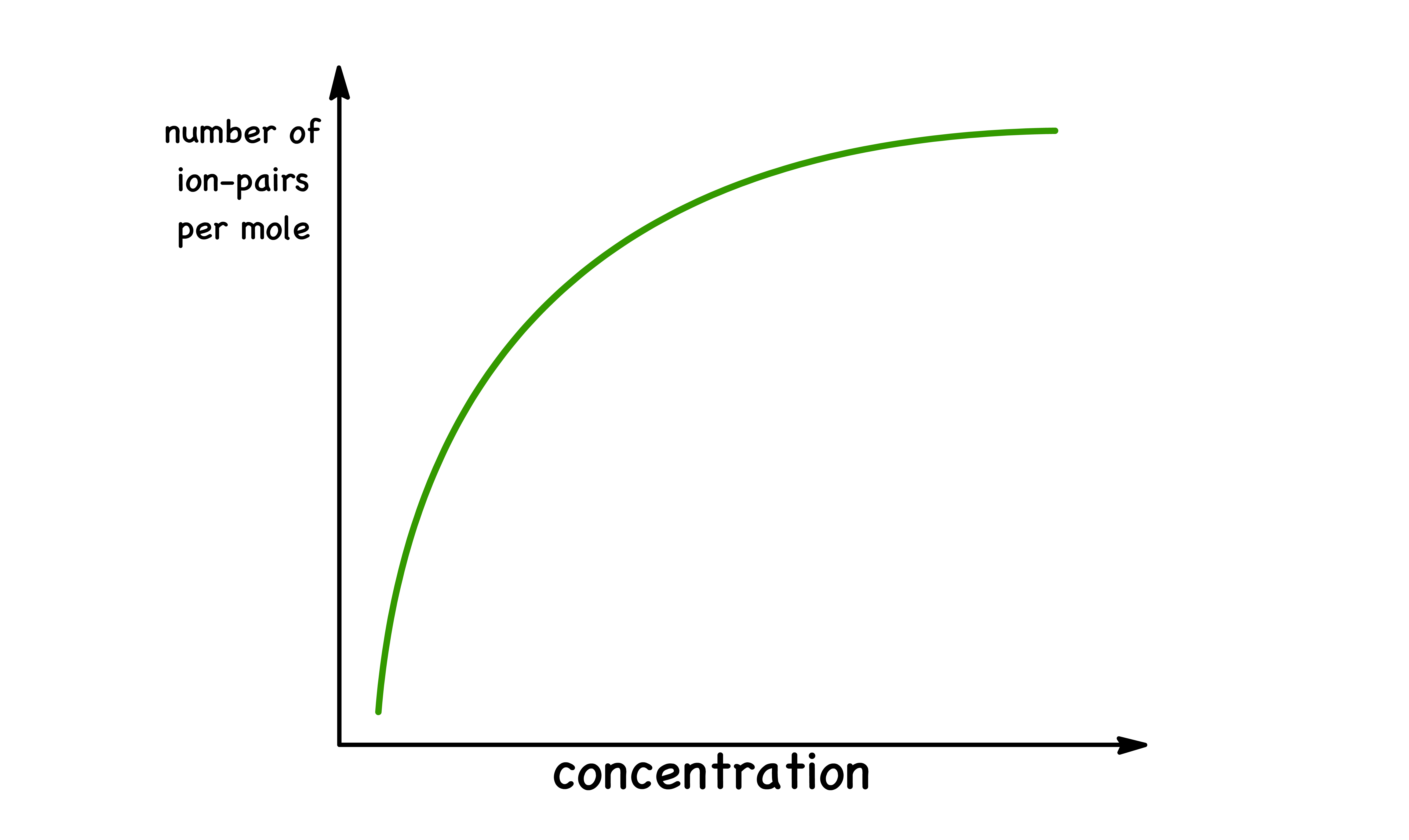
Concentration
In general, ion pairing can become more prominent at higher concentrations
- Higher concentrations of ions typically lead to a greater likelihood of ions being in close proximity, as there are more ions present in a given volume of solution
- The increased proximity of ions can increase the likelihood of attractive interactions between oppositely charged ions, leading to ion pair formation
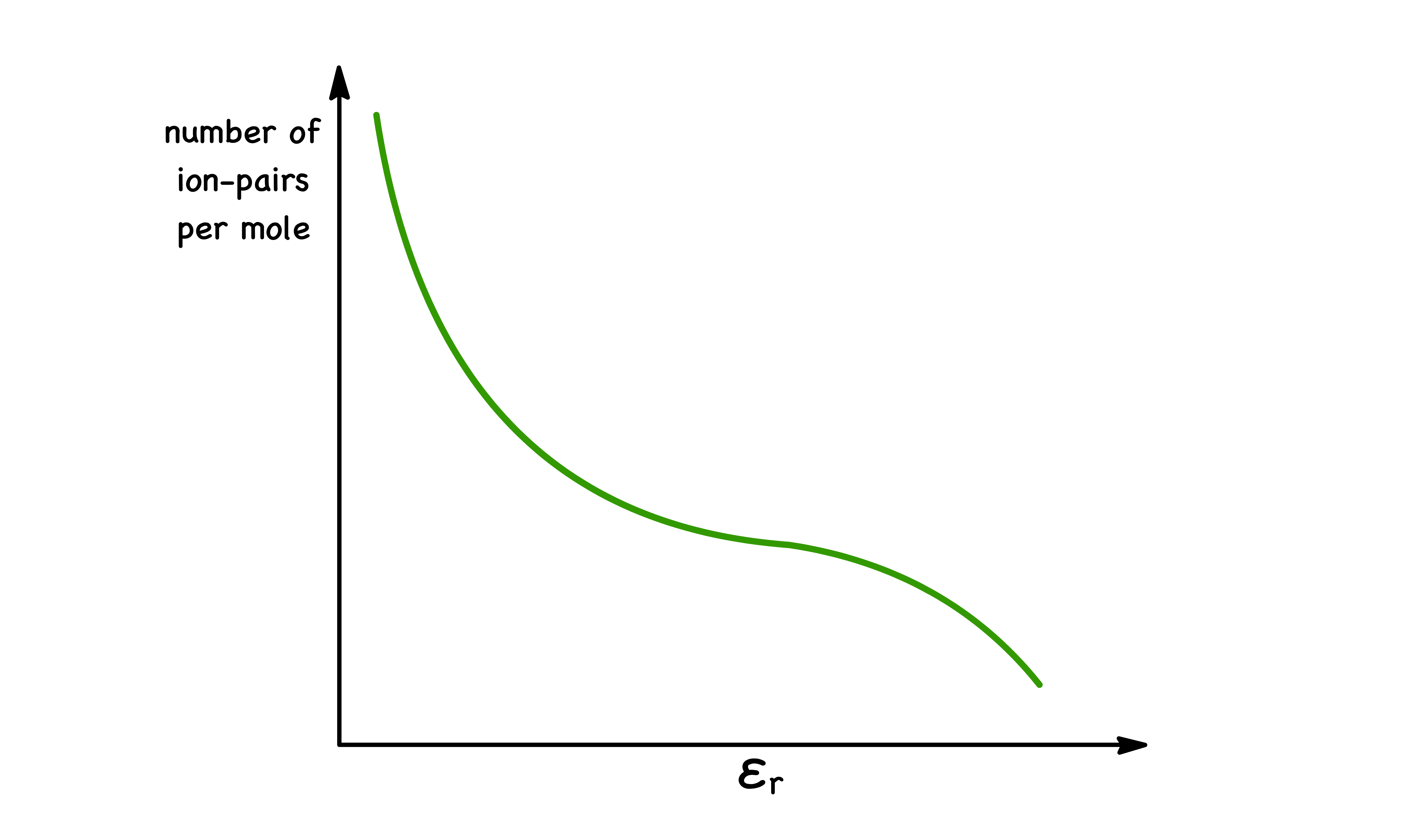
Solvent
In general, the ion pairing will happen to a greater degree when the solvents has a low dielectric constant,
- Quantitatively, this is because the attraction force between ions is inversely proportional to
- Solvents that have high dielectric constants ( Polar solvents ) tend to be more effective at stabilizing ions in solution, thereby reducing the attraction between ions
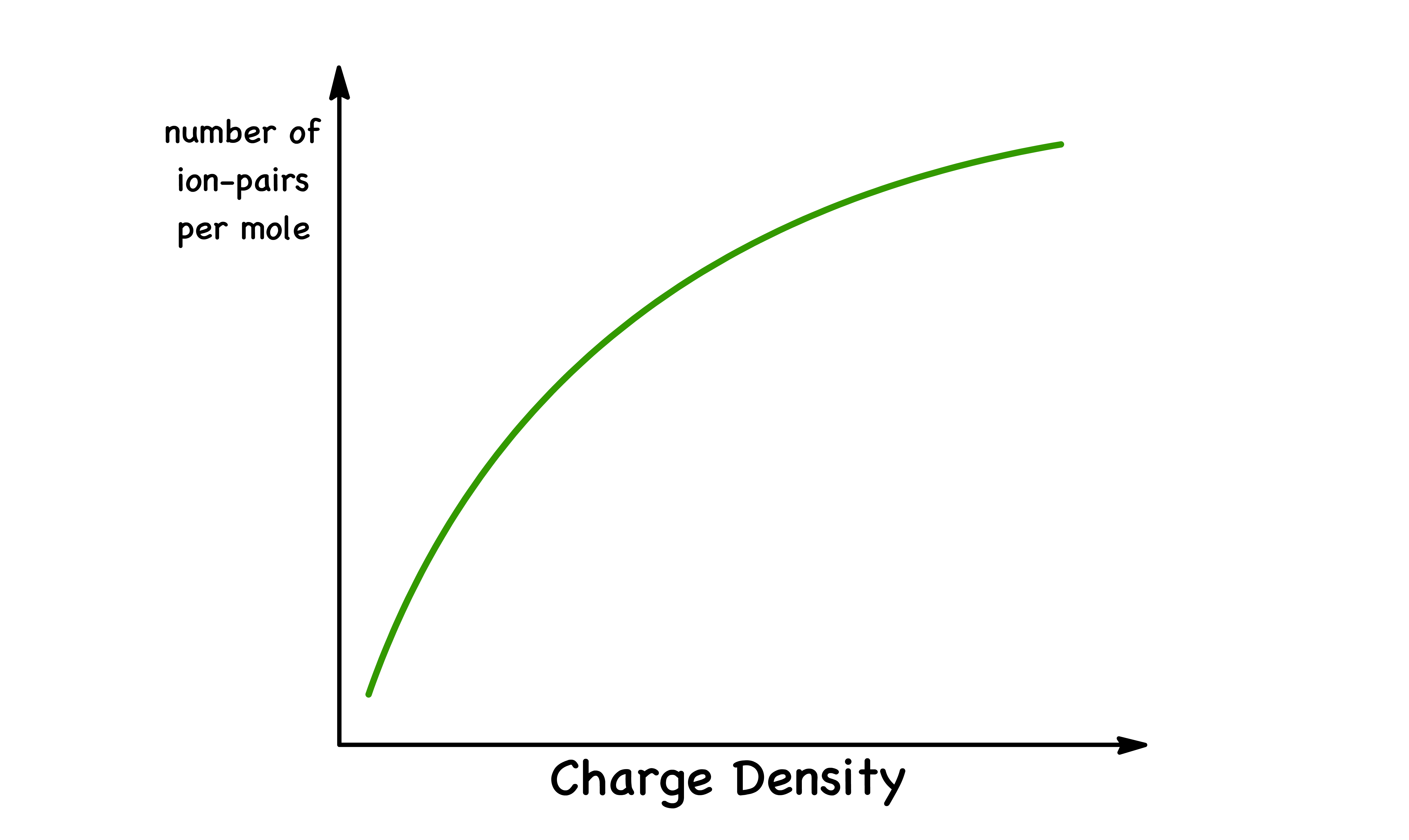
Charge Density
In general, ions with high charge densities ( i.e. high charge per unit area ) are more likely to form ion pairs
- This is because ions with high charge densities tend to have stronger electrostatic attraction
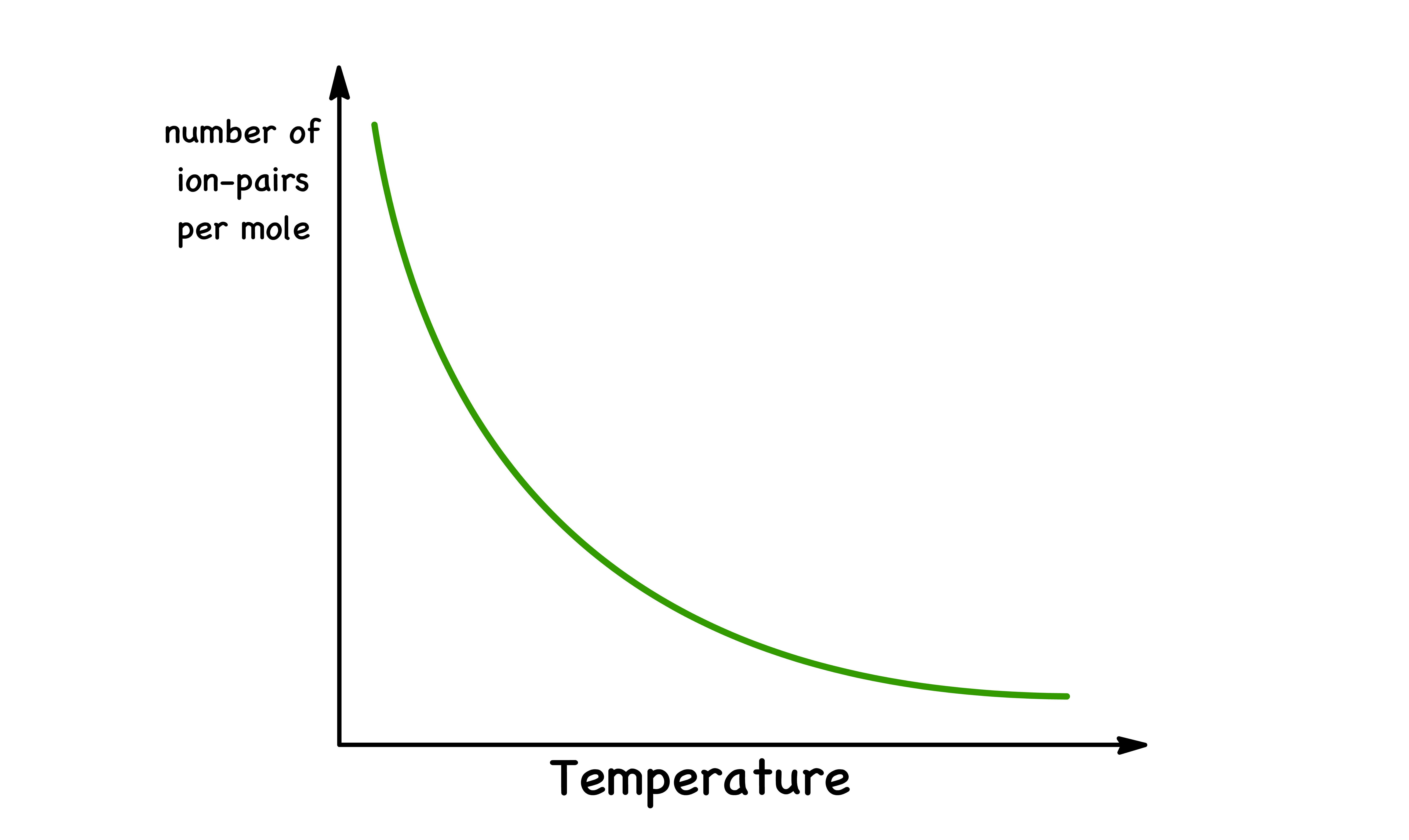
Temperature
In general, increasing the temperature can reduce the tendency for ions to form ion pairs
- Increasing the temperature will increase the thermal motion the ions and reduce the time they spend in close proximity to each other
- This effect is more pronounced for ions with weaker attractive interactions, which are more easily disrupted by thermal motion
¶ Ion-solvent interactions
Ion-solvent interactions are the electrostatic interactions that occur between ions and solvent molecules in solution
The strength of ion-solvent interactions depends on the nature of the ions and solvent
- Solvents with a high dielectric constants are polar, and so they have a strong columbic interaction with the ions
¶ Hydration Shells
- An extremely common that is used to dissolve electrolyte is water, so we shall explore its interaction with ion
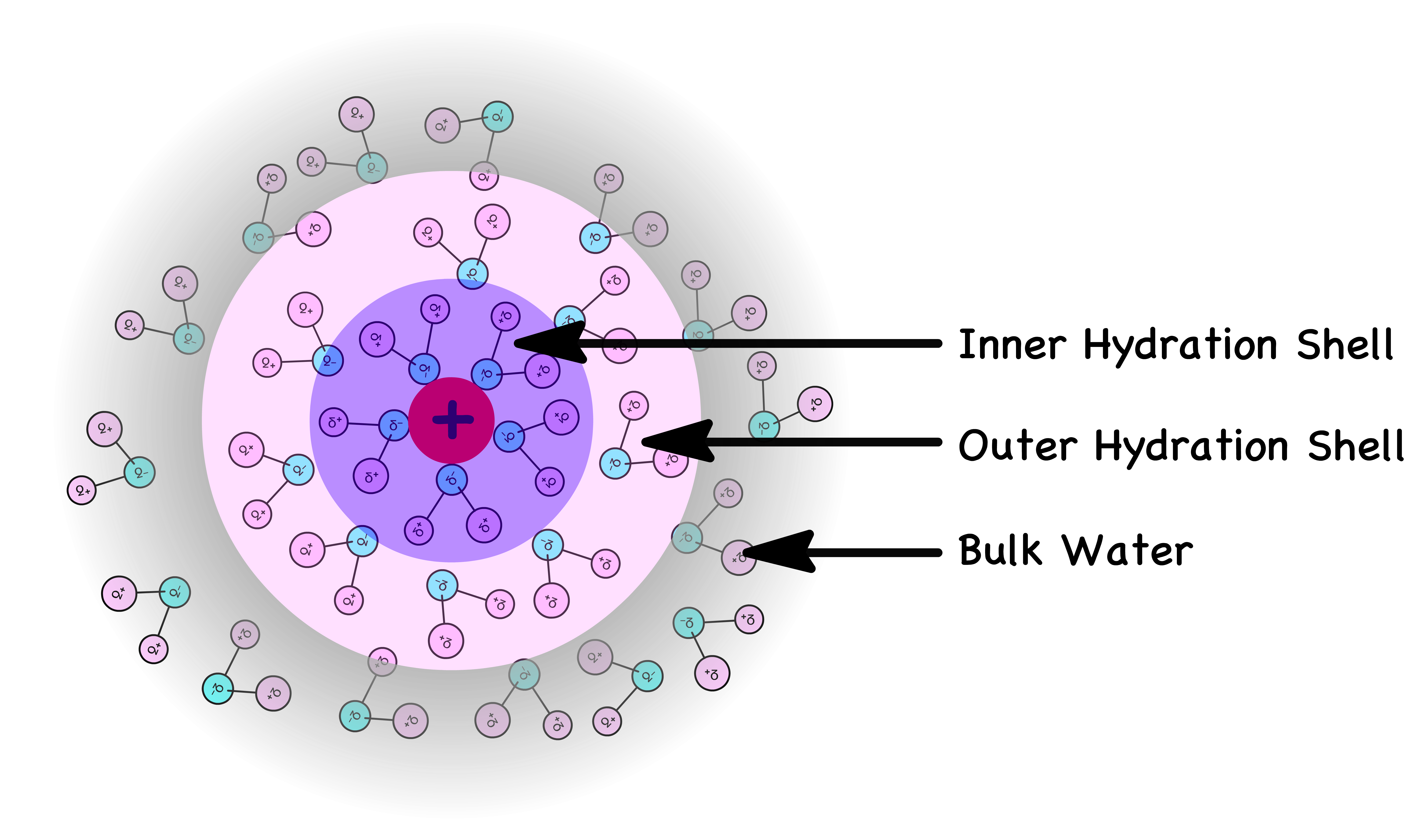
We can place the water molecules surrounding an ion into three categories
Primary (inner) hydration shell
- Water molecules within this shell is held tightly to the ion and moves with the ion
- These water molecules are in effect ligands, not solvents
Secondary (outer) hydration shell
- Water molecules within this shell has disrupted structure but does not move with the ion
The dielectric constant of water can vary depending on its local environment, including whether it is in the primary or secondary hydration shell around an ion
- In general, water molecules in the primary hydration shell may experience a slightly different dielectric constant than those in the bulk solvent or in the secondary hydration shell
- This is because the local electric field around the ion can influence the orientation and polarization of the nearby water molecules, which can in turn affect the dielectric constant
¶ Activities
This section focuses on adjusting equations from previous chapters so as to account for deviations from ideal behavior
- The expressions used to deal with ideal solutions can be kept mostly the same with the introduction of the "Activity"
- Activity can be thought of as a kind of effective mole fraction
The effective mole fraction may, in a real solution, differ greatly from the actual mole fraction as a result of the interactions between the molecules
- The extent to which this is so is measured by the activity coefficient,
- When the solution is ideal, the activity should equal that of the actual mole fraction ( )
- In other words, the activity coefficient is 1 when the solution is ideal
In terms of Molality instead of Mole fraction
It is possible to express activity in terms of molality instead of mole fraction
- We divide by such that it will become a unitless quantity ( just like mole fraction ) while having the same numerical value as
- The expressed in terms of molality will have a different value from the expressed in terms of mole fraction
- Activity can therefore also be thought of as a kind of effective molality / concentration
Having constructed this new parameter, we shall use it to quantify how much the chemical potential of a real solution deviates from ideality
- The expression of the chemical potential of a real solution can be obtained by replacing the mole fraction with activity
- Activity can be expressed in term of mole fraction ( ). Using some logarithmic properties, we can rearrange the expression as such
- The sum of the first two terms on the RHS of the equation is nothing but the chemical potential of the ideal solution
- All the deviations from ideality are contained within the last term
¶ The Activities of Ions
We want to understand the relationship between Gibbs energy of an ideal electrolytic solution and a real electrolytic solution
- Suppose we have some electrolyte that dissociates into ions in an electrically neutral solution
- The total molar Gibbs energy of the ions in an ideal electrolytic solution and a real electrolytic solution is given by
- Substituting in the expression that relates the chemical potential of real and ideal solution to the equation will give us
- The first term is nothing but the Gibbs energy of an ideal solution. We can then use some logarithmic properties to obtain the expression
- The last term accounts for deviation from ideality
Mean Activity Coefficient
- There is no experimental way of separating the into individual contributions from the cations and the anions
- The best we can do experimentally is to assign responsibility for the deviation equally to both kinds of ion
- We do so by creating a new parameter, , such that the new expression now looks like this
- Simply by comparing the two expressions, we can relate the mean activity coefficient with the activity coefficient of the cations and the anions
¶ The Debye-Hückel Theory
Although defining helps us to understand the extent of deviation from ideality in an electrolytic solution, it would be more advantageous to be able to calculate without relying on experimental measurements
- To do so, we shall resort to the Debye-Huckel Theory, which is a highly simplified model of an electrolyte solution to derive theoratical expressions for the ionic activity coefficient \gamma_
Debye-Huckel Theory is a highly simplified model and makes numerous assumptions about the electrolytic solutions
- All the deviation from ideally dilute behaviour is due to Columbic interactions between the ions
- The ions in the solution are spherical and have a small size relative to the distances between them
- The electrolytic solution must be very dilute such that the only phenomenon we have to take into account of is ionic atmosphere. In other words, the effect of ion pairing and ion-solvent interaction is ignored
- Ion-solvent interactions are neglected, meaning that the solvent is treated as a homogeneous medium with a uniform dielectric constant,
- The theory only applies to strong electrolytes and not weak electrolytes since it assumes that all ions are completely dissociated, which is not the case for weak electrolytes.
¶ The Origin of The Debye-Hückel Limiting Law
The derivation for the Debye-Hückel Limiting Law is long-winded but fruitful
- The following are the steps we should undertake to obtain an expression for
¶ Step 1: Relation between work and γ
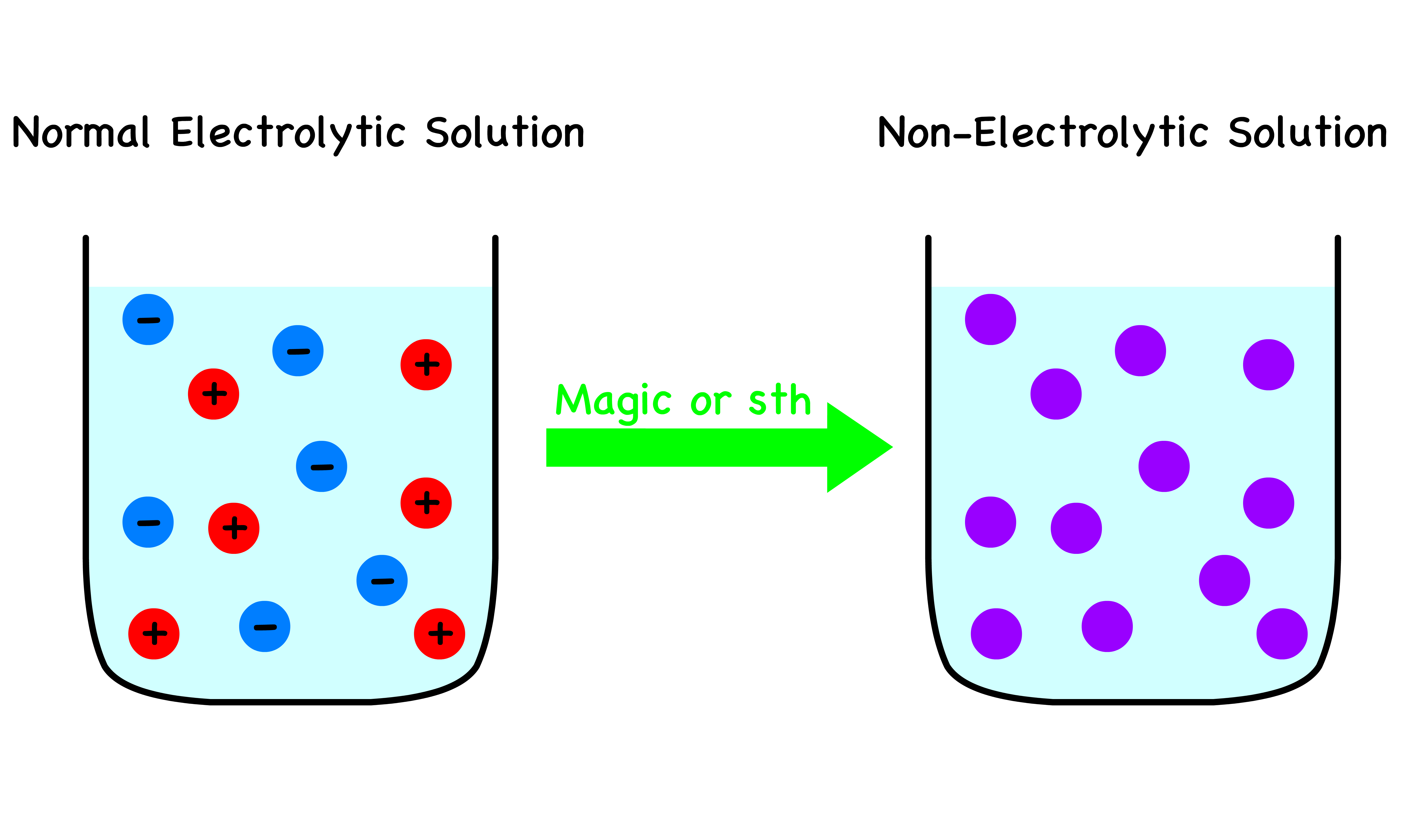
Suppose that the ions in an electrolytic solution have been magically deprived of their charge
- Since there is no ion in the non-electrolytic solution, there is no Columbic interaction
- In other words, the non-electrolytic solution is an ideal solution
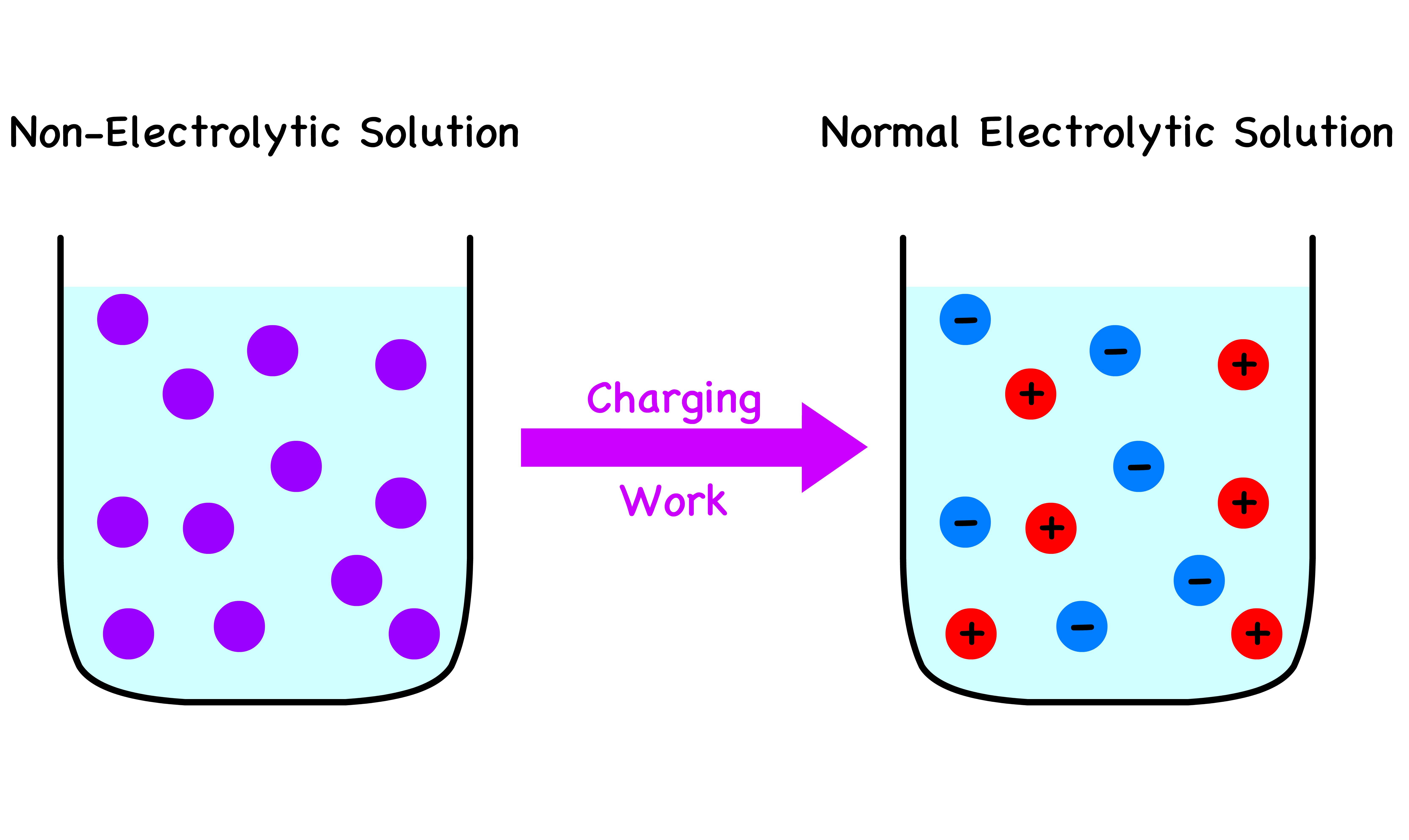
We would now like to somehow charge the non-electrolytic solution back to the original electrolytic solution
- To do so, we must put in some electric work
Electric Work and Gibbs Energy
We are interested in determining the magnitude of this electric work
- Recall from Year 1 notes that all the non-expansion work is given by the difference in molar Gibbs Free Energy
- Here, the only non-expansion work is the electric work
- The here is given by the difference in molar Gibbs energy of the charged and uncharged solution
- The charged and uncharged solutions are nothing but the real electrolytic solution and the ideal solution respectively
- We have previously derived an expression of the real molar Gibbs energy in terms of the ideal molar Gibbs energy for electrolytic solutions, . Substituting that in and doing some rearrangements will give us
- We are able to express in terms of electric work. If we can find an expression for electric work, we can easily calculate
¶ Step 2 : Expression for Electric Work
The infinitesimal amount of electric work, , is defined as the infinitesimal change in amount of charge , , moving throught some electric potential ,
- The change in amount of charge is easily measurable, so all we need to do is to determine what the electric potential is
The Potential Due to Charge Distribution
- Under normal circumstances, the electric potential at a distance away from an isolated ion of charge is given by
- The presence of the ionic atmosphere causes the potential caused by the point charge to decay faster than usual
- To calculate the work of charging the central ion, we need to know the potential at the ion due to the ionic atmosphere , which is given by
- The potential experienced by the central ion is nothing but the potential exerted by the ionic atmosphere at
Having determined the electric potential experienced by the central ion, we can rewrite the expression for the infinitesimal amount of electric work
- We can then integrate both sides to get the expression for charging up one ion
- The charge of an ion must be a multiple of the charge of an electron, so we can say
- Finally, we are interested in the molar electric work needed for charging up the solution, so we simply have to multiply the expression by
¶ Step 3: Simplification and Final Expression
Recall that we have are able to relate the activity coefficient with the total electric work
- The total electric work is just the sum of molar electric work for charging up each type of ion multiplied by the corresponding stoichiometric coefficient
- Substituting in the expression for molar electric work we just derived
- The overall solution is electrically neutral, such that
- The Debye Length can be expressed in terms of other constants and something called the ionic strength
- By convention, we wish to use rather than . The conversion can be made by dividing the expression by
- For simplicity's sake, we will call that giant behemoth of a lump of constant, A
- Since the product of and must always be negative, we can also express it as such
¶ Using the Limiting Law
While it is great that we have derived an expression that allows us to predict the value of , we must also learn how to use it
- is a proportionality constant known as the limiting equivalent conductance. The value of depends on the solvent chosen
- and are the charges of the cation and anion, respectively, in an electrolyte solution
- is the ionic strength of the electrolyte solution
¶ Ionic Strength
The ionic strength of the electrolyte solution can be expressed as such
- The factor of in front of the summation is included to avoid double-counting of ion pairs, since each ion contributes to the ionic strength equally
- We divide by such that it will become a unitless quantity while having the same numerical value as
Example
The summation in the expression is often a source of confusion, so here are two examples that allow us to understand its usageA solution of 0.1 mol kg–1 MgCl2
A solution of 0.15 mol kg–1 K2SO4 and 0.02 mol kg–1 NaBr
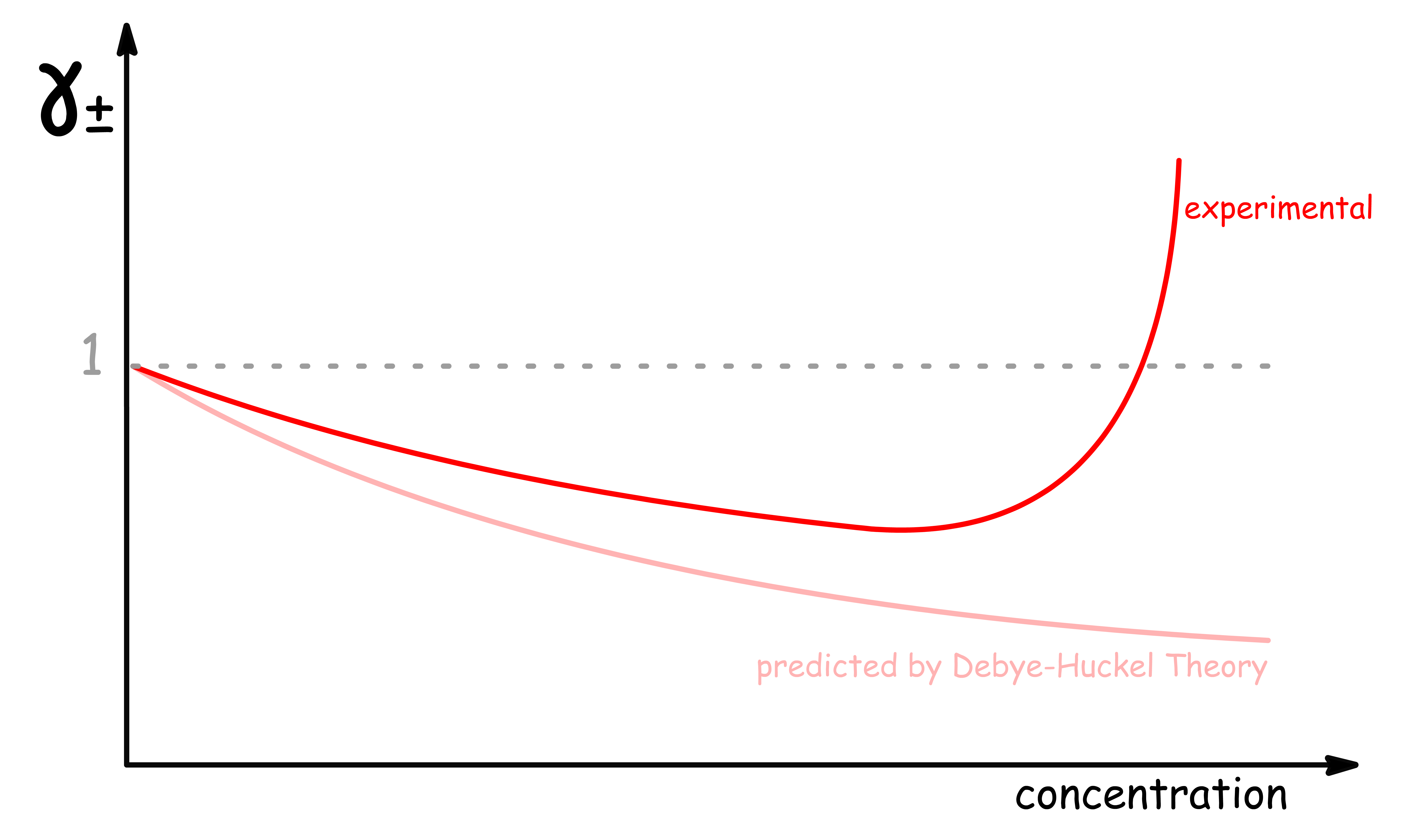
¶ The theory predicts that γ± should always be smaller than 1
The Debye-Huckle limiting law predicts that must be negative
- This means that must be smaller than 1
Effective Concentration is Lower than the Actual Concentration
Recall the relationship between activity
- Since the activity coefficient ( ) predicted by the theory must be smaller than 1, the activity must be smaller than the actual concentration
- In other words, the Debye-Huckel Theory predicts that the effective concentration is always smaller than the actual concentration
Lowering of Free Energy
Recall that the real Gibbs energy can be expressed as such
- The Debye-Huckel Theory predicts that must be smaller than 1, so the last term must be negative. As a result, the real Gibbs energy must be smaller than that of the ideal Gibbs energy
- The lowering of free energy predicted by the Debye-Huckel Theory is based on the phenomenon of ionic atmosphere and the resultant stabilization it brings along
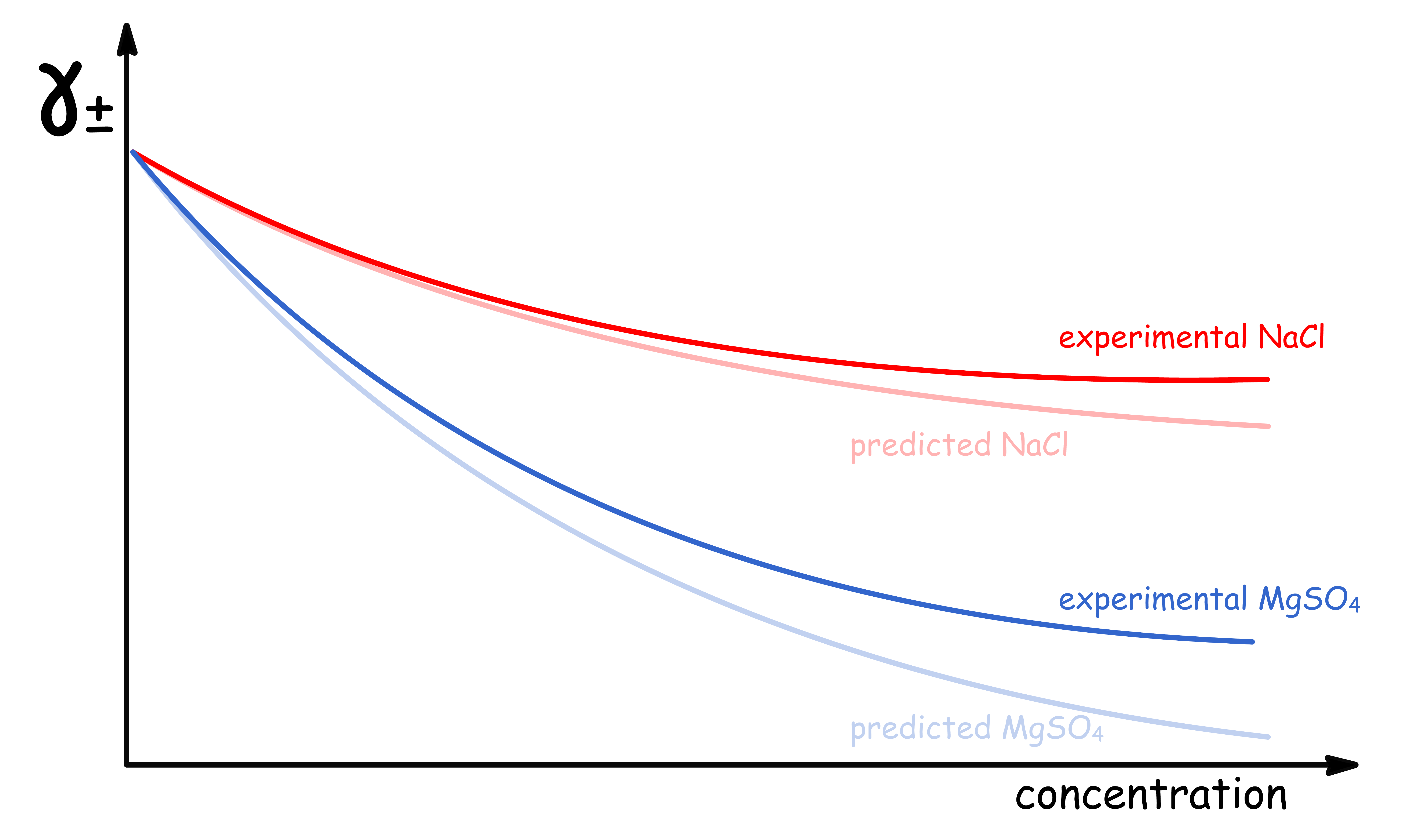
¶ The Failure of The Limiting Law
While the Debye-Hückel limiting law is generally applicable to dilute solutions, it fails to accurately predict the behavior of electrolytes at higher concentrations
- This is because the theory only takes into account of ionic atmospheres, but not ion-pairing and ion-solvent interactions
- At higher concentrations, the effects of these interactions and the finite size of ions become more significant, leading to deviations from the predictions of the Debye-Hückel limiting law
¶ Theory and Experiment Only Agrees when the Ionic Strength is Low
- The behavior of electrolyte solutions is complex, and the relationship between theory and experiment can be challenging to reconcile
- The theoretical models used to describe electrolyte behavior makes grossly simplifying assumptions that are only valid when the interaction between ions is minimal
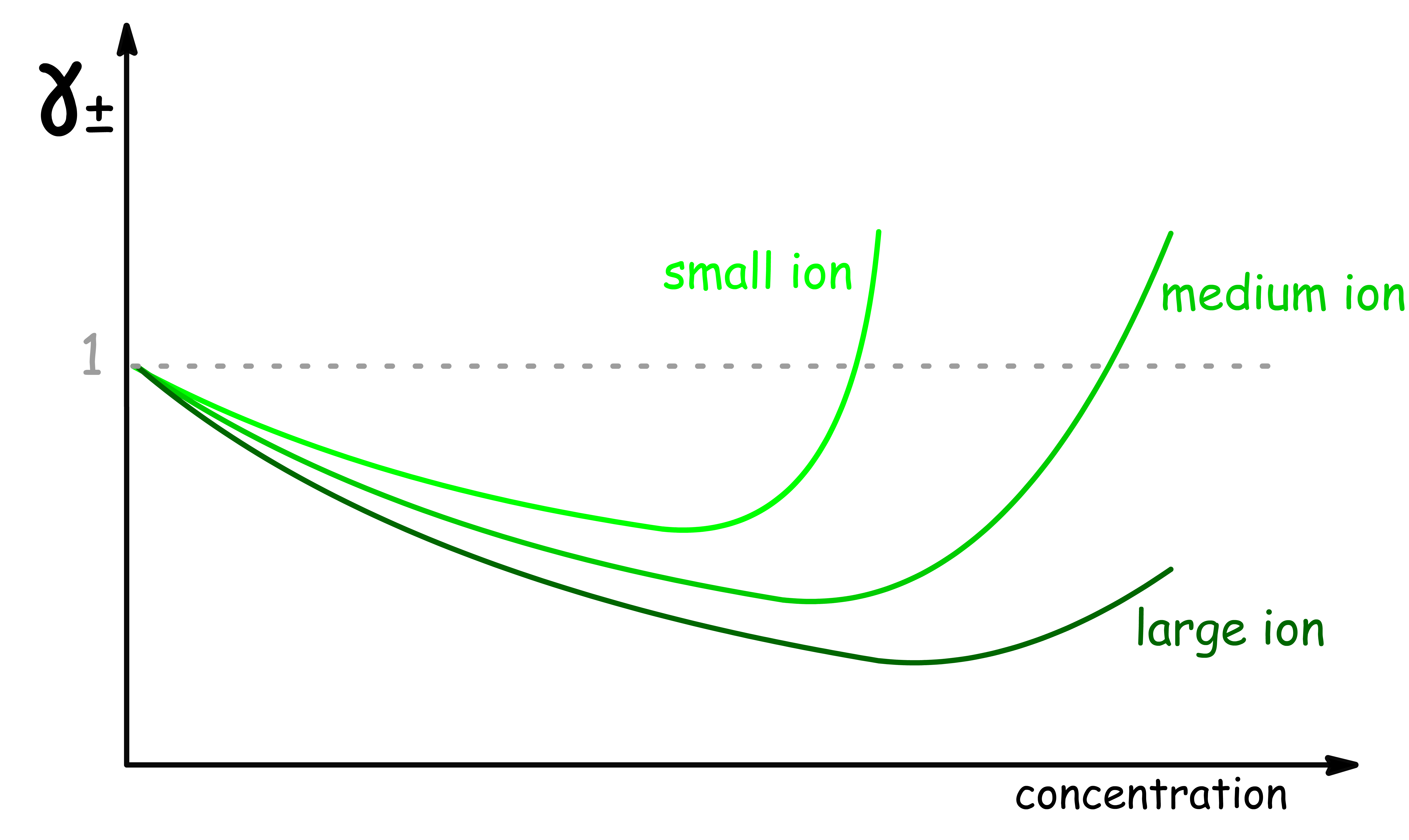
¶ Real γ± can exceed value of 1
Using the prediction made by the Debye-Huckel theory, we should expect that the value of to always be lower than 1
- However, experimental results indicates that can have values greater than 1 at higher concentrations
- In other words, the effective concentration can sometimes be greater than that of the actual concentration
This happens because of ion-solvent interactions
- Solvents behave like ligands in the primary hydration shell, so they are not free solvent molecules
- At high concentrations, the effect of ion-solvent interaction become more prominent and the number of free solvent molecules decreases
- As the ions tie up solvent molecules, the effective concentration ( i.e. the moles of solute per kg of free solvent ) becomes greater than that of the calculated concentration ( i.e. the moles of solute per kg of all solvent )
This effect also depends on the size of the ions
- For ions of the same charge, the deviation from the Debye-Huckel theory is actually greater for smaller ions
- This is because smaller ions have a higher charge density and therefore have a stronger interaction with the solvent molecules in their primary hydration shell
- This results in a larger reduction in the number of free solvent molecules and a higher effective concentration compared to larger ions
¶ Conductivity
¶ Conductance ( G )
Conductance (G) is a measure of the ability of a material to conduct electrical current
Conductance and Flow of Charge
- Current is defined as the rate of flow of charge through a cross-sectional area of a conductor, while voltage is defined as the difference in electric potential
- The conductance is therefore directly proportional to the rate of flow of charge
- In other words, the conductance is large when the charge carrying particles are moving quickly or when the charge they are carrying is large. For electrolytic solutions in particular, we can say
Conductance, Area and Length
The prcess of conducting electricity can be thought of as workers carrying charges through a tunnel
- If the cross-sectional area of the tunnel is big, more workers can be travelling through it at the same time. As a result, more charges is carried through the tunnel per unit time
- If the length of the tunnel is long, it will take longer for the workers to make it out of the tunnel. As a result, less charges is carried through the tunnel per unit time
- In general, the conductance of an object increases with cross-sectional area and decreases with length
- is the proportionality constant
¶ Conductivity ( κ )
- Conductance ( ) is not a good measure of a material's ability to conduct electricity as it depends on its size
- We can improve the comparison if we choose a measurement that is independent of the size of the conductor and depends only on the property of the conductor itself
Conductivity ( κ ) is the conductance of a unit cube
is more than just a proportionality constant. We can extract a richer meaning of if we consider the conductance of a material with the size of a unit cube
- When the conductor is a unit cube, its cross-section area and length must be 1
- Hence, the conductance of this unit cube is just the conductivity of the material ()
¶ Molar Conductivity ( Λm )
- Conductivity ( ) is not a convenient quantity for the study of conduction by electrolytic solutions as it depends on the concentration of the solution
- We wish to devise a quantity that ( at least in principle ) depends on the identity of the electrolyte and solvent only
The molar conductitvity ( ) is defined as the conductivity divided by concentration of the electrolyte
- The importance of the molar conductivity is that it gives information about the conductivity of the ions produced in solution by 1 mole of substance
¶ Molar Conductivity's Dependence on Concentration
Since the molar conductivity, denoted by , is defined in a manner that eliminates the effect of concentration on conductivity, we may expect it to be unaffected by the concentration of the electrolyte
- In other words, if we were to double the concentration of charge carriers, we would anticipate the molar conductivity to also double, but since the concentration of the electrolyte would also double, would remain unchanged
- The basis of this assumption is that doubling the concentration of the electrolyte would actually double the concentration of the charge carriers
- However, this assumption is not valid. Experiments reveal that the concentration of charge carriers increases at a slower rate than the concentration of the electrolyte
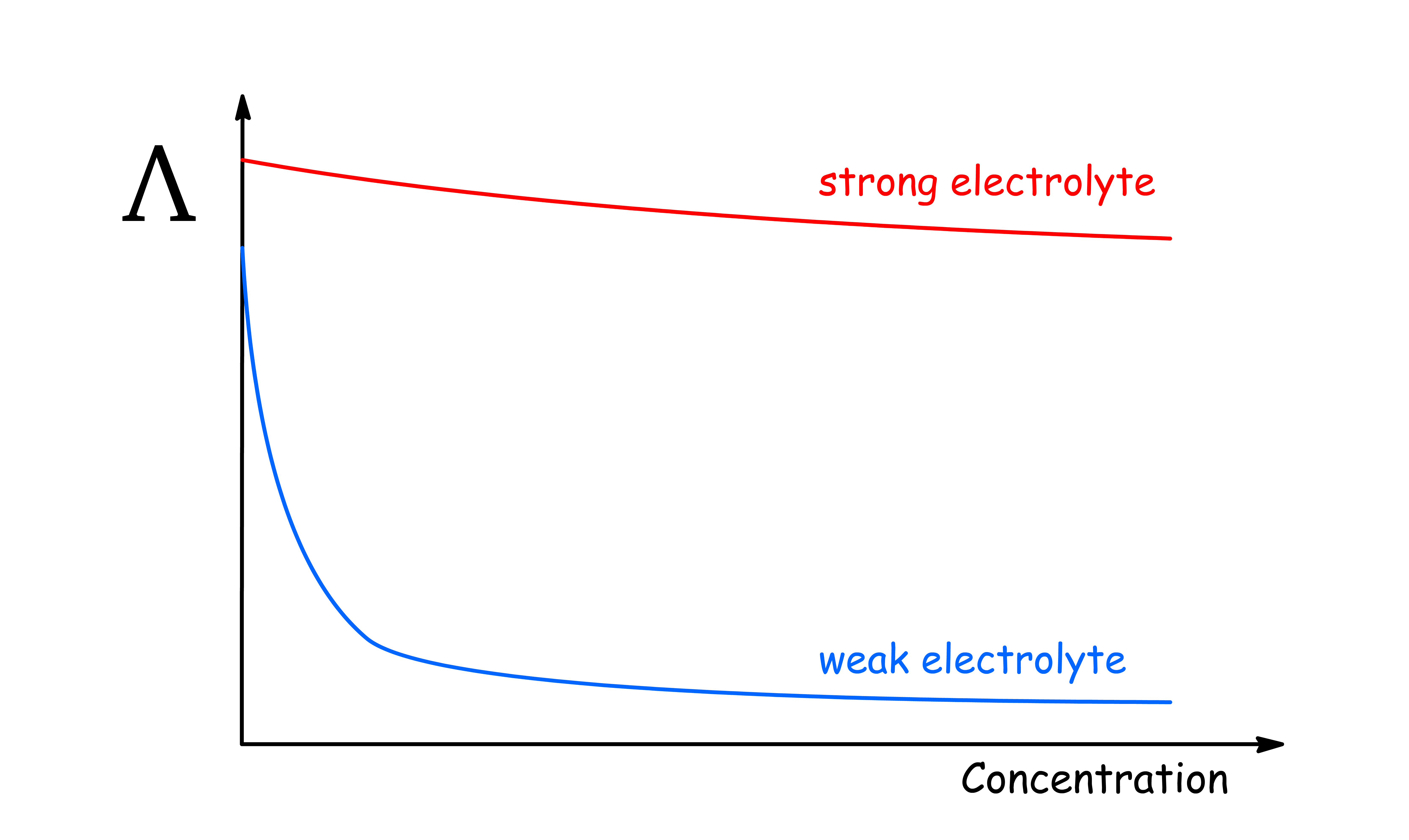
Despite the fact that molar conductivity is intended to provide a means of comparing the conductivity of different electrolyte-solvent combinations without taking concentration into account, it is important to note that molar conductivity actually varies with concentration
- In general, the molar conductivity will decrease as the concentration increases
- The trend may seem counterintuitive at first since conductivity usually increases with concentration. However, note that we are talking about molar conductivity, not regular conductivity
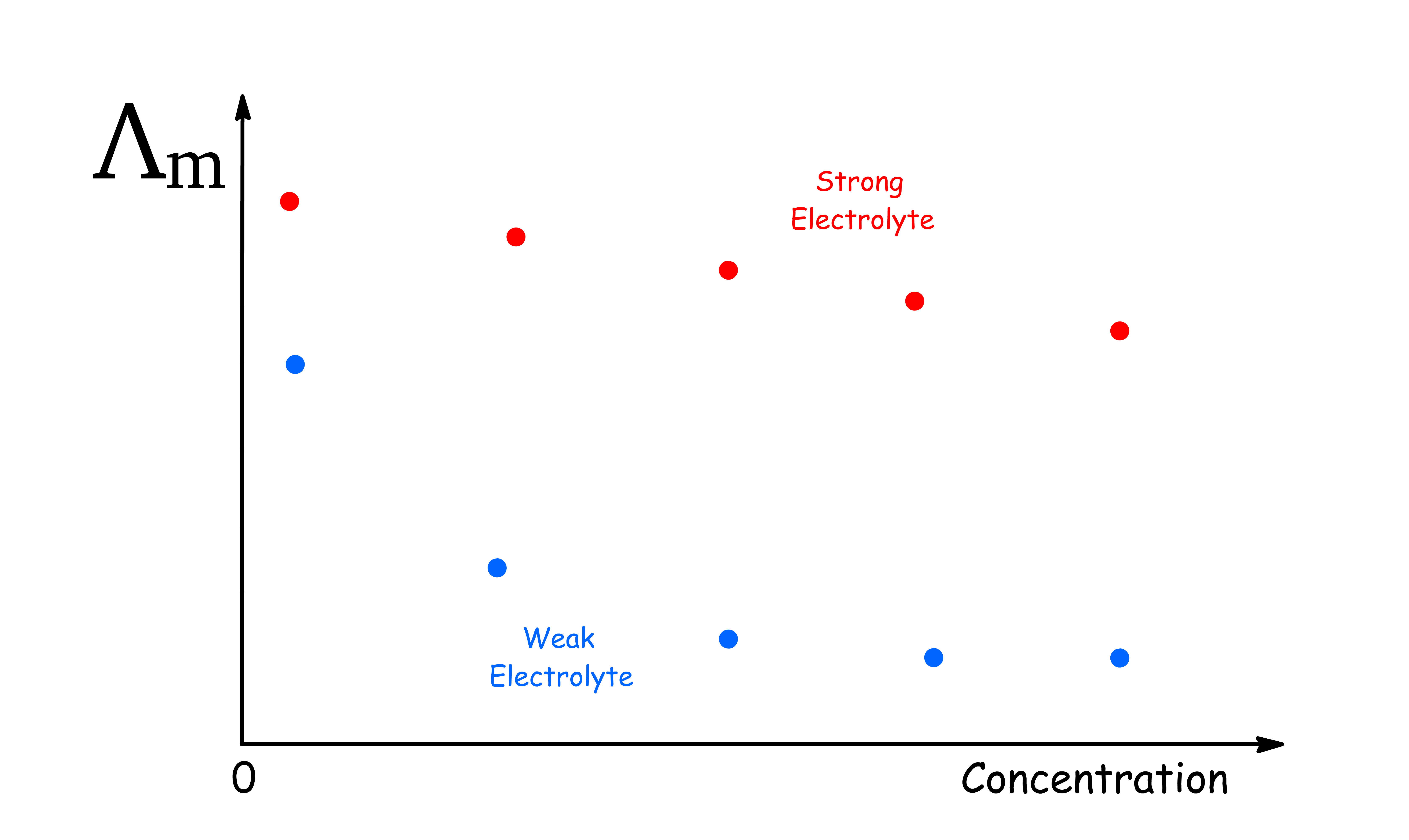
The trend is different for Strong and Weak electrolytes
In all cases, the molar conductivity diminishes as the concentration is raised, and two patterns of behaviour can be distinguished
- For strong elecytrolytes, the molar conductivity only falls slightly when the concentration is raised
- For weak electrolytes, the fall in molar conductivity is much more pronounced
It turns out the reason behind the decrease in molar conductivity is different for strong and weak electrolytes
¶ Why the Molar Conductivity of Strong Electrolyte decreases when the concentration is raised
There are three reasons why the molar conductivity of Strong Electrolyte decreases when the concentration is raised
- Relaxation and Asymmetry ( related to ionic atmosphere )
- Electrophoretic Effect ( related to ionic atmosphere )
- Ion-Association ( related to ion-pairing )
Relaxation and Asymmetry
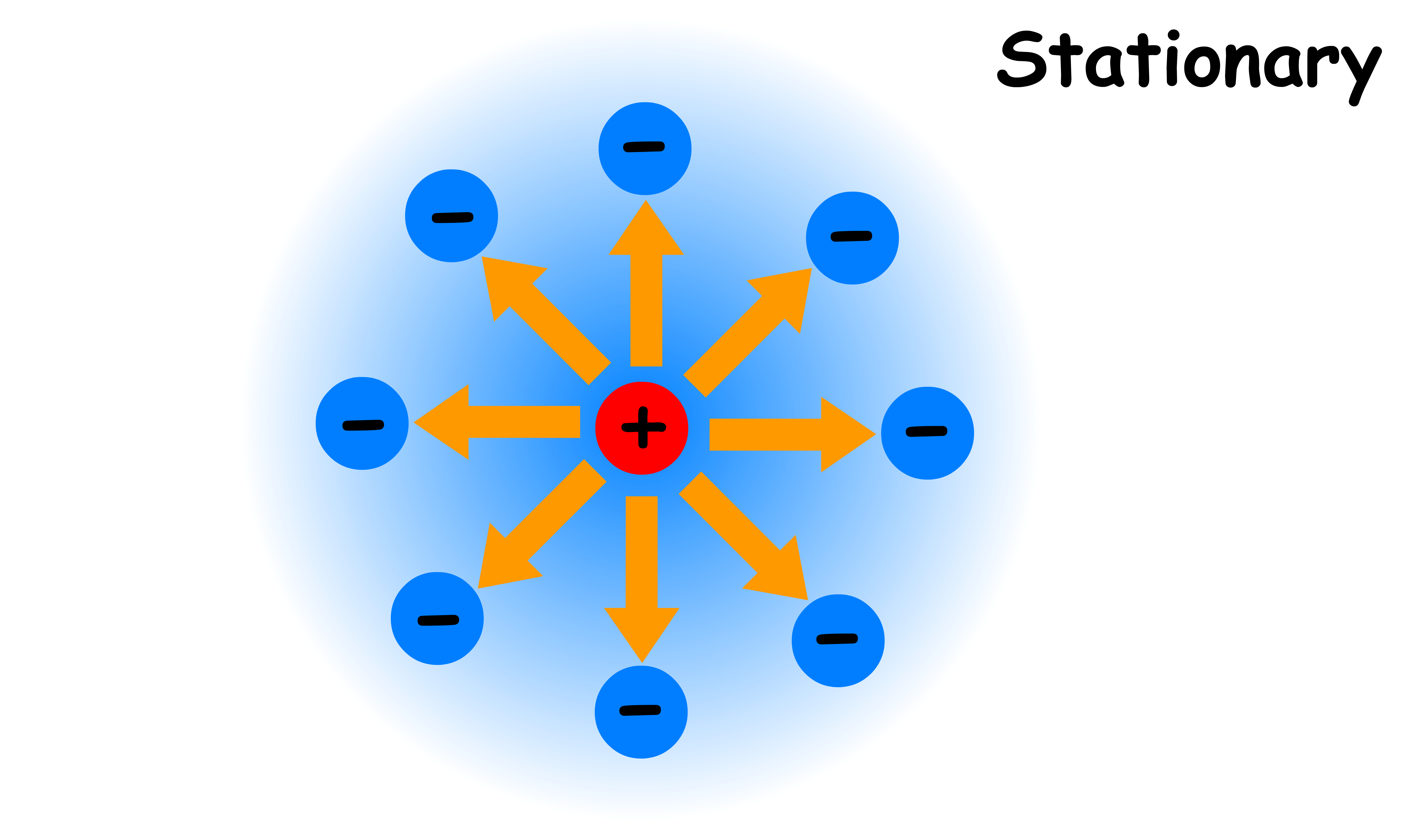
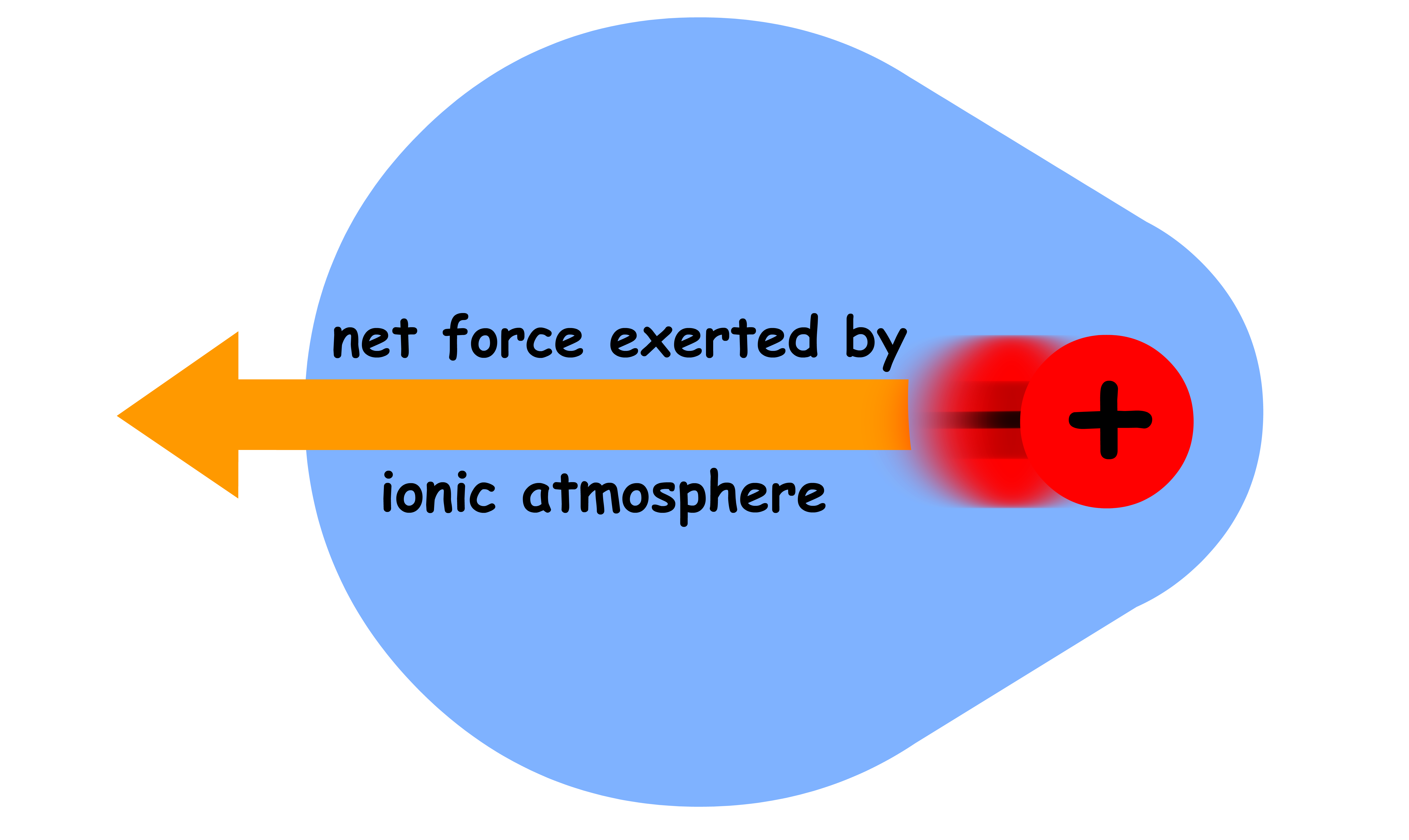
When the central ion is stationary, the ionic atmosphere will be arranged symmetrically about it
- Due to the spherical symmetry, the ionic atmosphere is pulling on the central ion equally in all direction
- As a result, there is no net force exerted on the central ion by the ionic atmosphere when the central ion is not moving
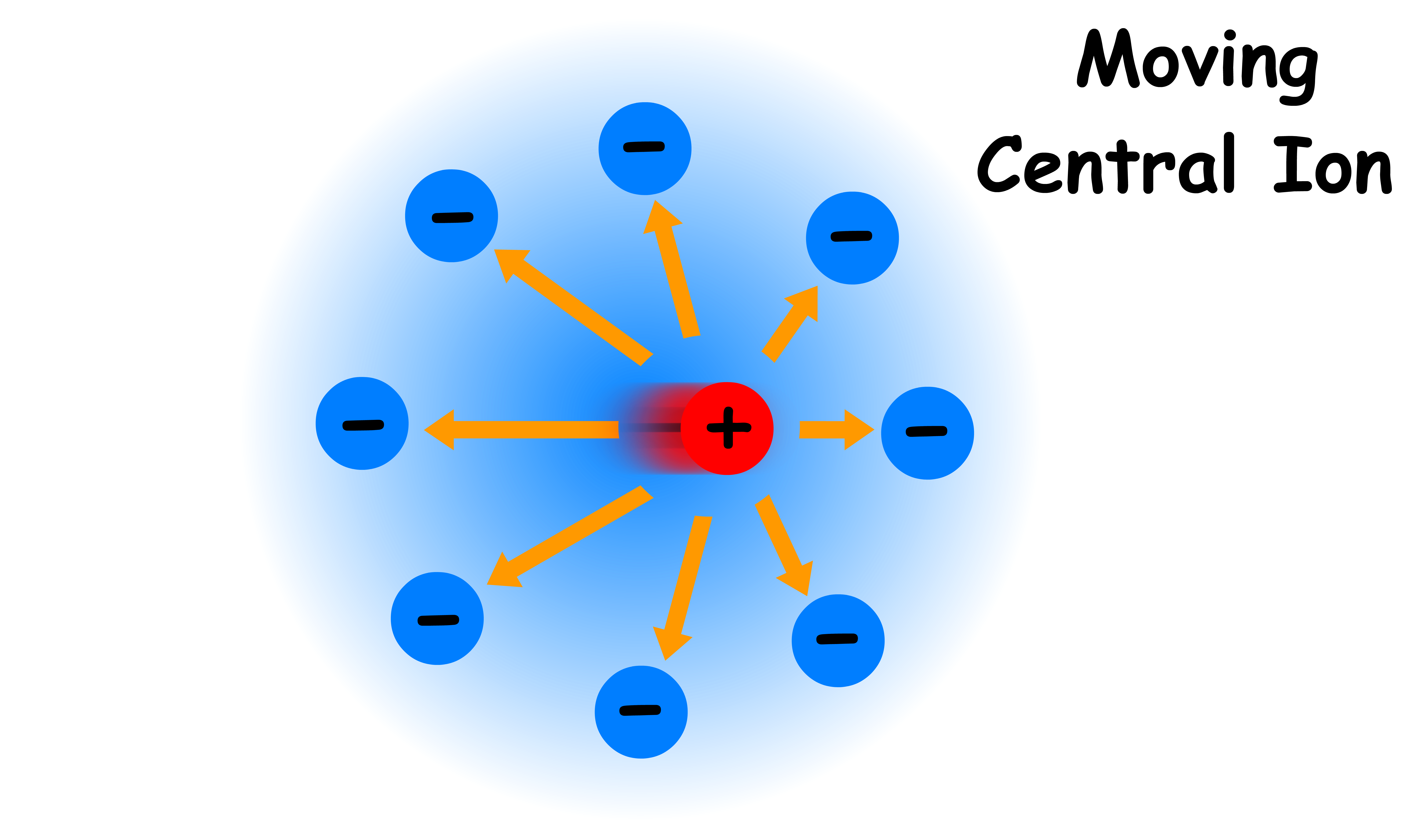
However, when the central ion starts moving, the ionic atmosphere will decay to some extent and the spherical symmetry will be lifted
- The charge density behind the central ion is greater than that in front, which means the central ion experiences a net force by the ionic atmosphere in the opposite direction of motion
- The effect is similar to that of friction as it slows down the speed of the central ion
- Since conductivity directly proportional to the speed of ions and the influence of ionic atmosphere increases with concentration, conductivity decreases when the concentration is raised
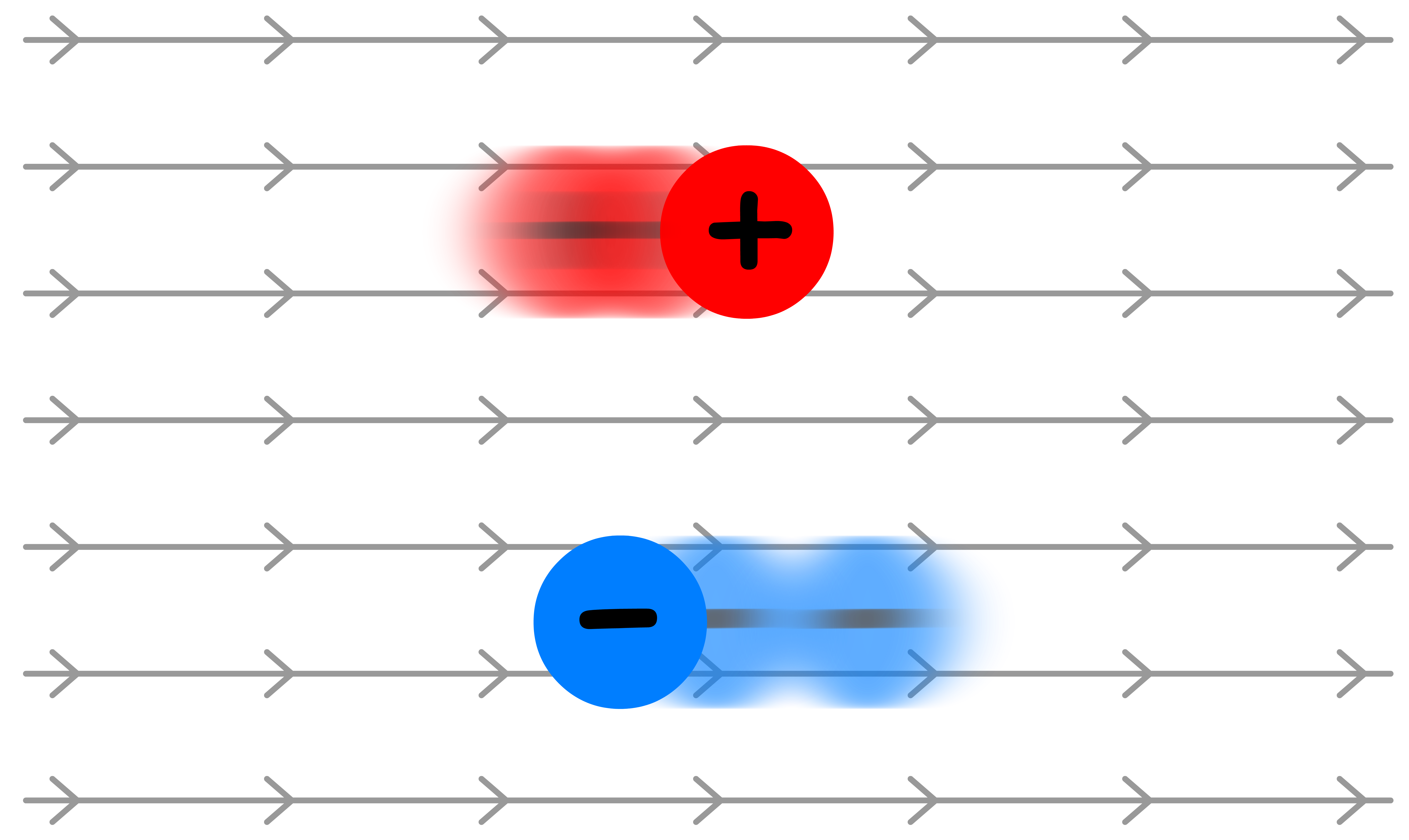
Electrophoretic Effect
The reason why ions move is because of the presence of an electric field
- Cations move along the electric field, while anions move against the electric field
Since the central ion and the ionic atmosphere are of different charges, they must move in the opposite direction under the influence of the same electric field
- The opposing motion of the ionic atmosphere will tend to drag solvent molecules due to the attractive forces between ions and solvent molecules
- As a result, the central ion is required to move upstream
- Since conductivity directly proportional to the speed of ions and the influence of ionic atmosphere increases with concentration, conductivity decreases when the concentration is raised
Ion Association
In a solution, ions have the ability pair up with each other, resulting in the formation of electrically neutral complexes or complexes with a smaller charge than the individual ions
- Since these complexes possess a lower charge than the individual ions, they will move slower in the presence of an electric field
- As a result, the electrical conductivity of the solution decreases
¶ Why the Molar Conductivity of Weak Electrolyte decreases when the concentration is raised
Solutions of weak electrolytes also experience a decrease in molar conductivity as its concentration increases
- It turns out weak electrolytic solutions also share the same issue as strong electrolytic solutions, but to a much smaller extent
- The main contributor for the plummet in molar conductivity of weak electrolytic solution is something entirely different
Degree of Dissociation
The main reason for the decrease in molar conductivity of weak electrolytic solution is different than that of strong electrolytes
- Weak electrolytes undergo a process known as dissociation, in which only a fraction of the solute molecules ionize into their constituent ions
- As the concentration of the weak electrolyte increases, the fraction of ionized solute molecules also increases, but at a decreasing rate
- This is due to the equilibrium between the undissociated solute molecules and the ions present in solution. As the concentration increases, the equilibrium shifts towards the undissociated solute molecules, leading to a decrease in the number of ions available to conduct electricity.
- This decrease in the number of ions leads to a decrease in the molar conductivity of the solution.
¶ Independent Migration of Ions
Background ( Why should we care )
To obtain an accurate measure of the intrinsic conductivity of ions, it is necessary to determine the molar conductivity in a solution where there are no ion-ion or ion-solvent interactions
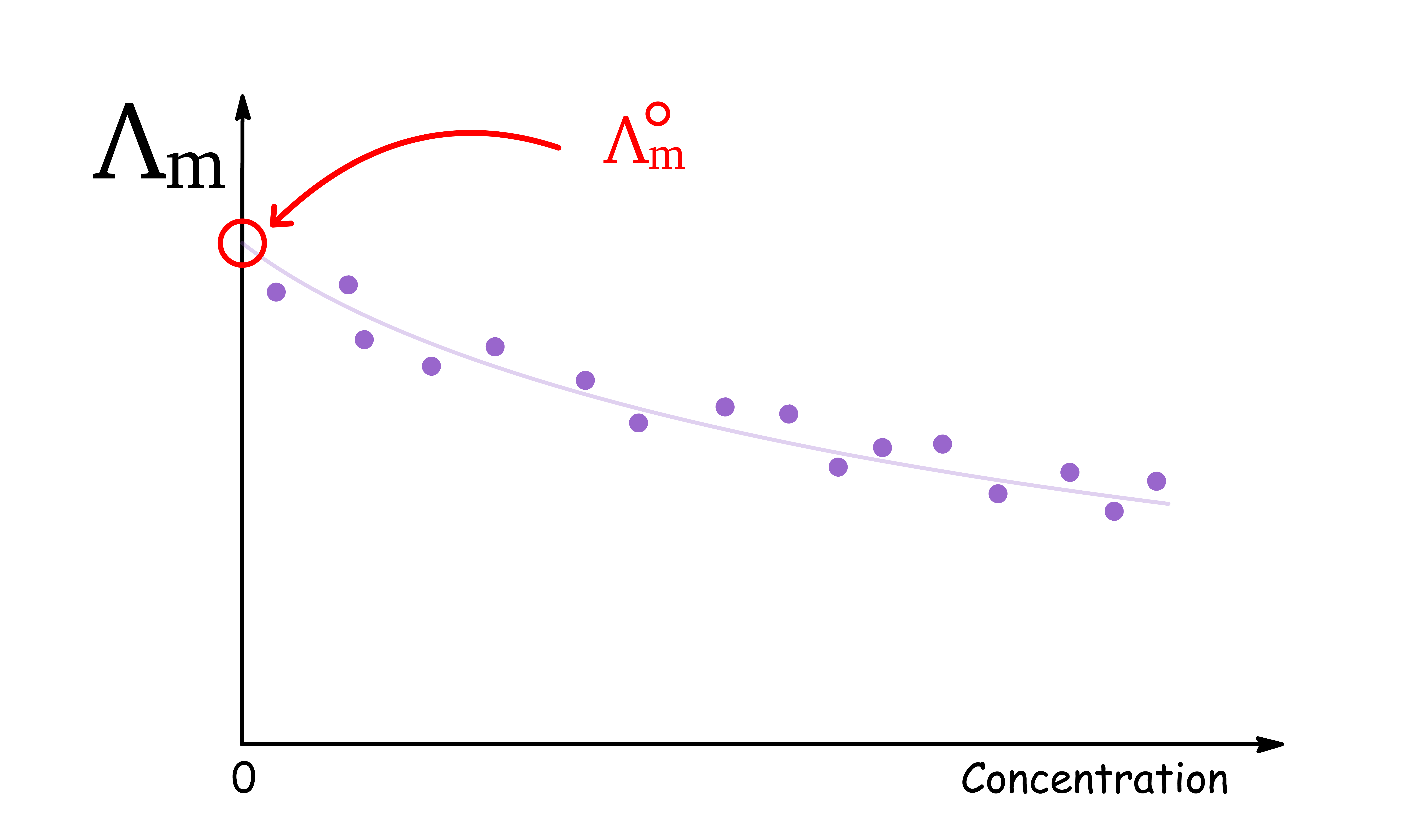
- This can only be achieved at infinite dilution, where the concentration of the electrolyte approaches zero
- However, in practice, it is impossible to measure conductivity at such low concentrations. Therefore, to obtain the molar conductivity at infinite dilution, experimental data obtained at higher concentrations must be extrapolated to the limit of
- We denote this limiting molar conductivity at infinite dilution as
Extrapolation in Strong Electrolytic Solutions vs Weak Electrolytic Solutions
In principle the plots of against concentration can be extrapolated back to zero concentration to give for any electrolytic solutions. In practice, we can only extrapolate for solutions of strong electrolytes, but not weak electrolyte
- The Debye-Huckel theory predicts that for strong electrolytes, a plot of versus is linear at low concentrations, which allows for an accurate extrapolation to infinite dilution
- However, for weak electrolytes, their molar conductivities approach their limiting value at infinite dilution asymptotically, therefore the extrapolations do not lead to reliable
To obtain the for weak electrolytes, we must rely on a different procedure
- One useful method is to exploit Kohlrausch's Law of Independent Migrations of Ions
¶ Kohlrausch's Law of Independent Migrations of Ions
Kohlrausch's Law states that the molar conductivity of an electrolyte at infinite dilution is equal to the sum of the molar conductivities of its cations and anions
- Suppose we have an electrolyte: . The limiting molar conductivity of this electrolytic solution can be expressed as such
- The meaning of the law is that each ion is assumed to make its own contribution to the molar conductivity, irrespective of the nature of the other ion with which it is associated at infinite dilution
- The condition of infinite dilution is necessary because ions start to interact with each other at any other concentration
Using Kohlrausch's Law to find for Weak Electrolytes
Kohlrausch's Law of Independent Migration of Ions provides a means to compute the for weak electrolytes, such as acetic acid. Here's how:
- Start by breaking down the limiting molar conductivity of the weak electrolyte into a sum of contributions from its constituent ions:
- Next, find the limiting molar conductivity of the cation and anion individually. This can be achieved by using extrapolated data from strong electrolytes, such as
- Use algebraic manipulation to solve for the limiting molar conductivity of the cation and anion of the weak electrolyte
- Therefore, we can use extrapolated data from strong electrolytes to relate the unknown limiting molar conductivity of the weak electrolyte with the measured values of strong electrolytes
¶ Speed of Ions
Conductivity is the ability of a solution to conduct electricity, and it is related to the speed at which ions move through the solution
- When a potential difference is applied across an electrolyte solution, ions move towards the oppositely charged electrode
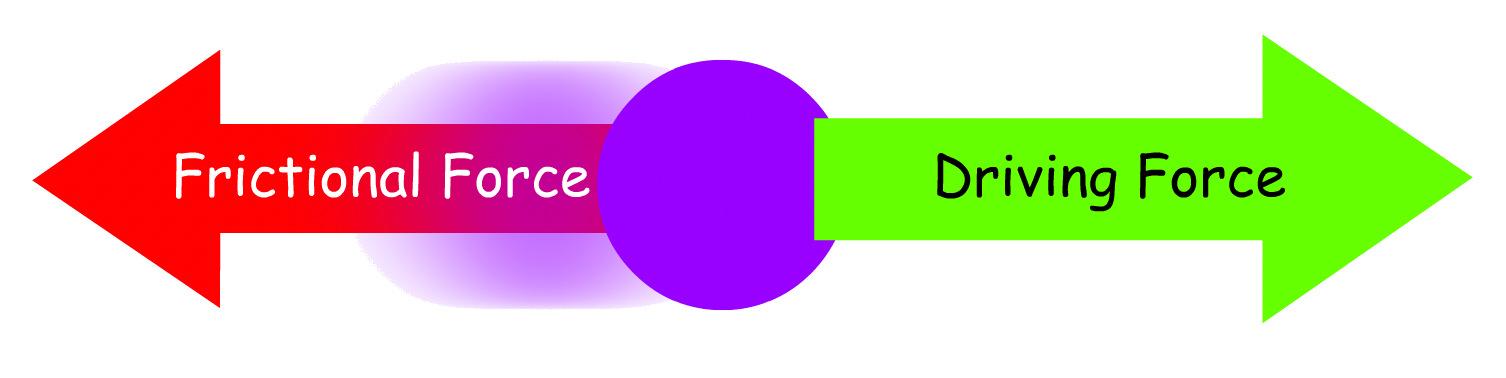
- The speed at which the ions move depends on the driving force that causes the ion to move and the frictional force exerted on the ion due to its motion
Driving Force
The driving force that moves ions in an electric field is given by
- is the driving force
- is the ion charge
- is the elementary charge ( magnitude of the charge of an electron )
- is the electric field strength, and it is defined as . and are the difference in potential and distance between the electrodes respectively
Frictional Force
The frictional force acting on an ion is proportional to the ion's speed, the viscosity of the solution, and the ion's hydrodynamic radius. The frictional force is given by:
- is the frictional force
- is the viscosity of the solution
- is the hydrodynamic radius of the ion
- is the speed of the ion
Drift Speed of an Ion
When the driving force and the frictional force are balanced, the ion reaches a steady-state drift speed
- When the two opposing force are balanced, the ion will not accelerate, but it will travel at a constant speed
- The speed at which ions move depends on the viscosity of the solution, the hydrodynamic radius of the ion, and the strength of the applied electric field
- These factors affect the frictional force acting on the ion and thus its drift speed
¶ Effect of hydration on hydrodynamic radius
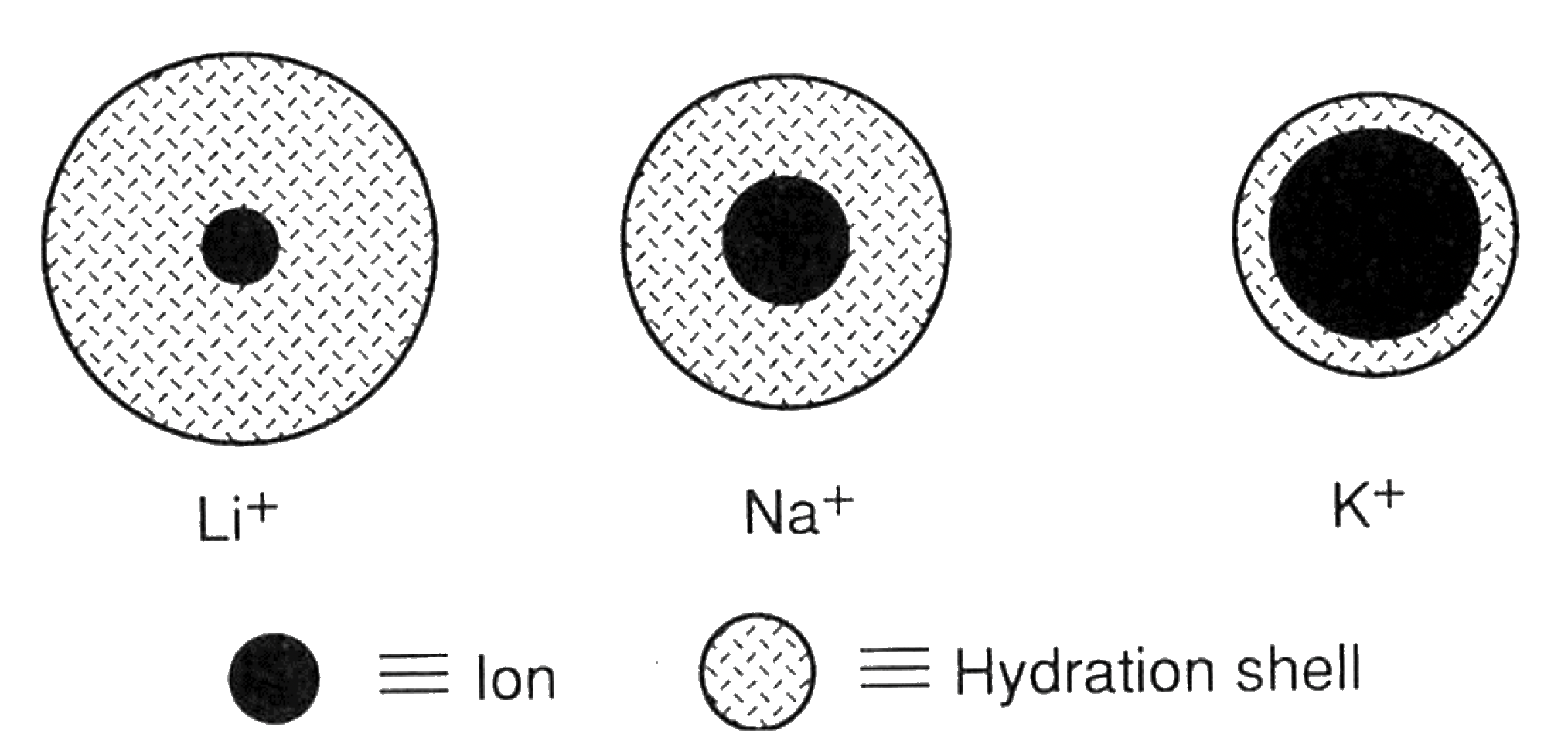
The hydrodynamic radius of the ion is the effective size of the ion as it moves through a fluid and it is inversely proportional to the drift speed
The extent of hydration is related to the electric field at the surface of the ion
- Smaller ions with the same charge will hold more water in their primary hydration shell due to their stronger electric field.
- Smaller ions tend to have greater hydrodynamic radii and thus move slower through the solution, leading to lower conductivity
- Conversely, larger ions tend to have smaller hydrodynamic radii and move more faster through the solution, leading to higher conductivity.
Anions, which are often polyatomic such as ClO4- and NO3-, are generally weakly hydrated. Even Cl-, which is a monatomic anion, is thought to have only one water molecule in its primary hydration shell
¶ Ionic Mobilities
The mobility of an ion ( ), is defined as the speed with which the ion moves when the electric field strength is 1
We can express the molar conductivity in terms of ionic mobility
- Suppose the system has the size of a unit cube, then we can express the conductivity as such
- Current is defined as the rate of change of charge with respect to time, ; Voltage is defined as the difference in potential,
- It should be obvious that the rate of change of charges across any cross-section of the conductor is just the product of the speed of ions, the magnitude of charges, the number of ions passing through an arbitrary cross-section plane of the conductor
- We can express the drift speed in terms of ionic mobility
- Recall that the electric field strength is defined as E=\frac{\Delta \phi}
- The molar conductivity is defined as the conductivity divided by the concentration
Using Kohlrausch's Law of Independent Migrations of Ions, we can express and in terms of the individual ionic mobility
- At infinite dilution, the molar conductivity can be separated into contributions from the cation and anion
¶ Transport Number
Transport numbers represent the fraction of the total current carried by one type of ion in an electrolyte solution
- Differences in transport numbers are due to different ion mobilities in solution
- The sum of all transport numbers in solution is 1
From above we know for an ion in an electrolyte solution, the current can be written as:
The transport number in terms of mobility is
- If there is only one type of electrolyte in solution, the concentrations cancel as is the concentration of the electrolyte producing ion