¶ Potential
Electrostatic potential () is defined as the work required to move a positive charge from infinity to the point of interest
- Positive charge = repulsion of positive charge = high electrostatic potential
- Negative charge = attraction of positive charge = low electrostatic potential
Because in chemistry, it is the electron that is moving, so it may be easier to view it from the perspective of a negative charge
- We therefore define "Electron Energy" as the negative of Electrostatic Potential
The difference in electrostatic potential is the voltage
¶ Capacitor
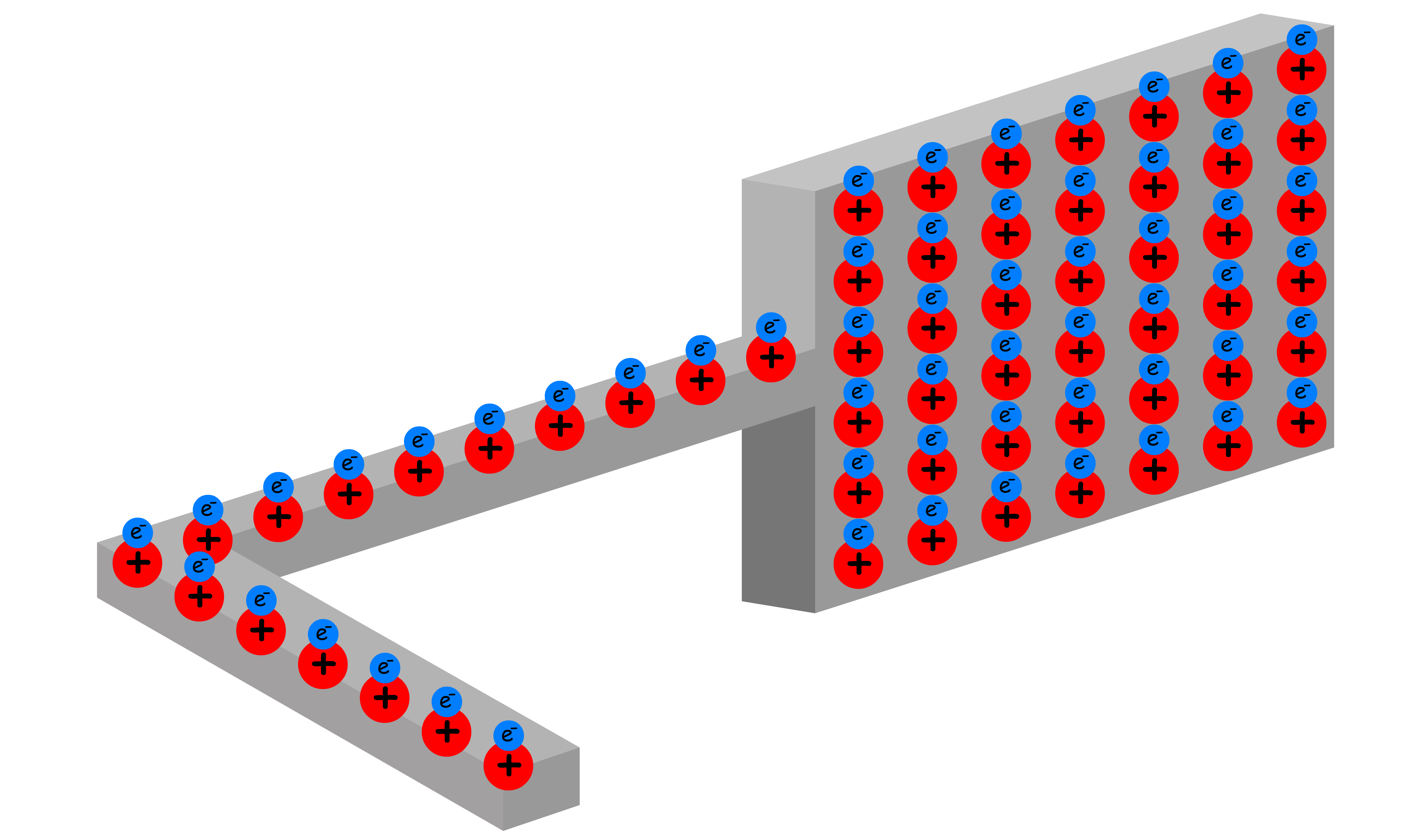
A capacitor is a device that stores charges
- A conductor typically has an equal number of protons and electrons, making it electrically neutral
- Even if we apply try to build up an excess charge on the plate by pushing the electrons with a force, the deviation in position of the electrons will result in a Columbic force that pushes the electrons in the opposite direction
Parallel Plates
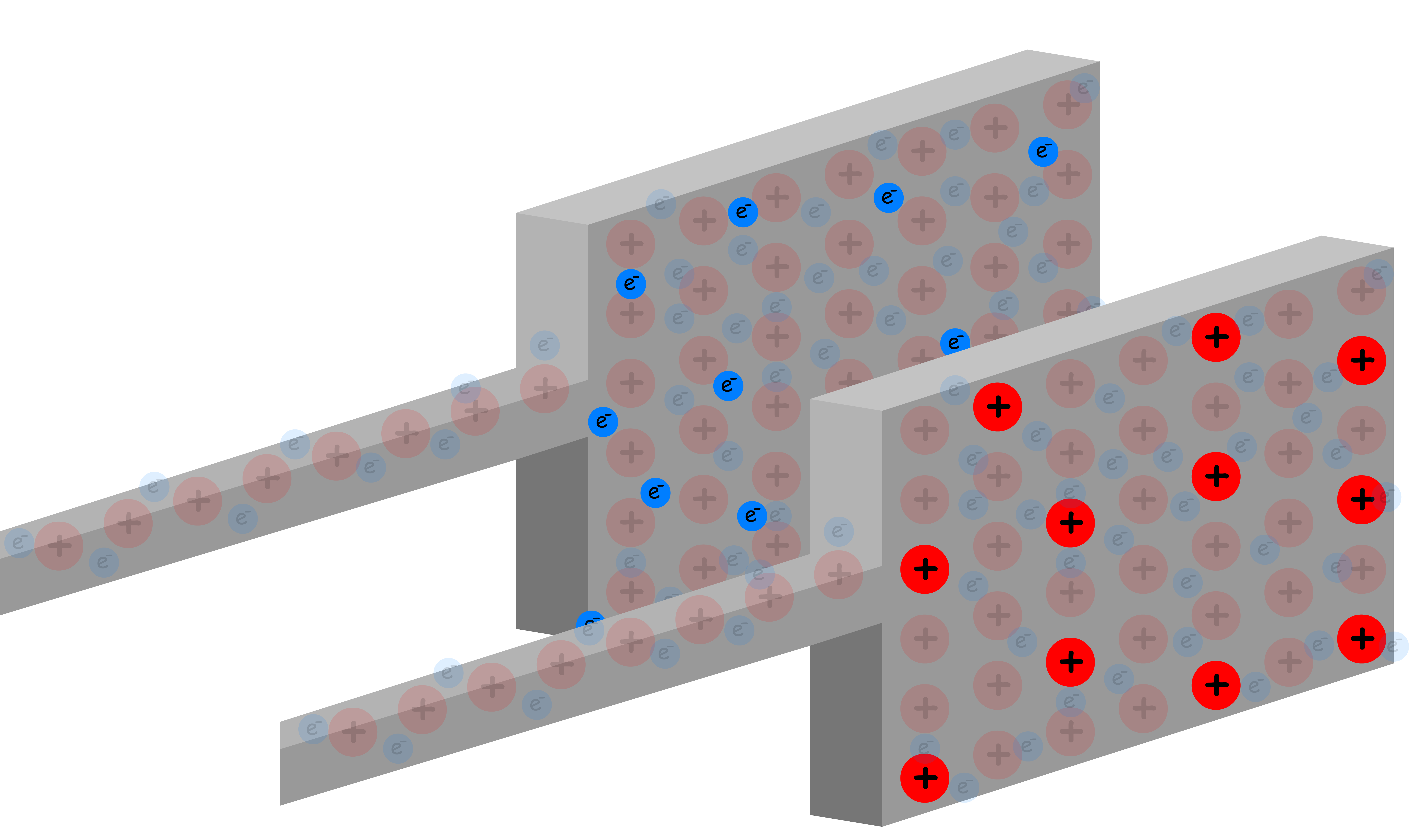
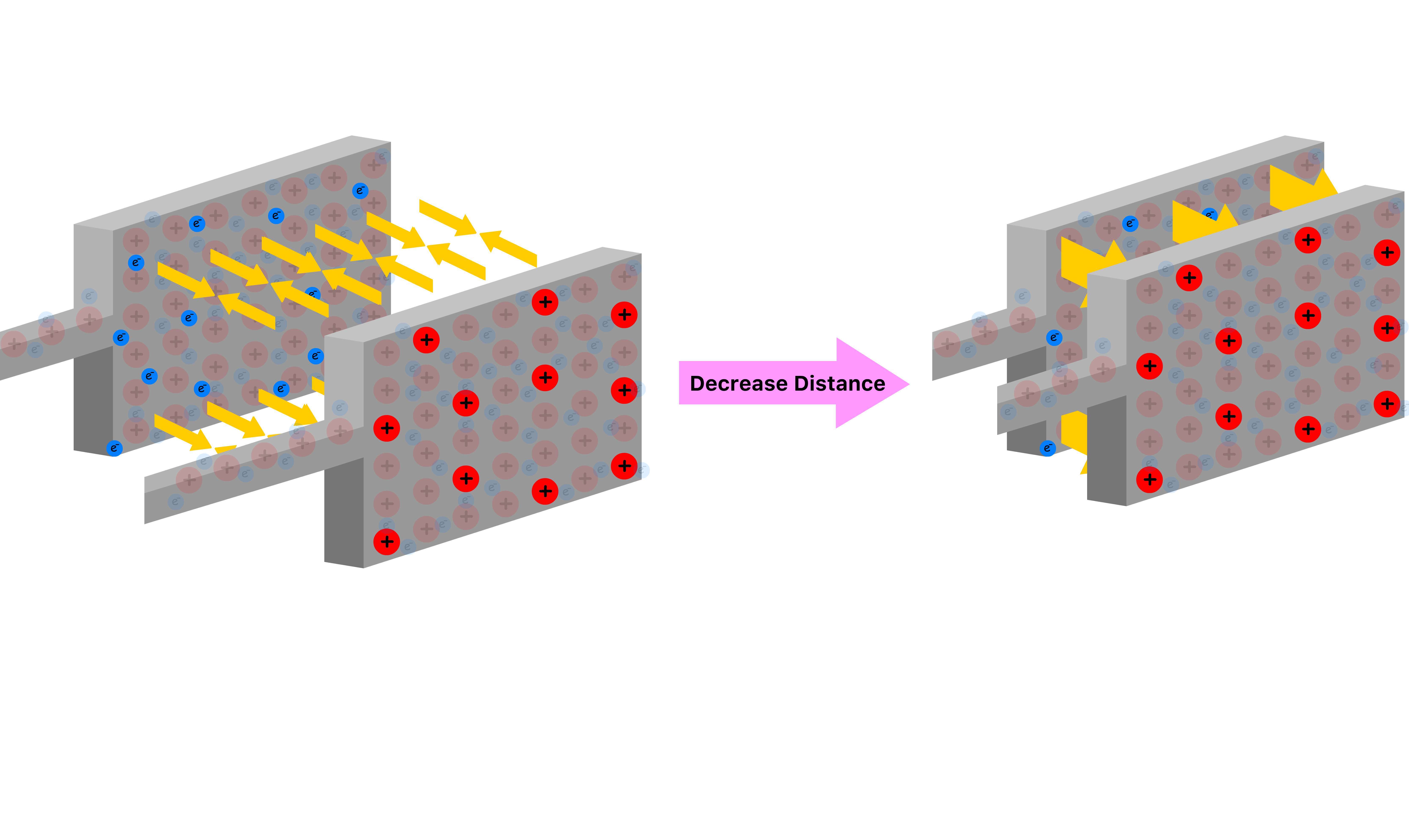
Let us now consider a new scenario where there is another plate close to the one shown
- As electrons accumulate in the one plate, they will repel the electrons in the other plate, causing it to have an excessive positive charge
- The two oppositely charged plates exert an attractive force on each other, making it possible for excess charges to accumulate on each of them
- As we add electrons to one plate, an equal number of electrons leave the other plate. This means that the charge of the two plates are opposite in sign, but same in magnitude
¶ Capacitance
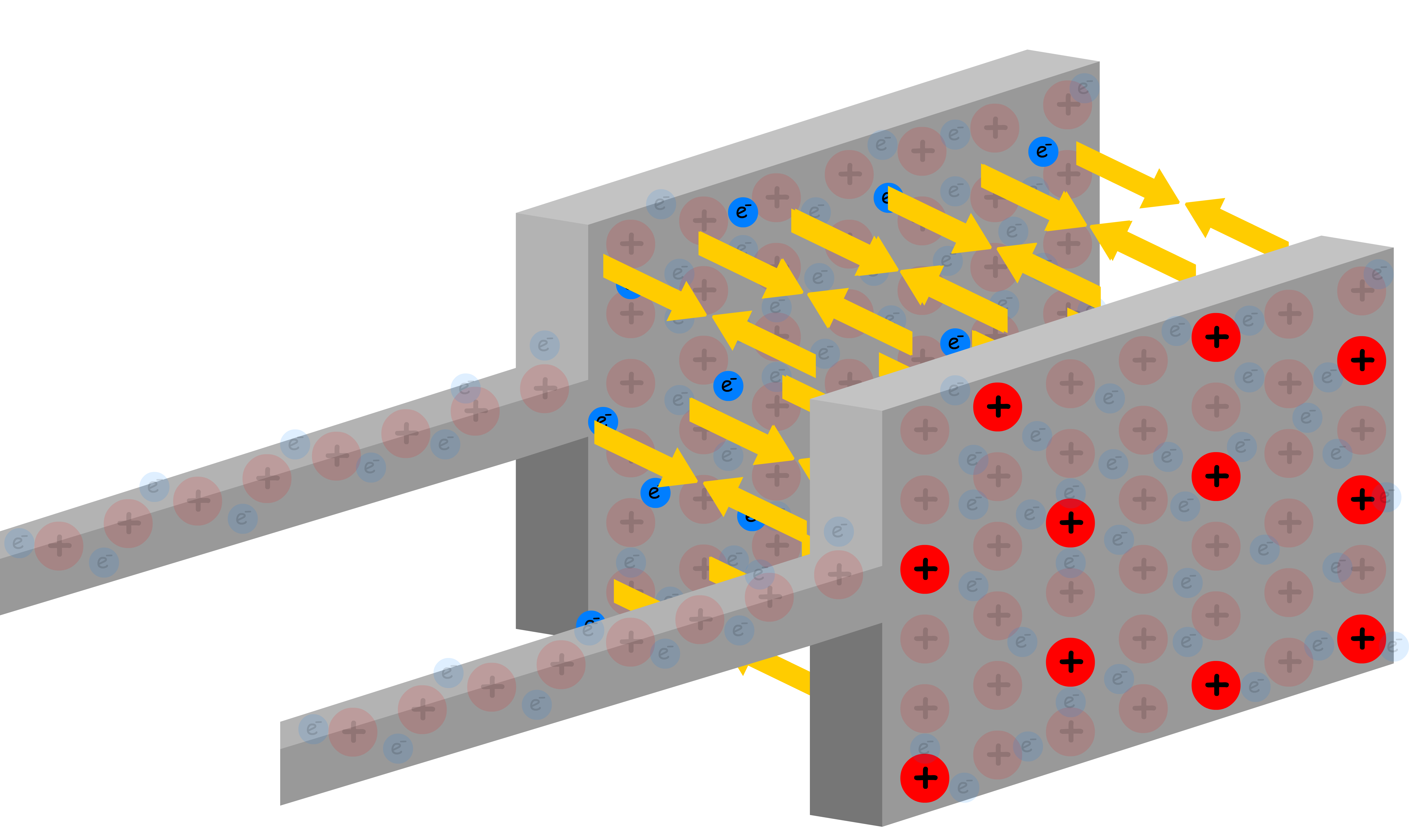
A larger charge will accumulate on each plate if the force used to push the electrons is larger
- In fact, the origin of such force is due to the potential difference between the two plates
- The proportionality constant is called the capacitance ()
Capacitance can be interpretted as the efficieny of the capacitor at accumulating excess charges
- Alternatively capacitance is the charge accumulated per potential difference of the capacitor
- The capacitance is independent of the voltage applied and it only depends on how the capacitor is constructed
Factors Affecting Capacitance
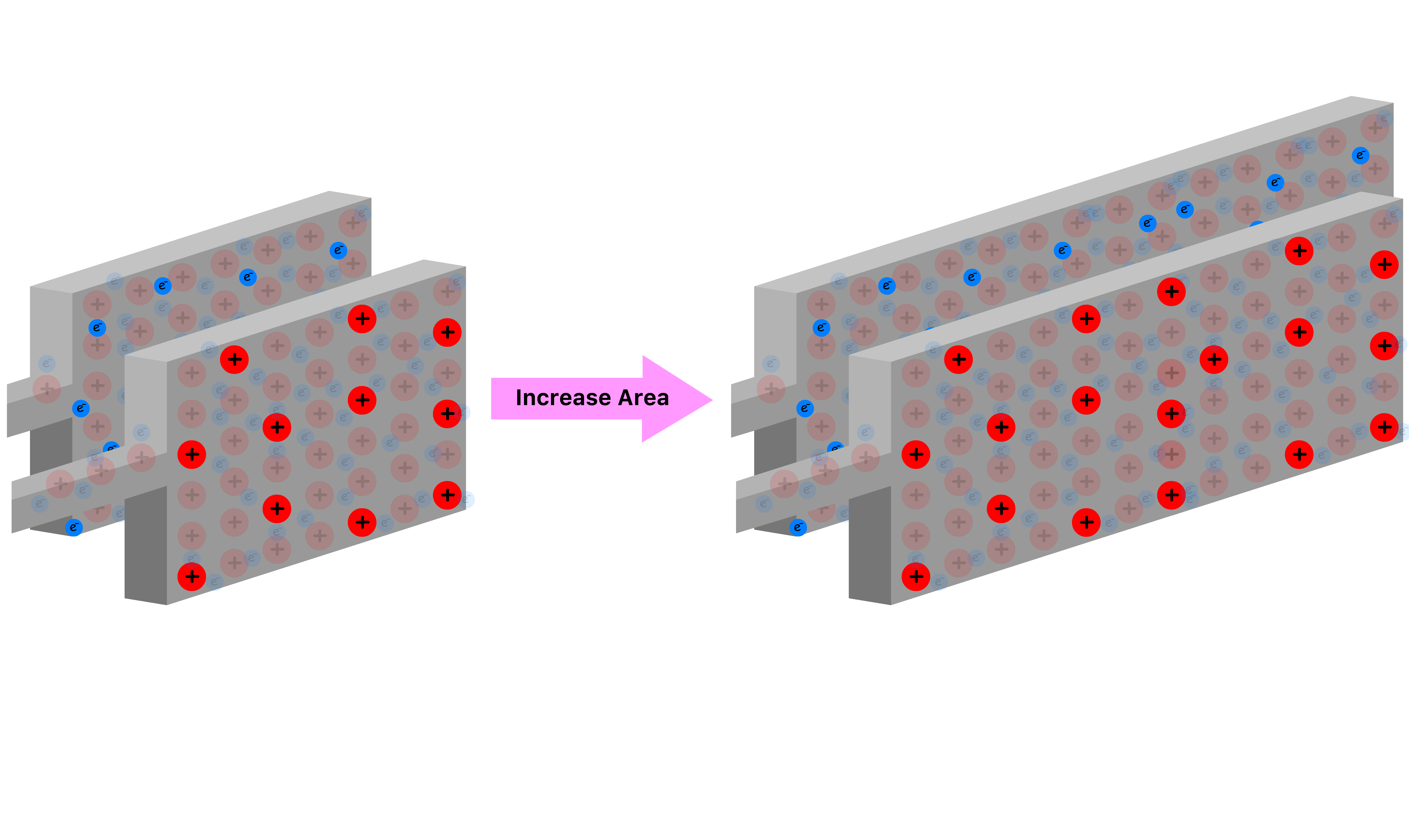
Suppose we increase the area of the plates
- The bigger the plates are, the more charge they can store because the charges can spread out more
- Hence, the capacitance is directly proportional to the area of the plate
Suppose we move the two plates closer to each other
- The decrease in distance causes the attractive Columbic force the plates exerts on each other to be greater, allowing the two plates to develop larger net charges for the same potential difference
- Hence, the capacitance is inversely proportional to the distance between the plates
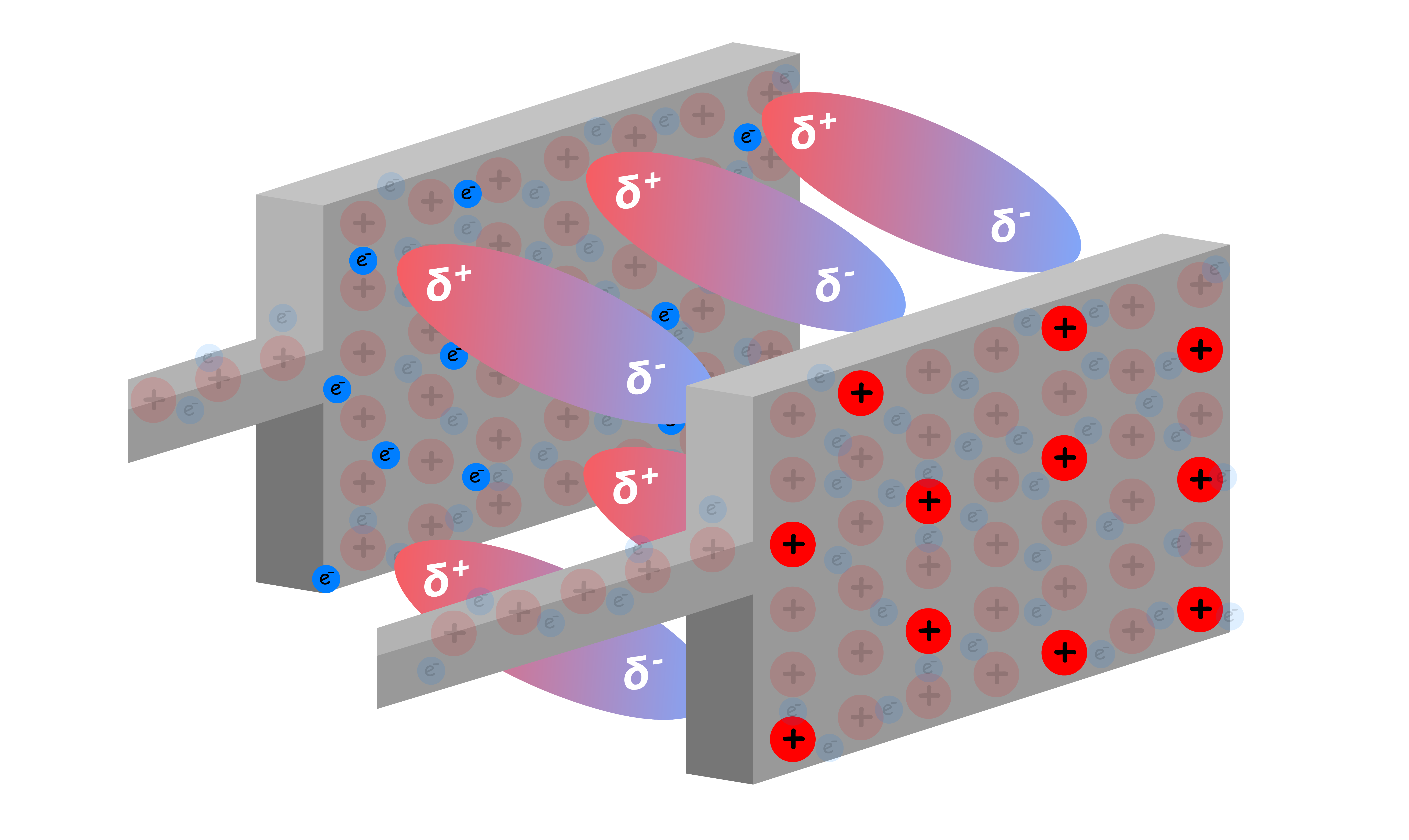
Instead of a vaccum, suppose we insert some insulator with a dipole between the plates
- This material does not allow any electrons to flow through it, but it contains molecules that change their orientation based on the charges of the two plates
- The Coulomb force between the closest ends of the molecules and the charge on the plates is attractive and very strong, since they are very close together. This attracts more charge onto the plates than if the space were empty and the opposite charges were a distance away
- Hence, the capacitance is directly proportional to the dielectric constant of the medium separating the two plates
Combining all the factors, the capacitance can be expressed as such
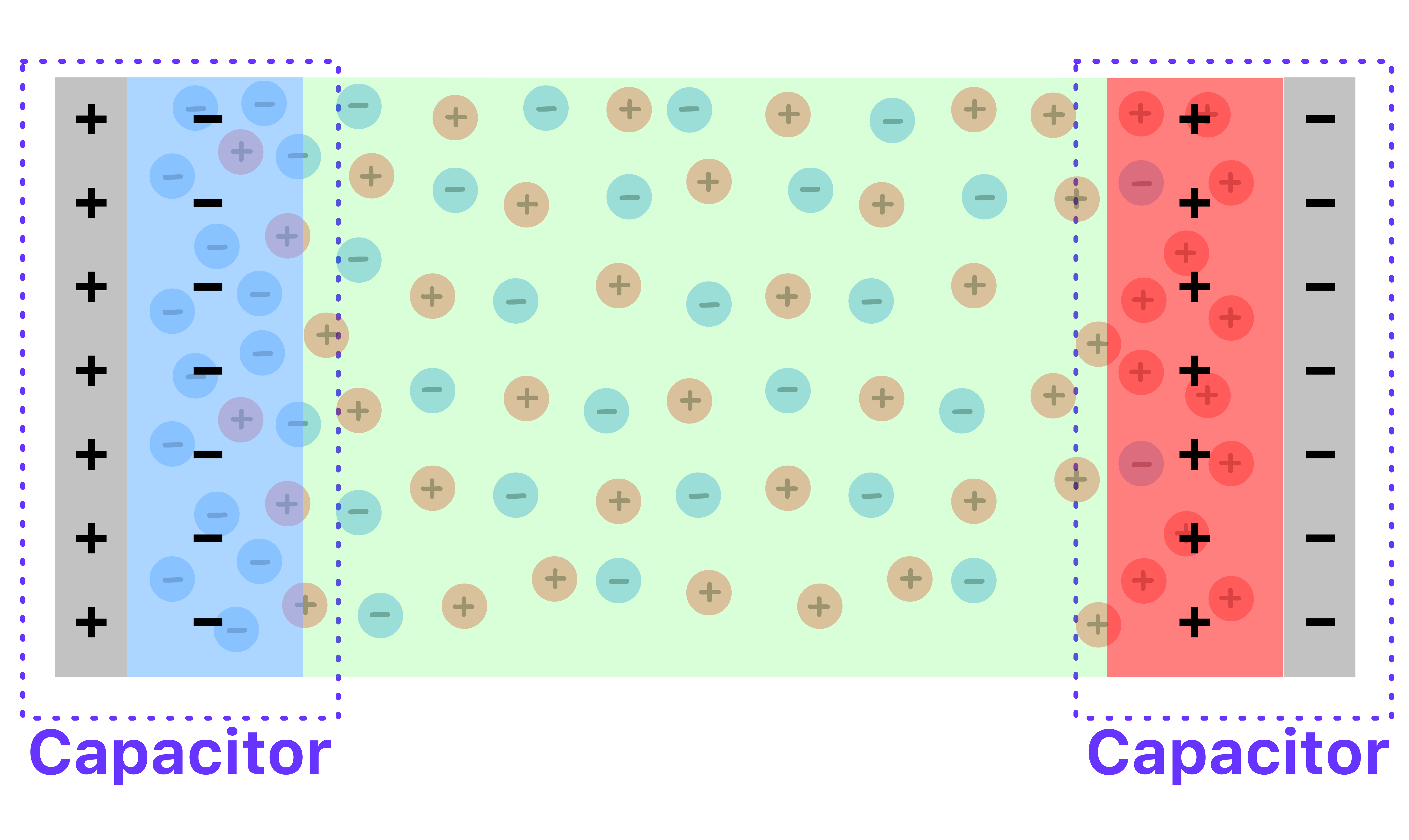
¶ Interfacial Capacitance due to Double Layers
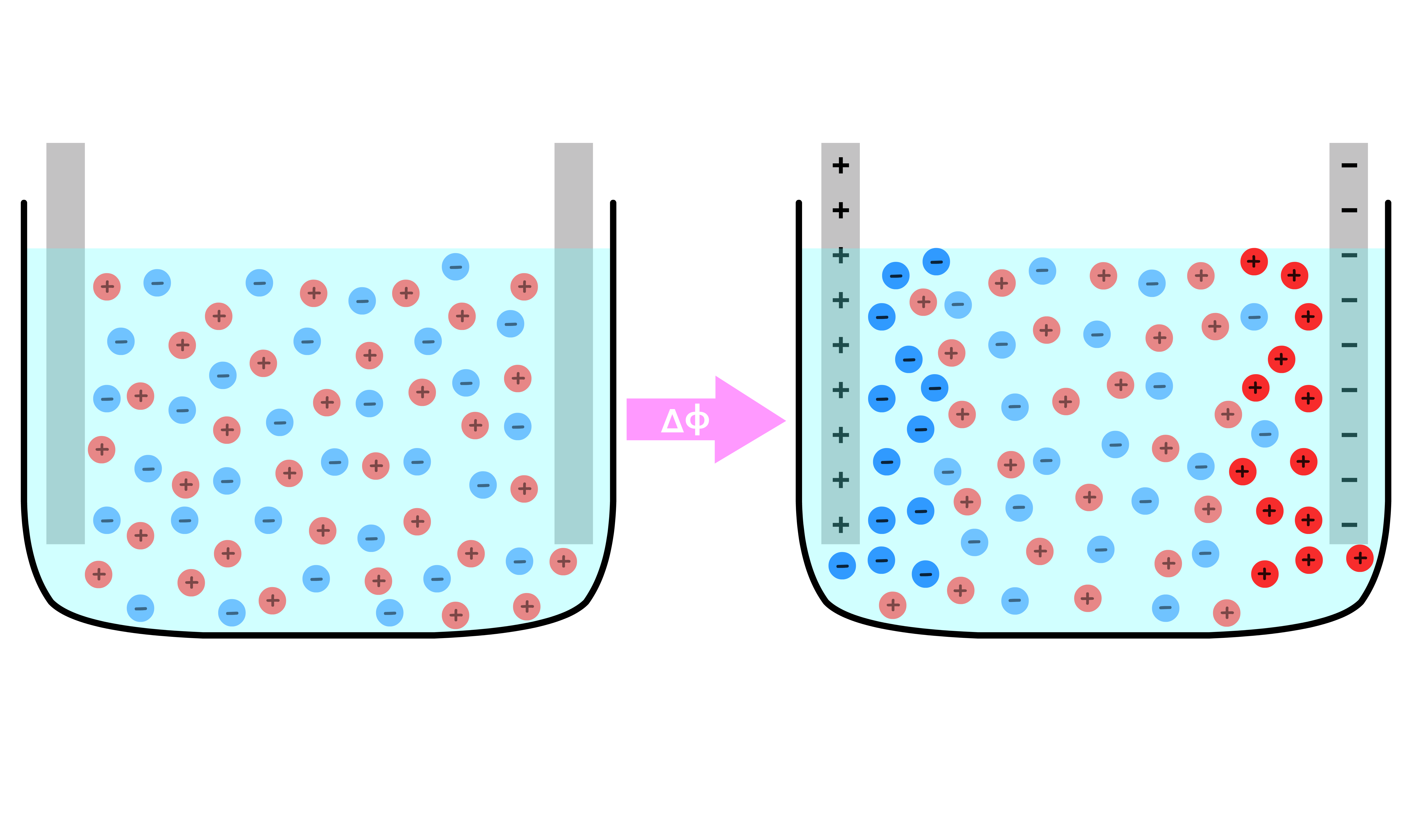
Something interesting happens when we use an electrolytic solution to separate the two plates
- Each ionic species will migrate towards the oppositely charged plate
- As a result, we end up with excess anions adjacent to the positive plate and excess cations adjacent to the negative plate
- Due to this distribution of charge, the potential does not change in the bulk of the material. Instead, all of the drop occurs within those narrow regions with a net charge
- In effect, the system contains two capacitor instead of one, one at each interface
Consequences
The capacitance is now independent of the plate separation
- The plate separation no longer represents the actual distance of potential drop
- The two capacitors only form at the interface of the plate, the separation of the bulk has no bearing on the capacitance
Increase in capacitance
- The effective separation within each capacitor is now the distance between the the plate and the narrow region of excessive charge, which is on the order of nanometers
- Since capacitance is inversely proportional to the separation, the capacitance increases
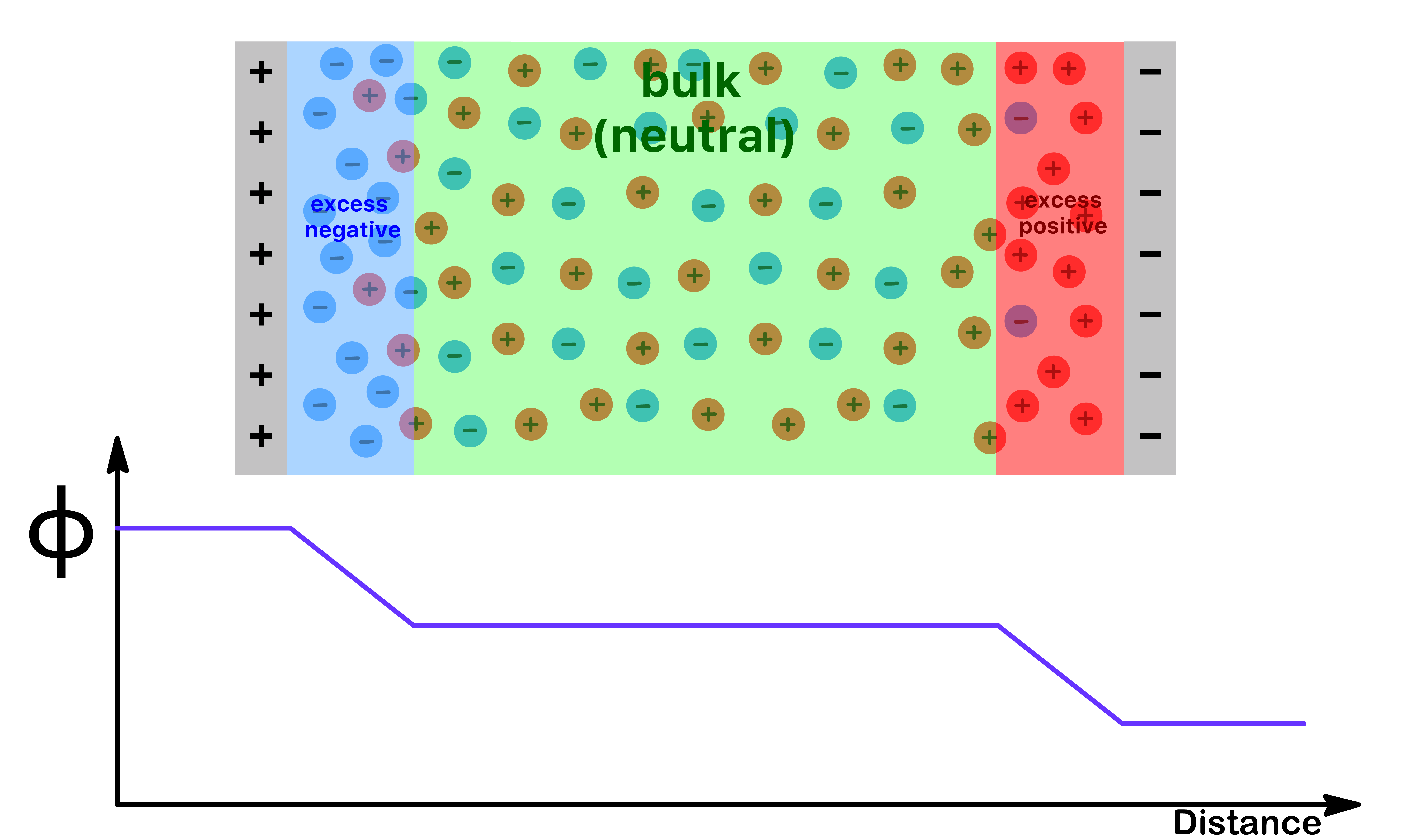
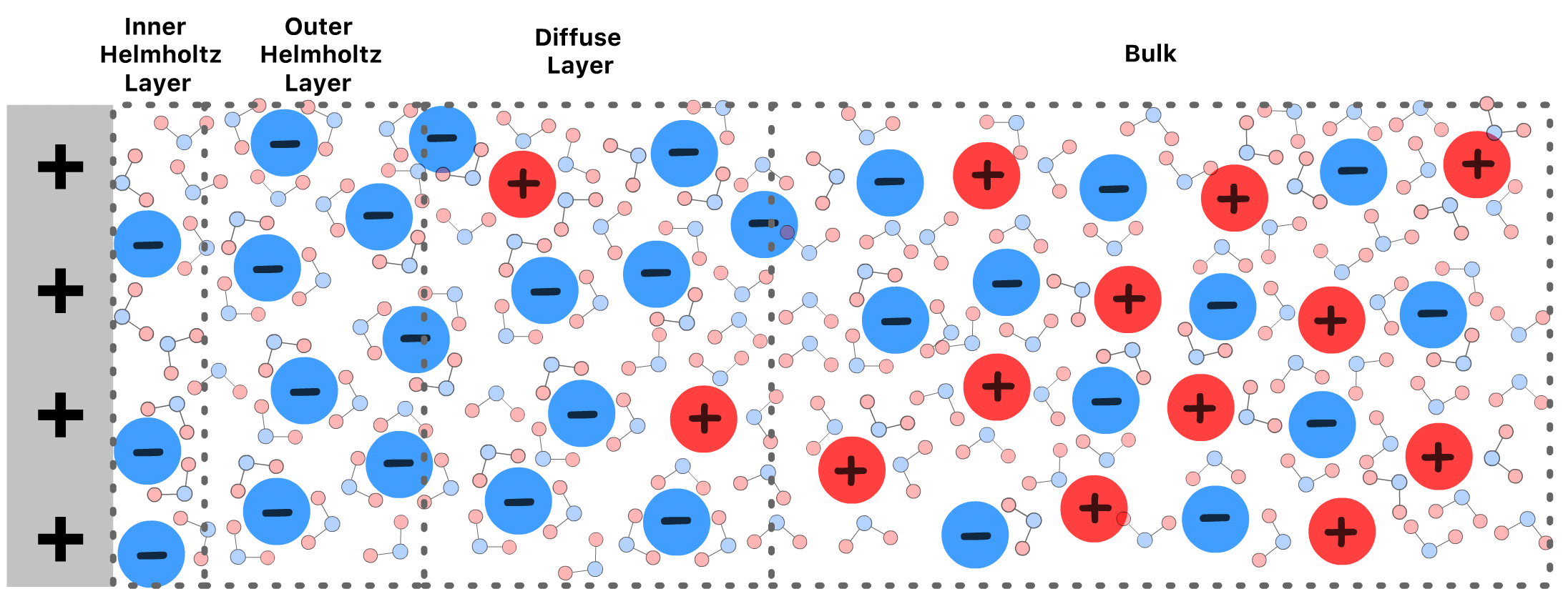
The Theory of Double Layer Structure
The distribution of charge within the double layer is not uniform and we can divide it into three layers
- The inner Helmholtz layer consists of ions which are adsorbed to the plate and have lost their solvation shells
- The inner Helmholtz layer is composed of ions which are adsorbed to the plate but are not in direct contact with it due to the presence of their solvation shells
- The diffuse layer is made of free ions that move in the fluid under the influence of electric attraction and thermal motion rather than being firmly anchored
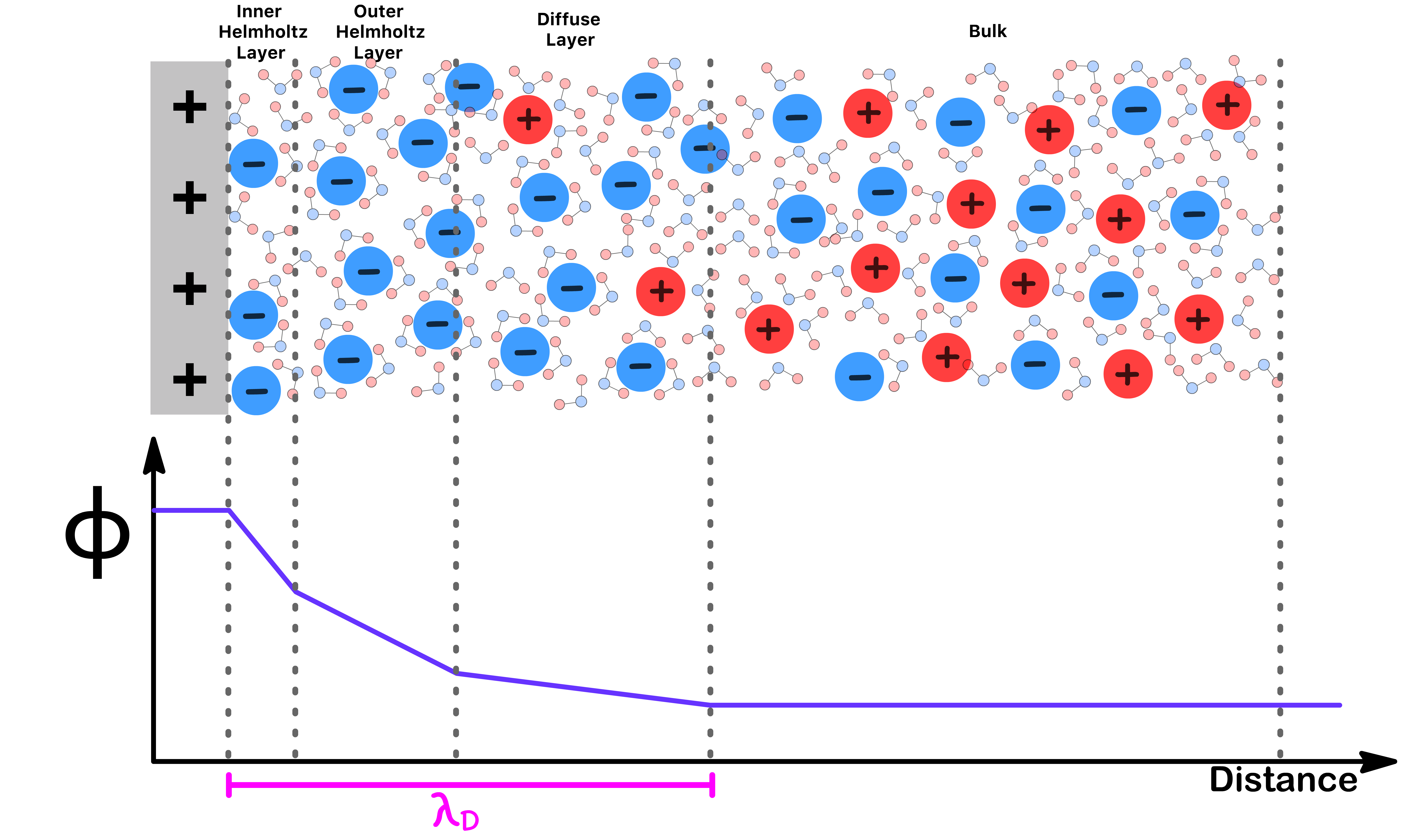
Due to the non-uniform ionic distribution, the potential change across the double layer also varys with distance
- The change in potential becomes less rapid as we move from the inner layer to the outer layer and to the diffuse layer
- The bulk is electrically neutal and therefore the potential remains constant at that layer
We can approximate the thickness of the region with an excess charge using the Debye Length,
- For every , the potential will decrease by ( i.e. ≈36.8% of its initial value)
- Since it depends mostly on ionic strength, increasing ionic strength reduces Debye length, which in turns makes the double layer thinner
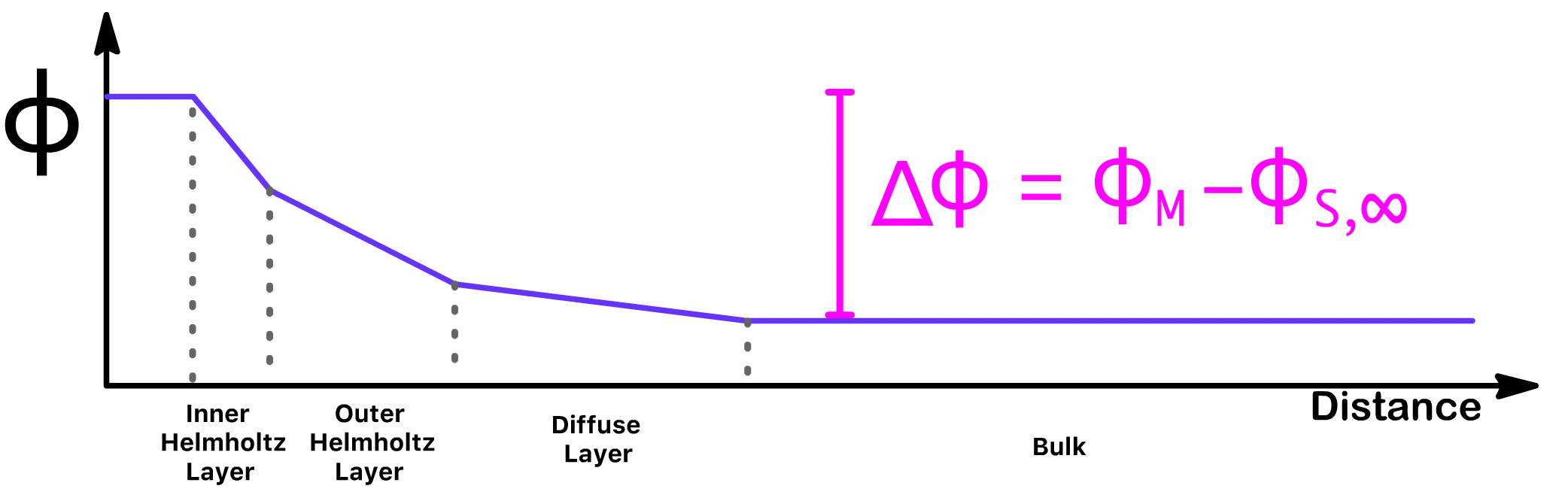
A capacitor does not exist without a potential difference, so it is important for us to define what the potential difference is in this situation
- We define the potential difference as the potential within the metal plate minus the potential of the bulk. We call this potential difference, the Galvani potential difference
- If the electrode is part of a cell from which no current is being drawn, the Galvani potential difference will become the Half-cell potential,
- The half-cell potential is also called the electrode potential
¶ Electron transfer at the Interface
If the half-cell potential, , is large enough we can induce electron transfer across that interface
- On contact between metal and solution, electron can lower its energy by moving from the molecules in solution to the metal or from the metal to the molecules in solution
- All electron transfers occur to/from the Fermi level
Since electrons are negatively charged, they want to go from a region of low potential ( high electron energy ) to a region of high potential ( low electron energy )
- When , electrons go from the solution to the metal. We call this oxidation
- When , electrons go from the metal to the solution. We call this reduction
¶ Half-reaction and Full reaction
The concept of reduction half equation is crucial in electrochemistry
- The general reduction half equation can be expressed as such
Any redox equation can be expressed as the difference of two reduction half-reactions
- This works because the negative of a reduction half-equation is just a oxidation half-equation
- This is important because we can relate the properties of half-reactions in a similar manner
These relations are written with the following assumptions:
- The right-hand side is the cathode and the left-hand side is the anode
- The value of the parameters are given in terms of the reduction half-reaction
The cell potential does not depend on the number of electrons transferred in the overall reaction. This is because when we measure the potential of a cell, current is not actually flowing (no net chemistry occurs)
- It is therefore essential to realize that we should not scale the reduction potential even when we are scaling the half reactions to balance the equations
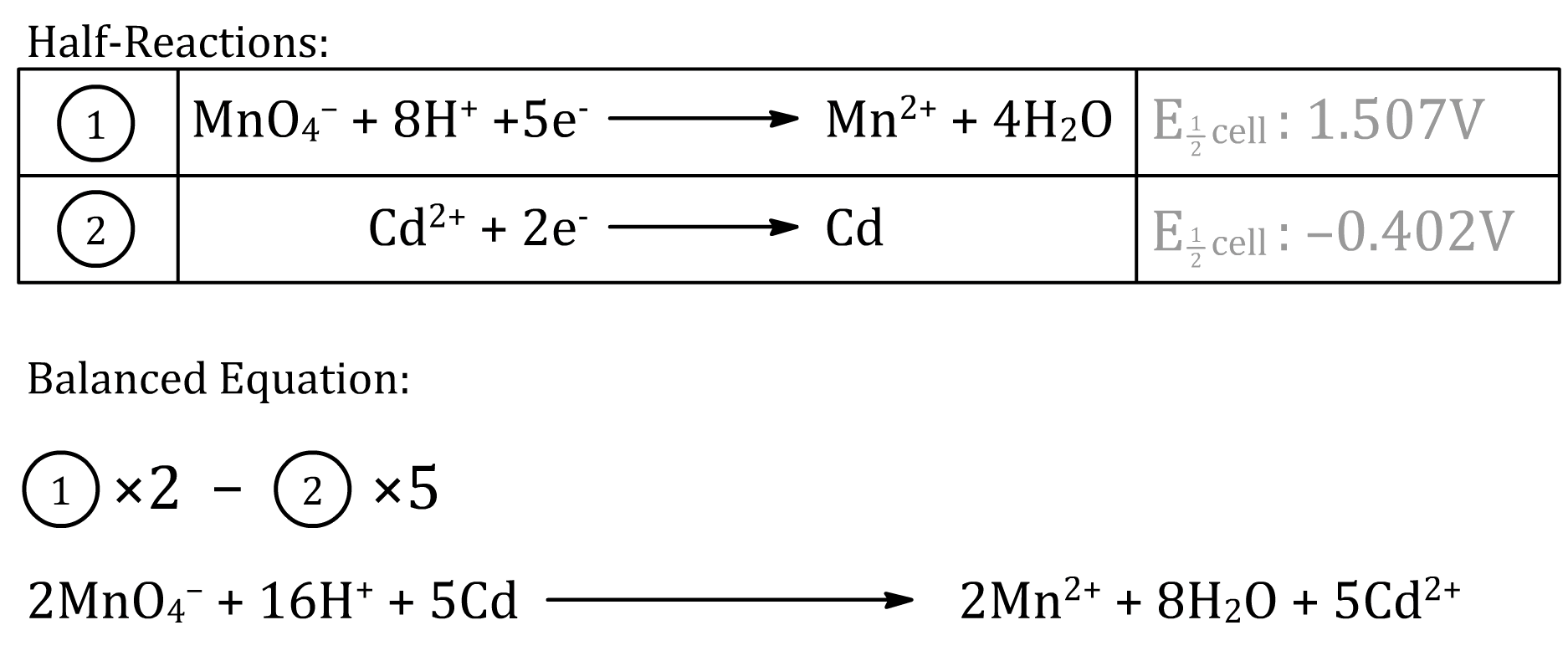
Example:
Common Mistake
Correct Answer
¶ Electrochemical potential
The electrochemical potential of a species is define as the chemical potential of said species plus an extra energy term associated with ions in electrical potential
- The Avogadro's constant is included because electrochemical potential is molar
Using this definition, we can express the electrochemical potential for an arbitrary chemical species, , as such
- For a species in solution, the potential is the potential in the bulk
- Since we prefer to write half-reactions as reductions (even when they are oxidations), we are always assuming that the electron came from the metal plate. Hence, the potential of the electron is the potential of the metal plate
Relating Potential to Gibbs Energy
Assume a reaction:
- At equilibrium the electrochemical potential of reactants and products are the same, such that
- We can then expand each electrochemical potential in terms of their respective expressions
- With some algebaric manipulation, we will get
- We therefore obtain the relation, where is the number of electrons after balancing both half reactions
- We can write something similar for the full redox reaction
¶ Galvanic and Electrolytic Cell
In dynamic electrochemistry, electrons are removed from, or given up to, species in solution and this process results in a change in energy
- If energy has to be provided by an external power supply to drive the reactions then the electrochemical cell is referred to as an electrolytic cell
- If the reactions occur spontaneously, then the cell is referred to as a Galvanic cell
Line Notation
A shorthand method for describing electrochemical cells is to use line notation
- The convention is to write the anode reaction at the extreme left-hand side and the cathode reaction at the right-hand side
- A single line ‘|’ indicates a phase boundary while a double vertical line ‘||’ indicates a salt bridge
¶ Changing of reaction direction
Having established the relation between the reaction Gibbs energy and the cell potential, we can predict the spontaneity of a process simply by examining the sign of the cell potential
- Recall that the sign and value of the reaction Gibbs energy dictates the spontaneity of a process
- Since the cell potential is directly proportional to the negative of the reaction Gibbs energy, we can say
Just pick up any phys chem book if you don't believe me
¶ Nernst equation
We can go on to relate the cell potential to the concentration / activities of the species in the cell reaction
- We know that reaction Gibbs energy is related to the composition of the reaction
- Division of both sides by gives us
- By recognizing the relation between cell potential and reaction Gibbs energy, we will arrive at the Nernst Equation
The Nernst equation gives us the dependence of the cell potential on the composition of the reaction mixture
The Nernst equation is just the disguised form of , so we can draw a lot of similar conclusions
- is analogous to , in the sense that they are used to predict the direction of a reaction
- is analogous to , in the sense that they are used to determine the composition of the reaction mixture at equilibrium:
¶ Measuring Half-potential
It is not possible to measure a half-cell reaction on its own, so we shall define the potential of one of the electrode as zero
- We take the convention that the half-cell potential of a standard hydrogen electrode (SHE) as 0 at all temperature
- The standard potential of any electrode can then be assigned by constructing a cell where the LHS electrode is the SHE and the RHS electrode is the electrode of interest
- As established before, the cell potential is defined to be the RHS half-cell potential minus the LHS half-cell potential
- Since the LHS electrode is the SHE, it is by definition 0V. Hence, the overall standard cell potential of such a cell is equal to the RHS half-cell potential