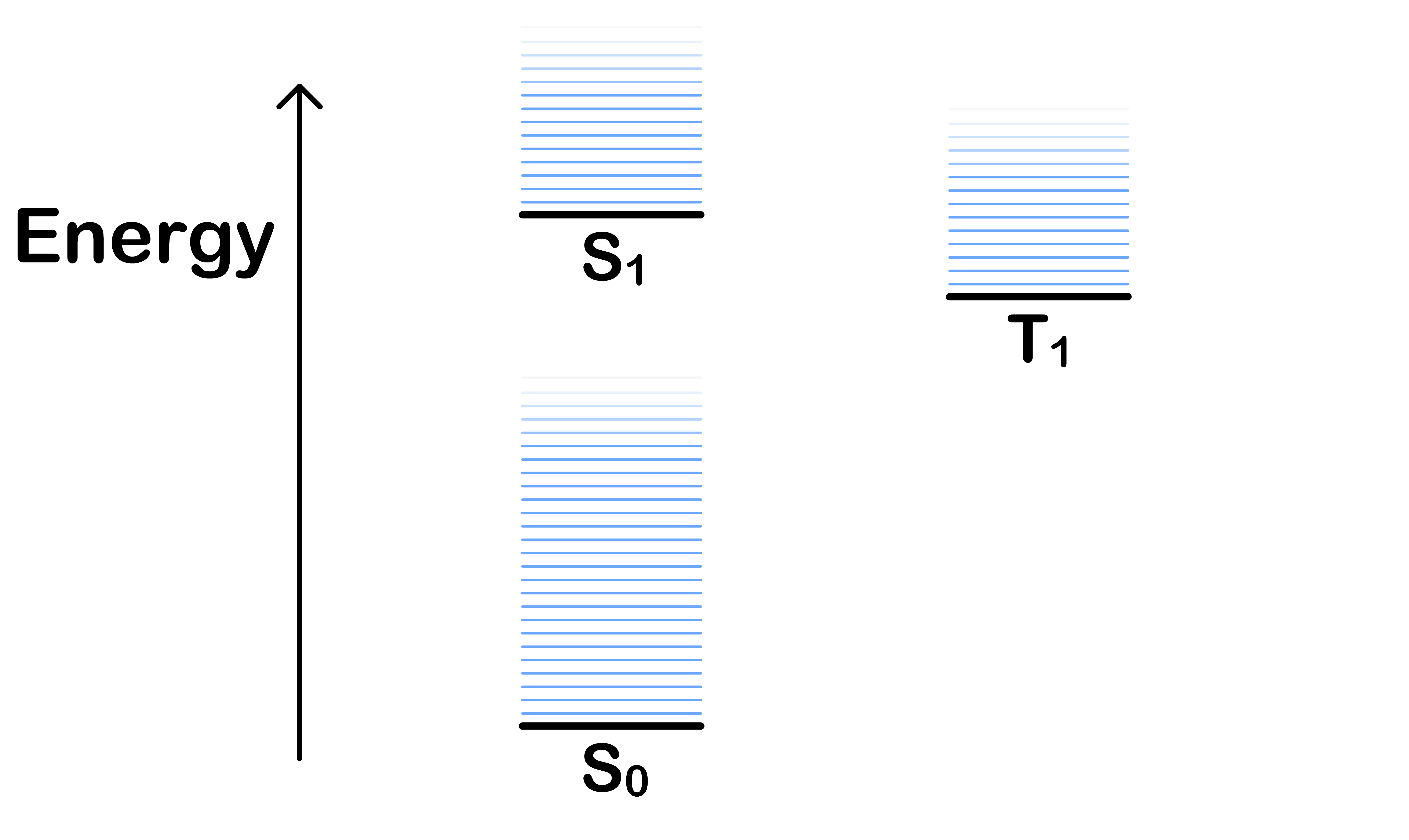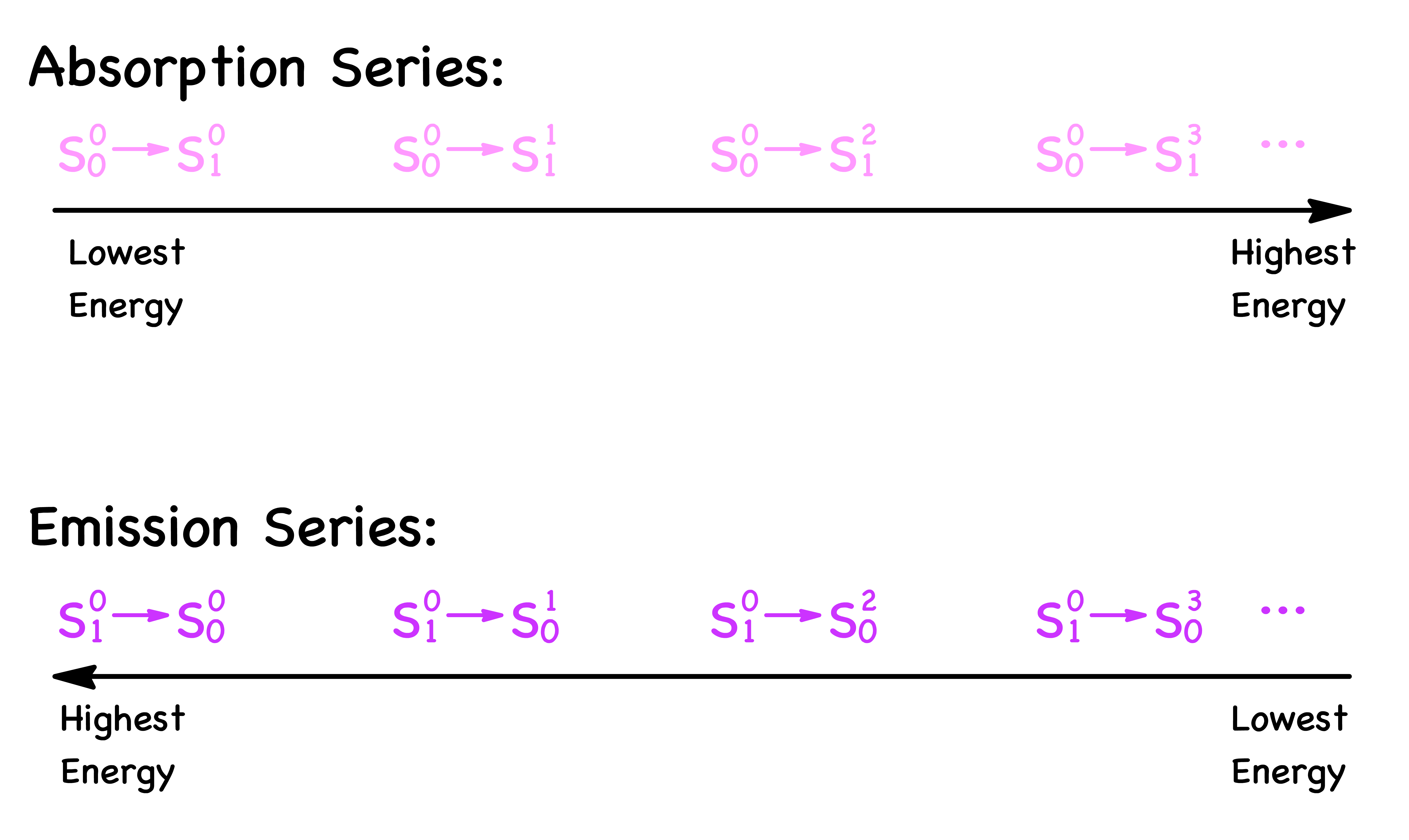¶ Read me / Recap
An extremely important concept in photochemistry (or quantum chemistry in general) is inner product,
- The rest of the notes will be extremely intuitive once you understand the geometric / physical meaning of inner produt
A detailed explanation and derivation of inner product is provided in the math sections
- Introduces Dot product : Euclidean Vectors
- Introduces Operators : Linear Transformations
- Introduces Inner product and Dirac notation : Abstract Vector Space
For our purposes, understanding what dot product is will suffice
¶ Recap on Inner Products
For those who don't want to read the thorough explanation of what inner product is, here is a brief summary of inner product
- However, I STRONGLY RECOMMEND you to read the actual derivation as it will greatly assist your learning
The inner product is a generalized version of dot product
- Physically, it measures how much vector and vector overlaps in space
- Alternatively, we can think of it as a measure of how similar vector and vector are
- This notion can be applied directly to functions (as functions are just a special type of vectors, but there is no reason to go down that rabbit hole right now)
The magnitude of inner product tells us how similar two vectors/ functions are
- Since inner product is a measure of similarity/overlap, its output must be nothing but a number
- The magnitude of this number is large when the similarity/overlap is large
- The magnitude of this number is small when the similarity/overlap is small
An important concept of inner product is orthogonality and normalization
- When two vectors/ functions are orthogonal to each other, then their inner product must be 0
- The inner product of the same vector must be 1 if said vector is normalized
¶ Basic Photophysics
¶ Electronic States
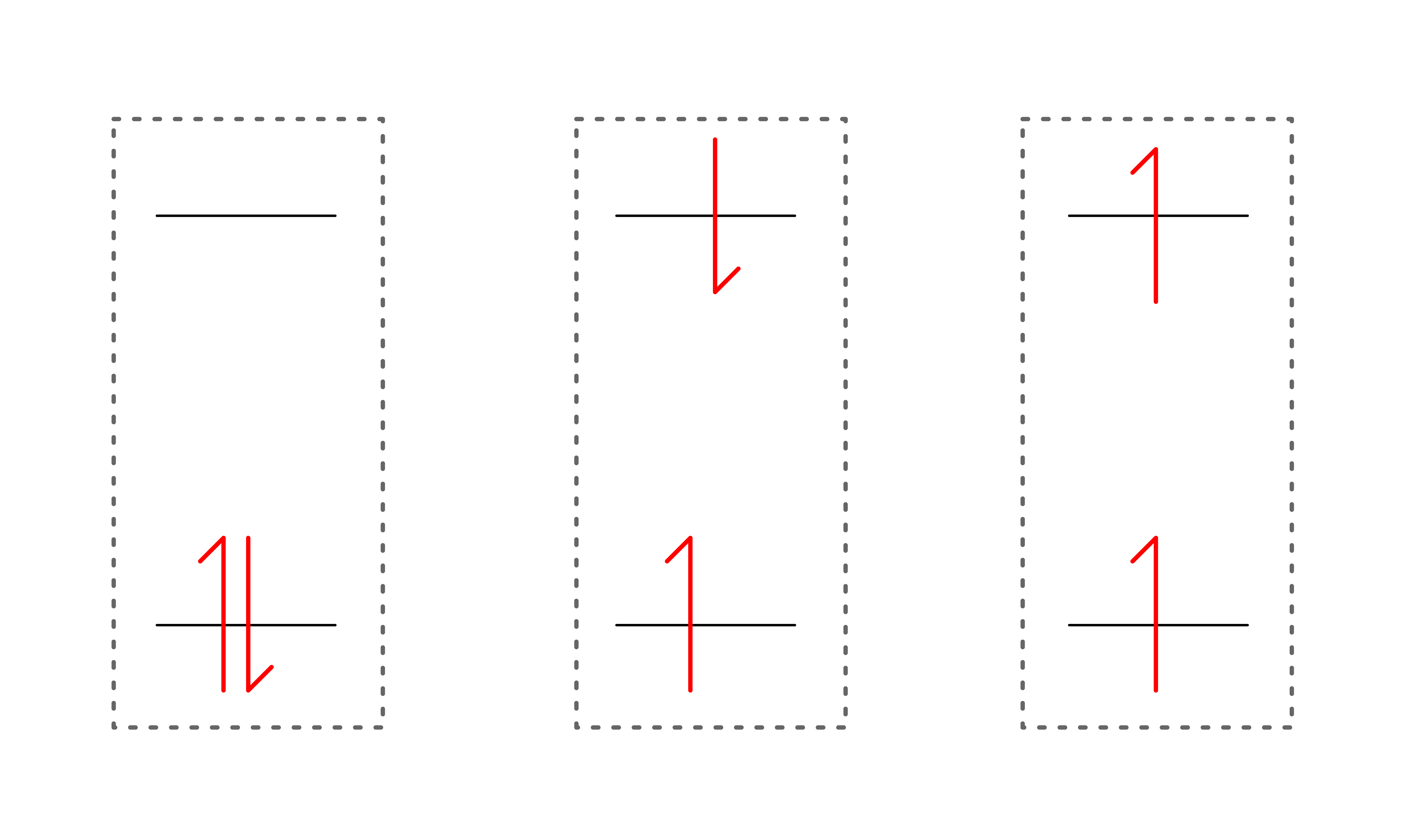
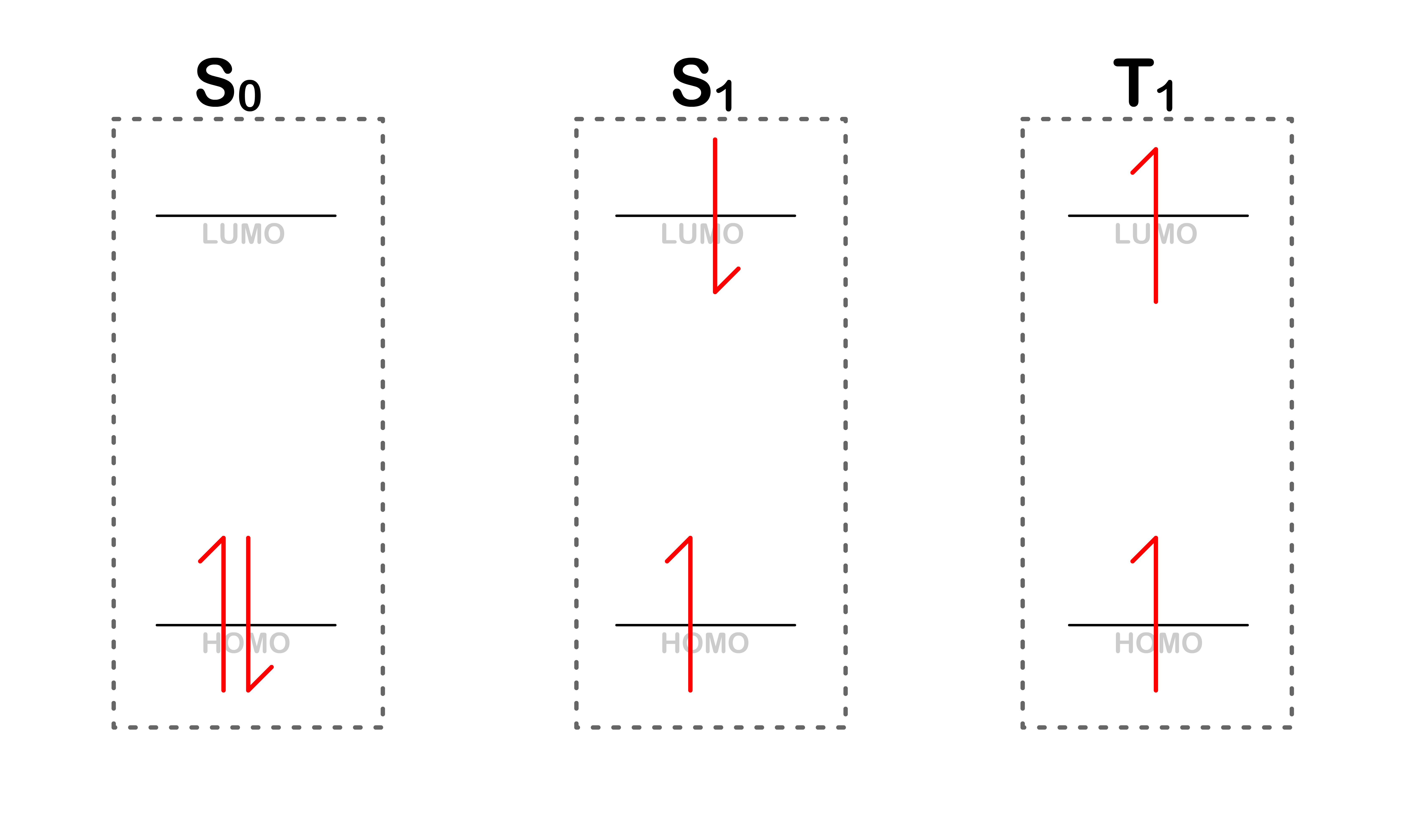
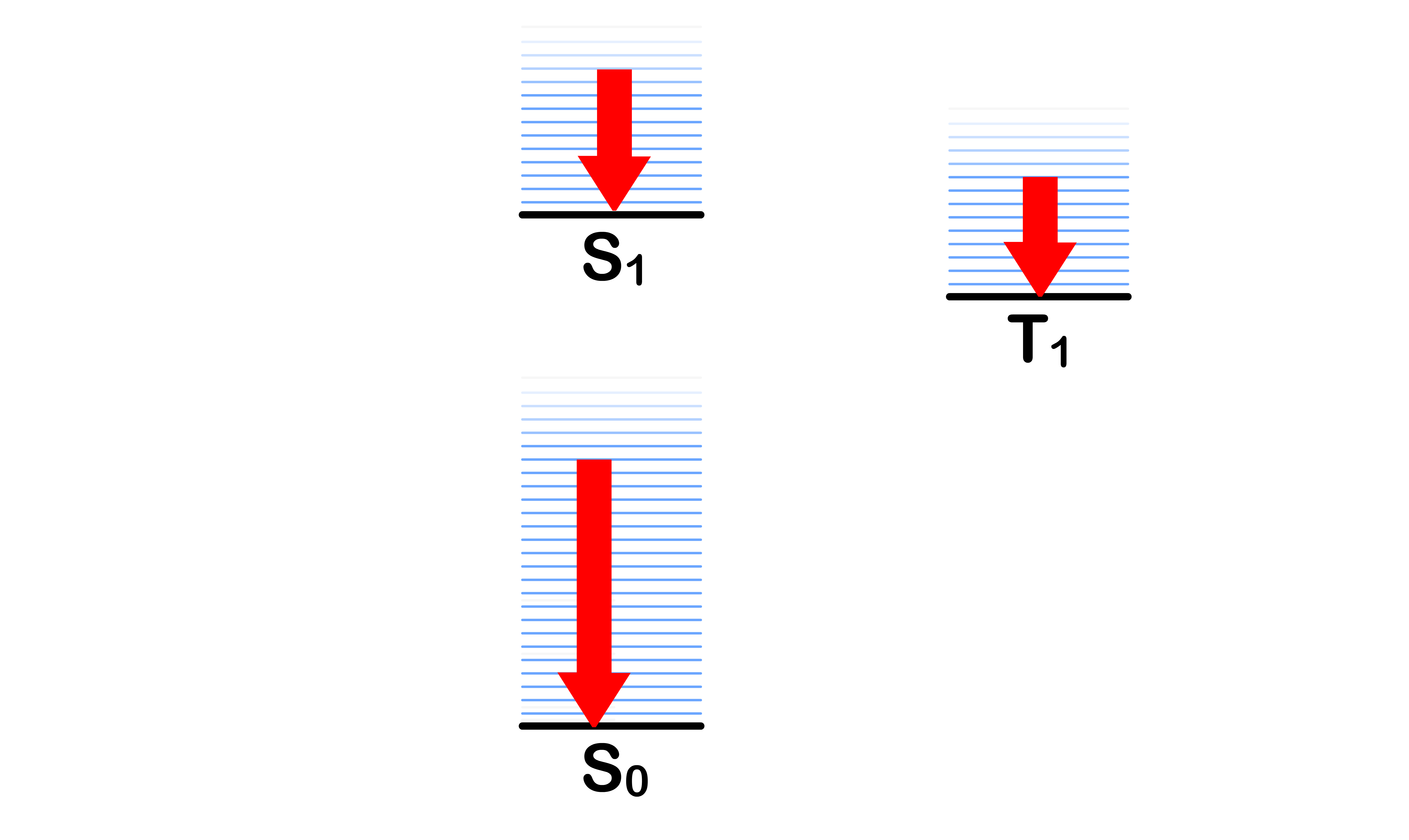
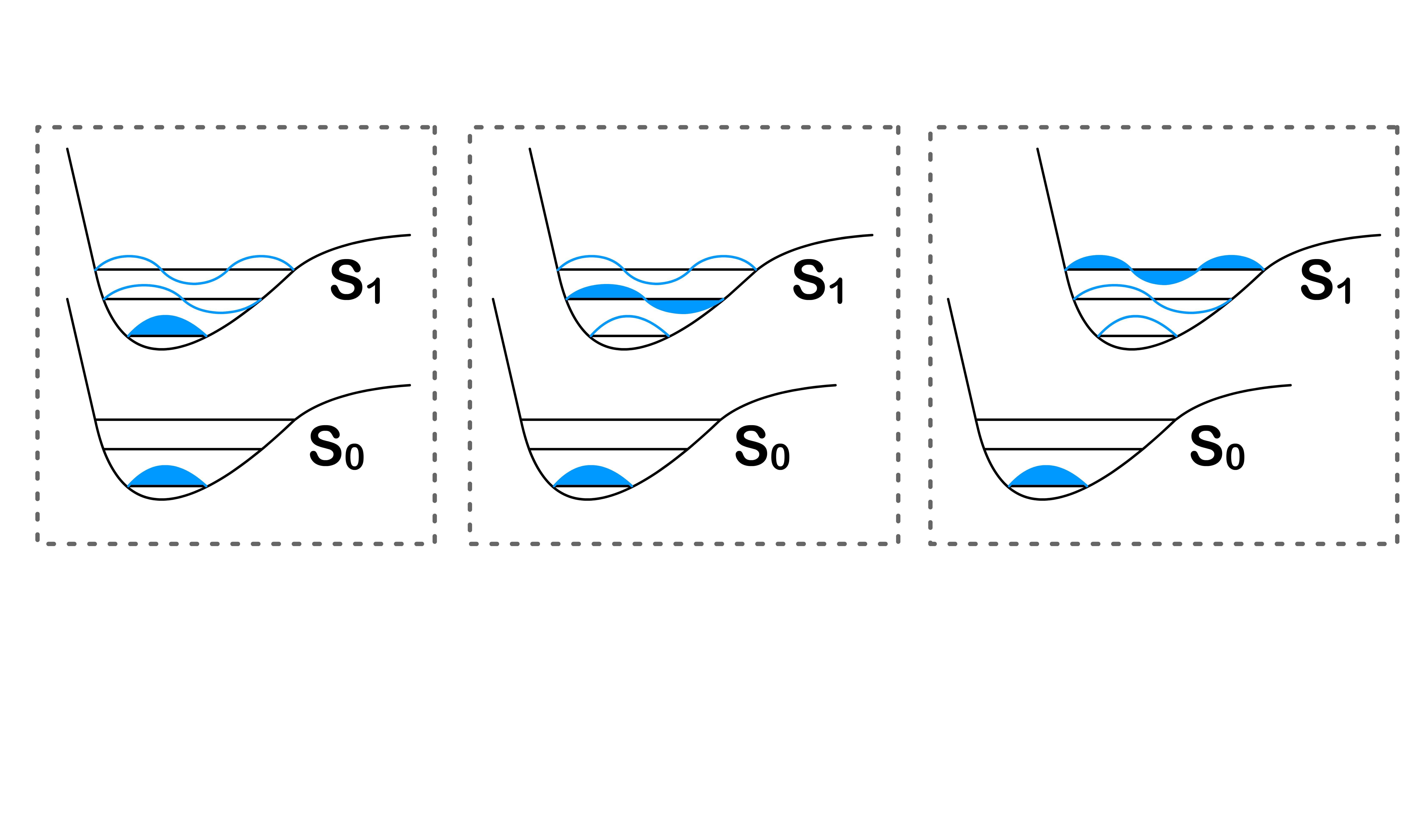
Consider the following situations
- Even though they all share the same orbital energy levels, it should be obvious that total energy of each of system is different
- For simplicity's sake, we shall name each of the situation
Each of these situation are simply different possible state a molecule can adopt
- It should be obvious why is lowest in energy, but what about and . To understand that, we shall look at the Pauli Exclusion Principle
Why triplet state (parallel spin) is lower in energy than singlet state (opposite spin)
- The Pauli Exclusion Principle states that two electrons cannot have the same set of quantum numbers (, , , )
- The first three quantum numbers describe the spatial position of the electron, while the last quantum number () describes the spin state of the electron
Consider the two possible situations, where we have two electrons
- The two electrons have the same spin state (triplet state)
- In this case, in order to obey the Exclusion principle, the spatial position of the two electrons must not be the same
- The two electrons have the different spin state (singlet state)
- The Exclusion principle has already been fufilled, so it is possible for the two electrons to share the same spatial position
When the electrons have the same spin, they must not be in the same space. But when they have different spin, it is possible for them to be in the same position
- Obviously, the electronic repulsion is greater when the electrons are closer together
- Hence, on average, the electrons with different spin will experience a greater Columbic repulsion and will therefore be higher in energy
- In other words, the singlet state (different spin state) is higher in energy than the triplet state (same spin state)
¶ Jablonski Diagram
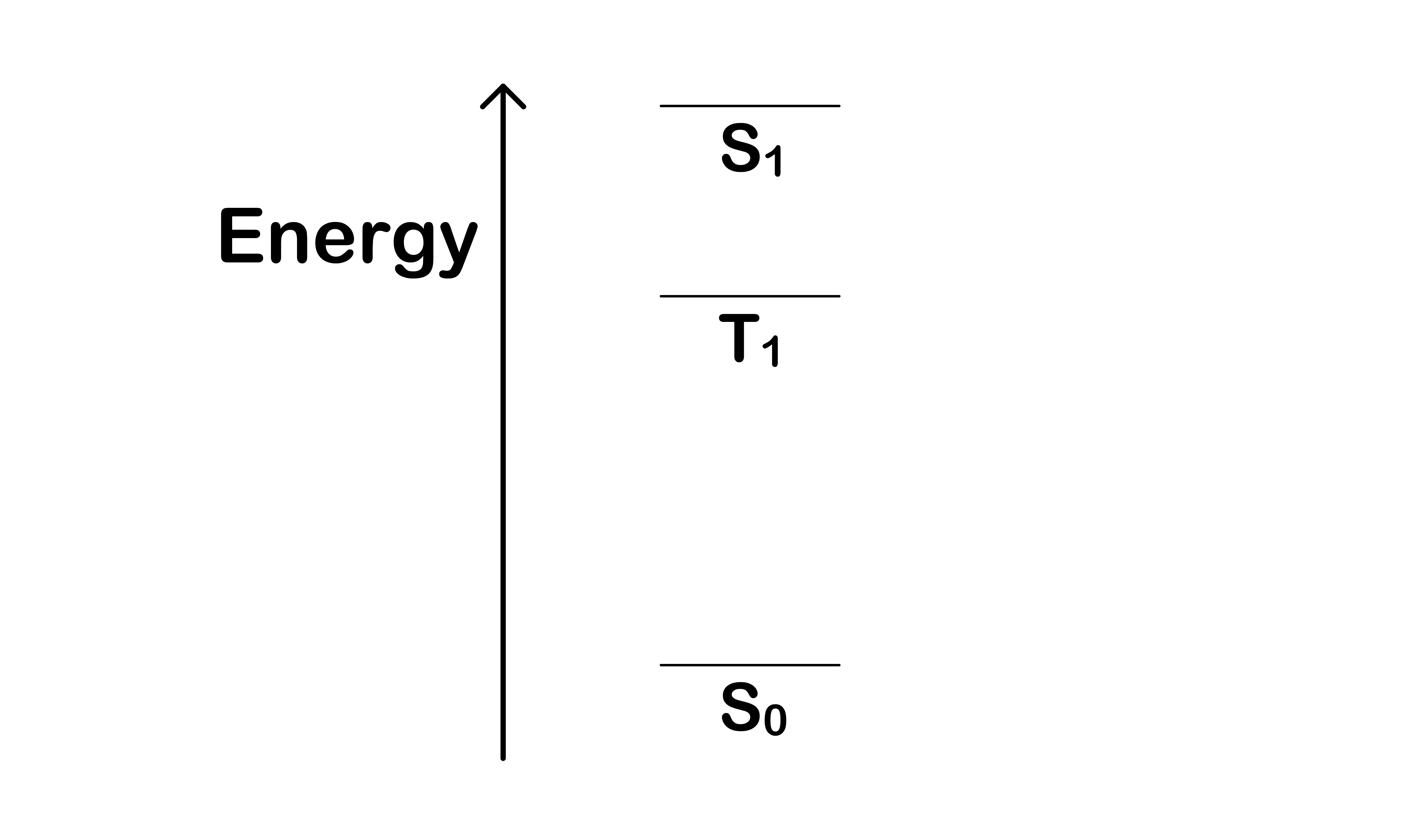
The Jablonski Diagram shows all the possible state a molecule can adopt
- We have introduced the three electronic states, , and
- For each electronic state, the molecule can have different vibrational modes, which causes the energy of the system to be different even though the electron configuration is the same
- We therefore overlay a series of vibronic states on each electronic state
A molecule can change from one state to another through different process
¶ Processes that do not involve photons
Vibronic Relaxation
- Decaying from an excited vibronic state to the ground vibronic state of the same electronic state
- Vibronic relaxation ensures that the other processes almost always begin from the ground vibronic state
- This will be explained in the Fermi Golden's Rule
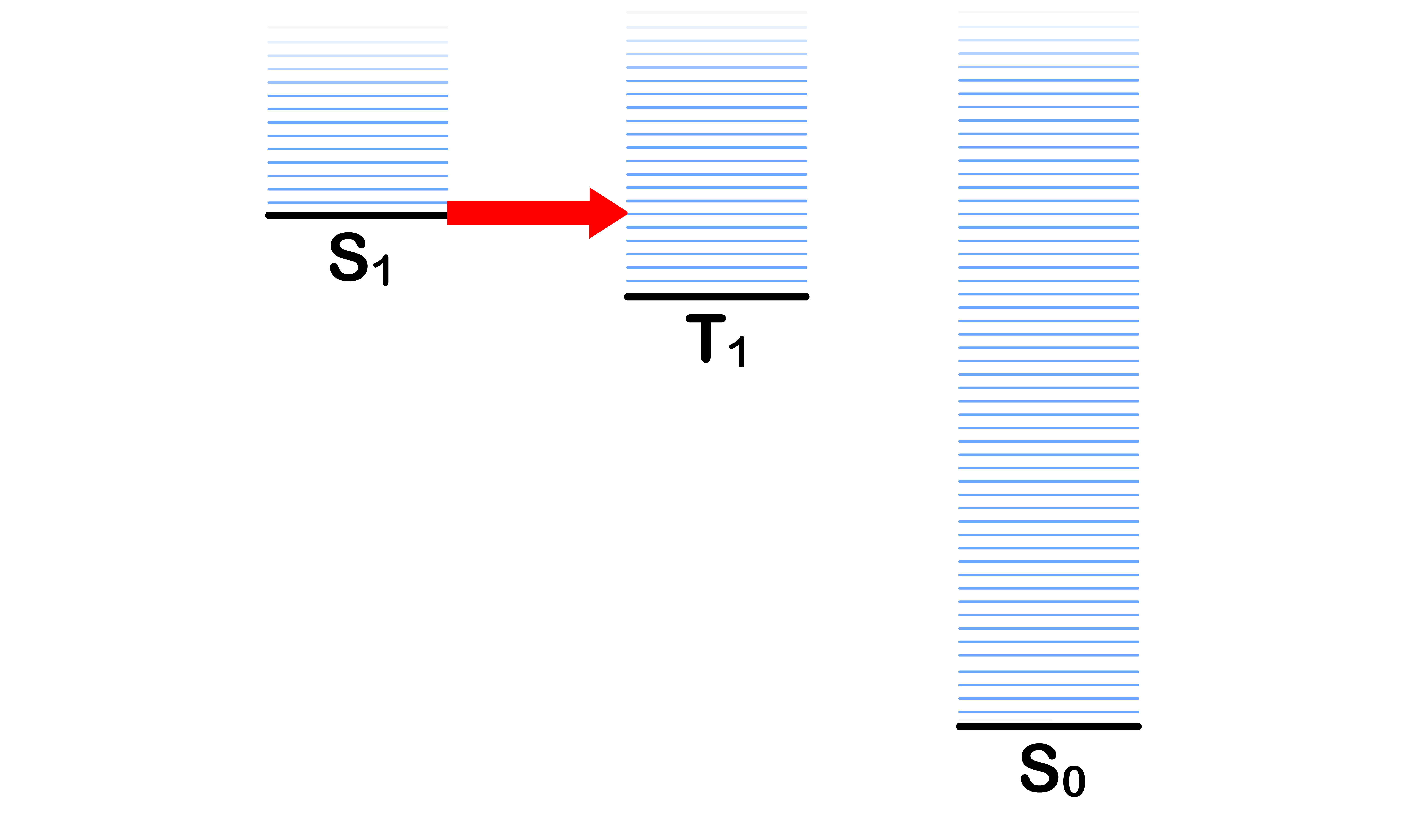
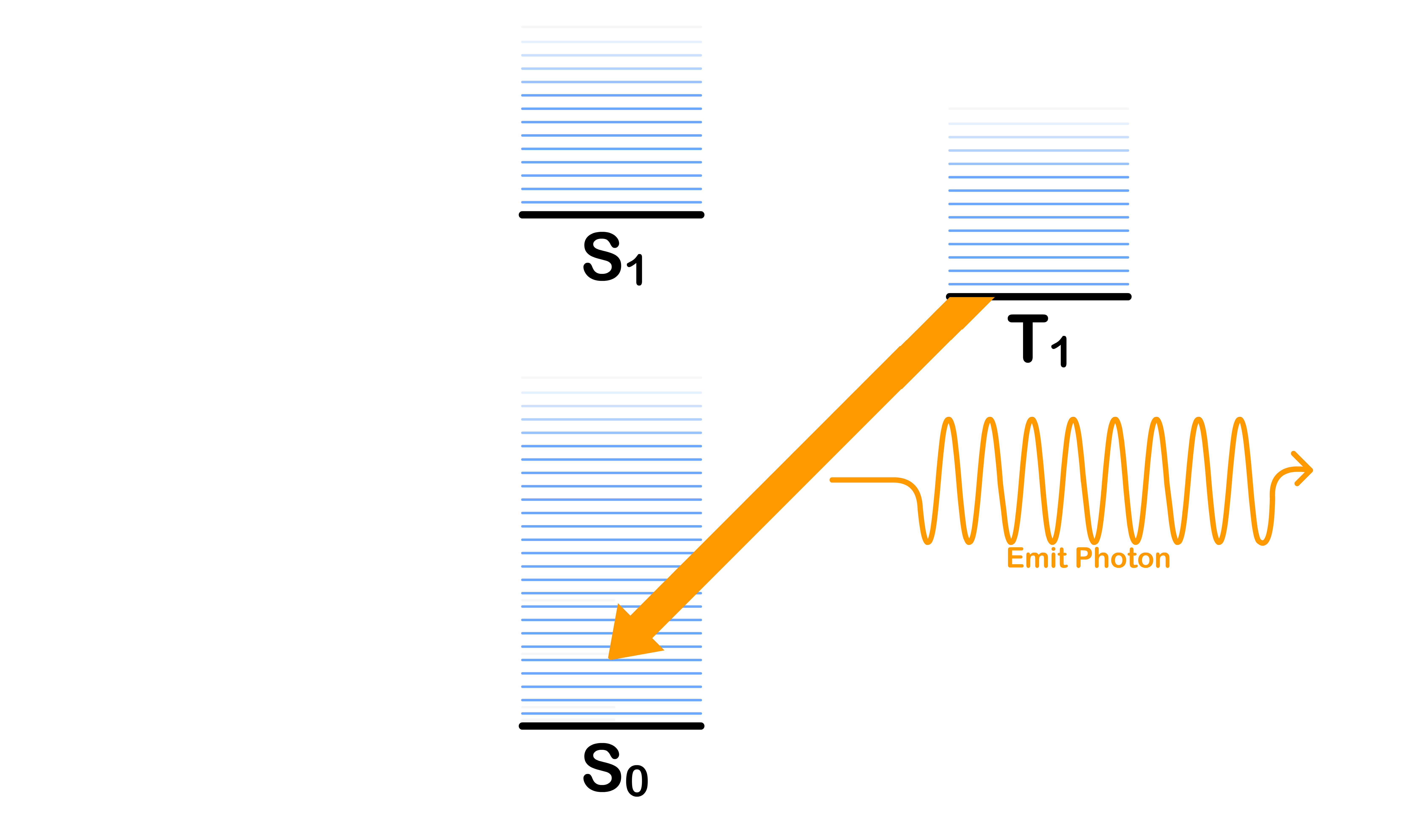
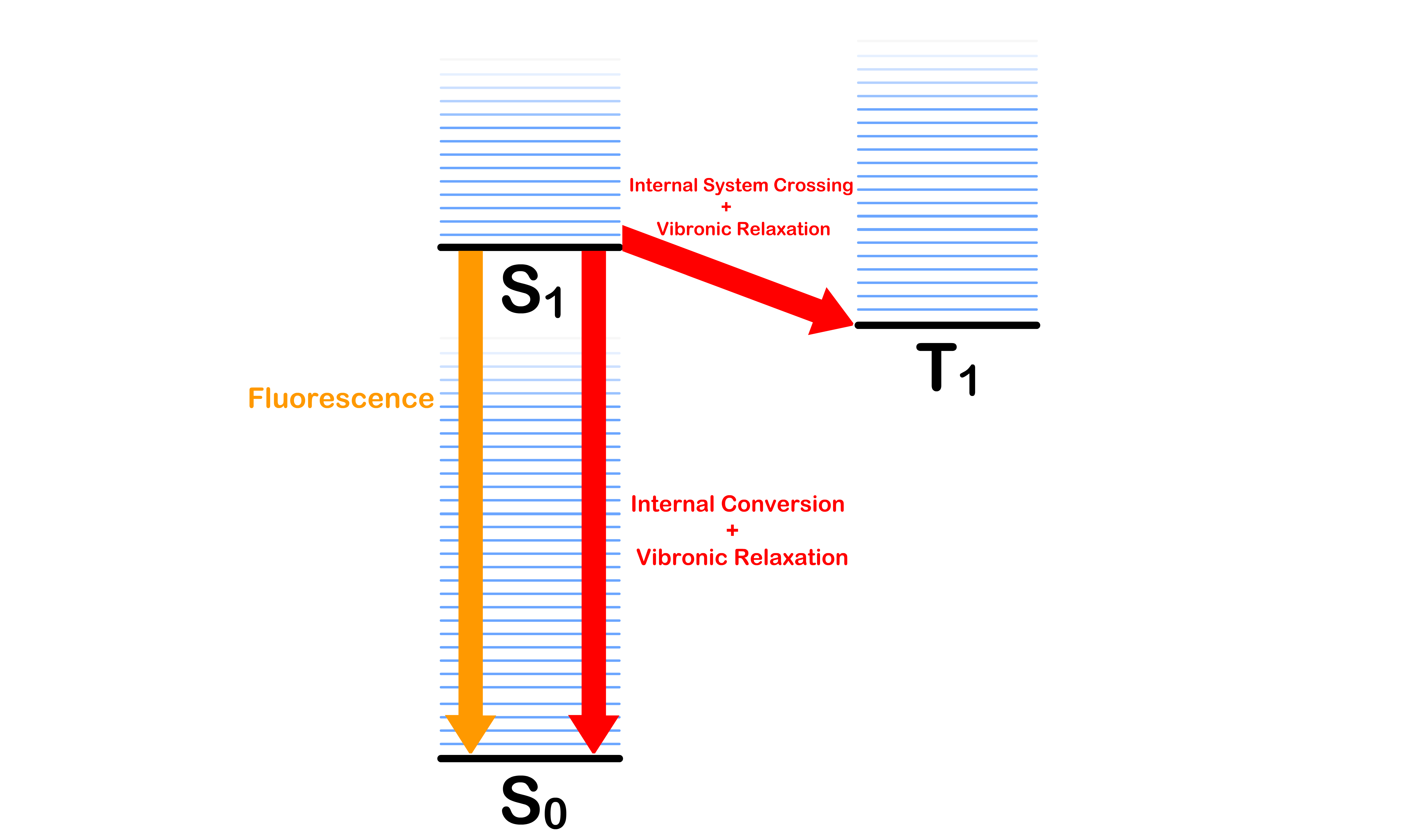
Intersystem Crossing
- Transitioning from the ground vibronic state of to some vibronic state of with a change in spin
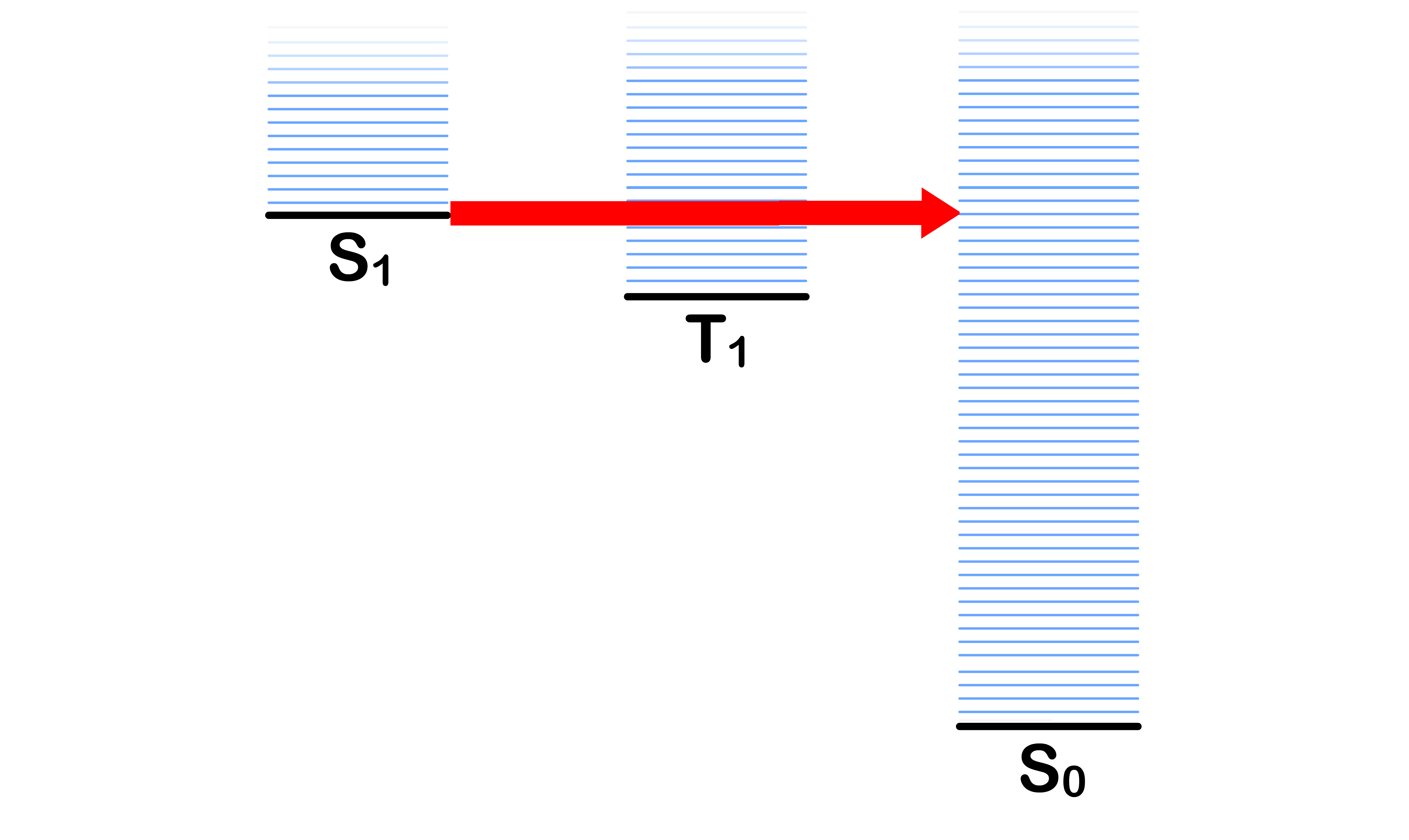
Internal Conversion
- Transitioning from the ground vibronic state of to some vibronic states of without a change in spin
¶ Processes that involve photons
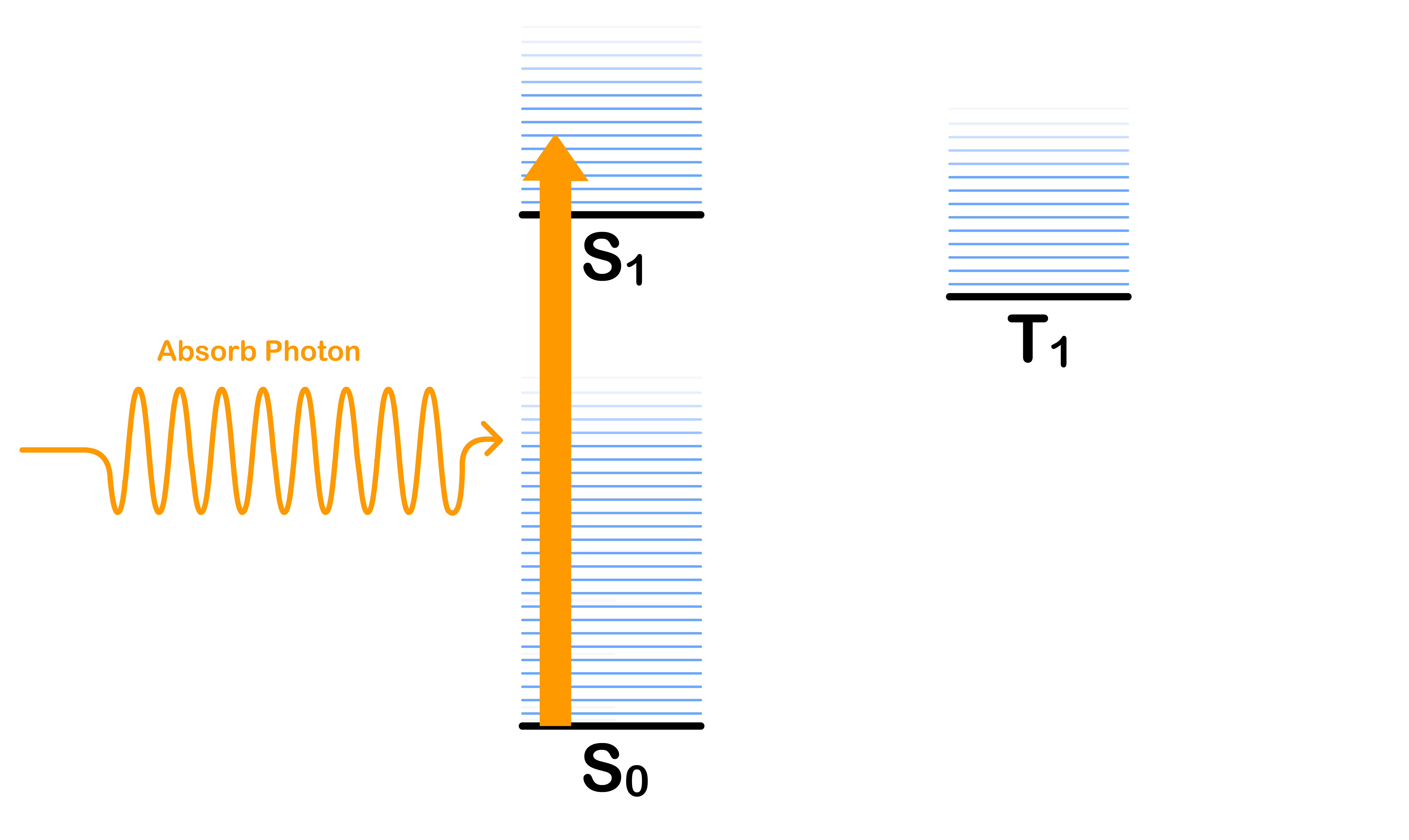
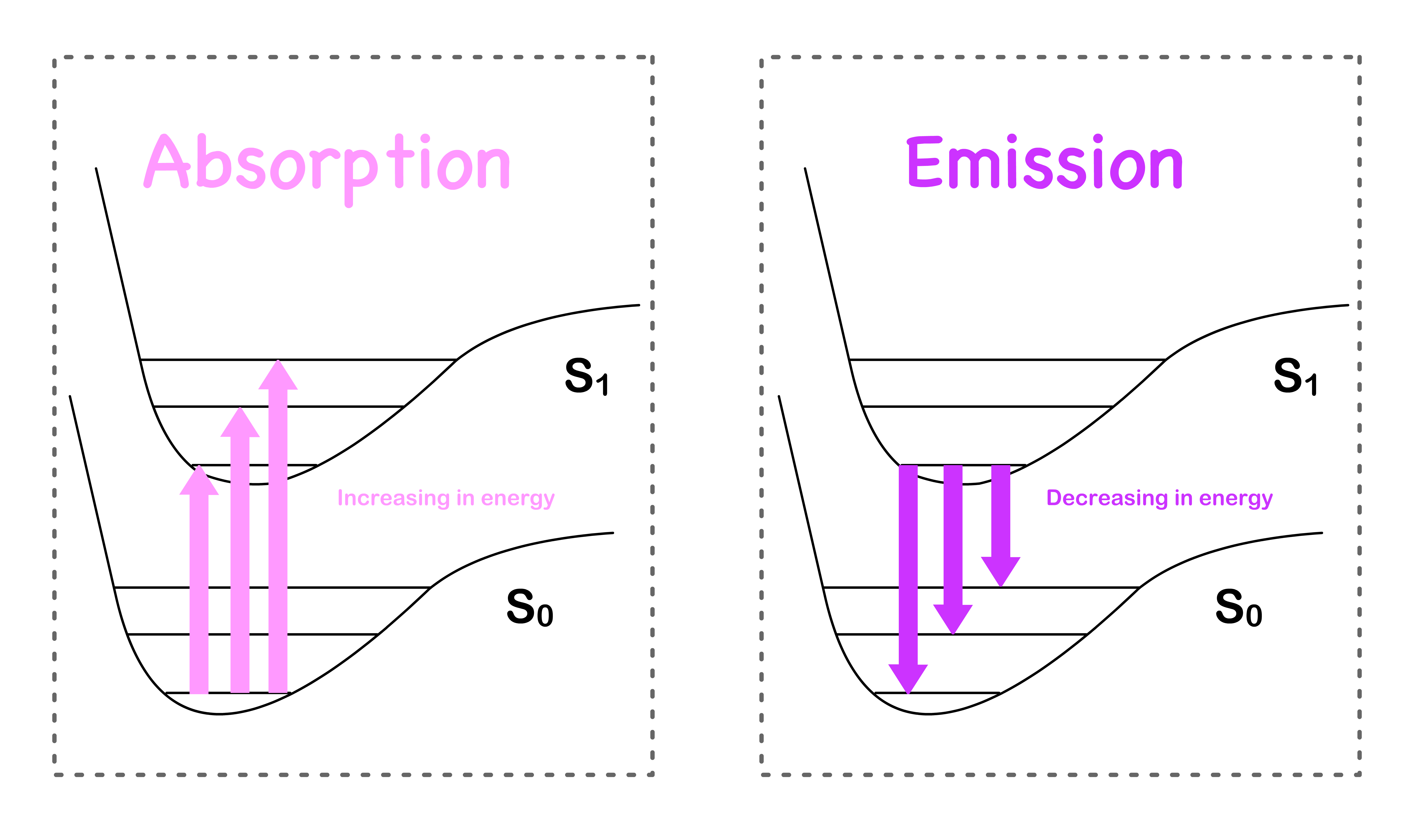
Absorption
- The absorption of a photon excites the molecule from the ground vibronic state of to one of the vibronic states of
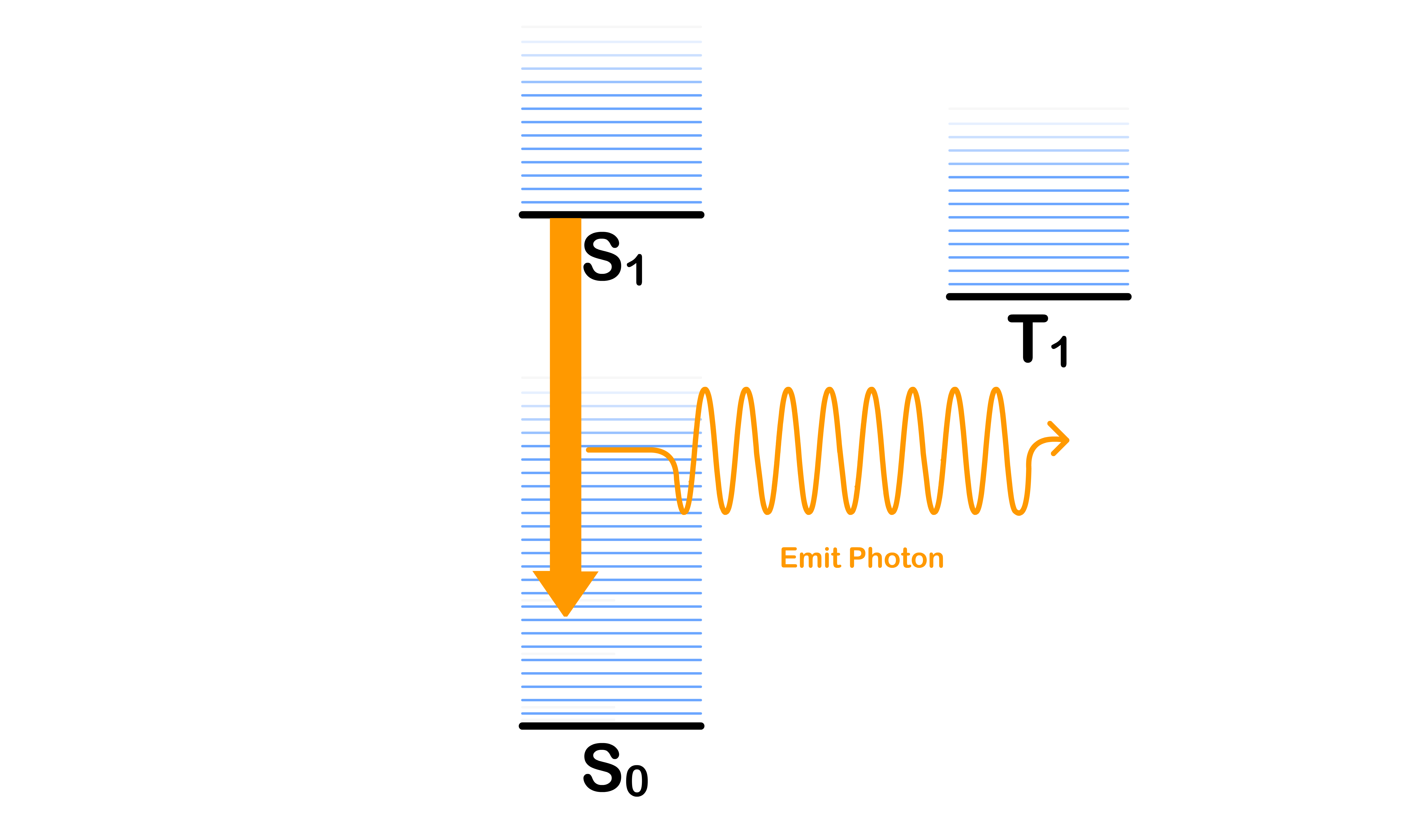
Fluorescence
- The emission of a photon causes the excited molecule decay from the ground vibronic state of to one of the vibronic states of
Phosphorescence
- The emission of a photon causes the excited molecule decay from the ground vibronic state of to one of the vibronic states of
¶ Fermi's Golden Rule
In photochemistry, there are two factors that dictates the rate of processes
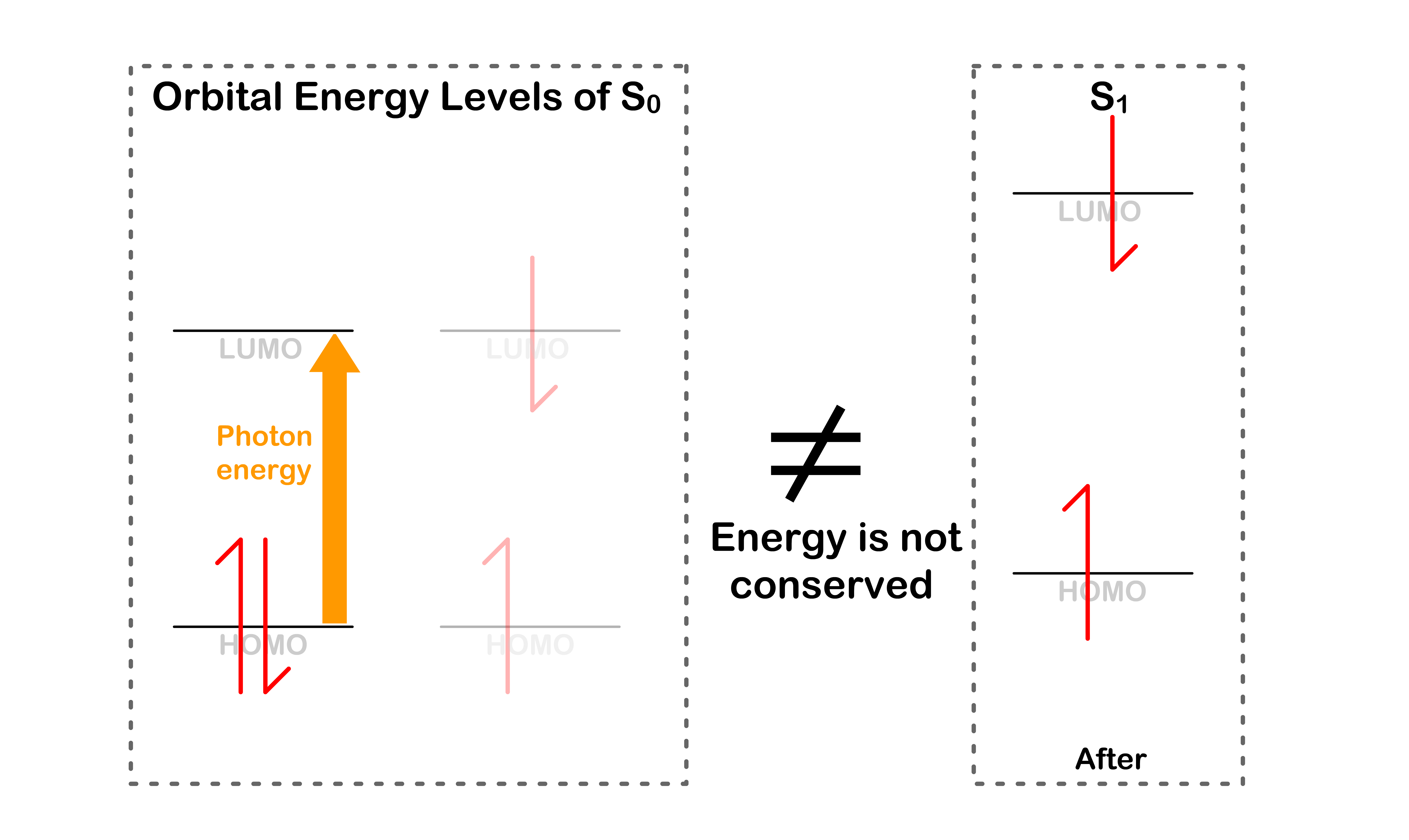
- Energy is conserved during the transition
- The process is favorable given that energy is conserved
In photochemistry, the rate constant of a process is dictated by the Fermi's Golden rule
- is the rate constant of the process ()
- , the Franck-Condon factor tells us how often the process will be in a state where energy is conserved during the transition
- , the tunneling coefficient tells us how favorable the process is given that the requirement for conservation of energy is already fulfilled
¶ Processes that involve Photons
There are three processes that involve photons, absorption, fluorescence and phosphorescence
- They all behave similarly in the eyes of Fermi's Golden Rule
¶ The Franck-Condon Factor ( FC )
- The Franck-Condon Factor is concerned with whether the transition conserves the total energy of the system
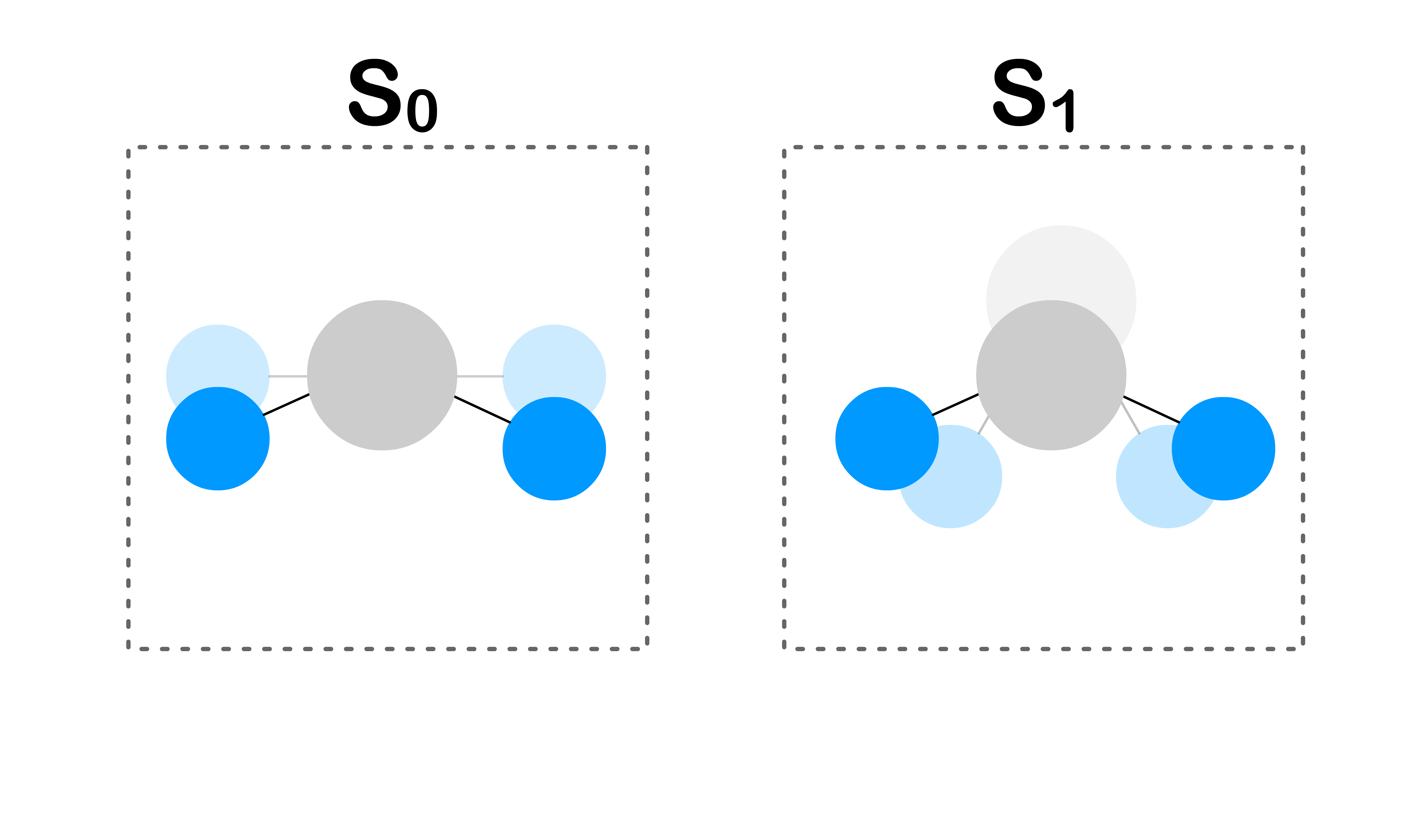
- Different electronic states have different electron configurations, and molecules can adopt different geometries when they have different electron configurations (e.g. different bond length, different shape)
- This change in geometry is due to the change in charge distribution within the molecule
- A different geometry means that the orbital energy levels will be different for different electronic states
- A different orbital energy means that the total energy is not conserved after the transition
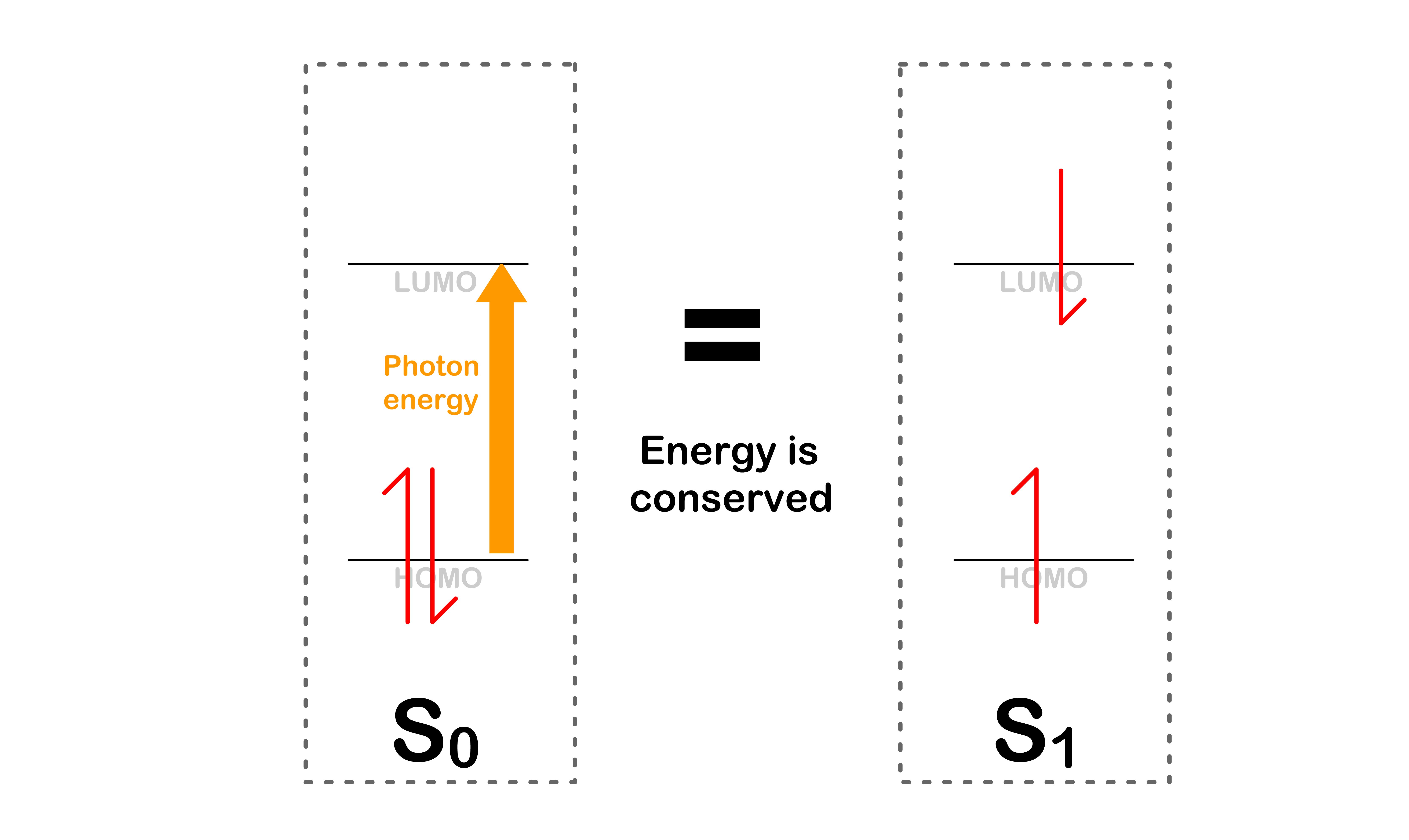
Transition is ONLY allowed when energy is conserved
- This will only happen if the orbital energy levels are the same before and after the transition
- In order for the orbital energies to be the same, the molecule must adopt the same geometry for both electronic states at the moment of transition
- Fortunately, the geometries of both electronic states can change via vibration
- The transition is only allowed when the geometries of the two electronic states are the same
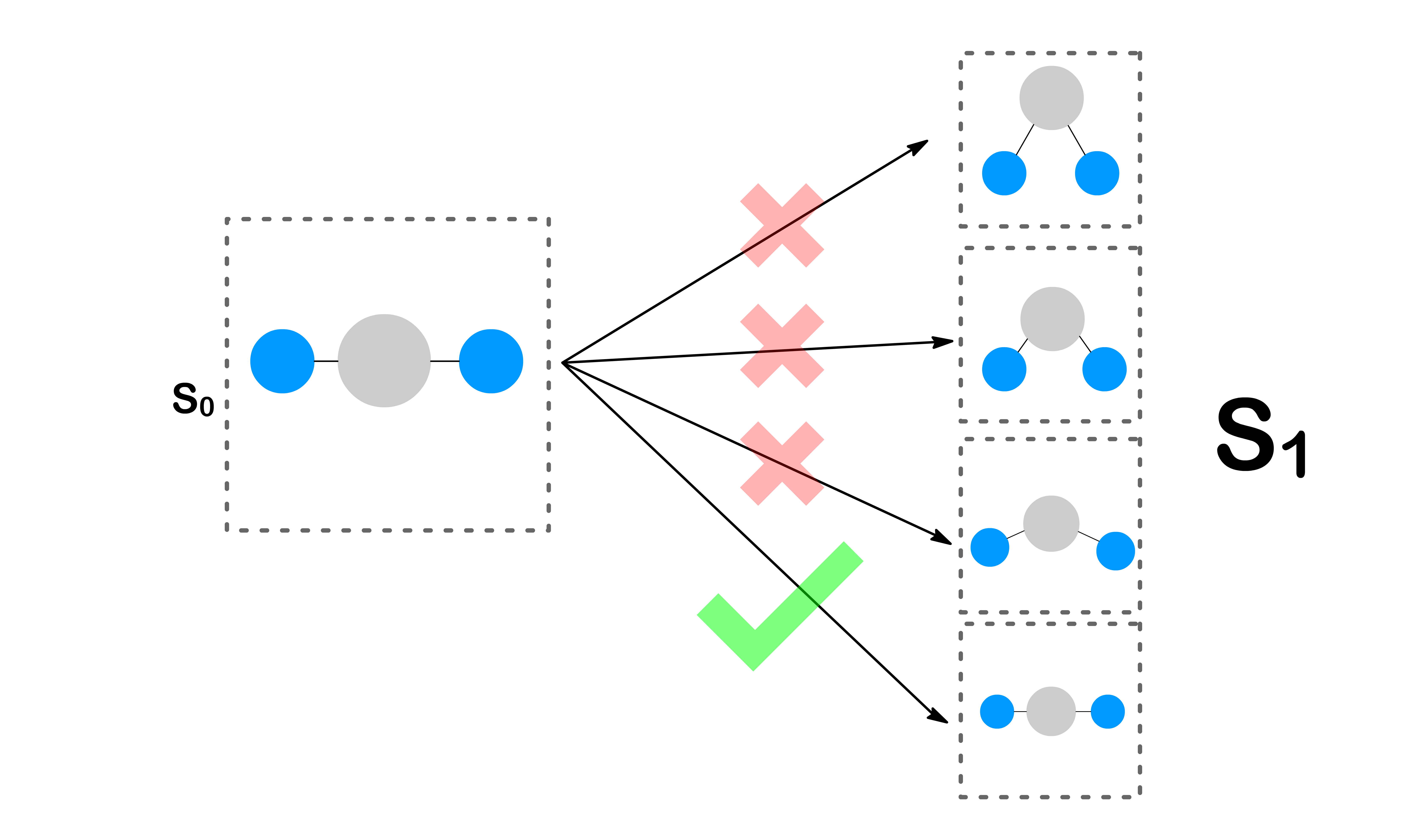
- The more similar the geometries, the easier it is to achieve the same geometries through vibration
- Since the geometry of molecules are defined by the position of the nuclei and the position of the nuclei are defined by the nuclear wavefunctions, the similarity of geometry can be measured by the similarity of the nuclear wavefunctions
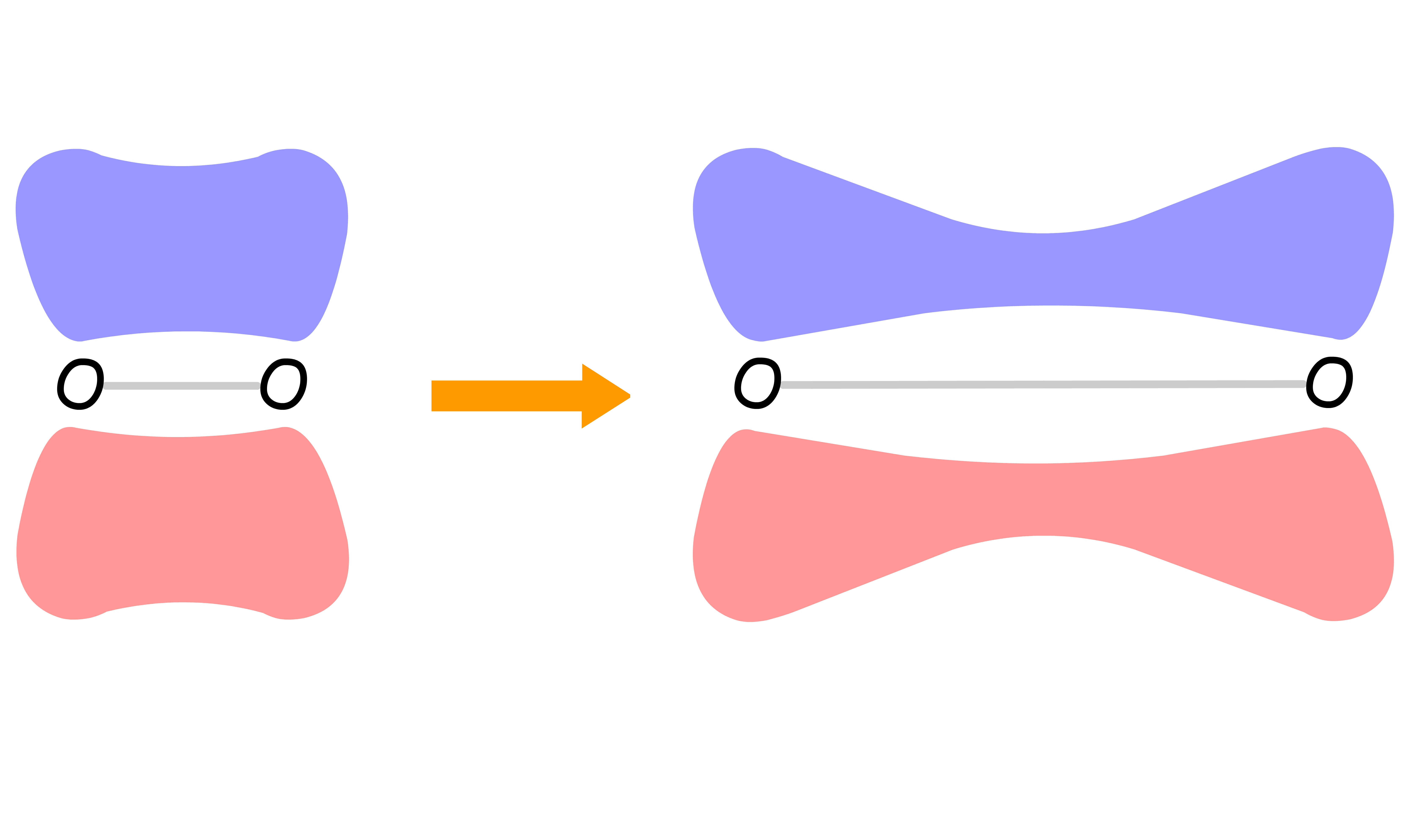
- As established before, we can measure the similarity of functions or vectors by using the inner product
- Hence, the Franck-Condon factor is given by
Nuclear wavefunction = Vibronic Wavefunction
- The nuclear wavefunction is the same thing as the vibcronic wavefunction since vibration is nothing but the constant changing in position of the nuclei
- Hence, the greater the overlap of the vibronic wavefunctions, the larger the Franck-Condon Factor
The Franck-Condon Factor is different for different vibronic transition
- In general, as we shift the potential energy surface of the state from left to right, the greatest overlap between vibronic wavefunctions will shift from
Assumption behind Franck-Condon Principle :
- Because nuclei are so much massive than electrons, an electronic transition takes place very much faster than the nuclei can respond
- On the timescale of electronic reorganisation, going from one electronic state to another, the nuclei will appear frozen – they will respond, but much more slowly.
- We assume initially that the nuclei are frozen and light absorption therefore corresponds to a vertical transition between potential energy surfaces
¶ The Tunneling Coefficient ( V2 )
- The Tunneling Coefficient is concerned with whether the transition is favorable if the requirement for conservesation of energy is met
An appeal for intuition (not a proper derivation)
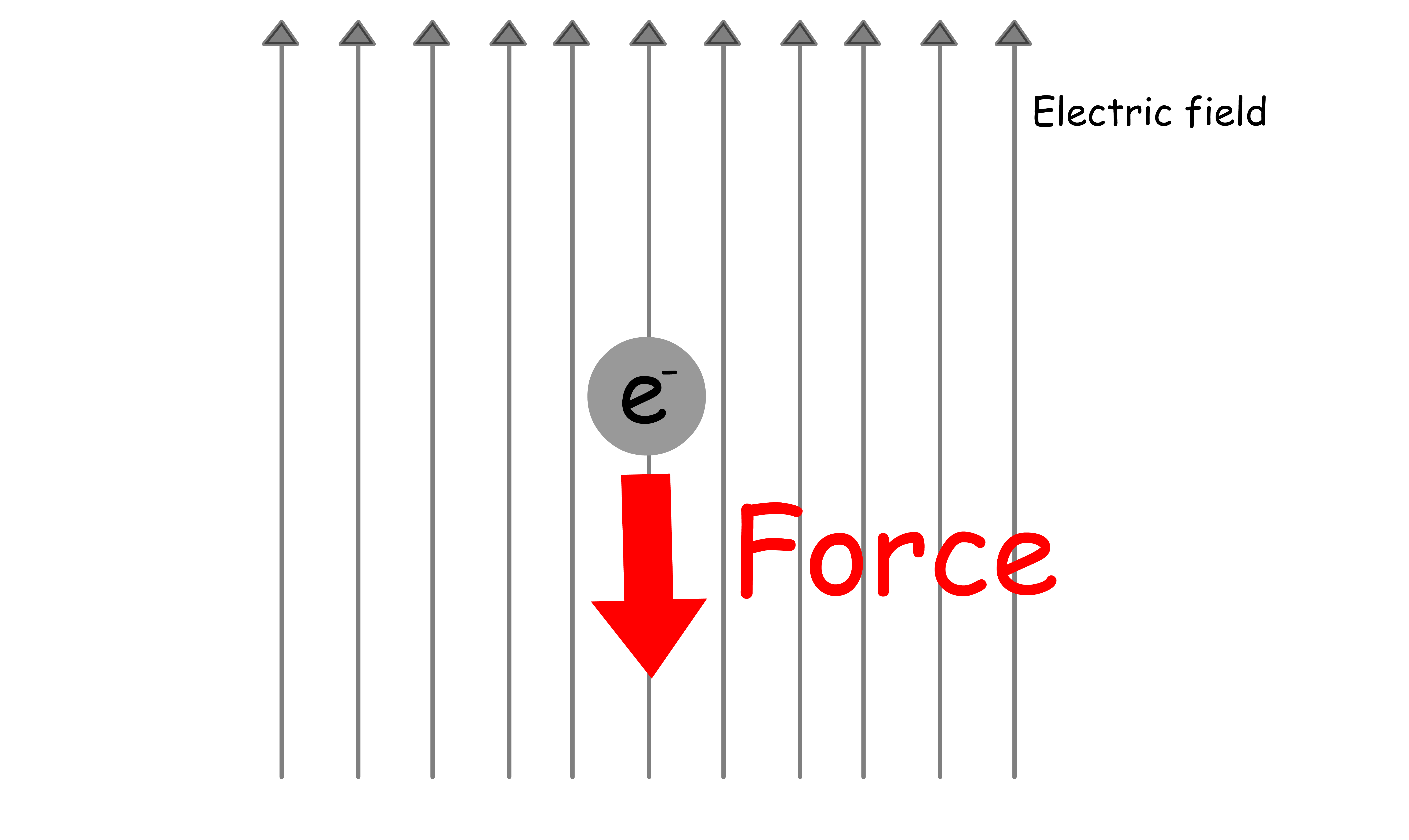
- Electrons are charged particles, so they will experience forces under electric field
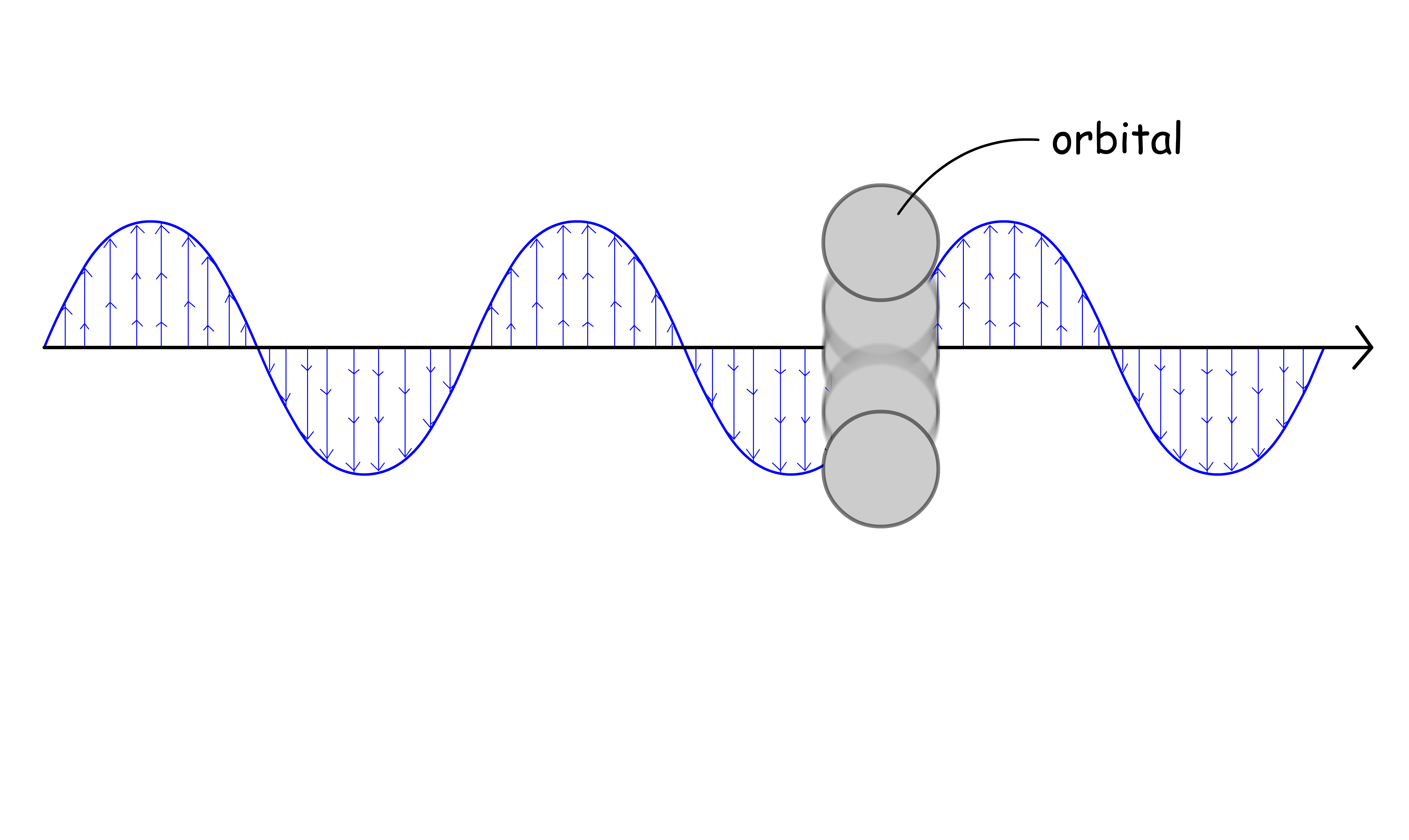
- Classically, light can be treated as oscillating electric field. Hence, orbitals, which is basically just electrons, will oscillate back and forth under the influence of light
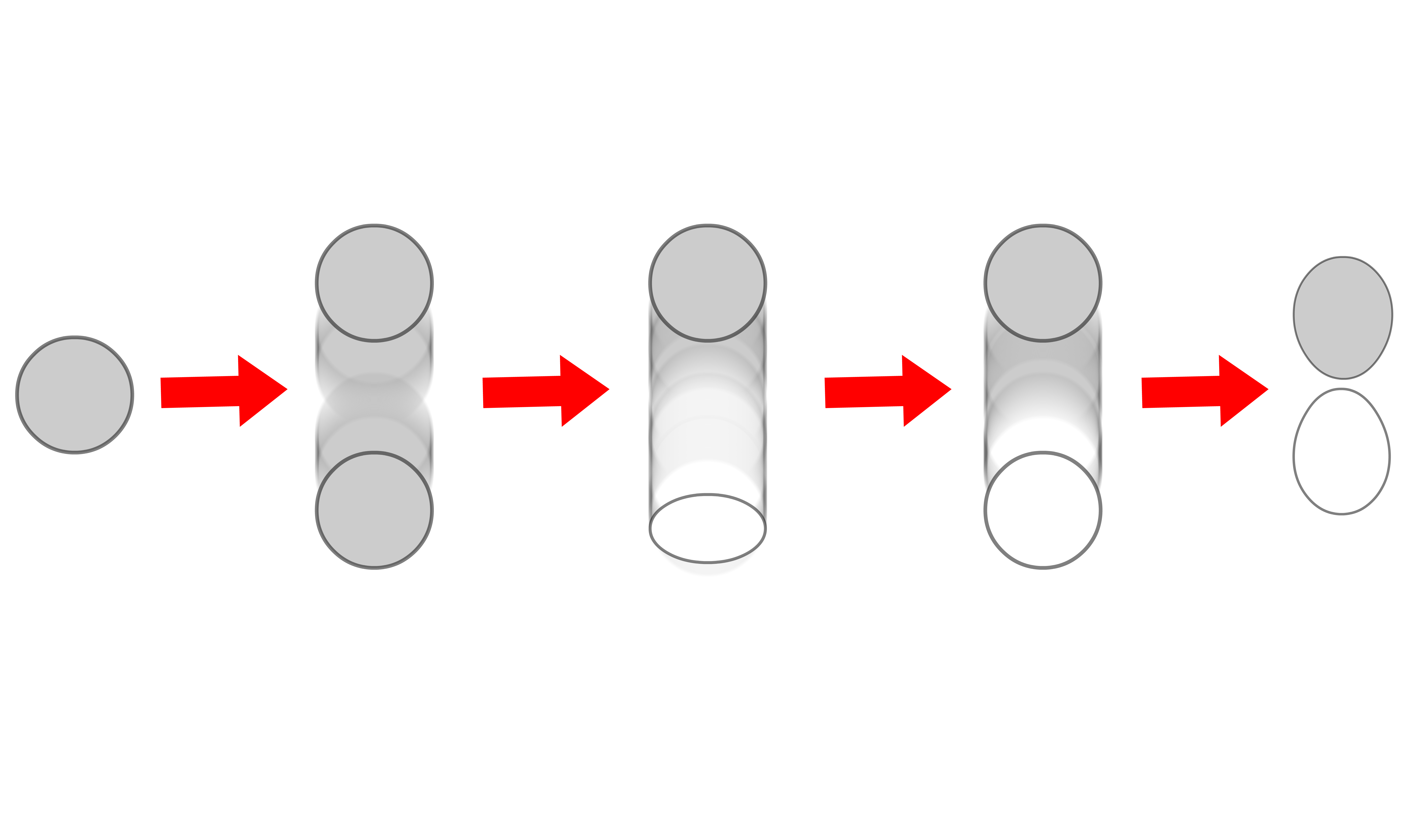
- Overtime, the oscillating orbital (HOMO) will be "transformed" into a new orbital
- Intuitively, we would think that the electron will transition to an orbital (usually the LUMO) that resembles the "transformed HOMO"
- We can therefore tentatively conclude that how favorable the transition is given by the similarity between the actual LUMO and the "transformed orbital"
- Mathematically, the measure of similarity can be achieved with inner products, so V is given by
- The "transformed orbital" is generated by operating the HOMO with the electric field
- The tunneling coefficient can therefore be expressed as such
Transition Dipole
- Focusing on the ability of the molecule to respond to the light field, we define a term called the Transition Dipole ()
-The transition dipole is directly proportional to the tunneling coefficient
- Hence, the transition is forbidden when the transition dipole is equal to zero
- The mathematical expression of the transition dipole is given as such, where the electric field ( ) is omitted due to the fact that it is largely constant
- Since the electronic wavefunction can be expressed as a product of the spatial wavefunction and spin wavefunction, we can expressed the transition dipole as such
- We can therefore see that the transition dipole will be zero if either or is zero
Requirements for Spatial Wavefunctions
Transition is only possible if:
- We can express the inner product as an integral
- Since integrating antisymmetric functions will always give you zero in order to make the integral non-zero, we must ensure that is not antisymmetric
- A general rule of thumb is that multiplying symmetric or antisymmetric functions are like multiplying +1 and -1
- We know that is an antisymmetric function, so the product of the two spatial wavefunctions must be antisymmetric in order for the whole thing to be symmetric
- In order for the product of the wavefunctions to be antisymmetric, the initial and final wavefunction must be of different symmetry (different symmetry label / different irreducible representation)
Requirements for Spin Wavefunctions
- The inner product of spin wavefunctions are given as such
- When the spin state is different after the transition, the inner product is zero
- Hence, a change in spin during the transition is forbidden
- However, we haven't accounted for spin-orbit coupling. If the effect of spin-orbit coupling is significant, then transitions with a change of spin will be allowed, albeit slow
- The effect of spin-orbit coupling is directly proportional to the charge of the nucleus raised to the 4th power
¶ Processes that don't involve Photons
There are three processes that don't involve photons, vibronic relaxation, intersystem crossing and internal conversion
- They all behave similarly in the eyes of Fermi's Golden Rule
¶ The Franck-Condon Factor ( FC )
- The Franck-Condon Factor is concerned with whether the transition conserves the total energy of the system
- In order to conserve energy, the initial and final state must be isoenergetic at the moment of transition:
- Although the energy levels between the initial and final state may not be identical, the vibration of molecule will cause fluctuations of energy levels and bring the two states to the same energy level
- If the initial final state are close in energy to begin with, it will be a lot easier for them achieve isoenergeticity
- Hence, the Franck-Condon Factor is inversely proportional to the energy gap between the initial and final state
- In general, the Franck-Condon Factor is enhanced by lots of vibrations (large, floppy molecules) and small energy gap
¶ The Tunneling Coefficient ( V2 )
The Tunneling Coefficient is concerned with whether the transition is favorable if the requirement for conservesation of energy is met
It turns out both internal conversion and intersystem crossing violates the Born-Oppenheimer Approximation
In essence, the Born-Oppenheimer Approximation states that the molecular wavefunction can be written as a product of the nuclear wavefunction, the spatial orbital wavefunction and the spin wavefunction
- Our assumption so far is that each of these wavefunctions only depend on their corresponding independent variable and that each wavefunctions do not depend on each other
- It turns out that this assumption breaks down when we discuss internal conversion and intersystem crossing
Internal Conversion
- The nuclear wavefunction couples to the spatial orbital wavefunction
- This will be apparent if we consider a situation where we slowly increases the internuclear distance and see how the molecular orbitals respond to that change
- We can see that the vibronic wavefunction "mixes in" with the molecular orbital (spatial electronic wavefunction)
- Just like before, the tunneling coefficient is given by how similar the initial electronic wavefunciton is to the final electronic wavefunction
- Due to the additional mixing of vibronic wavefunction to the electronic wavefunction, we can say that the magnitude of the term is given by the coupling of Molecular Orbital to vibrations (vibration specific)
Intersystem Crossing
- The spin wavefunction couples to the spatial orbital wavefunction
- The orbital angular momentum mixes with the spin angular momentum and result in a phenomenon called spin-orbit coupling (learn more about its derivation here)
- A change of spin is forbbiden in the absence of spin-orbit coupling (check transition dipole)
- Hence, the more significant the effect of spin-orbit coupling, the more likely the spin can change
- The strength of spin-orbit coupling is dictated by the nuclear charge
- Intersystem crossing is normally slow compared to equivalent IC Greatly enhanced with heavy atoms
¶ Spectrums
¶ Oscillator strengths
- The Beer-Lambert law is used to experimentally measure and quantify light absorption
- We quantify the strength of absorption at a particular wavelength by using the concept of an extinction coefficient
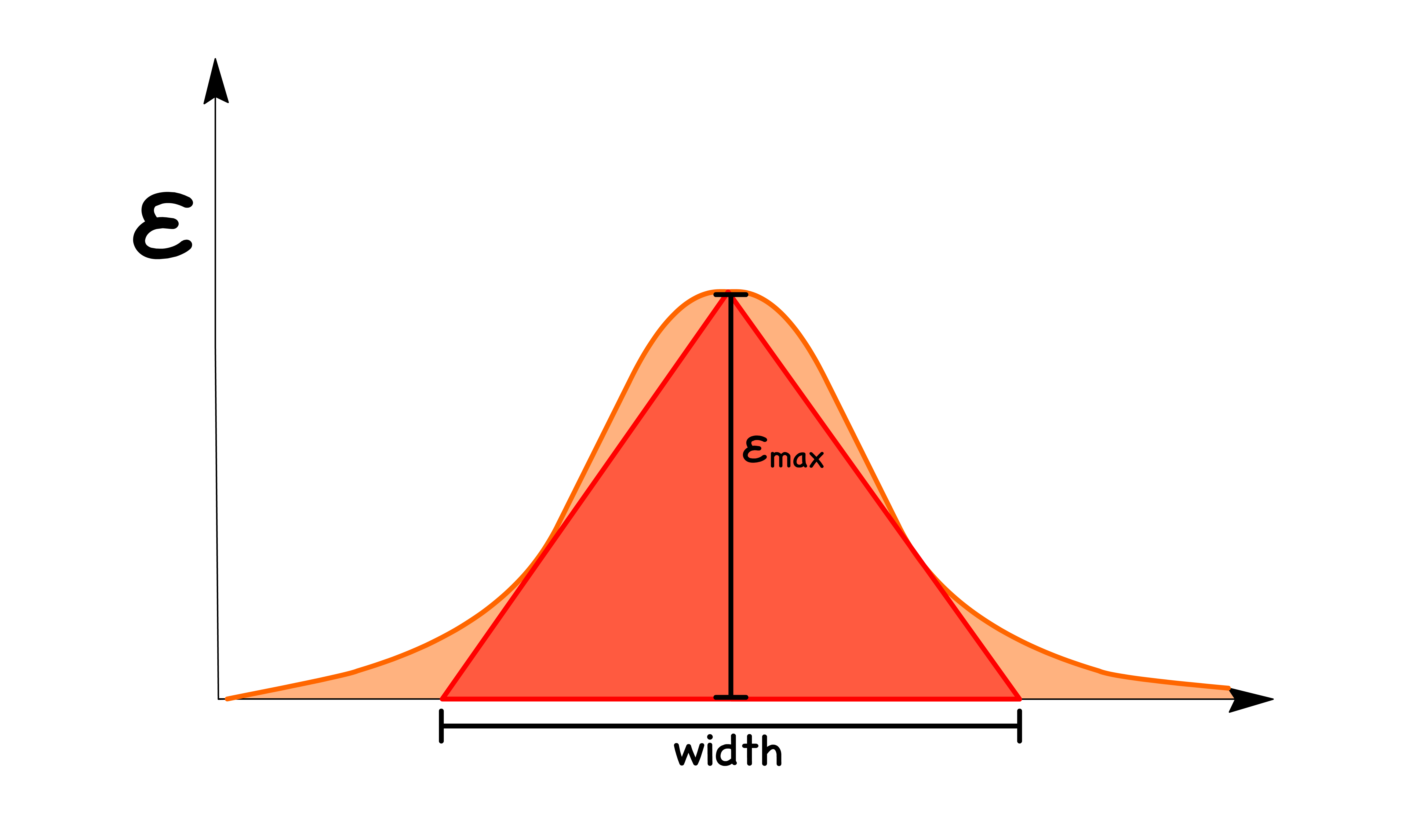
- A good parameter for the strength of absorption is the area under the peak and we call this parameter the oscillator strength ( )
- The term can be thought of as a normalization factor such that the strongest peak will have an oscillator of 1
- Computing integrals is usually a pain in the ass, so we can resort to approximation. Since most peaks have a Gaussian-ish shape, and so we can approximate the area undrneath it using an a triangle
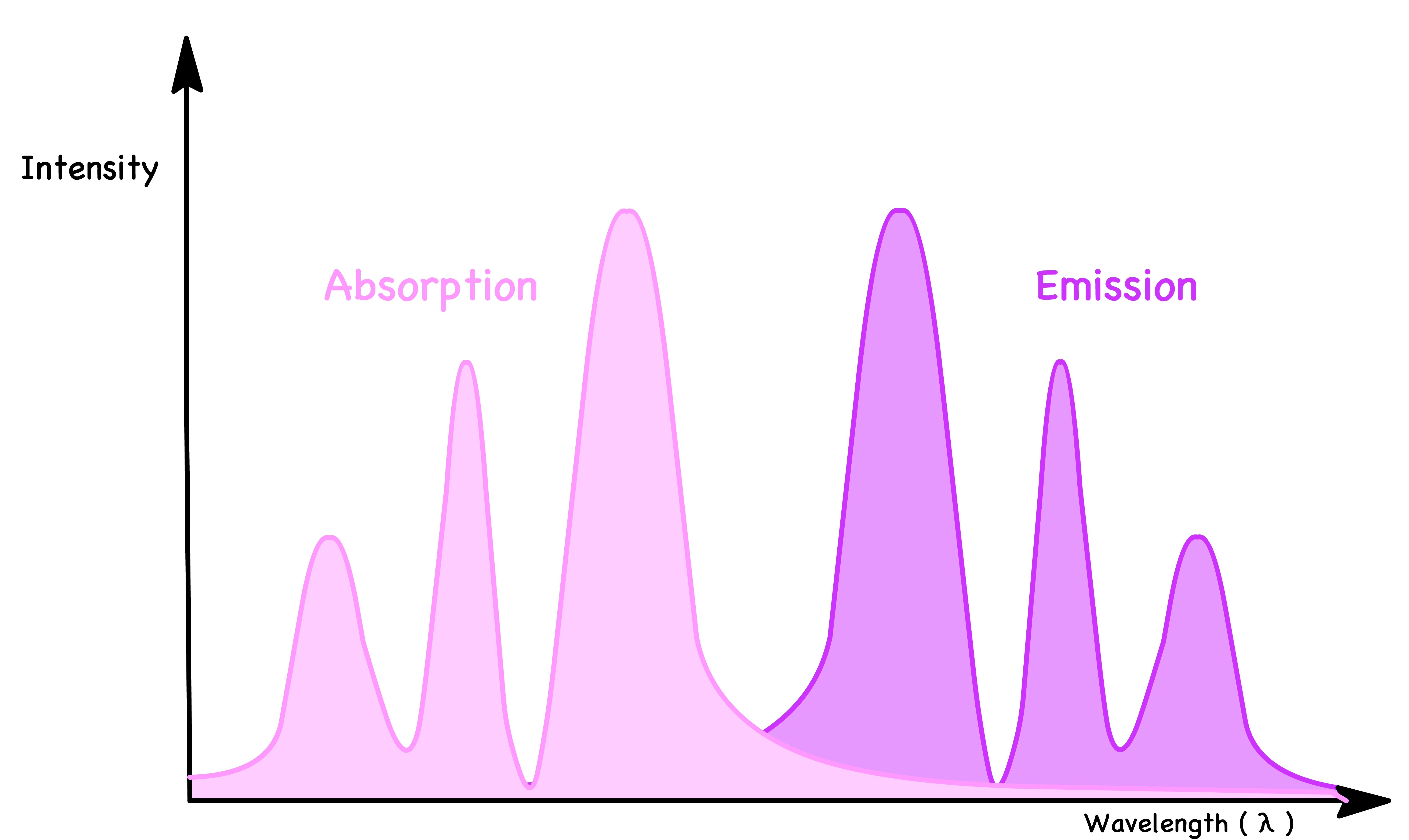
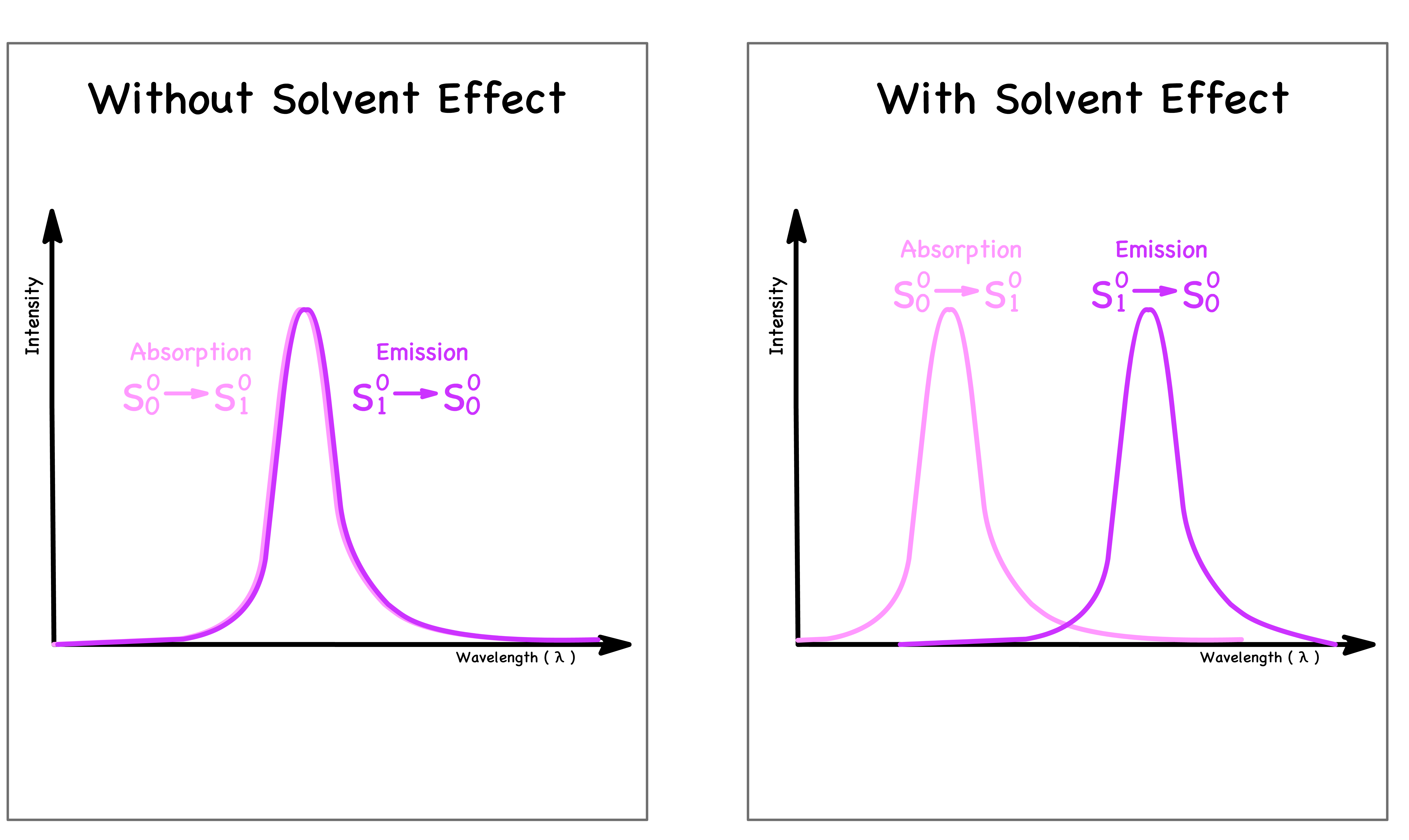
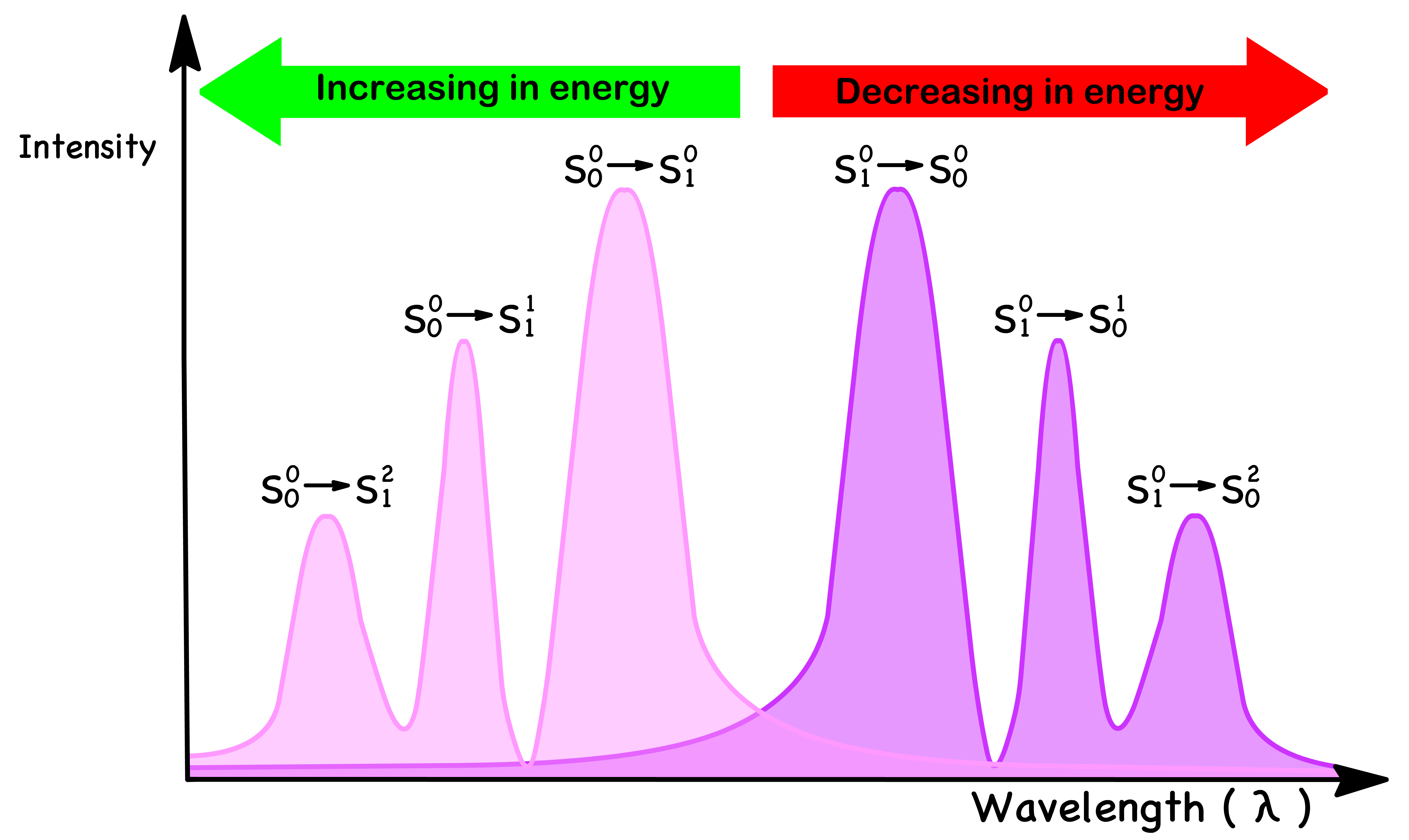
¶ Absorption Spectrum and Emission Spectrum as Mirror Images
- To understand why the absorption and emission spectrum has these kind of relationships, we need to break down the situation into a few different questions
- Why is the absorption transition peak not perfectly overlapping with the emission transition peak ?
- Why are the photons absorbed are higher in energy than the photons emitted ?
- Why are the relative sizes of the peaks in each spectrum mirroring each other ?
Why is the absorption transition peak not perfectly aligned with the emission transition peak ?
- If we are using the potential energy surfaces to predict the energy of the transition and the transition , we would assume these two transitions will have the same energy
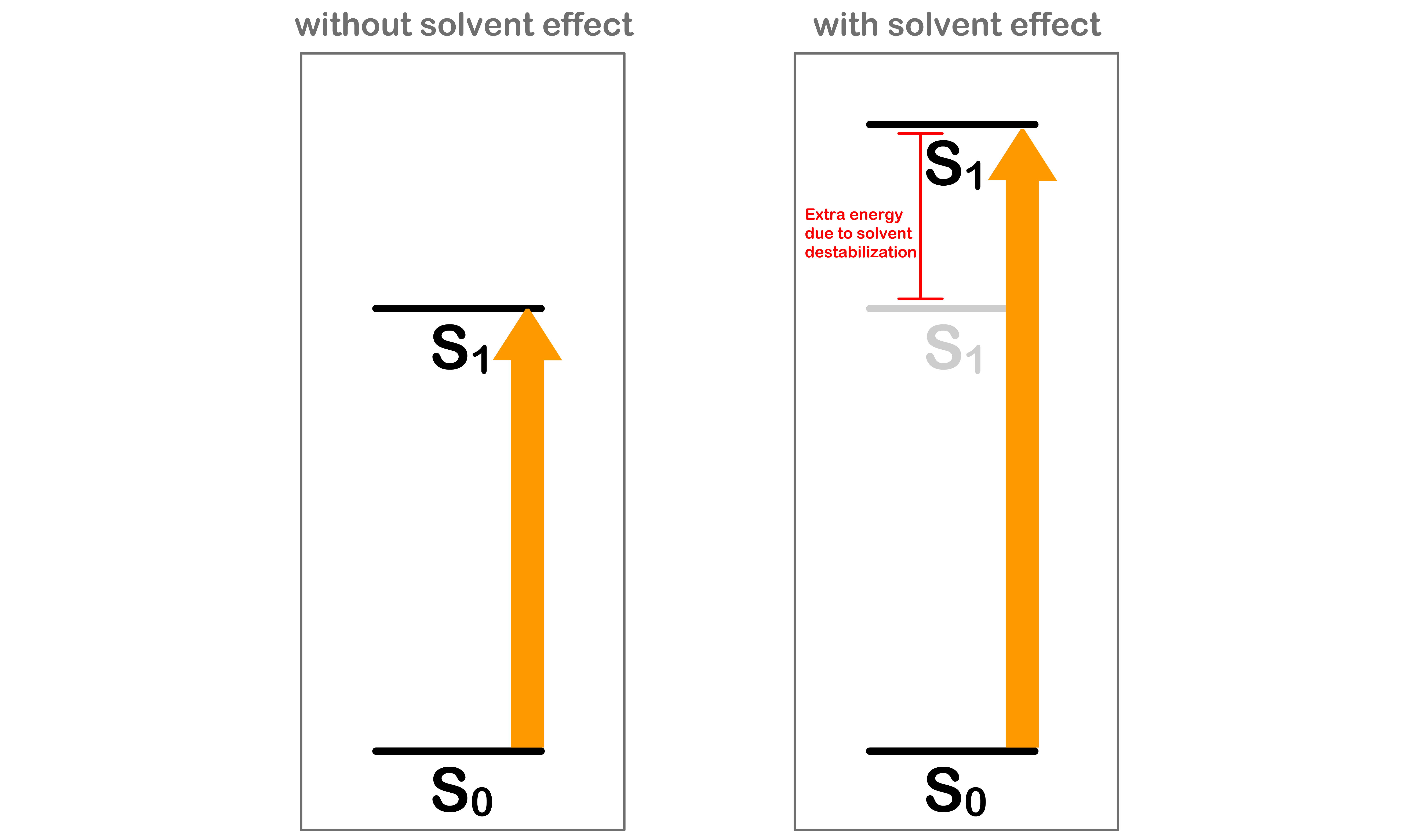
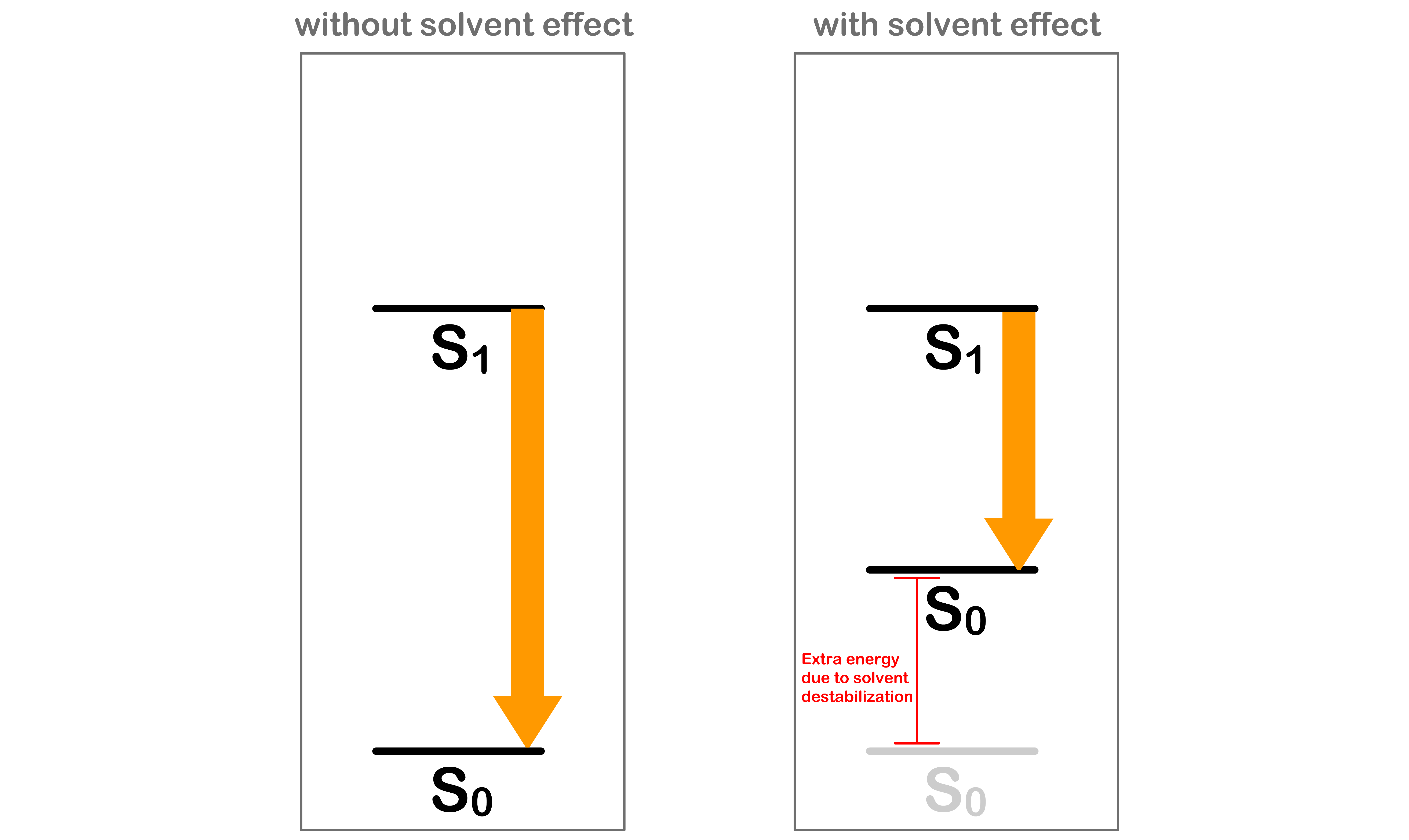
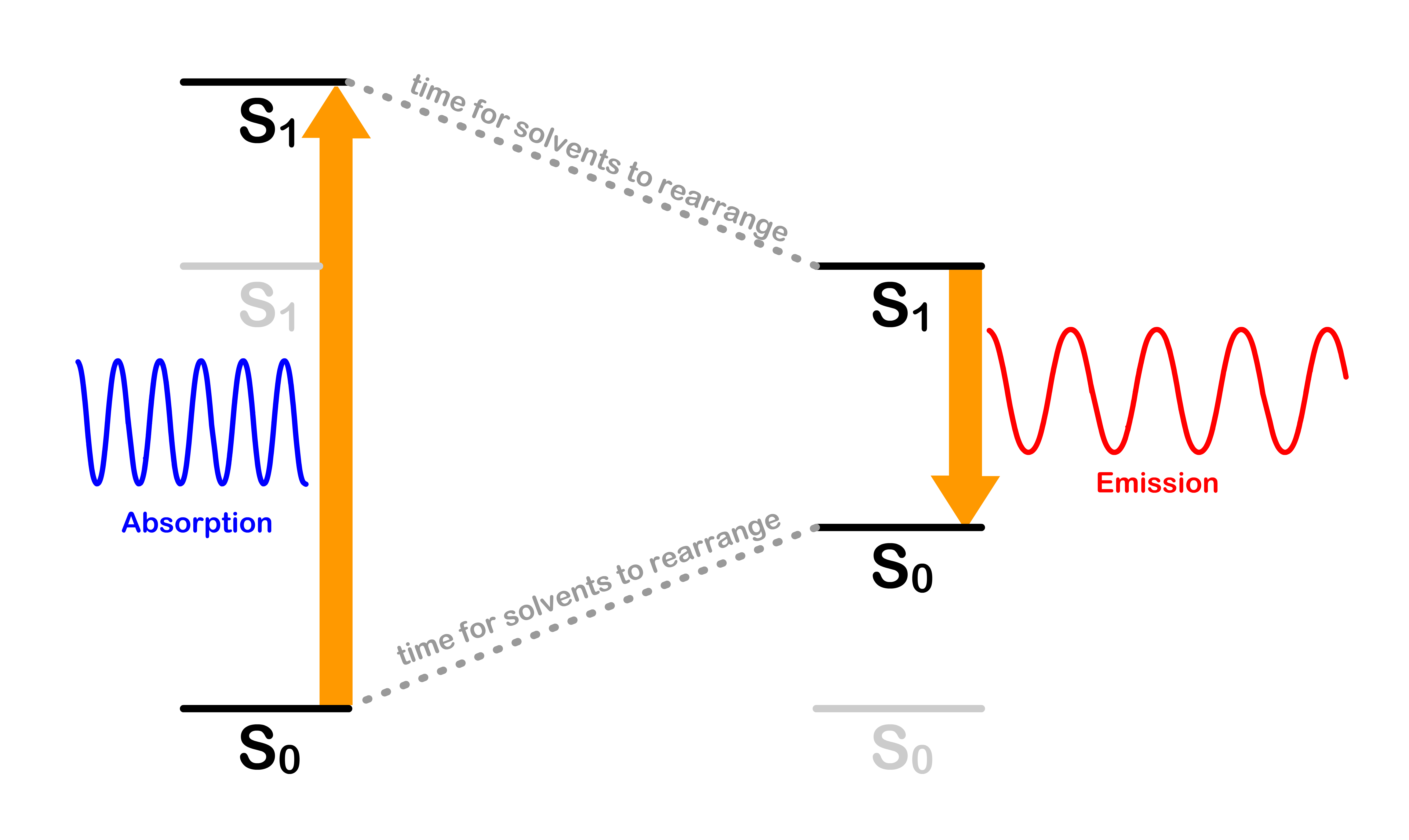
- It turns out that we should also account for the effect of the solvent
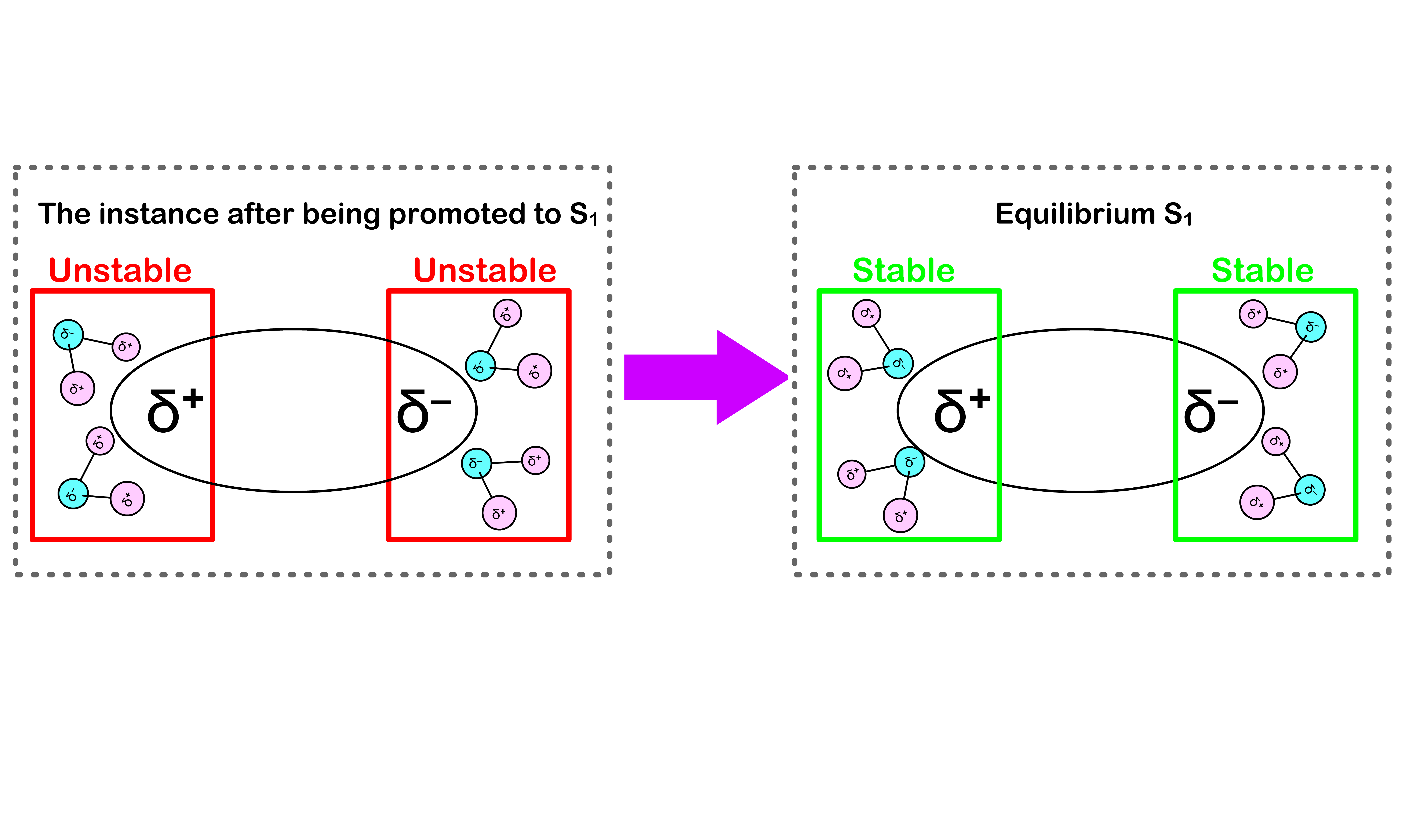
- In equilibrium, the solvents that surrounds the molecule are oriented in a way to achieve the lowest possible energy
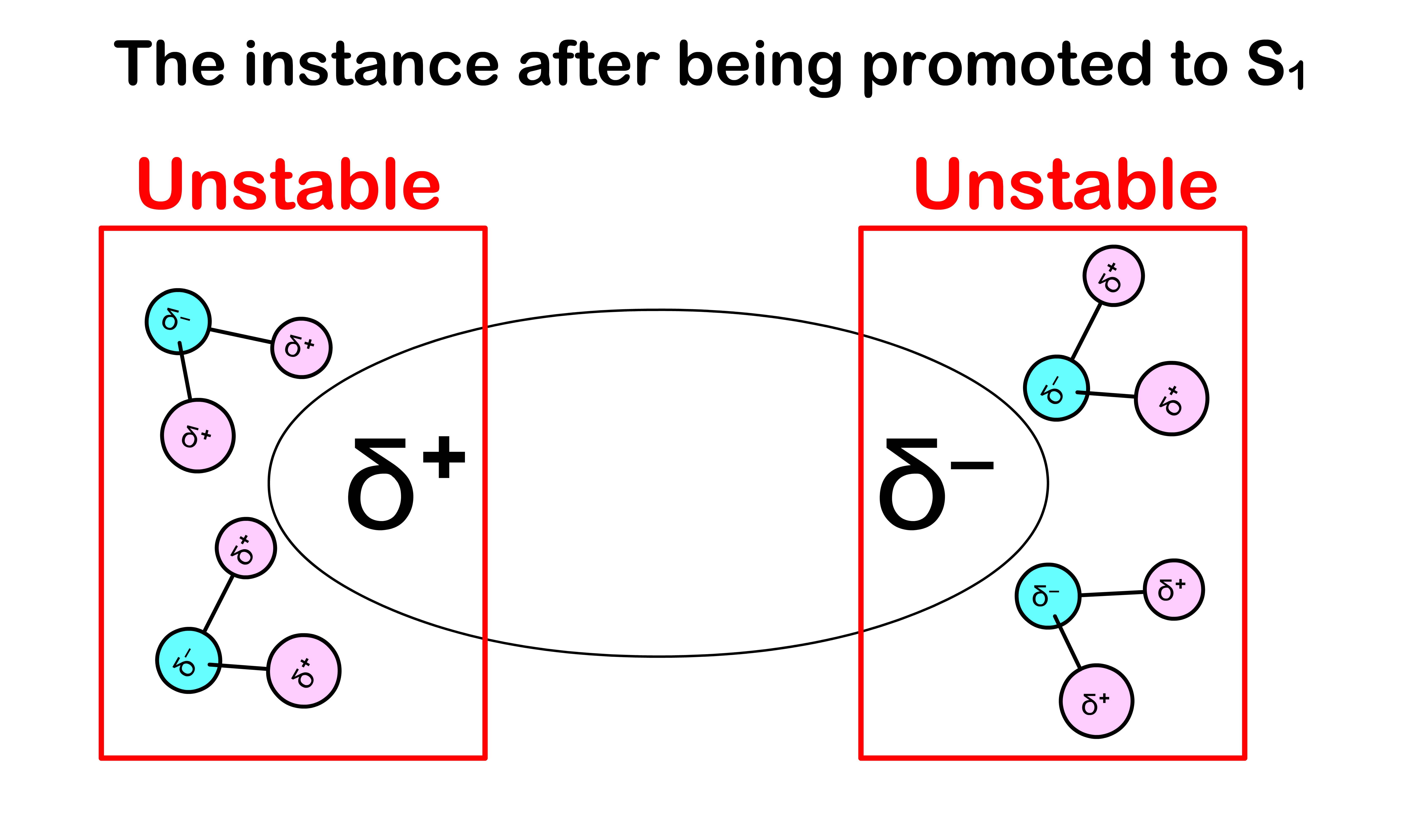
Absorption requires more energy than expected
- Before the absorption, the solvent molecules are oriented in a way that stabilizes the system
- After being excited to the state, the electron configuration of the molecule will be different, which causes the charge distribution within the molecule to change
- Since the absorption is instantaneous, the solvent molecules do not have enough time to re-orient themselves to a stable configuration
- This means that we need extra energy to promote the molecule from to
- Hence, in practice, absorption requires more energy than expected
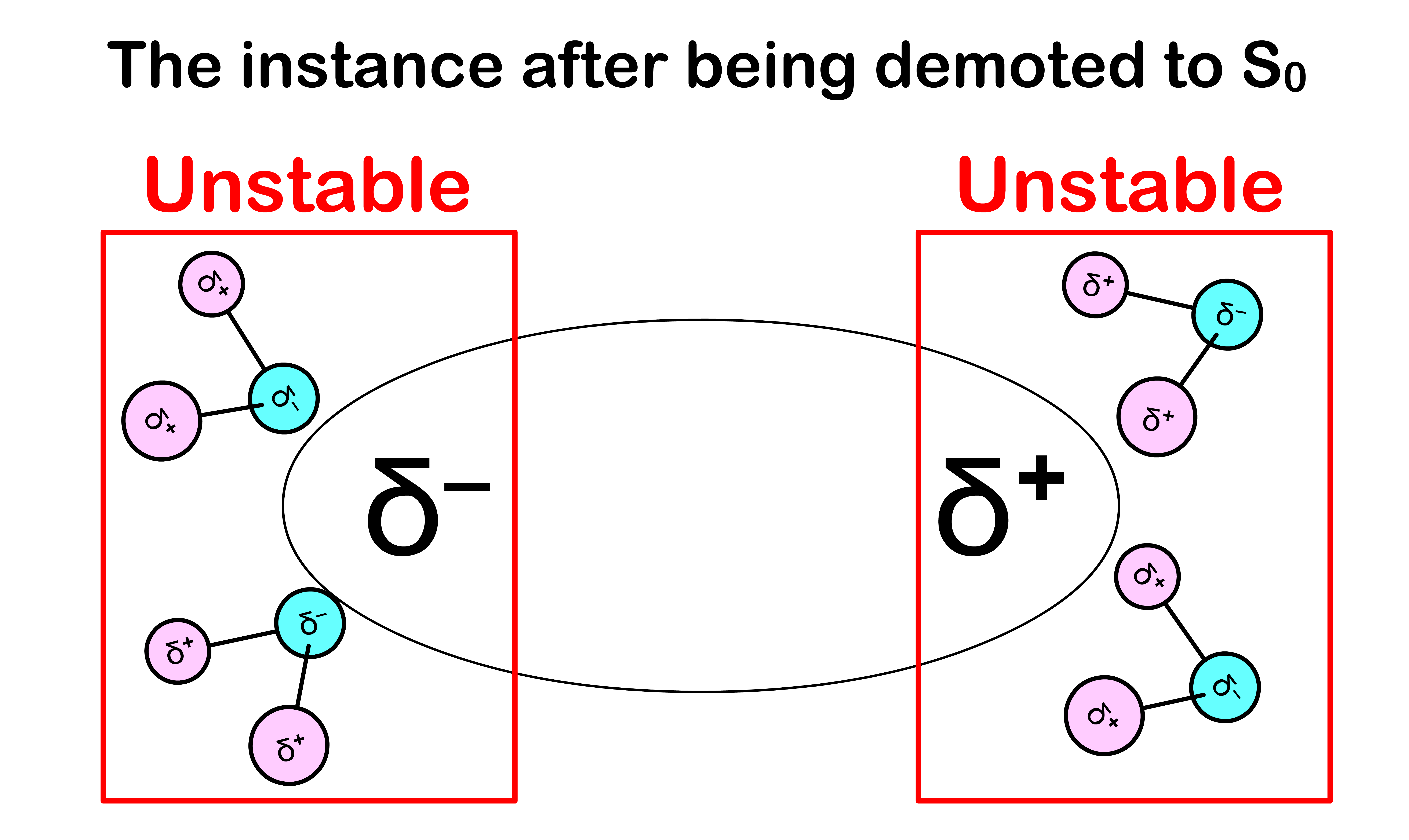
Emission gives out less energy than expected
- After the absorption and before the emission, the solvent molecules have enough time to re-orient themselves to stabilize the molecule in the state
- After decaying back to the state, the electron configuration of the molecule will be different, which causes the charge distribution within the molecule to change
- Since the absorption is instantaneous, the solvent molecules do not have enough time to re-orient themselves to a stable configuration
- This means that less energy is released when demoting the molecule from back to
- Hence, in practice, emission gives out less energy than expected
- We can therefore conclude that molecules absorb photons of higher energy and emits photons of lower energy
- The combined effect causes the absorption peak and emission peak to deviate
Why are the photons absorbed are higher in energy than the photons emitted ?
- Another way to phrase this question would be why are the absorption series trialing off to a higher energy, while the emission series are trailing off to a lower energy
- This can be easily explained by looking at the diagram below
- Hence, the absorption and emission spectrums trail off in the opposite direction
Why are the relative intensities of the peaks in each spectrum mirroring each other ?
- There are two aspects to this questions:
- Why do the two spectrums have a similar overall intensity
- Why do the two spectrums have similar relative intensities
- To answer these two question, we must return to Fermi's Golden rule
- The rate constant of the absorption and emission is directly proportional to the intensity of absorption and emission respectively
- The Franck-Condon factor and the tunneling coefficient for absorption and emission are the same because of the modulus square
- The tunneling coefficient is the same for all the transitions, so it determines the overall intensity
- The Franck-Condon factor is different for each individual transition, so it determines the relative intensities
¶ Quantum Yields
When a molecule is in its excited state, a number of processes can take place
We want to know how much of each process is taking place, so we define the quantum yield of a particular process as a ratio of rate constants
- : quantum yield of a process
- : rate constant of said process
- : sum of rate constant of all processes
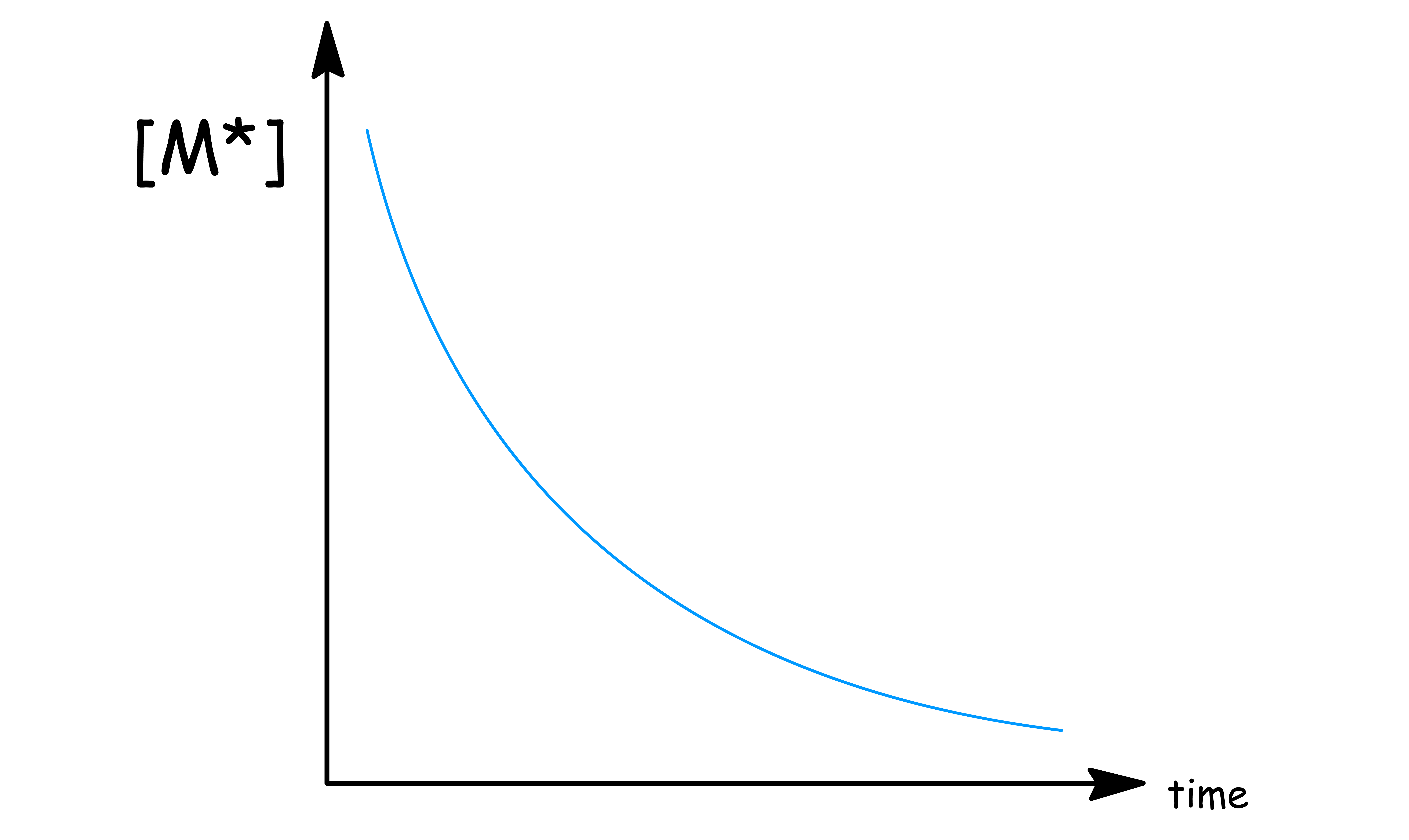
For unimolecular processes (fluorescence, internal conversion, intersystem crossing and unimolecular reactions), we can write down a rate equation
- This is a first-order differential equation, so we can easily solve it by integrating both sides
- This means that the concentration of decays exponentially with time
A parameter that is closely related to rate constant is life-time
- Life-time ( ) is defined as the time required for the concentration to drop to of its original concentration
- We can substitute this relation into the rate equaiton
- A little bit of algebaric manipulation allows us to produce an expression of
- We arrive at the conclusion that the life-time is just the reciprocal of the rate constant
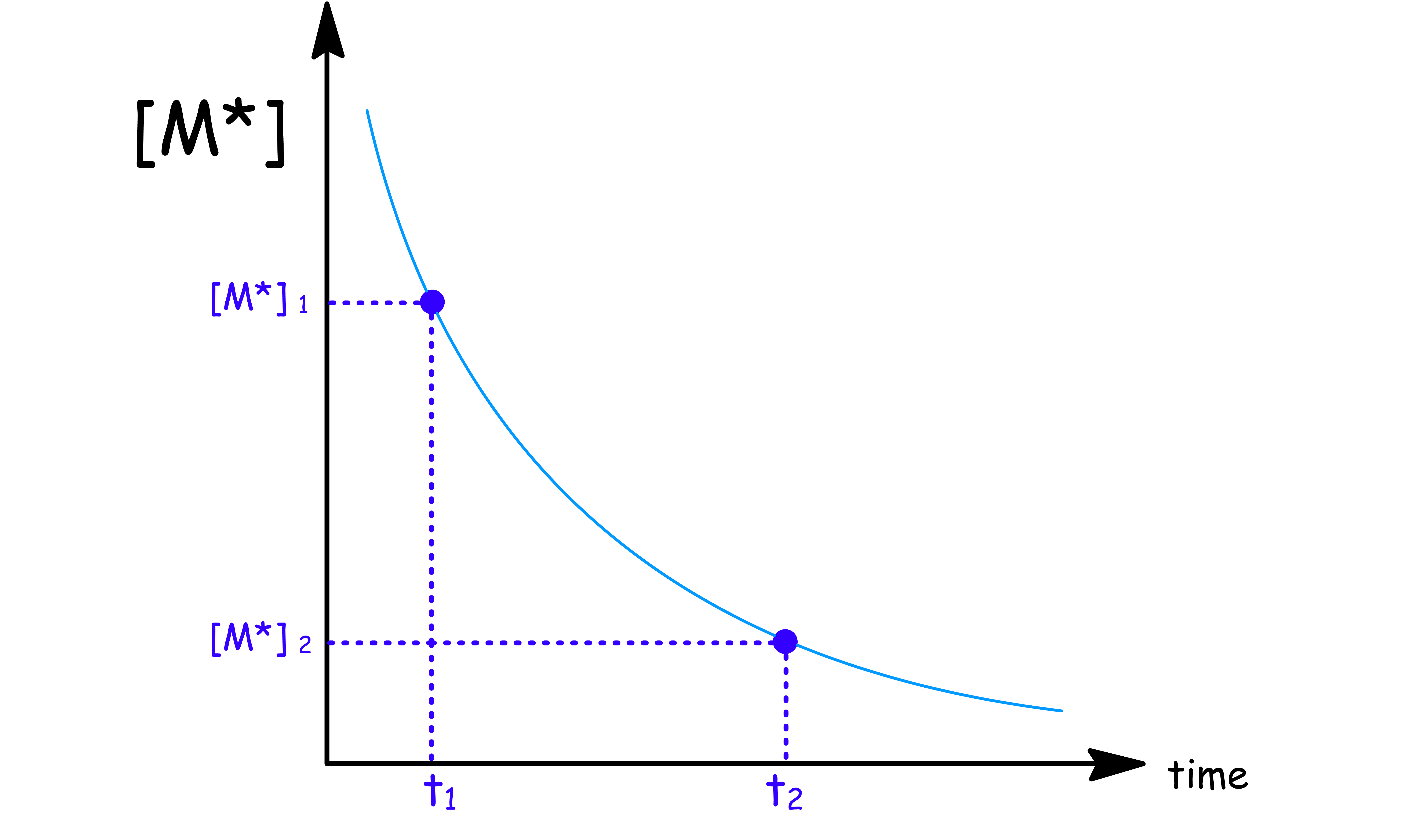
Given a graph of concentration against time, we can easily deduce the rate constant ( )
- All we need to do is to select two points on the graph and estimate the time and concentration
- We have an equation for each point
- We can then divide one equation with another and do some algebaric manipulation to obtain the relation
- This method allow us to easily determine the rate constant of fluorescence ( ) as well. This is because the intensity of fluorescence is directly proportional to the concentration of the excited state
¶ Photochemical Reactions
¶ Unimolecular Photochemical Reactions
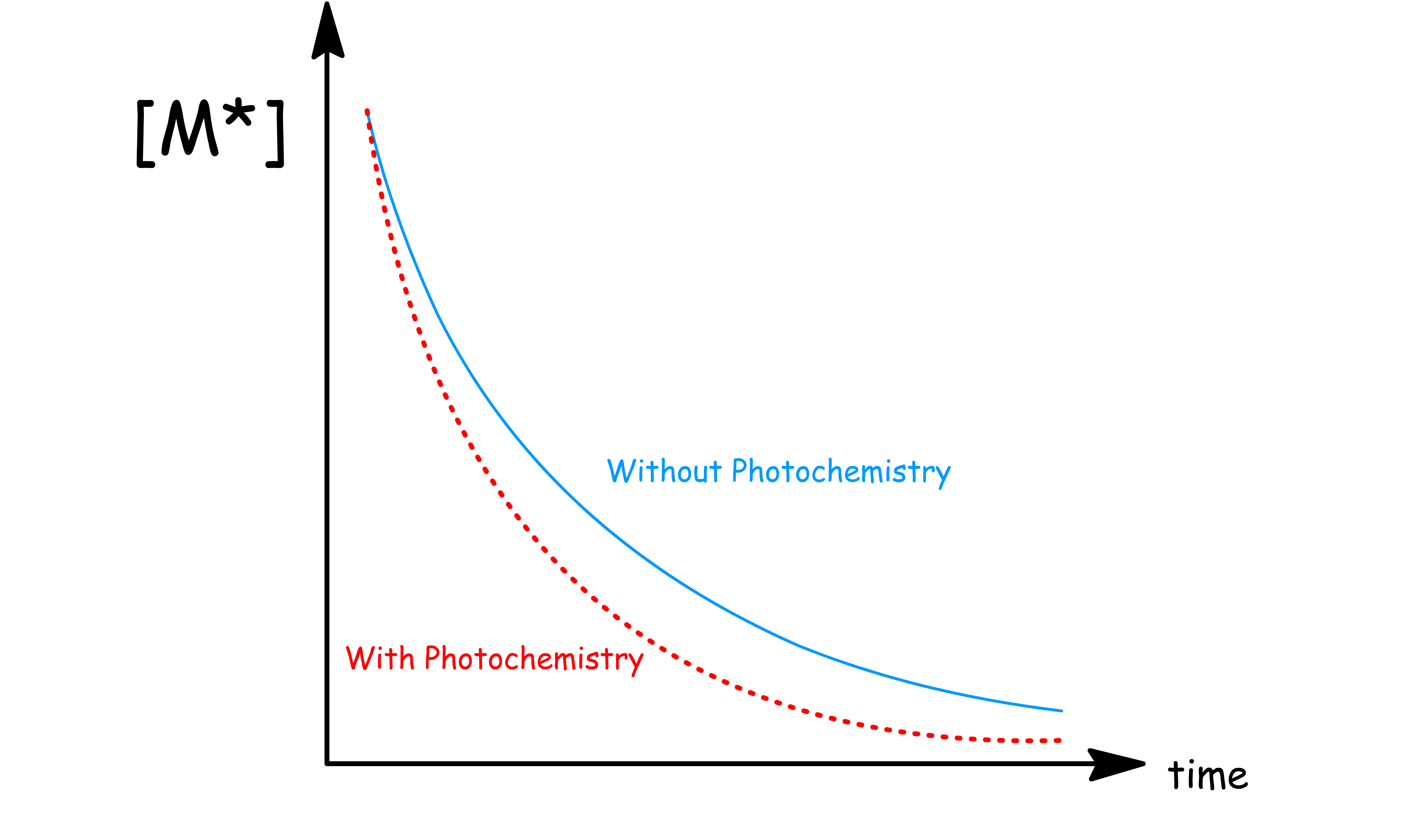
Unimolecular photochemical reactions are first-order reactions, where the rate of reaction is the product of the rate constant and the concentration of the excited state
- In the presence of photochemistry, the total decay rate () of the excited state increases as there is now one additional pathway
- In other words, the concentration of the excited state will decay faster in the presence of photochemistry
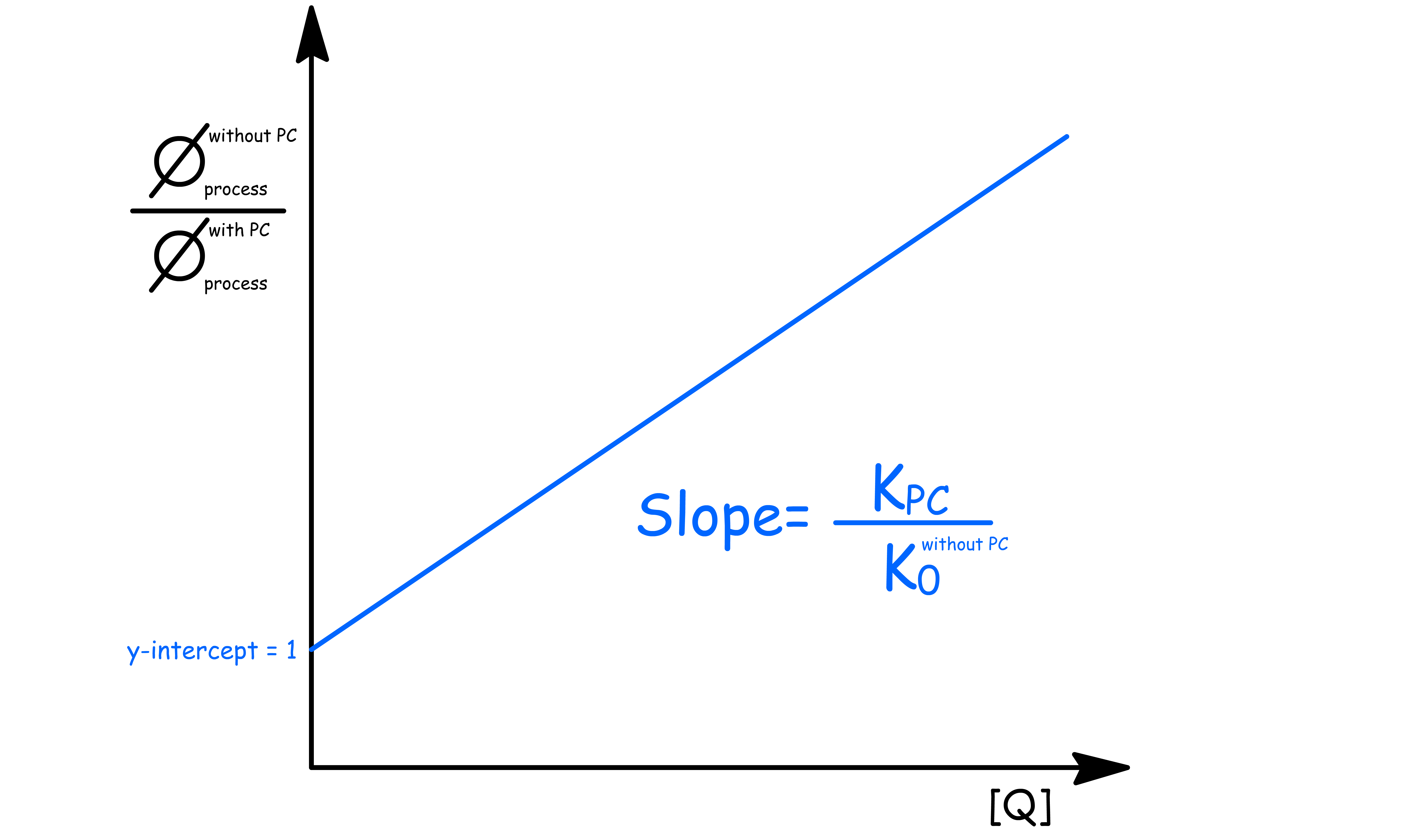
We can determine the rate of the unimolecular photochemical reaction
- Suppose we have the quantum yield of a process with photochemistry and without photochemistry
- The ratio of the quantum yield will be the ratio of the lifetimes
- In particular, for the quantum yield of fluorescence, we can relate it to intensity as well
Two important relations
- We can relate the quantum yield of photochemistry with the quantum yield of any other processes
- We can relate the rate of the photochemical reaction with other rates
¶ Bimolecular Photochemistry
Bimolecular reactions require collision of molecules
- For the bimolecular reaction , the rate is given as
- Typically, the concentration of the quencher is significantly greater than the concentration of the optically excited state. Hence, at any given time, there are a lot more quencher molecules than excited states in the reaction vessel
- In other words, the consumption of the quencher is insignificant and thus the concentration of the quencher remains mostly constant
- We can therefore treat the concentration of the quencher as a constant and combine it with the actual rate constant to get an effective rate constant
- A bimolecular photochemical reaction can therefore be treated as a pseudo-first-order photochemical reaction
Bimolecular photochemical reactions usually involve triplet states (T1) instead of singlet states (S1)
- The lifetime of singlet excited state is usually very short, usually much shorter than that of the time needed for diffusion
- Hence, most of the singlet states will have already decayed back to the ground state before a collision can happen, which makes photochemical reaction nigh impossible
- However, triplet states have a much longer lifetime since is spin-forbidden. Hence, the lifetime of triplet state is usually slower than the time needed for diffusion to take place
- As such, bimolecular photochemistry normally originates from triplet state rather than singlet excited states
We can track the progress of bimolecular photochemistry by emission measurements
- With a little mathematical manipulation, we obtain the relation
We can then plot a straight-line graph of versus
¶ Electron and Energy Transfer
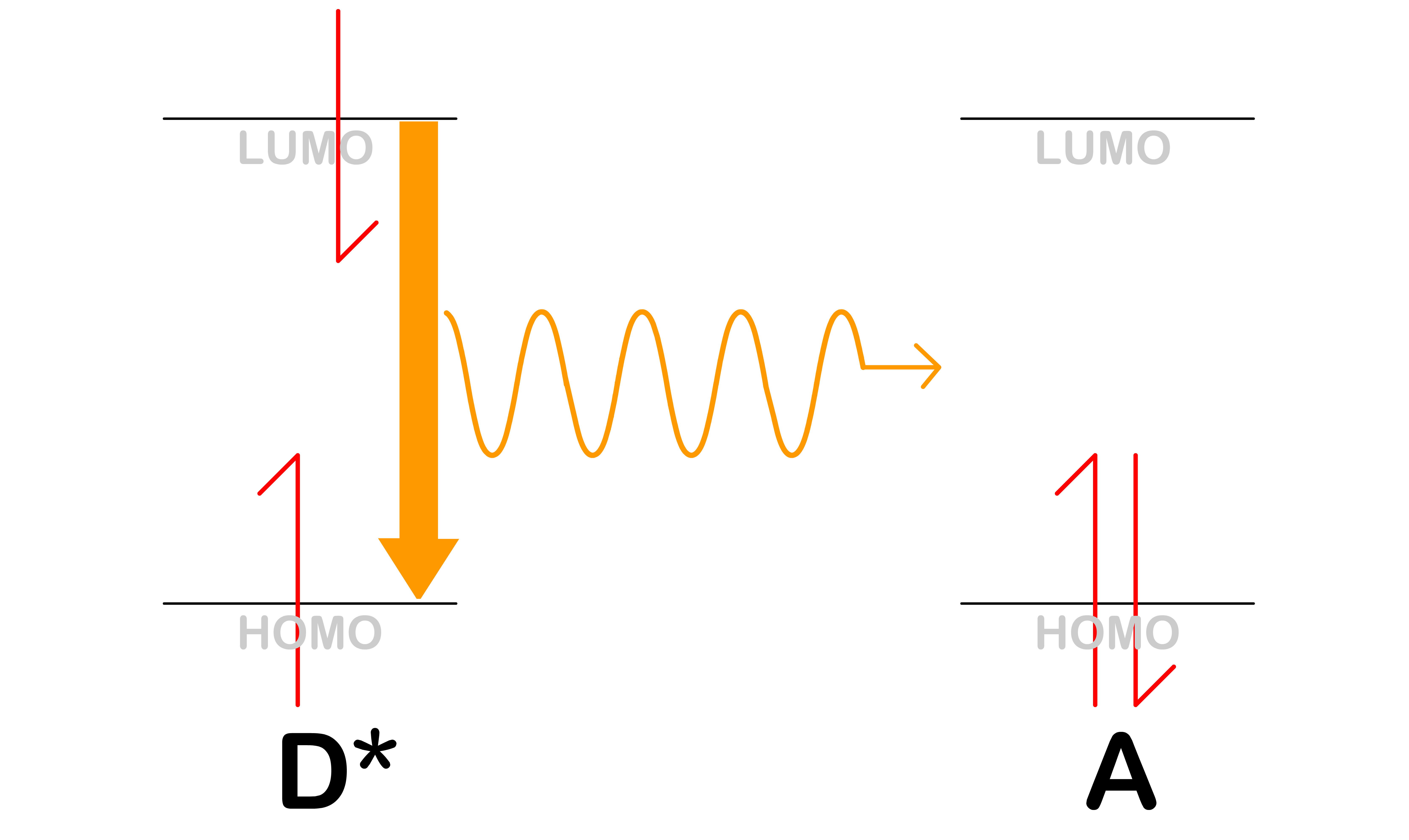
Electron transfer and energy transfer are processes that involves a donor in the excited state and an an acceptor in the ground state
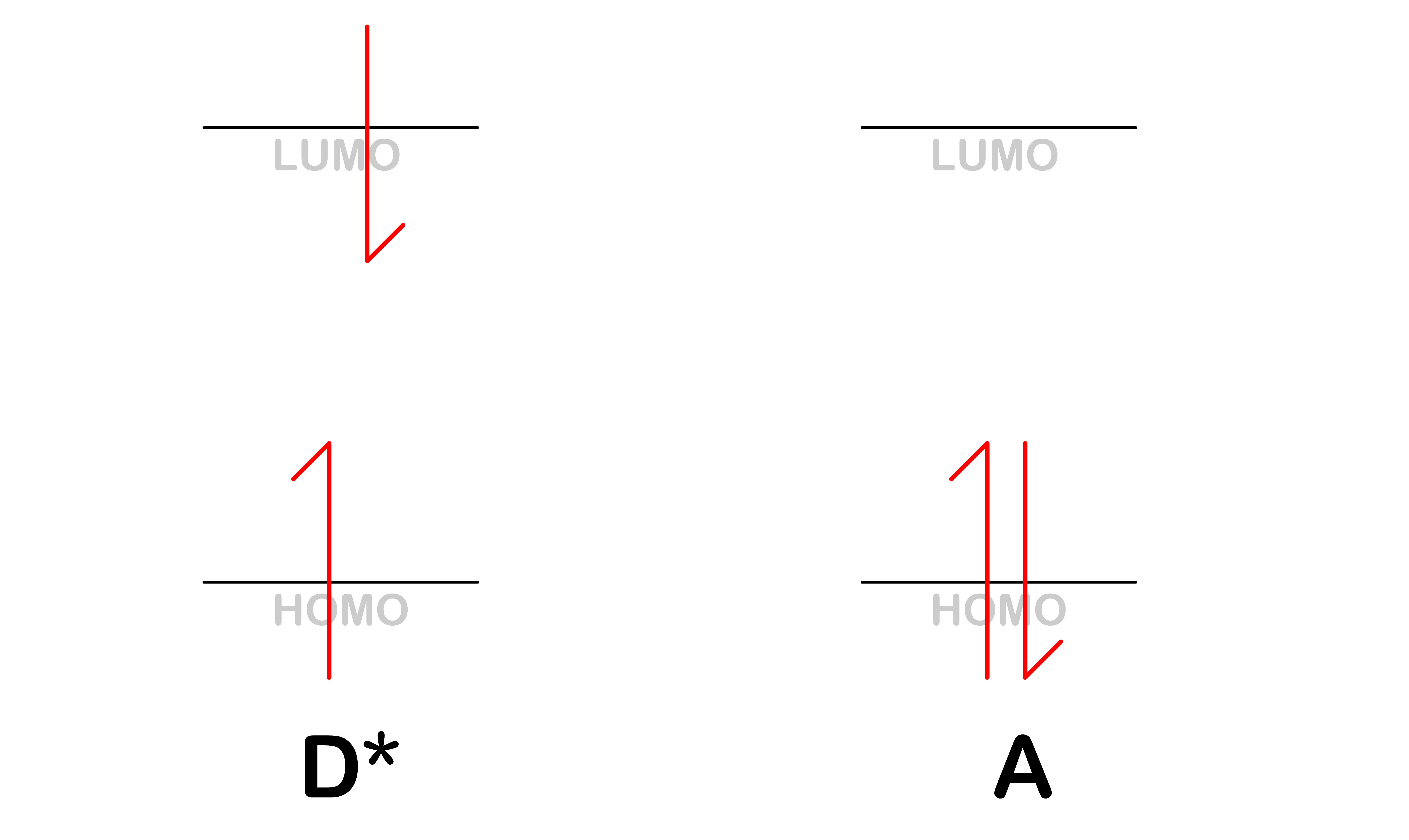
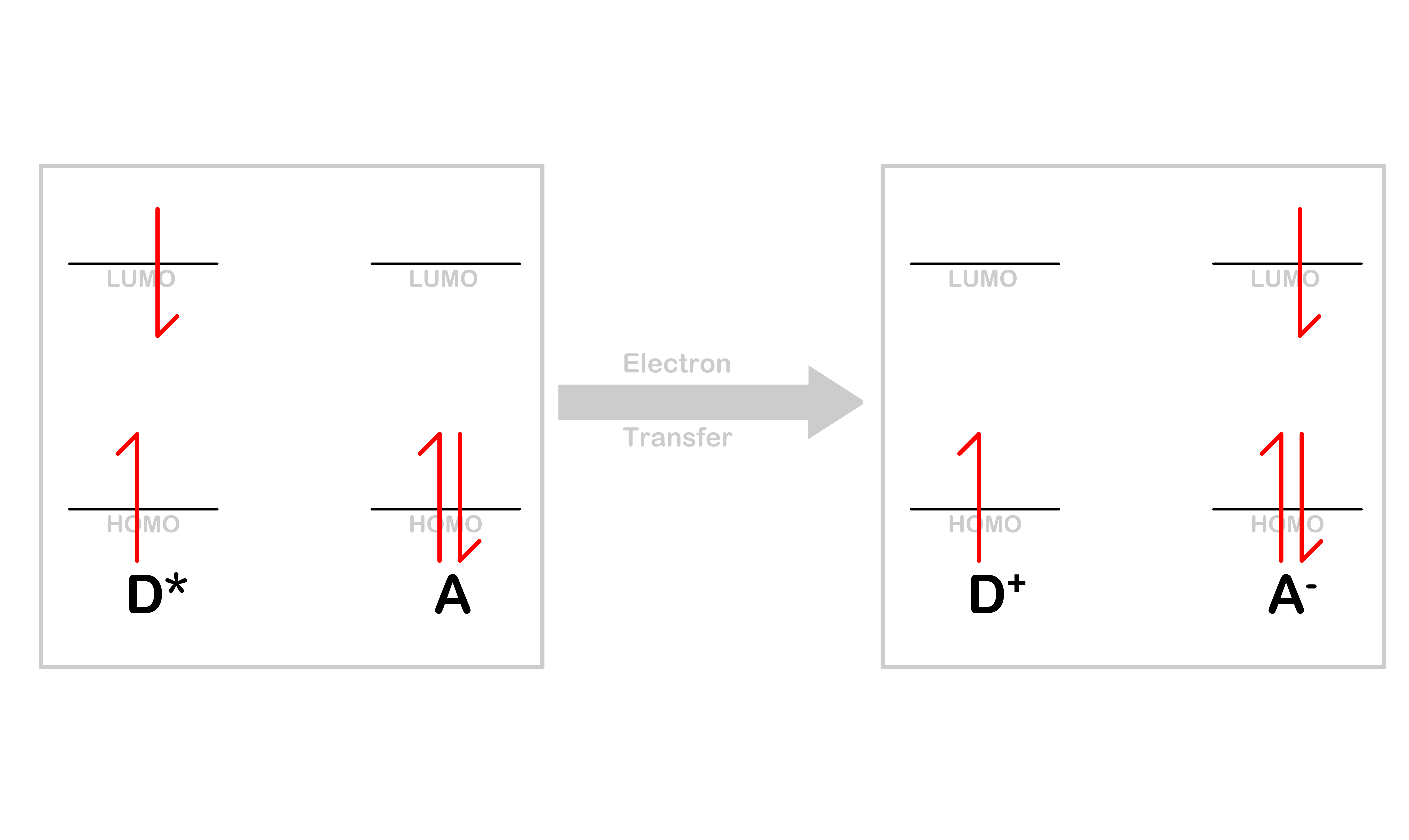
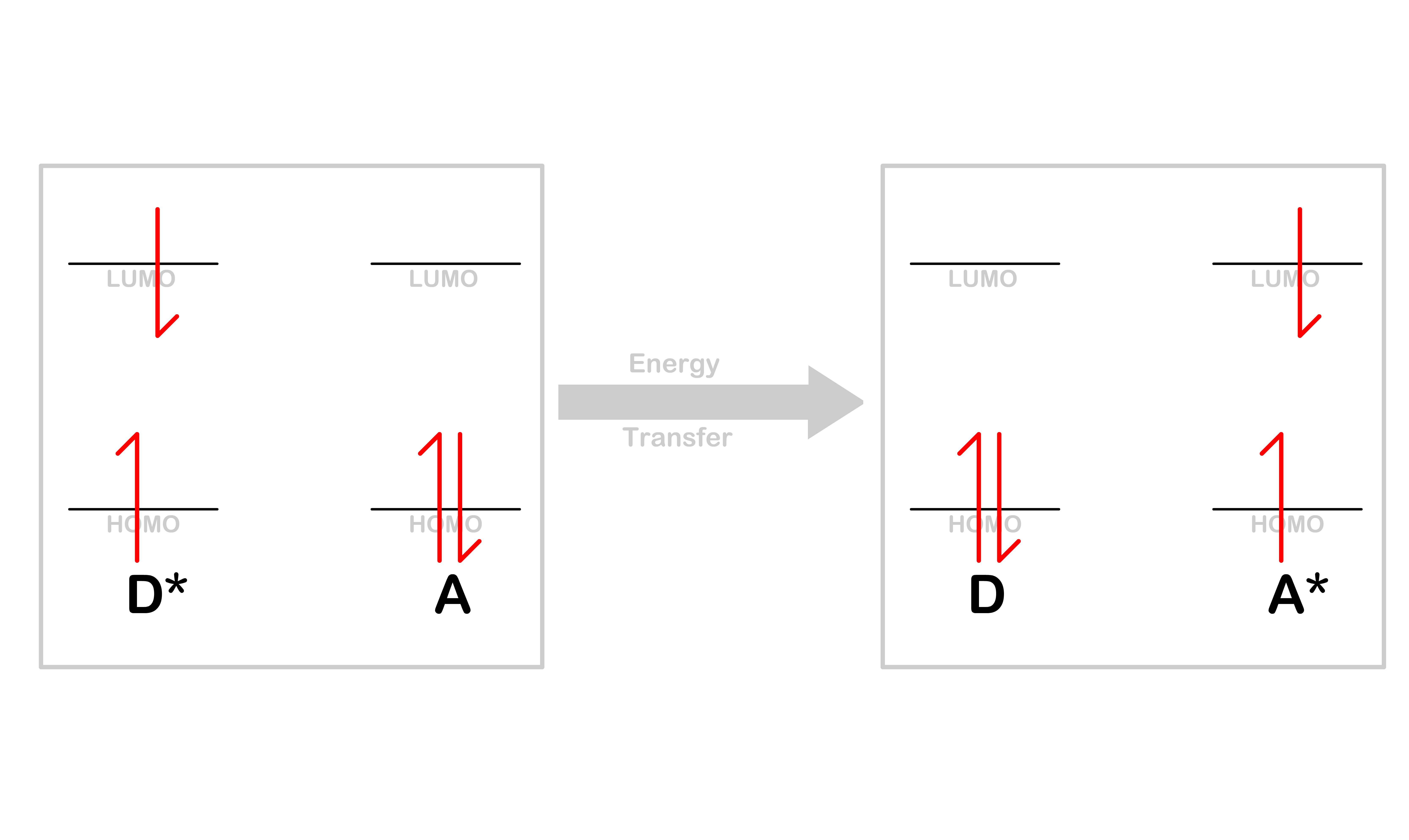
Electron Transfer
- Electron transfer is a process where the electron in the LUMO of is transferred to the LUMO of
- After the transfer, the donor will become a cation, , while the acceptor will become an anion, A^
Energy Transfer
- Energy transfer is a process in which the donor will decay from the excited state to the ground state, while the acceptor will be promoted from the ground state to the excited state
- After the transfer, the donor will be in its ground state, while the acceptor will be in its excited state
¶ Electron transfer
The rate of electron transfer is governed by Fermi-Golden Rule
- The Franck-Condon Factor (FC) is concerned with whether the transition conserves the total energy of the system
- The Tunneling Coefficient is concerned with whether the transition is favorable if the requirement for conservesation of energy is met
¶ The Franck-Condon Factor
- The Franck-Condon Factor is concerned with whether the transition conserves the total energy of the system
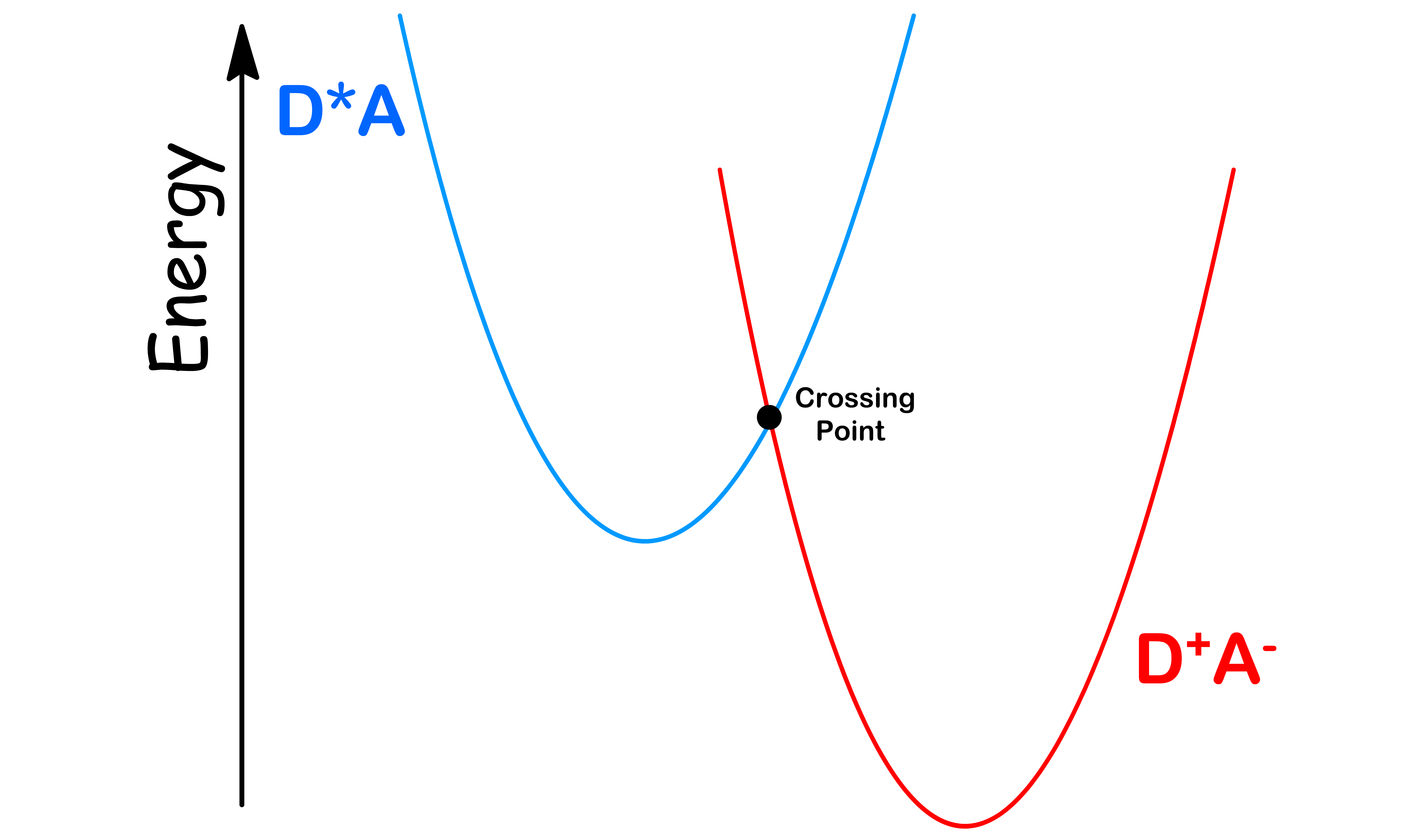
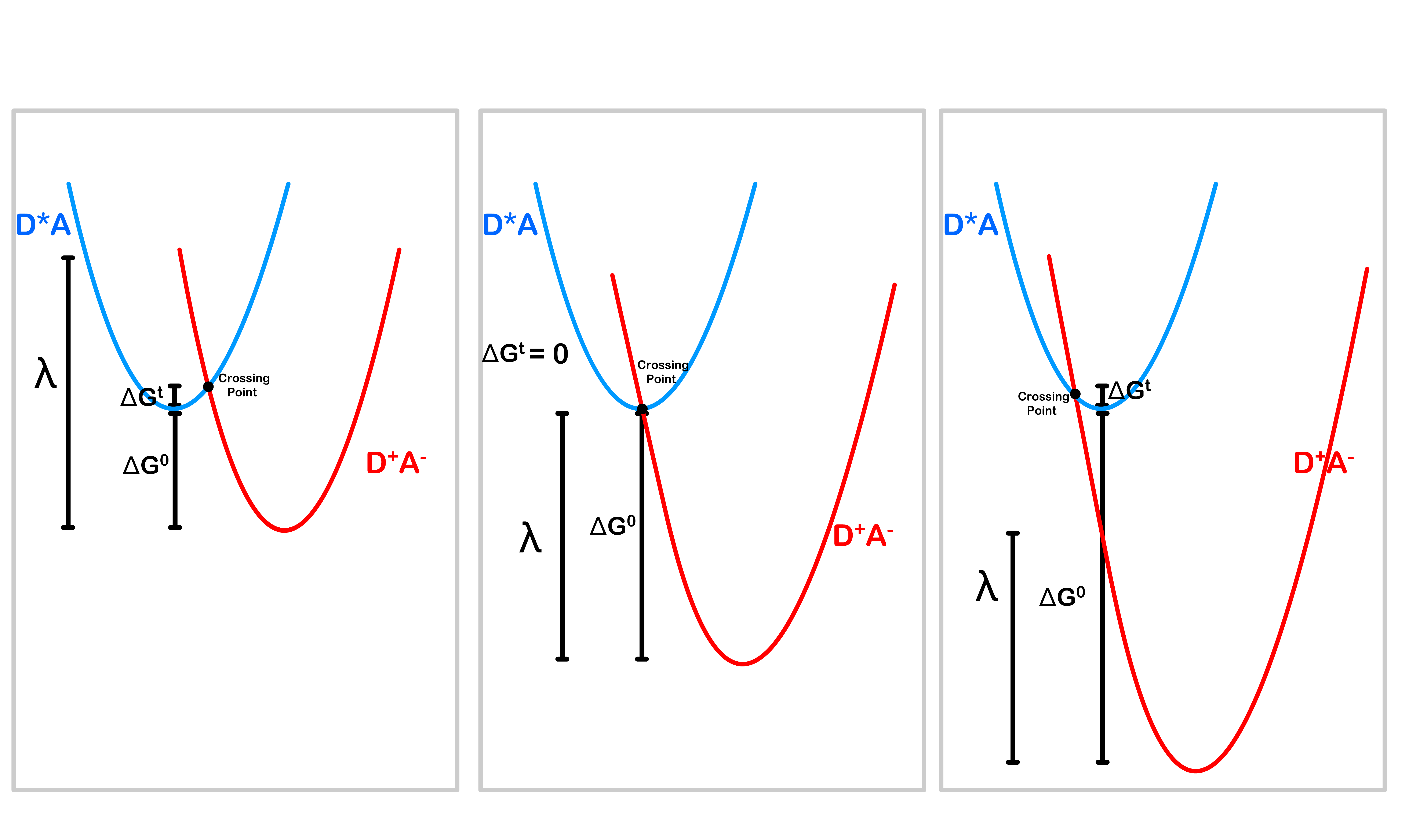
- Hence, electron transfer is only possible when \text{Energy of } D^*A = \text{Energy of } D^{\oplus}A^
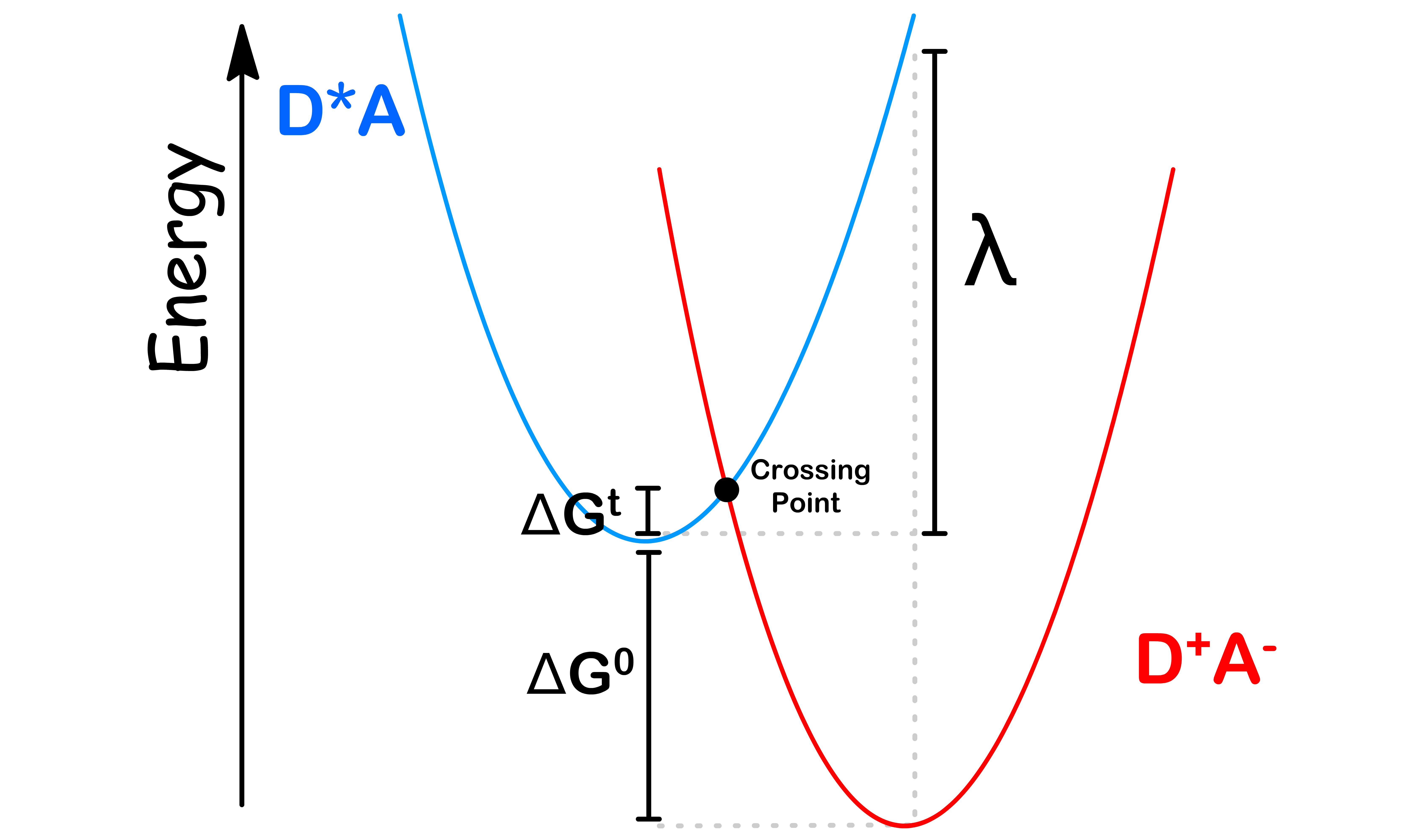
- The particular nuclear position where both the reactants and products curves have the same energy, this is referred to as the ‘crossing point
- The Franck-Condon Factor therefore measures the likely hood for to be in a state corresponding to the crossing point. We can use the Boltzmann distribution to measure this probability
Without Derivation
- The activation barrier ( ) can be expressed in terms of the free energy ( ) driving force for the reaction
- The FC term for electron transfer can therefore be written as follows
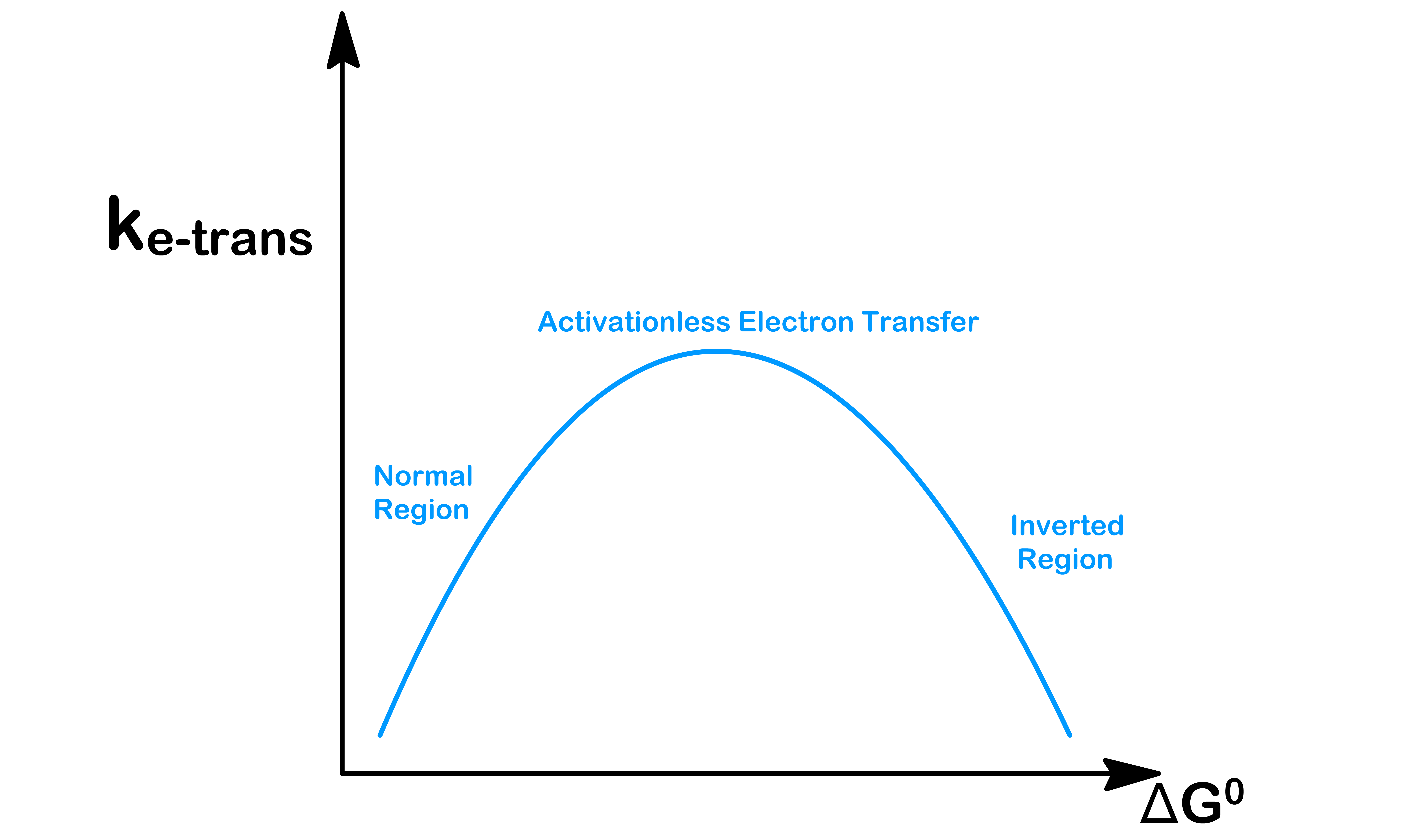
- As the free energy ( ) increases, the activation energy also changes ( )
- We can therefore plot a graph of the rate of electron transfer against the free energy
- The rate is highest when
¶ The Tunneling Coefficient
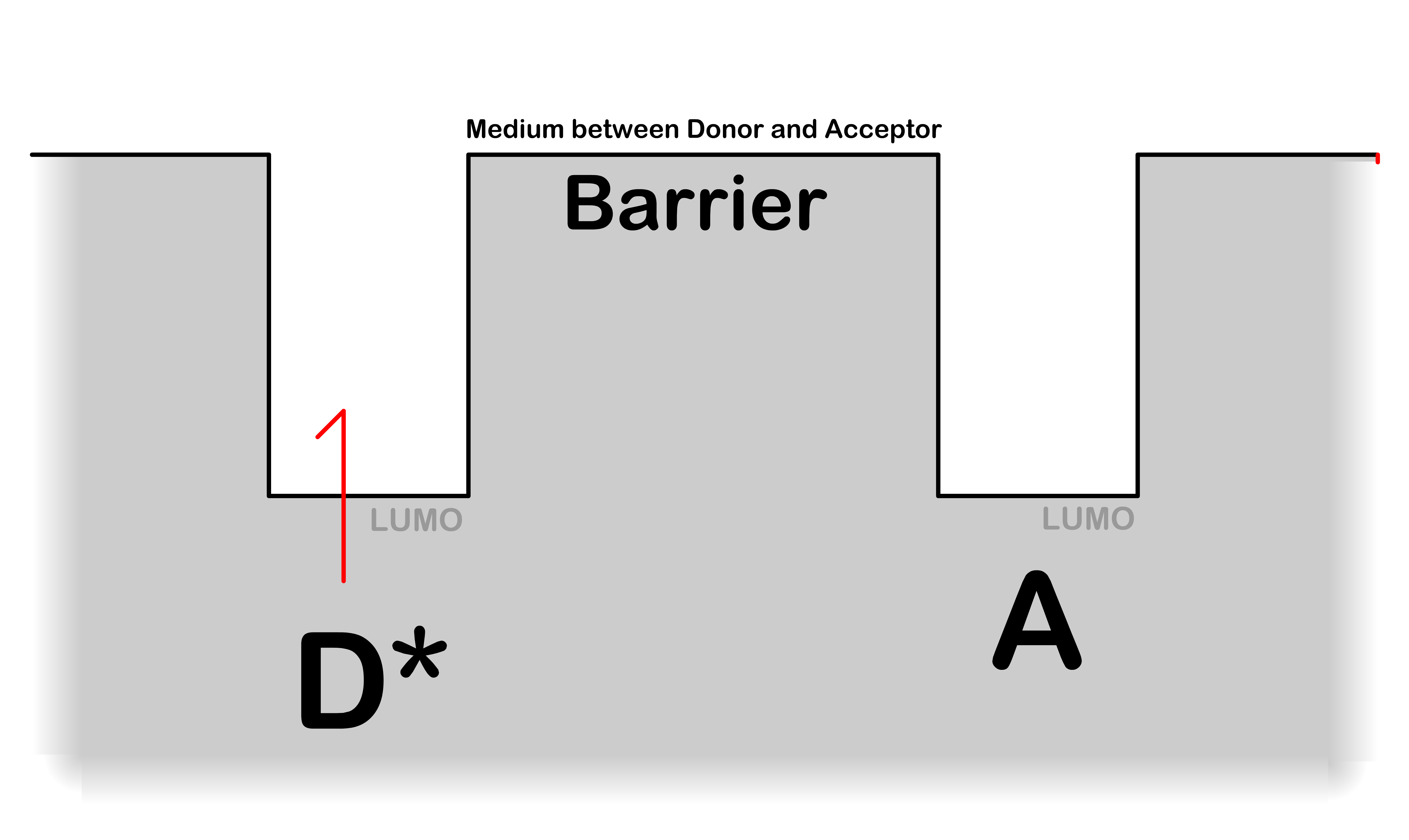
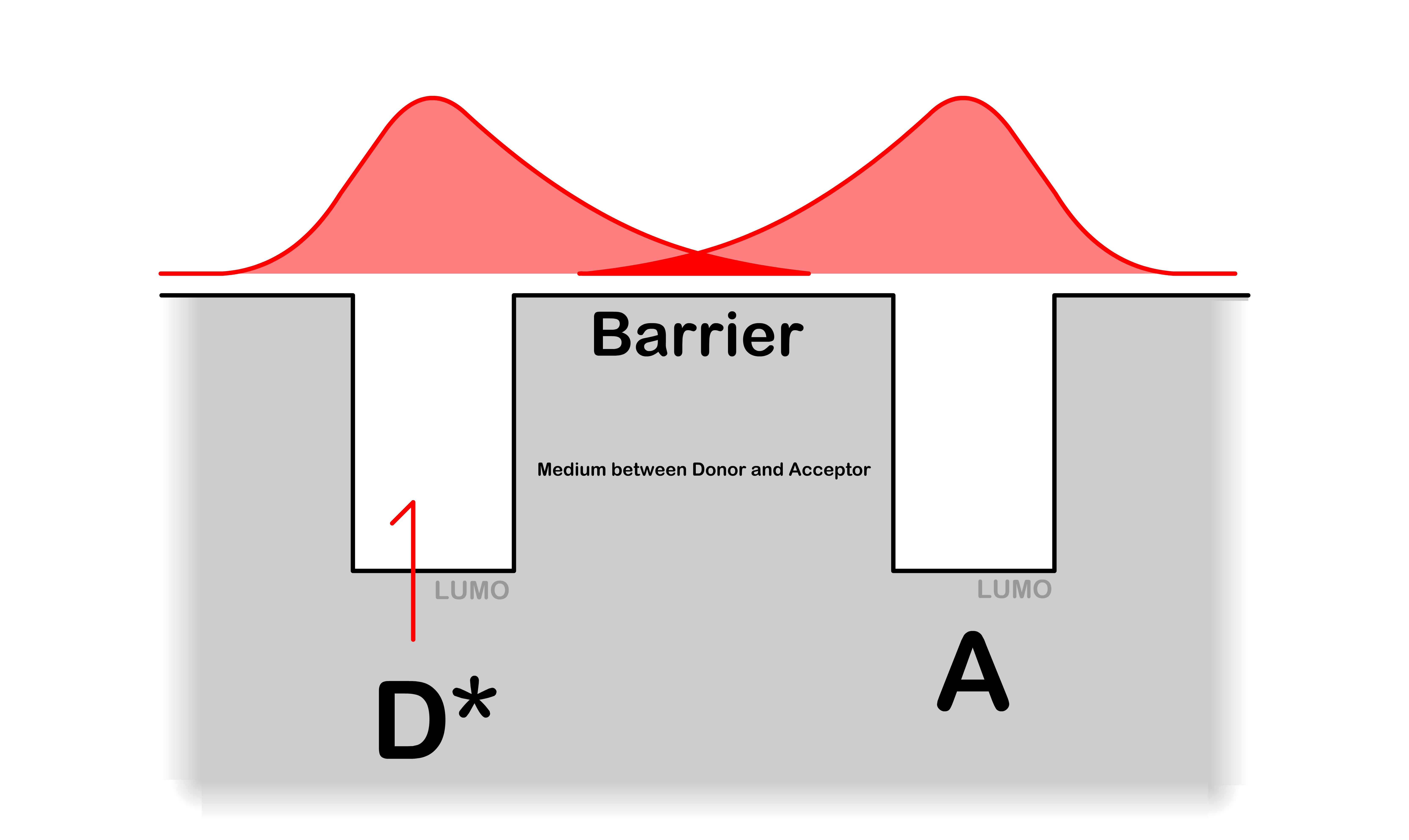
- The tunneling coefficient tells us how likely the electron in the LUMO of is going to "tunnel" through the barrier and appear in the LUMO of given that energy is conserved
- The more the electronic wavefunction of overlaps with , the higher the chance of tunneling
- The overlap of electronic wavefunction can be mathematically expressed as an inner product
- It turns out the integral is proportional to an exponential. This is related to the eigenfunction of hydrogenic systems (check derivation here)
- We can further simply the expression
- is a positive number that measures the ability of the electron to tunnel through the medium between the donor and acceptor
The smaller is, the easier it is to tunnel through the barrier
- is close to zero when the potential energy of the medium is low (e.g. π system) and is large when the potential energy of the medium is high (e.g. vaccum)
¶ Energy Transfer
¶ Trivial Mechanism
- The donor decays and emits a photon, which is then absorbed by the acceptor
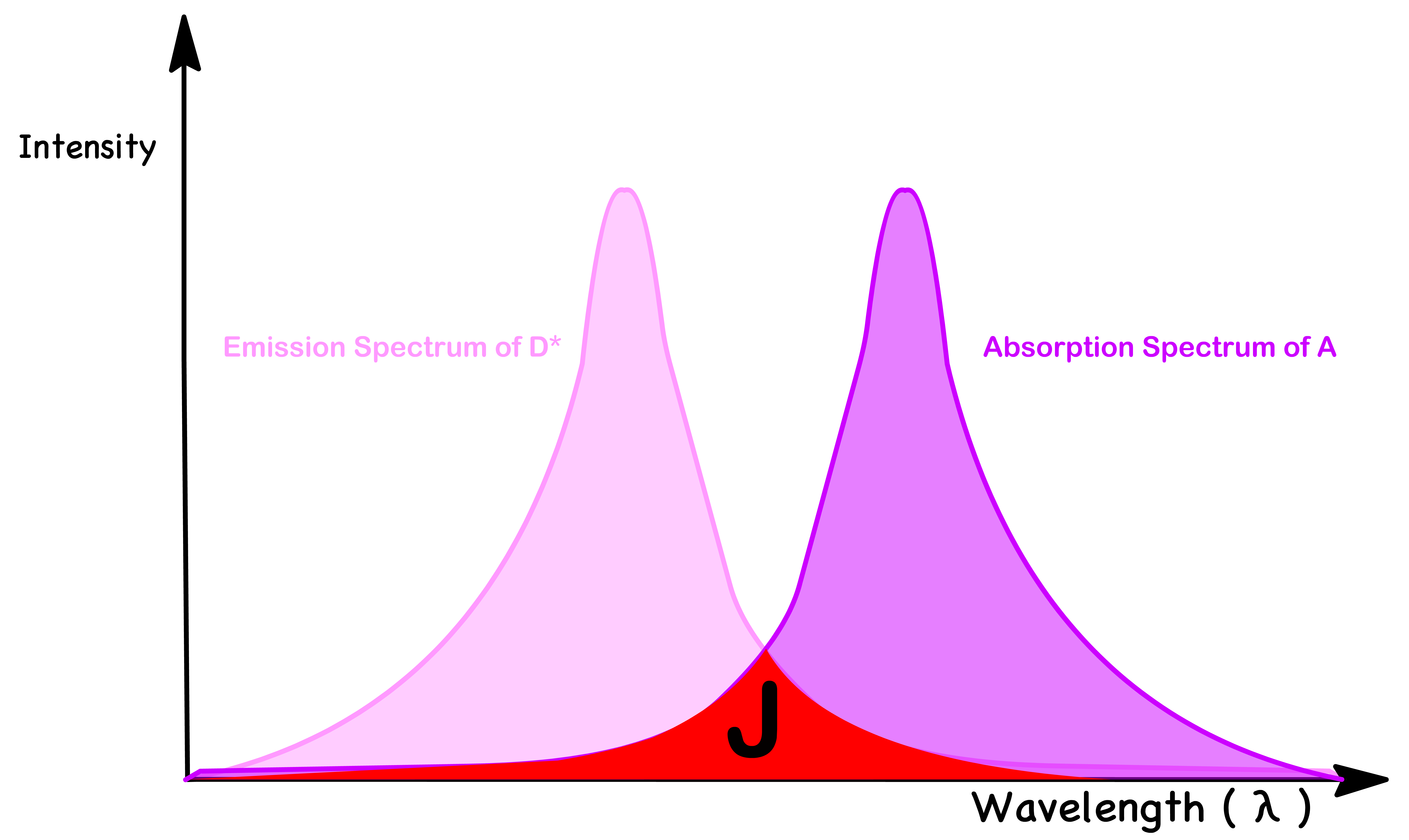
- Efficient trivial energy transfer requires good overlap between the emission spectrum of donor and absorption spectrum of acceptor. This is to ensure that the acceptor molecules are able to absorb photons emitted by the donor
- The donor must have a large (so that it emits more photon) and the acceptor must have a large oscillator strength f (so that it absorbs more photon) in region where the donor emits
- This mechanism only works for singlet-to-singlet state energy transfer
¶ Forster energy transfer
- radiationless process
- Forster energy transfer is a Fermi-Golden rule reaction:
Franck-Condon Factor
- The Franck-Condon Factor is concerned with whether the transition conserves the total energy of the system
- The probability of isoenergetic energy levels depends on the extent of overlap of emission spectrum of donor with absorption spectrum of acceptor
- This is because the HOMO-LUMO gap of the donor and the acceptor will be of similar size when the absorption spectrum of the acceptor is similar to the emission spectrum of the donor
- Mathematically, the FC factor is given by the overlap integral (J)
Tunneling Coefficient
- The term is based on a dipole-dipole interaction
Random Derivationless Bullshits
- Combining the two terms, the rate constant for Foster energy transfer is given by
- We can simplify the expression to
- The rate constant for energy transfer depends on the relative orientation of the donor and acceptor transition dipoles
Quantum Yield
- The quantum yield of energy transfer:
- We can therefore define as the distance at which the energy transfer efficiency is 50%
- Small values imply poor donor-accepter energy transfer partners