¶ Fluid Interfaces
Until now, we have assumed that each phase of a thermodynamic system is completely homogeneous, with its intensive properties remaining constant throughout the phase
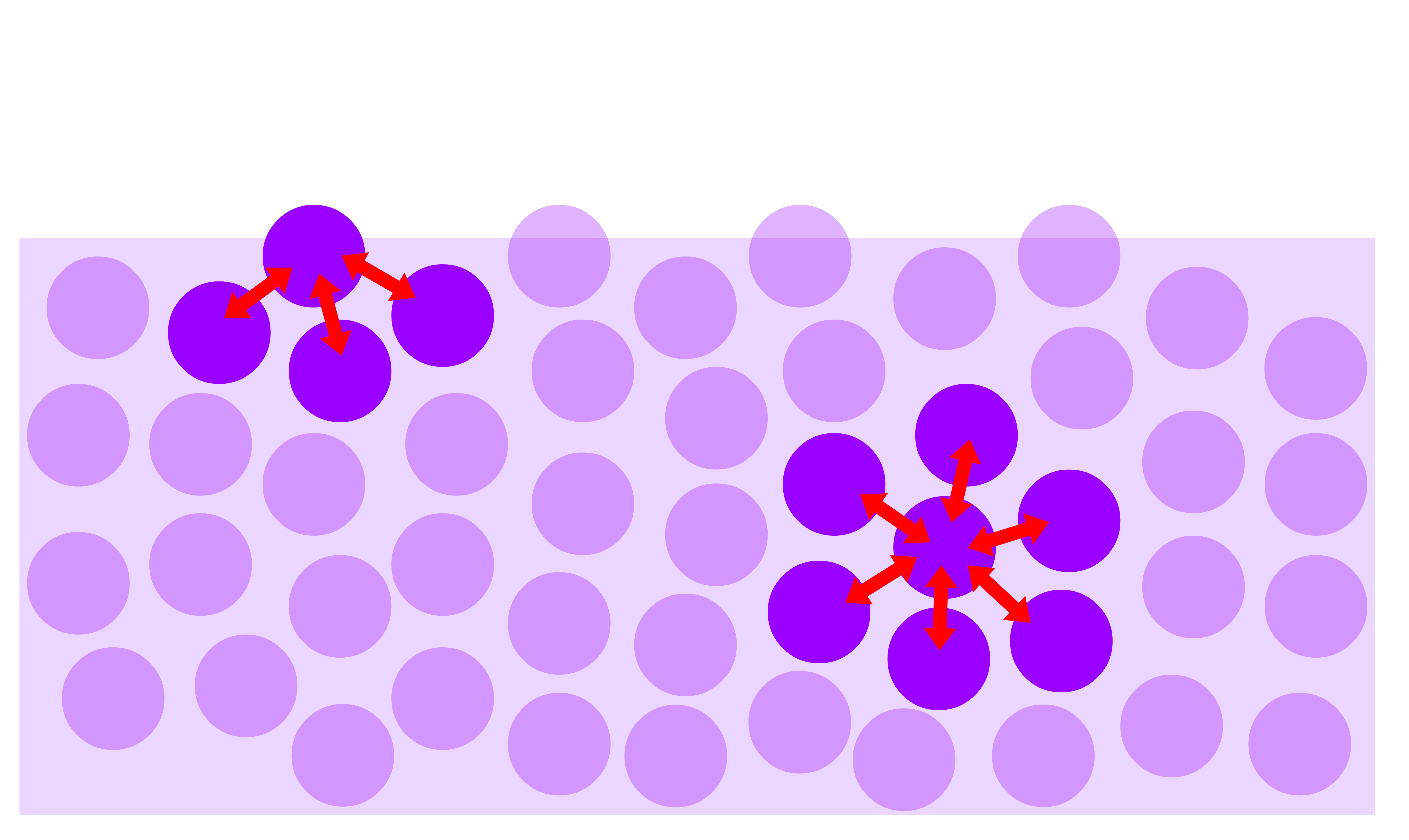
- However, in reality, molecules present at the surface of a phase experience a different environment than those located in the interior of the phase
- Molecules experience different intermolecular interactions at the surface of a phase compared to the interior, as they are surrounded by molecules from within the phase on one side and the surrounding environment on the other side
When two phases come into contact with each other, there exists a three-dimensional region called the interfacial layer, where the molecules from both phases interact with each other
- This interfacial layer is a transition region that lies between the two bulk phases and is not homogeneous in nature
- Instead, it is characterized by a mixture of the properties of the two bulk phases
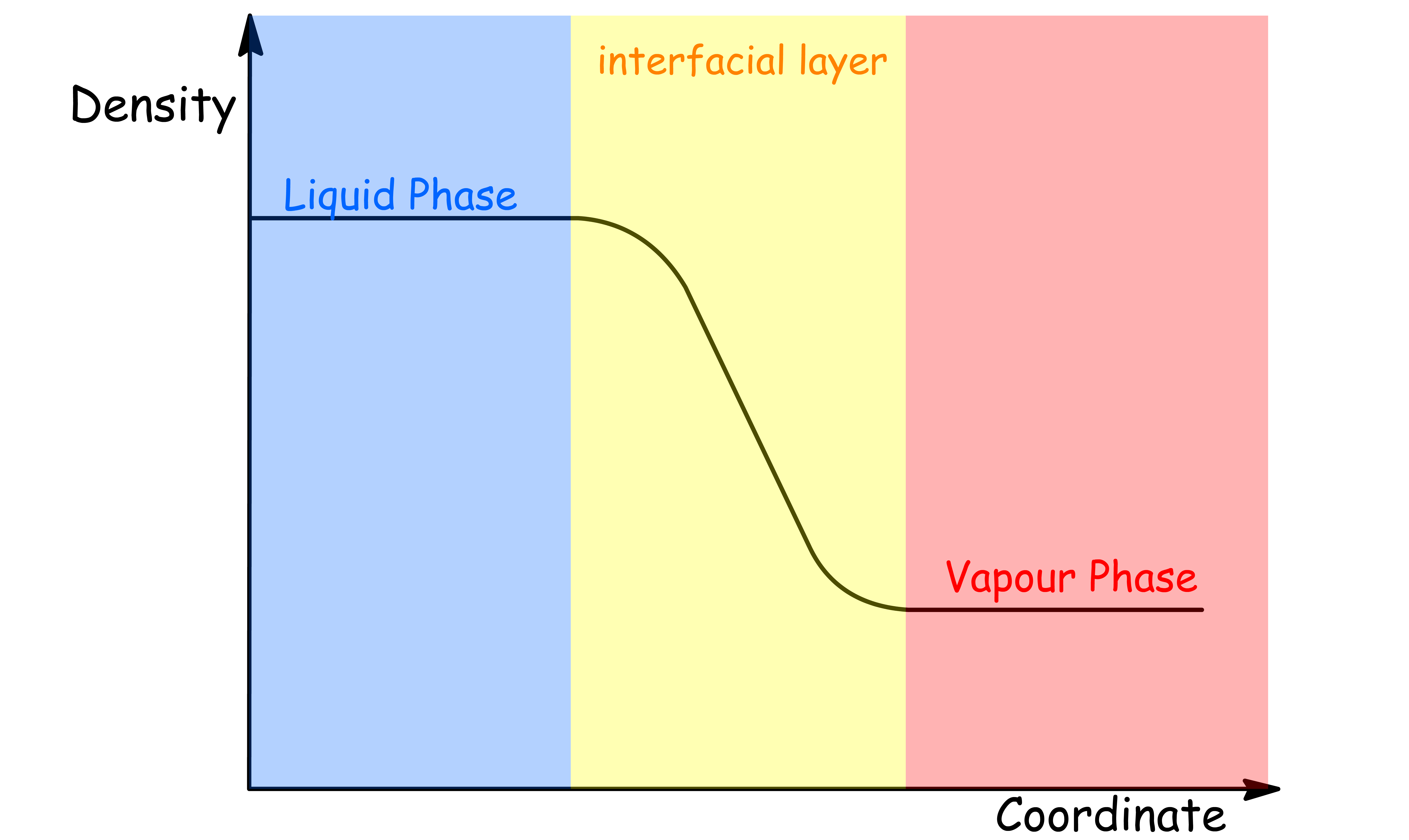
¶ Density Profile
It is easy to make the assumption that a surface have zero thickness, in the sense that the surface is composed of one layer of molecules from each phases only
- While this may be a good approximation for solid surfaces, a liquid surface is more diffuse and it is perhaps more appropriate to call it a surface region or even a surface phase
- In order to describe this surface phase properly, we shall introduce an important parameter in interfacial thermodynamics, density profile
The density profile is a measure of the distribution of molecules across the interfacial layer between two phases
- It provides information on how the density of the molecules changes as a function of distance from the interface
- The system under consideration can consist of either a liquid and a vapor phase, or two liquid phases
¶ Density Profile for Liquid-Vapour interface
- The density decreases from the liquid to vapour phase
- The smooth variation is due to thermal fluctuations
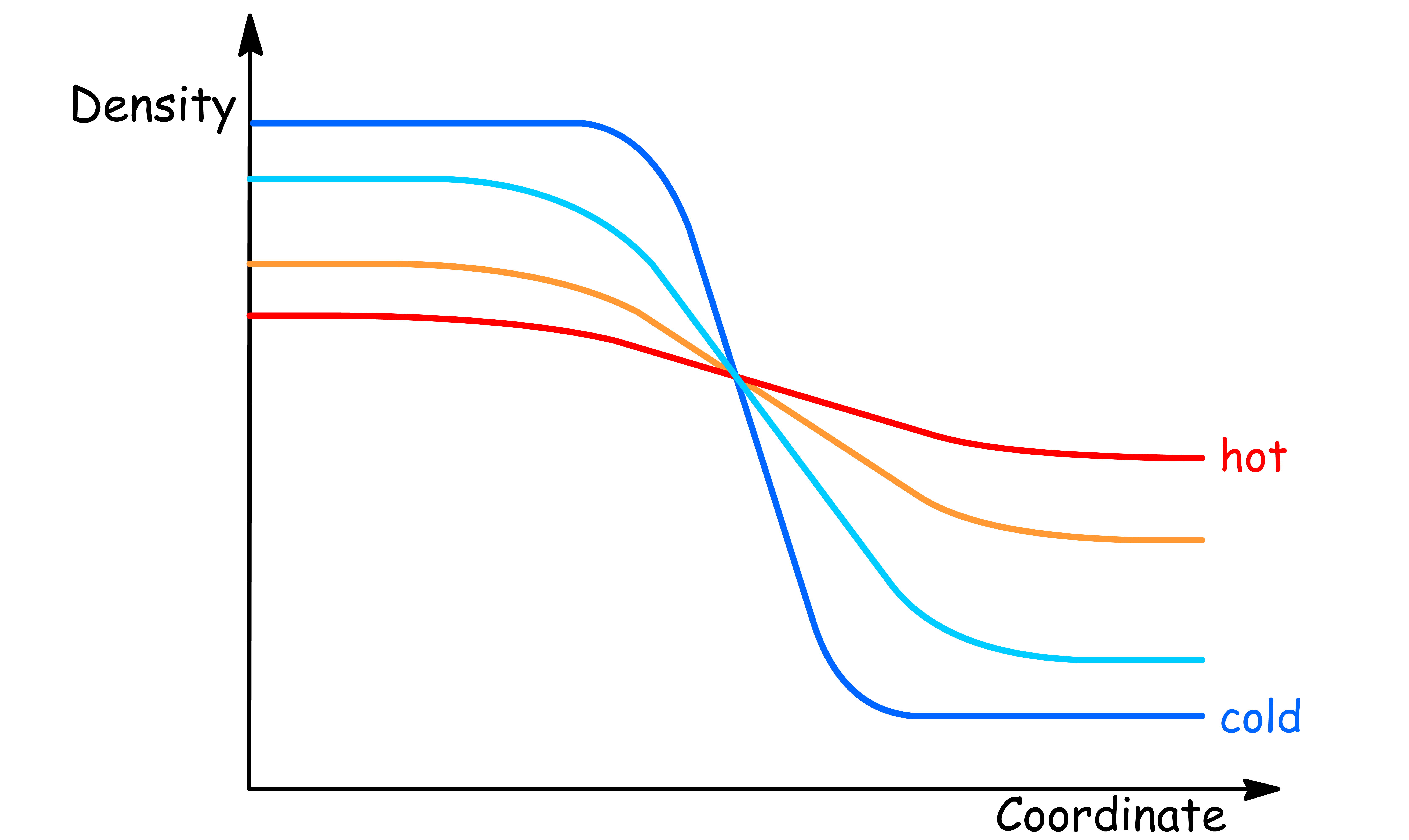
Temperature-Dependence
Boiling does not occur when a liquid is heated in a rigid closed vessel
The difference in density between liquid and vapour decreases with increasing temperature
- The vapour pressure, and hence the density of the vapour, rises as the temperature is raised
- The density of the liquid decreases as a result of its expansion
There comes a stage when the density of the vapour is equal to that of the remaining liquid and the interface between the two phases disappears>
- The temperature at which the interface disappears is the critical temperature
- At the critical temperature, the properties of the liquid and vapor phases become identical, and the substance exhibits characteristics of both a liquid and a gas
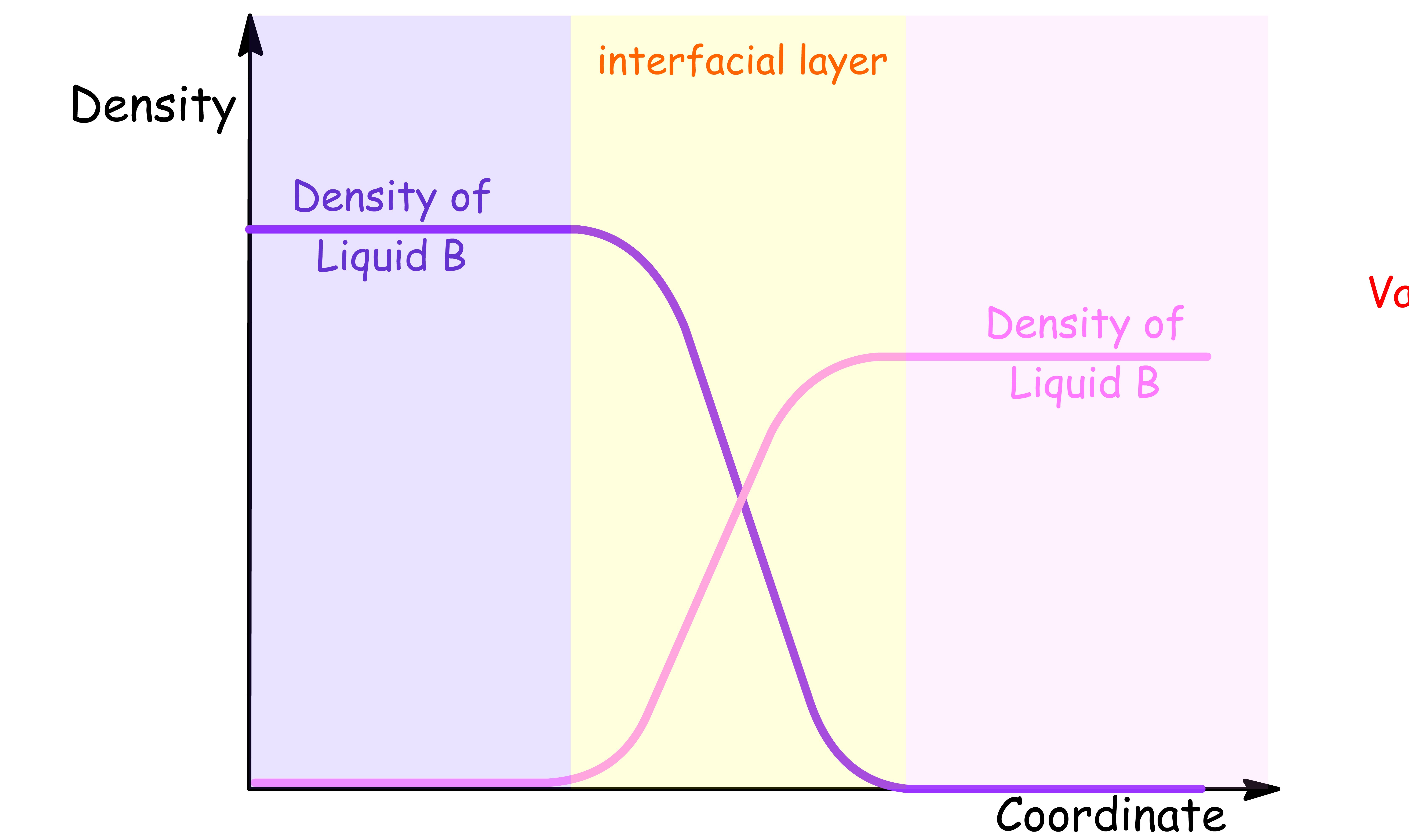
¶ Density Profile for Liquid-Liquid interface
- At the liquid-liquid interface, there is a sharp change in the density profile between the two liquids
- The density of each liquid approaches a constant value far away from the interface, but in the interfacial region, there is a gradual transition in density between the two liquids. This interfacial region is often referred to as the diffuse layer, and it can be described by the width of the density profile
Temperature-Dependence
The temperature dependence of the density profile for a liquid-liquid interface near the UCST can be particularly interesting
At the UCST, the two phases have the same composition, which means that they have the same density
- In other words, there is no density difference between the two liquids at the interface
¶ Surface Tension
Molecules located at the surface of a liquid phase experience weaker intermolecular attractions when compared to the molecules present in the interior of the bulk liquid phase
- Moreover, due to the low concentration of molecules in the vapor phase, the interaction between vapor-phase molecules and molecules at the surface of the liquid can be ignored
- Consequently, molecules at the surface of a liquid experience a higher average energy than the molecules present in the bulk phase
Since it costs more energy for molecules to be on the surface than in the interior of the bulk liquid phase, it requires work to transfer the molecules from the interior to the surface to increase the area of the liquid-vapour interface
- It is generally true that positive work is required to increase the area of an interface between two phases
- For this reason, systems tend to assume a configuration of minimum surface area
- Thus an isolated drop in the absence of external force is spherical as sphere is the shape with a minimum ratio of surface area to volume
Surface effects can be expressed in the language of Helmholtz and Gibbs energy, and the link between these quantities is the work needed to change the surface area of liquid by a given amount
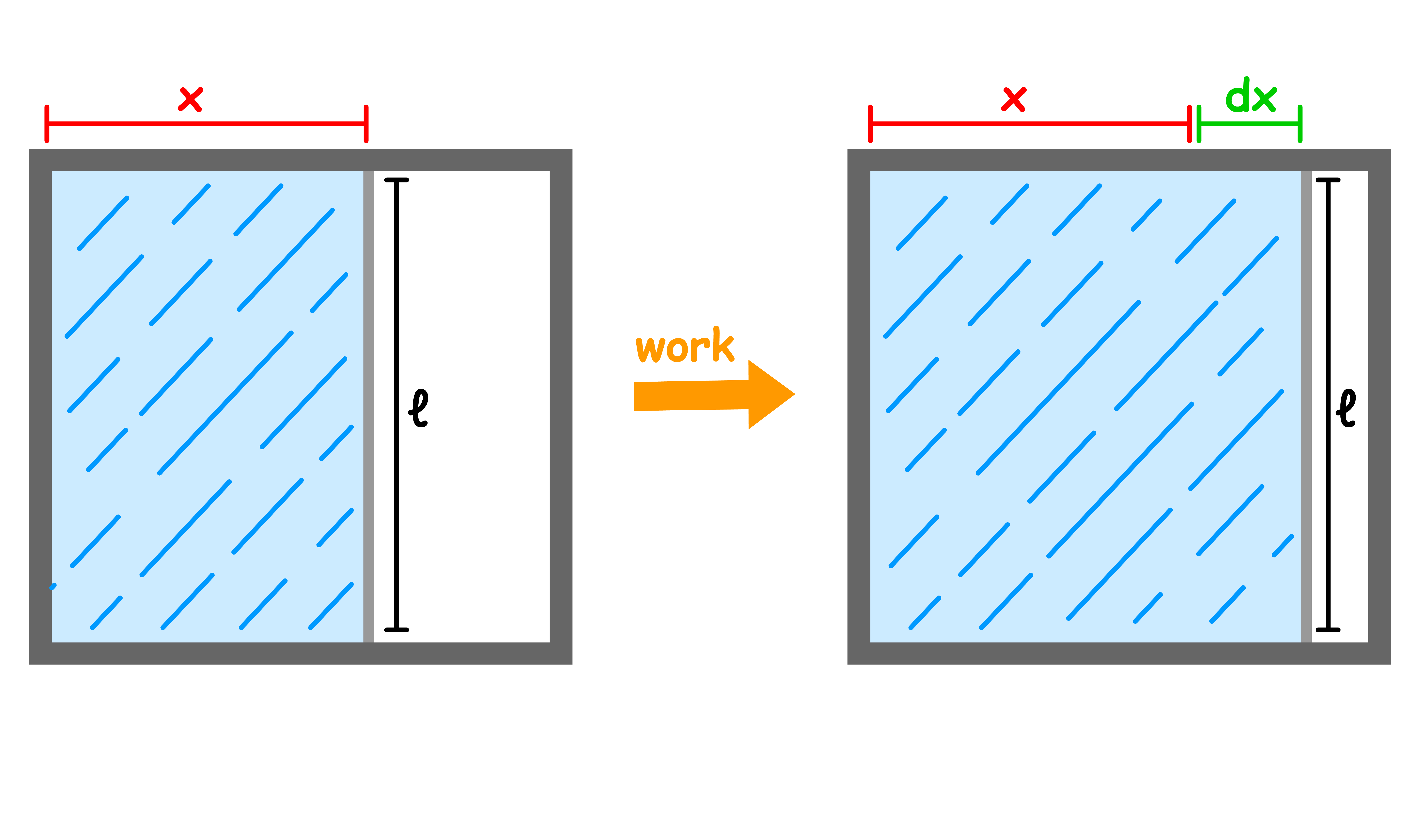
Surface Tension as a Force per Unit Length
Consider a soap film stretched over a wire frame, one end is movable
- An opposing force is exerted on the membrane when we try to stretch it
- If the value of the force per unit length is denoted by , then the work done in extending the movable membrane by a distance is
- We call the surface tension of the liquid
- Surface tension has a dimension of and its units are typically J \ m^
- Surface tension is an intensive property, meaning that it does not depend on the amount or size of the system, but only on its composition and conditions
Surface Tension and Free Energy
In thermodynamics, it is easier to communicate in terms of free energies, and so we shall express surface tension in terms of Helmholtz energy and Gibbs energy respectively
- Recall from Year 1 that work is given by the change in either Helmholtz or Gibbs energy under certain conditions
- We can therefore write
- Spontaneous processes take place with a decrease in free energy and this will happen when the area decreases ()
- This is a more formal way of saying that surfaces have a natural tendency to contract
We can also rearrange the equation and make surface tension the subject
¶ Cohesion and Surface Tension
Surface tension can also be interpreted as a measure of the energy required to increase the surface area of a liquid
Cohesive energy refers to the energy required to separate the molecules in a liquid, or the energy released when the molecules come together to form a liquid
The molecules at the surface lose half of their cohesive energy,
- The surface tension quantifies the energy loss per molecular area
- is the area of a molecule and a the factor of indicates that half of the cohesion energy is lost on the surface
Temperature-Dependence
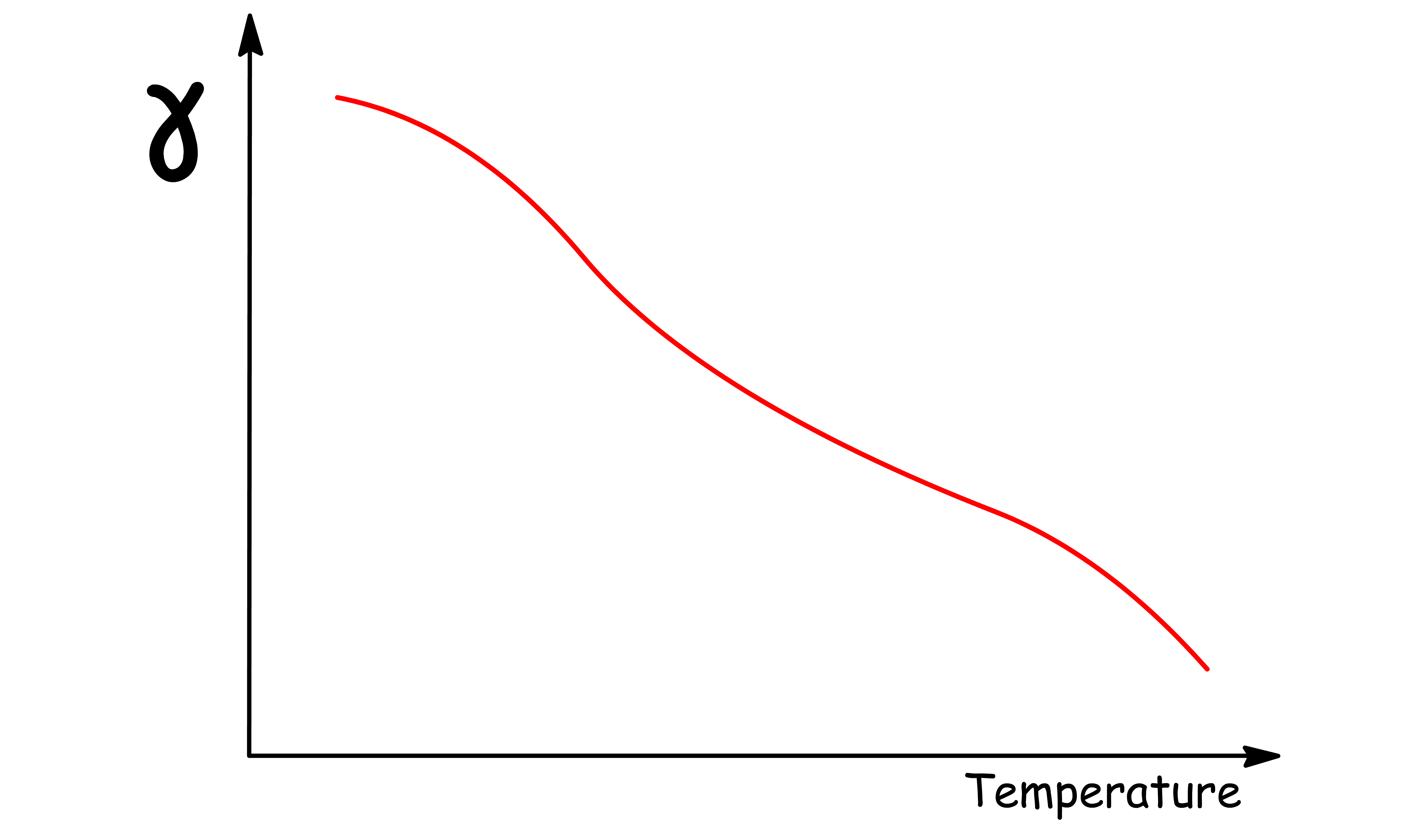
The surface tension of a liquid is inversely related to its temperature
- As the temperature of a liquid increases, the cohesive forces between the molecules weaken, and the surface tension of the liquid decreases
The surface tension decreases with temperature and it is zero at the critical point
- At the critical point, , the liquid-vapour interface disappears
- The absence of an interface means that there is no surface tension,
¶ Curved Surfaces
In this section, we will deal with two important equations: Laplace-Young Equation and Kelvin Equation
- Kelvin equation and Laplace-Young equation are two different equations that describe the behavior of liquids and their curved interfaces
- The Kelvin equation describes the relationship between the vapor pressure and the curvature of a liquid-gas interface, while the Laplace-Young equation describes the relationship between the pressure difference across an interface and its curvature
Overpressure and the Laplace-Young Equation
It turns out that at equilibrium, the pressure between two phases can be different due to the presence of a curved interface
- Consider a liquid in contact with another phase, perhaps another liquid or even gas or vacuum. Let us denote region A as the liquid and region B as the other phase
- If the combination of these two regions is considered an isolated system, then the first law states that the overall change in energy of the system is zero
- The total change in internal energy is given as the sum of the change in internal energy in the two phases and the change in surface energy
- We can express each of the in terms of the natural variables using the Fundamental Thermodynamic Relation ( )
- We note that the temperature of the two regions must be equal () and that any infinitetesimal entropy change by one region ought to be balanced by an equal and opposite infinitetesimal entropy change in the other region ()
- If the volume of one region increases, the other must gets smaller by an equal magnitudes ( )
- This equation relates the pressure difference on either side of an interface with the surface tension and how the area of the liquid changes with volume
Before we go any further, let us look at the implication of this equation
- Surface tension () and the derivative are always positive, so the right side of the equation is always positive
- This means that the difference in pressure must also be positive
- In other words, the pressure inside the liquid is greater than the pressure outside
Spherical Droplets
If the droplet of liquid is spherical, we can use expressions for the surface area and the volume of a sphere from geometry
- Since both the area and the volume are dependent on the radius, we can take differentials of and in terms of
- Substitute it back to the equation will give us the Laplace-Young equation
- One thus arrives at the important conclusion that the smaller the droplet, the greater the internal pressure is relative to the outside
- The difference in pressure decreases to zero as the radius of curvature becomes infinite ( when the surface is flat )
If the system under consideration were a bubble ( a film with an inner and outer surface ) instead of a droplet, then both surfaces will contribute a surface energy and the equation will be modified to \Delta P=\frac{4\gamma}
Condensation and Kelvin Equation
It turns out that the vapour pressure of a liquid is dependent on the curvature of its surface
- Let us first revisit the general expression for the change in Gibbs energy
- Using the relation between the change in area and the change in volume from the derivation of Laplace-Young equation, we can write
- Suppose the volume of the droplet of liquid is changed by at constant temperature and pressure, then
- Recall that the change in Gibbs energy at constant pressure and temperature can also just be written as , comparing these two expression allows us to say that the effective chemical potential is given as
- Assuming ideal gas behaviour, the chemical potential can be written as
- If we set the planar condition to be the standard condition such that ( and )
- The Kelvin equation is usually expressed in exponential form
- The implication of the Kelvin Equation is that small droplets of liquid have a larger vapour pressure than large droplets
We can rationalize the Kelvin Equation with intermolecular bondings
- When the surface is curved, the bonding capacity between molecules and their neighbors diminishes
- Consequently, the likelihood of a molecule breaking free from the liquid and transitioning into the vapor phase rises
Condensation
Consider the process of condensation, such as that of cloud formation
- When the temperature is low, the vapour becomes thermodynamically unstable respective to liquid and we therefore expect it to condense into liquid. The initial step can be imagined as a swarm of molecules congregating into a microscopic droplet
- However, the initial droplet is so small, the Kelvin equation tells us that the vapour pressure of this droplet is immense. The large vapour pressure causes the droplet to evaporate
- In other words, the vapour phase is stabilized because this initial tendency to condense is overcome by a heightened tendency to evaporate, causing the vapour phase to be supersaturated ( The vapour phase is thermodynamically unstable with respect to the liquid phase, but it is more stable than the initial small droplets that need to form before the bulk liquid phase can appear )
In order for condensation to happen, one of two things must happen
- Formation of Spontaneous Nuclear Centers
- When a sufficiently large number of molecules congregate into a droplet so big that it can overcome the enhanced evaporative effect
- The chance of one of these spontaneous nucleation centers forming is quite low
- Presence of Foreign Matter
- These foreign matter can provide surfaces to which molecules can attach to, thereby nucleating the condensation
¶ Surface and Wettability
Interfaces also exist between liquid and solid phases
- Under certain condition, their behaviour is governed by surface tension effects
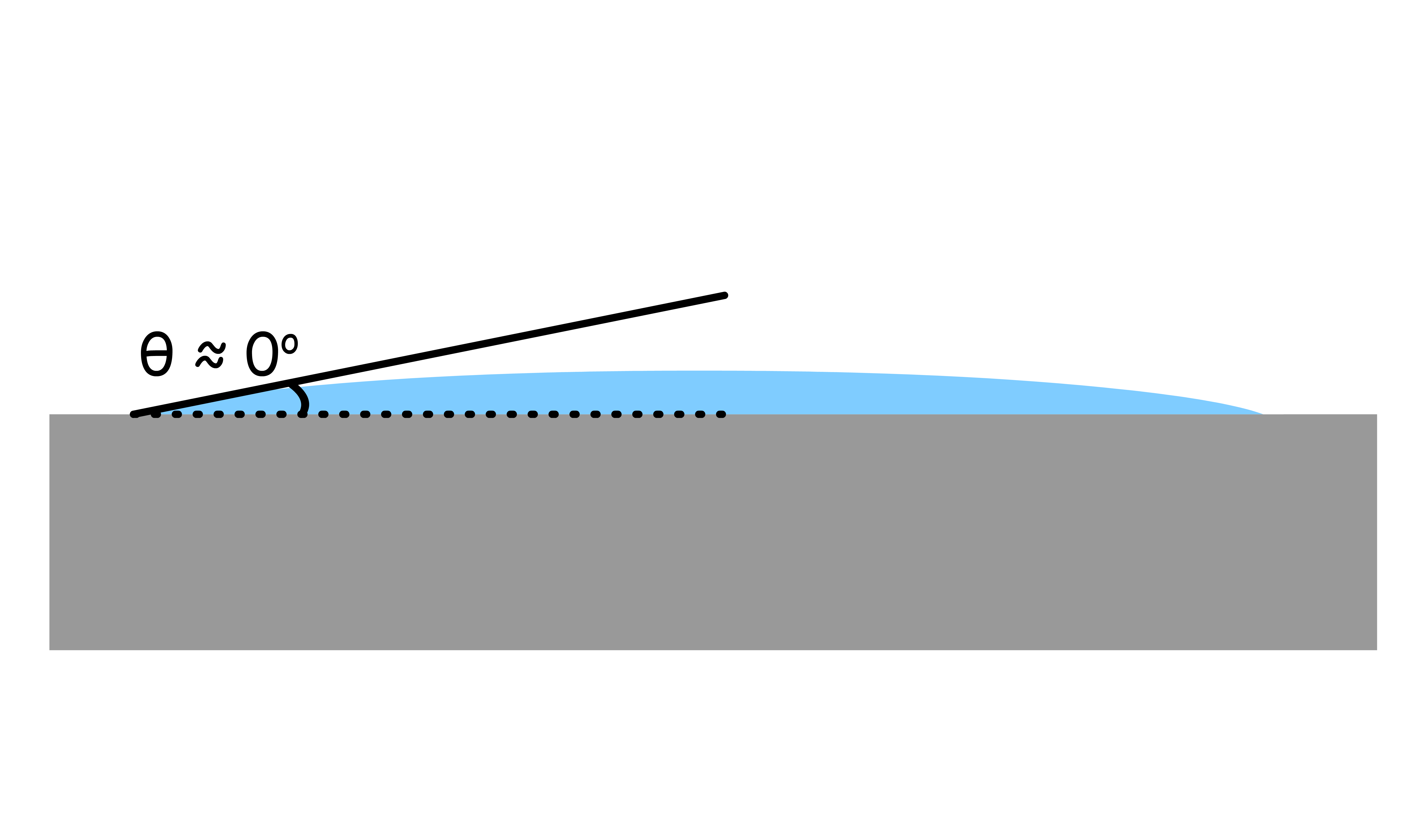
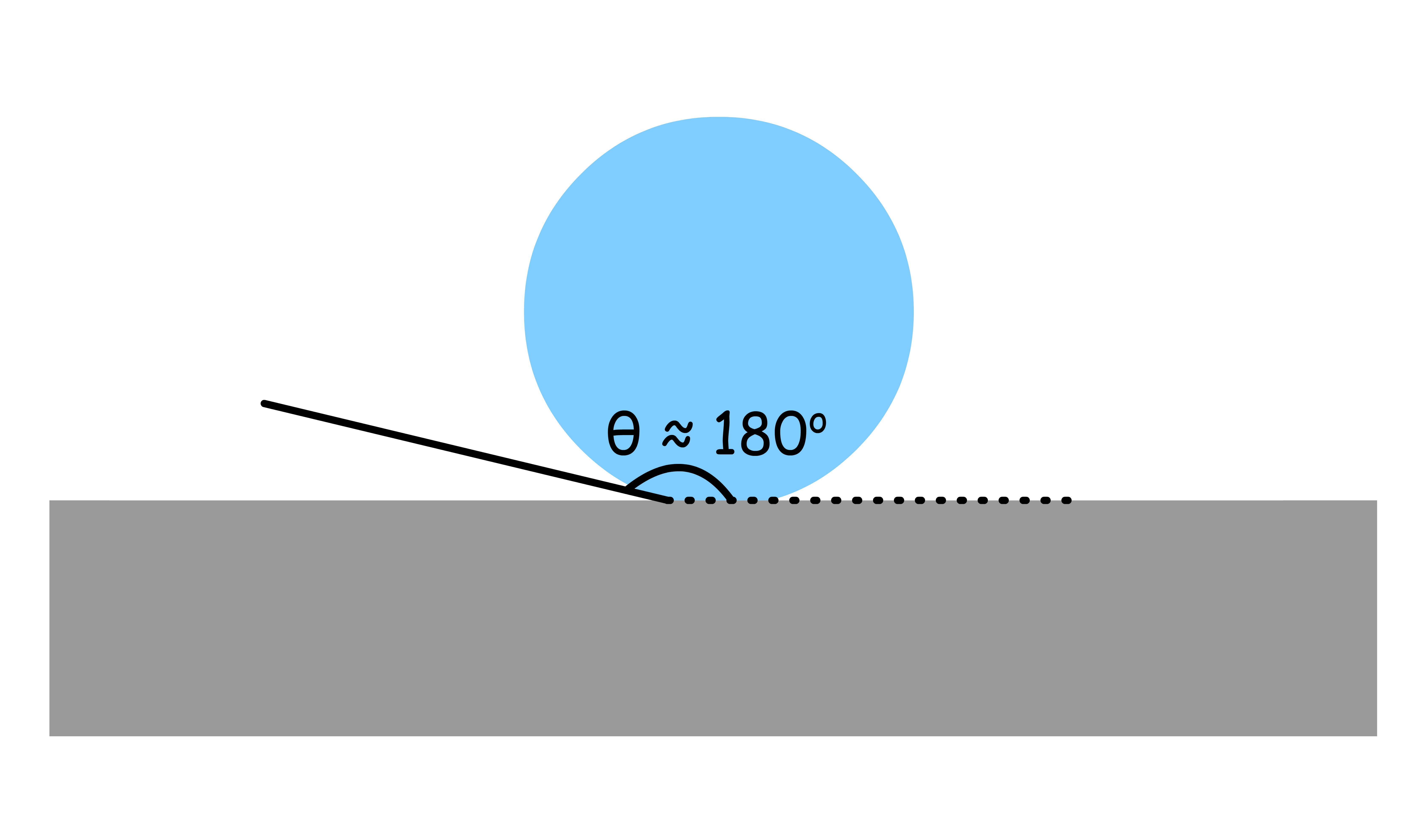
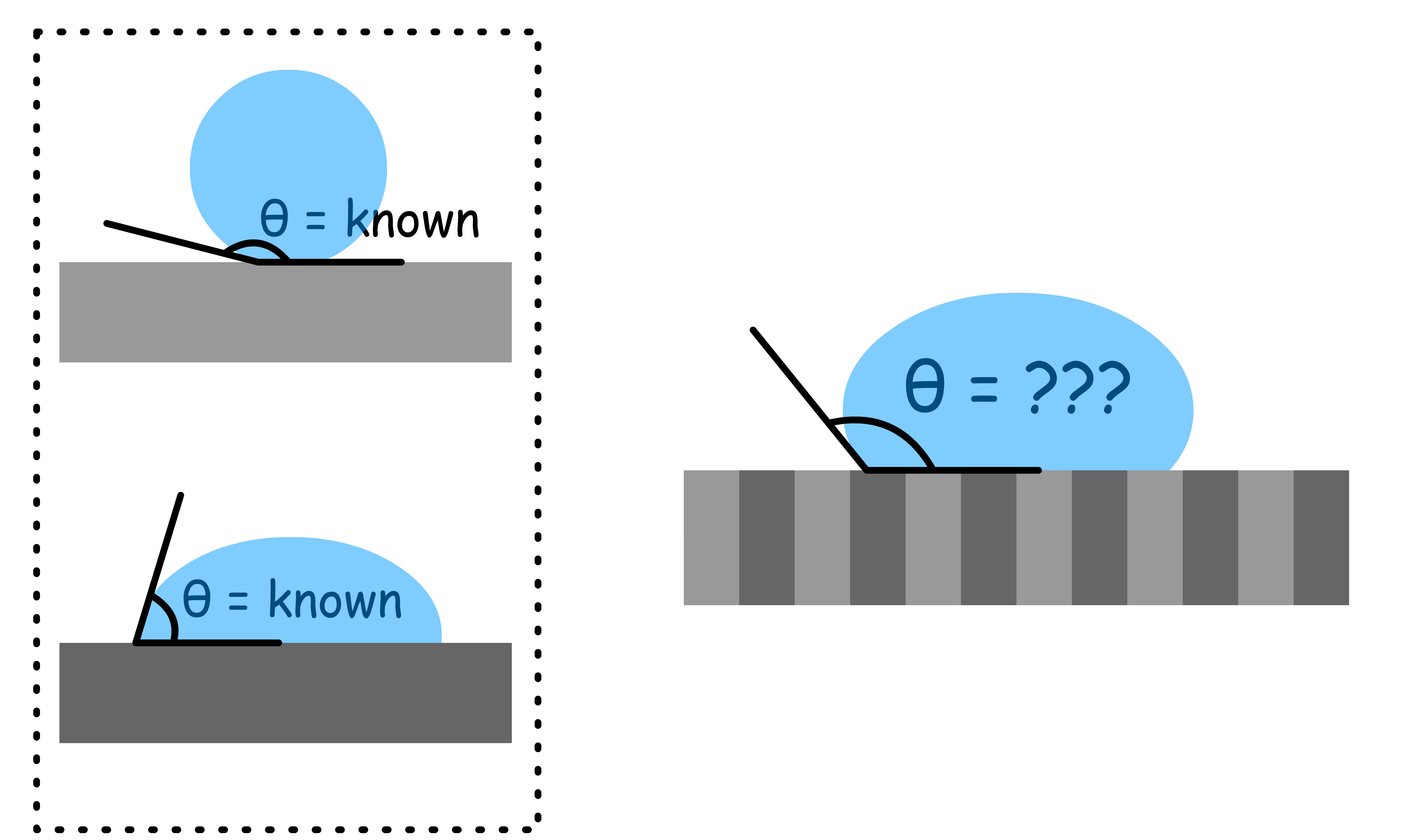
¶ Contact Angle
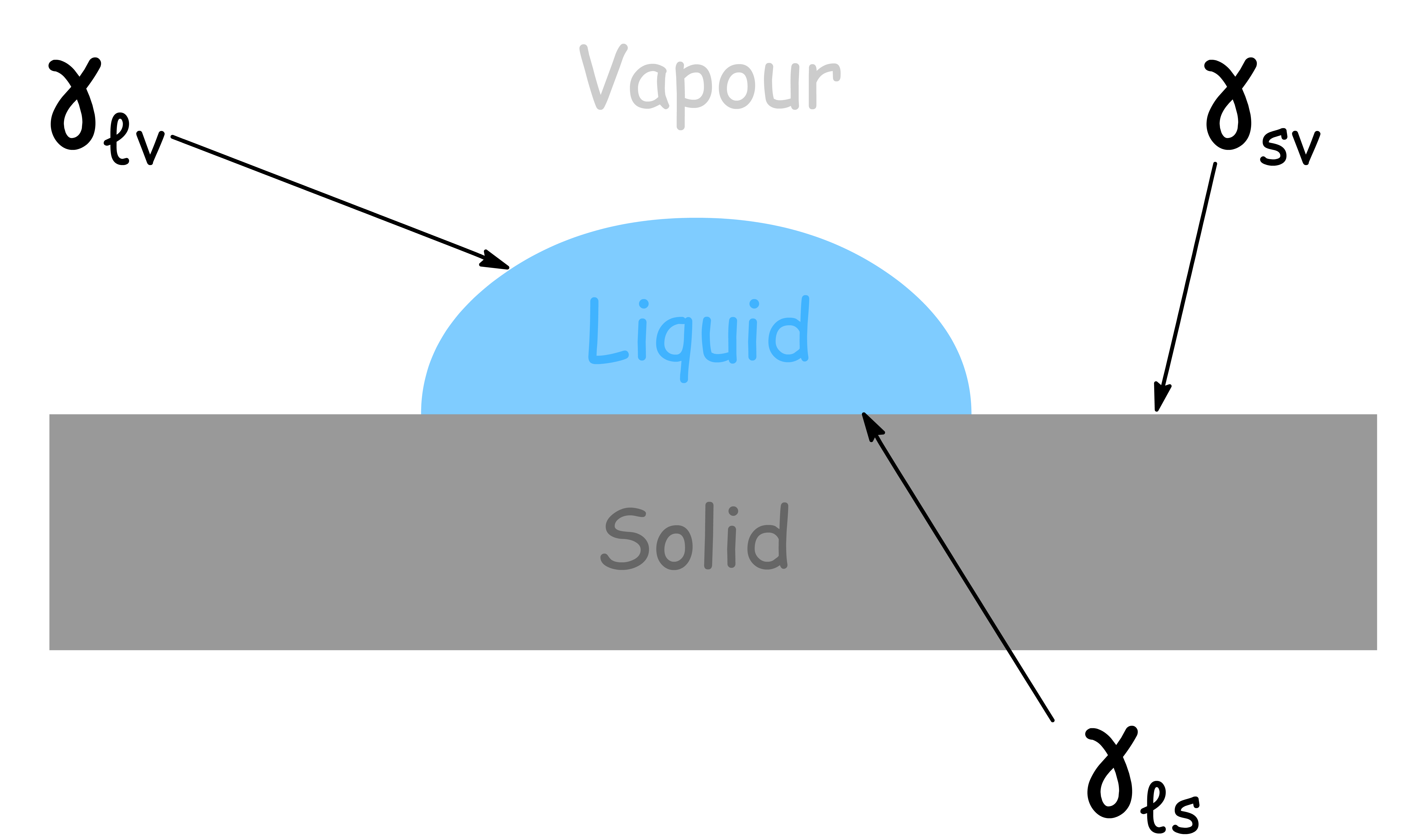
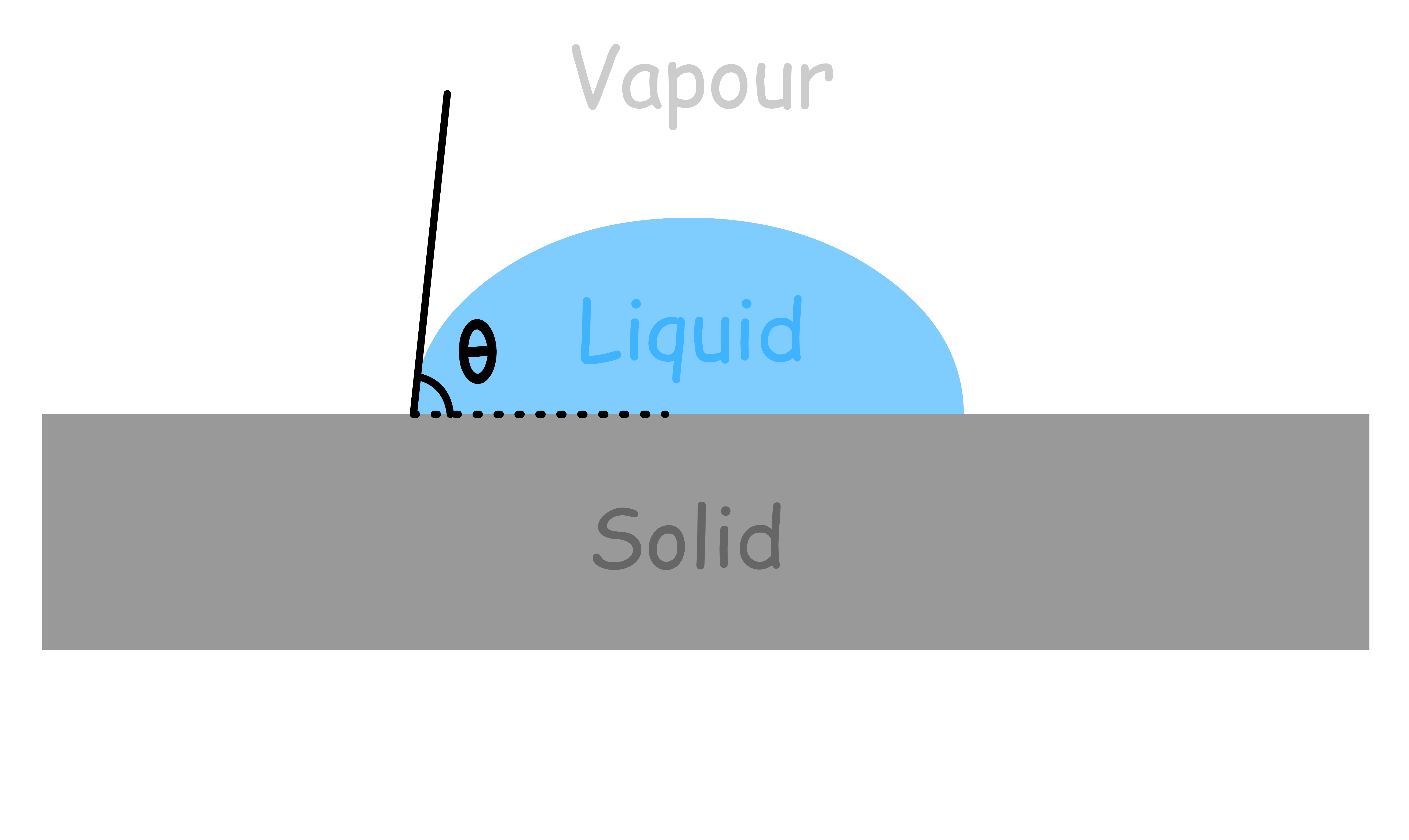
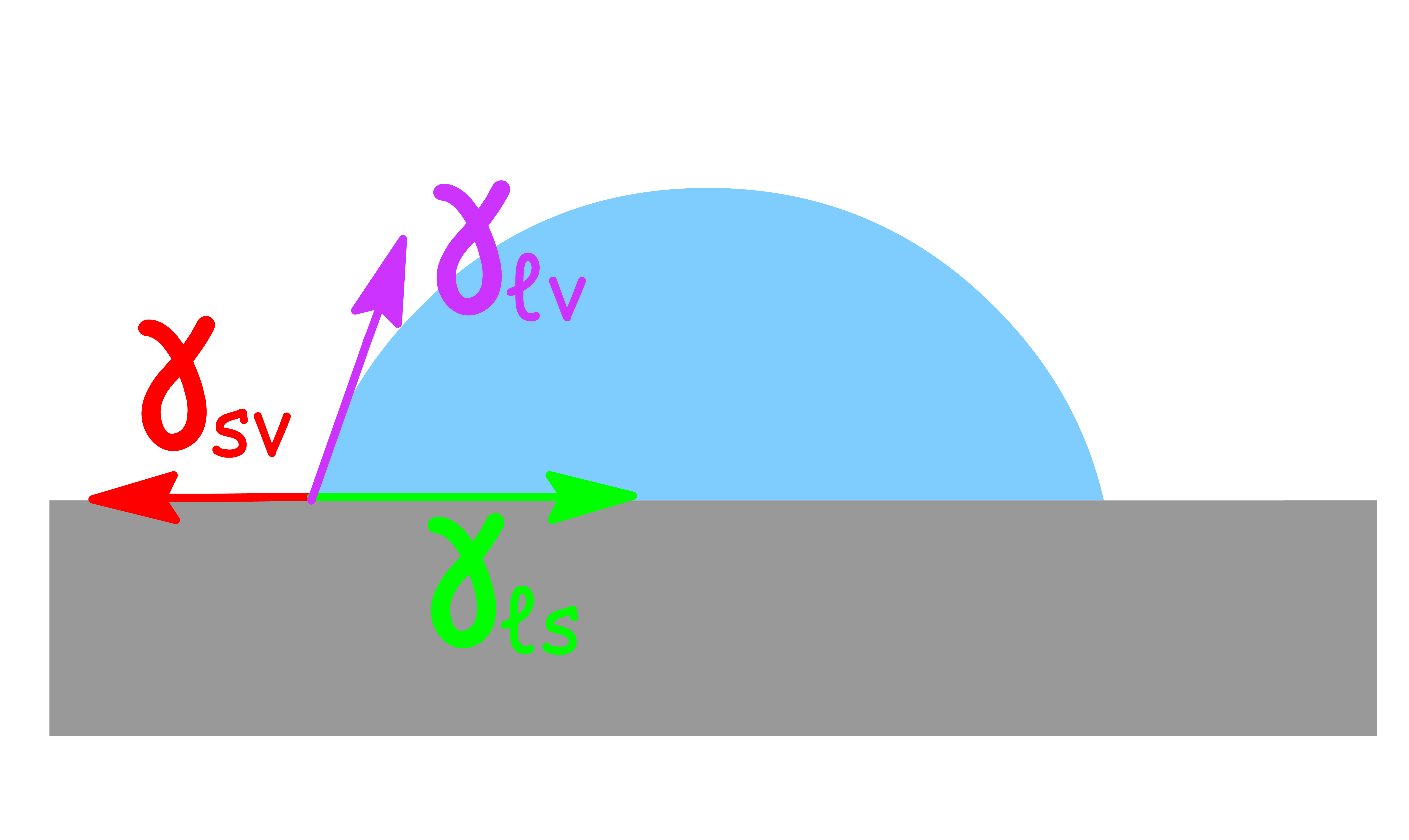
Consider a small droplet of liquid on the surface of a solid
- The way the droplet behaves depends on the surface tension at the liquid-solid interface, the liquid-vapour interface and the solid-vapour interface
- The tangent at the edge of the liquid-solid interface is drawn as a solid line and the angle that this tangent makes with the solid interface is called the contact angle
The contact angle indicates the degree of attraction or repulsion between the fluid and the surface, and how easily the fluid can spread on or adhere to the surface
- When the contact angle is small ( ), the liquid is wetting the solid
- When the contact angle is large ( ), the liquid is not wetting the solid
Young-Dupré Equation
Recall that surface tension is defined as the amount of force that acts per unit length, in an attempt to minimize the interfacial area
- will cause the liquid to spread out and cover the solid phase from the vapor phase as a means to minimize the interfacial area between the solid and vapor phases
- results in the contraction of the liquid to minimize the area of contact between the liquid and solid phases
- causes the liquid to form a compact shape so as to minimize the surface area in contact with the vapor phase
At equilibrium, these force will balance out each other
- Therefore, the behaviour of the droplet is dependent on the relative magnitudes of the three interfacial surface tensions
- If we want a liquid to wet a surface ( ), then should be approximately equal to \gamma_
Spreading Coefficient
The spreading coefficient ( ) is a measure of the tendency of a liquid to spread over a solid surface
- We defined the spreading coefficient as such so that we can rewrite the Young-Dupré Equation in a more simplistic manner
The sign of the spreading coefficient therefore tells us whether the liquid will wet the solid or not
- If the spreading coefficient is positive, the liquid will tend to spread over the surface ( )
- If the spreading coefficient is negative, the liquid will tend to bead up on the surface ( )
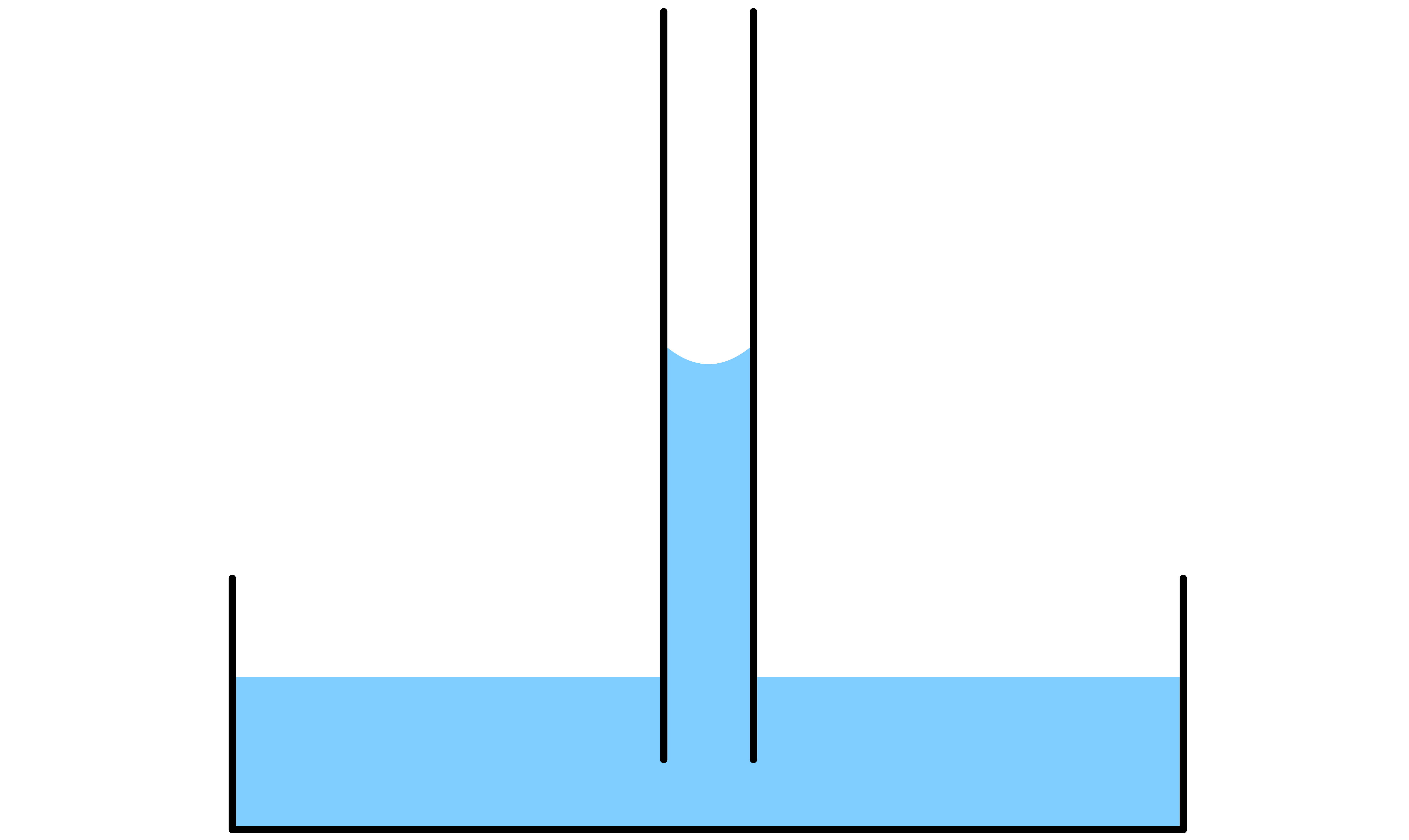
¶ Capiliary Action
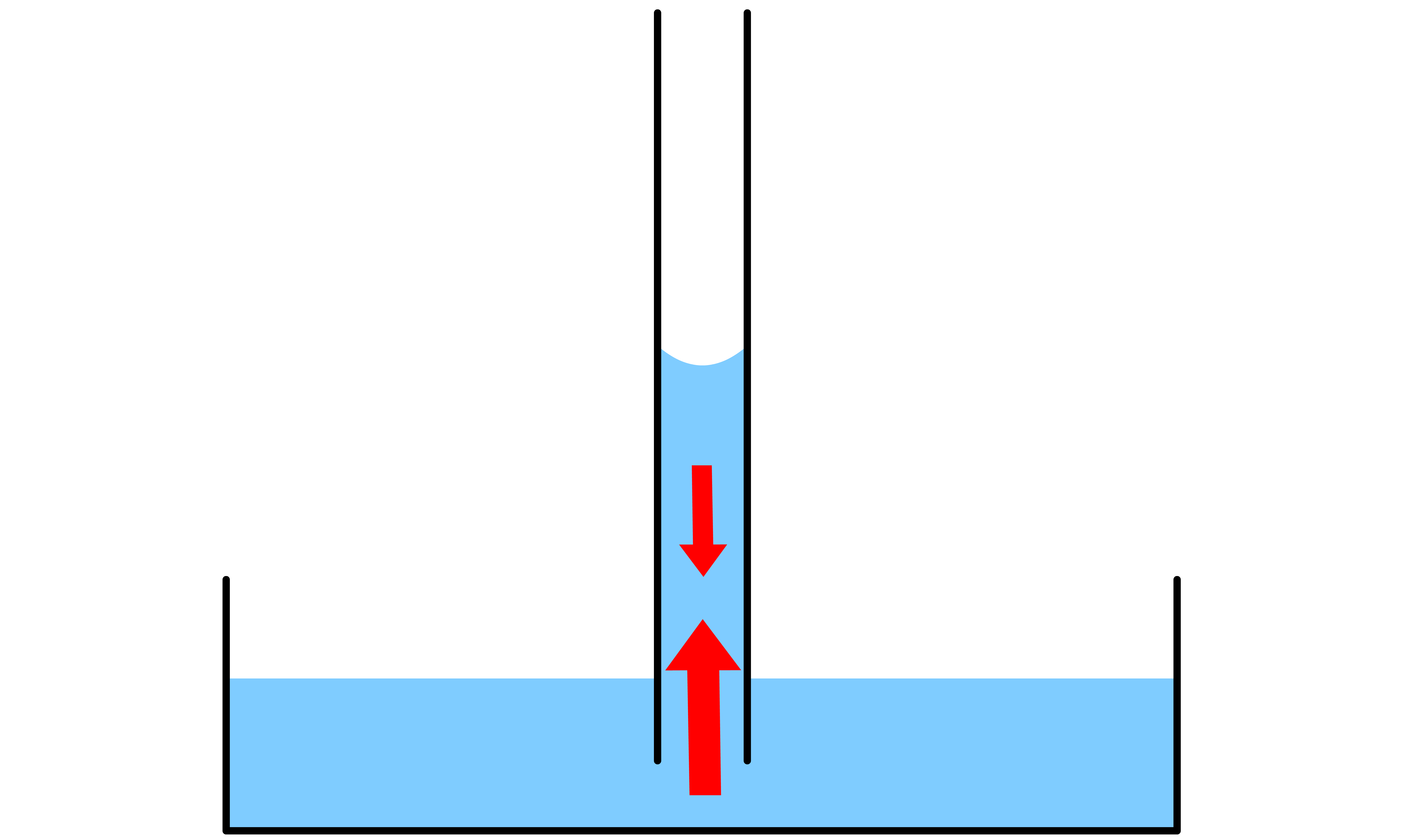
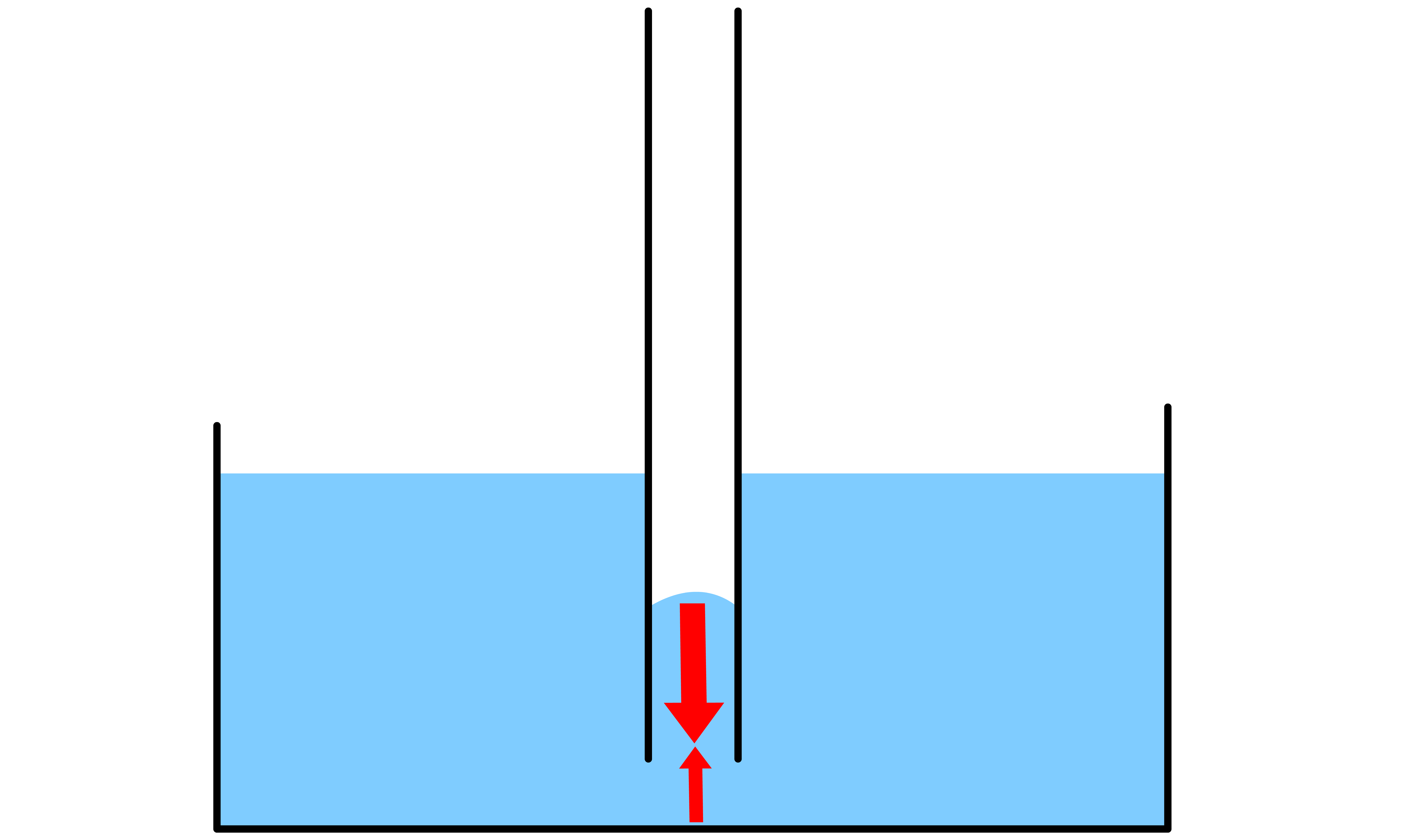
The curvature in a system where a narrow capillary circular tube is dipped into a liquid exhibits properties that are not observed in a large beaker
- The curvature of the liquid inside the tube will lead to pressure difference between this state and the relatively flat surface outside the capillary
Capillary Rise
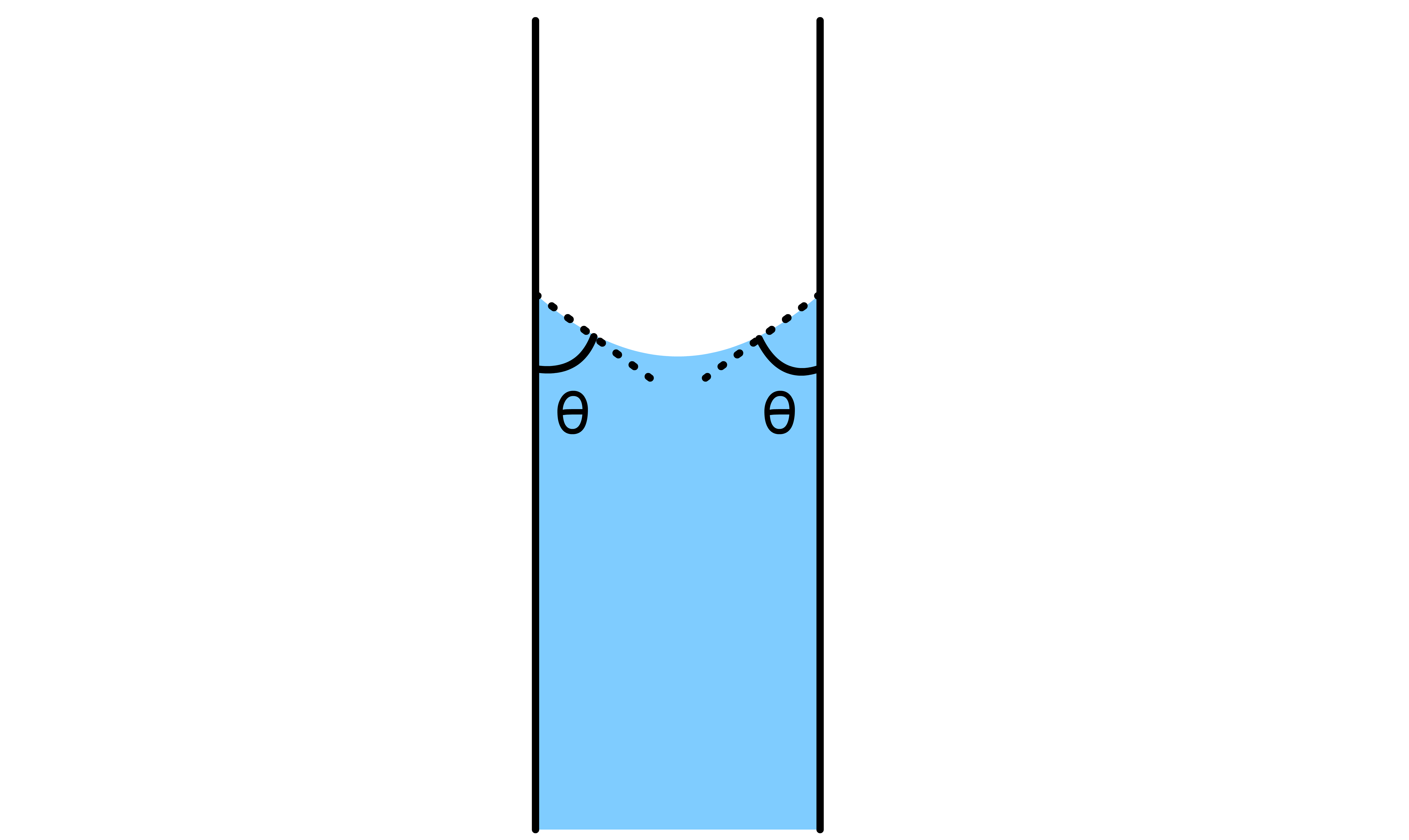
If the liquid in question is able to wet the side of the capillary tube, then the level of the liquid will rise
- By definition, due to the wetting, the contact angle between the liquid and the side of the tube must be ( ). As a result, there will be a concave meniscus
- The Laplace-Young equation states that the pressure difference across the curved liquid interface is directly proportional to the mean curvature of the interface. Since the meniscus is concave, the mean curvature is negative, which means that the pressure at the surface is lower than the pressure in the bulk liquid
Capillary Fall
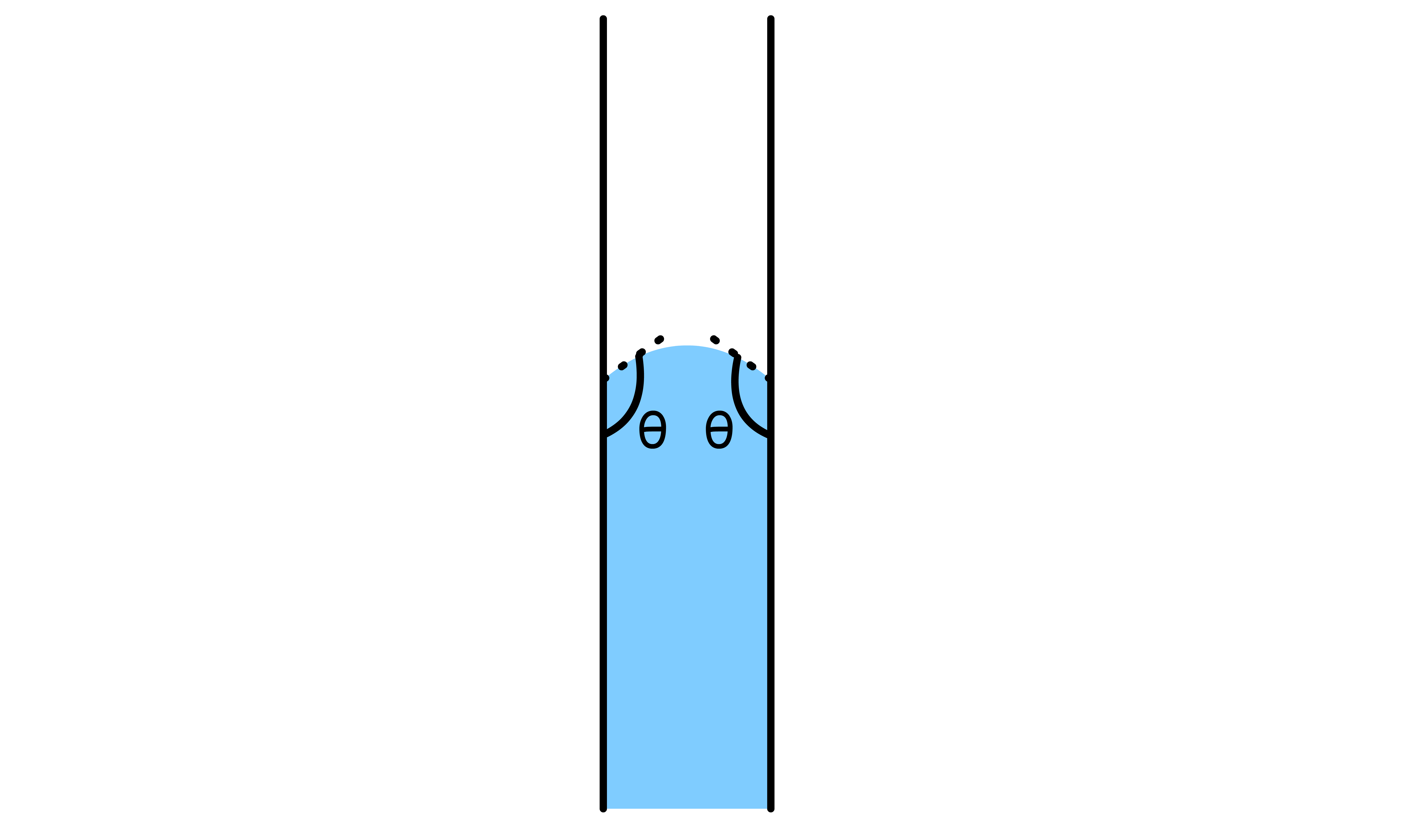
If the liquid in question is not able to wet the side of the capillary tube, then the level of the liquid will fall
- By definition, due to the liquid's inability to wet the tube, the contact angle between the liquid and the side of the tube must be ( ). As a result, there will be a convex meniscus
- The Laplace-Young equation states that the pressure difference across the curved liquid interface is directly proportional to the mean curvature of the interface. Since the meniscus is concvex, the mean curvature is positive, which means that the pressure at the surface is higher than the pressure in the bulk liquid
We can calculate how much the liquid will rise or fall
- The equation describes capillary rise, as well as fall
- In the derivation of the equation, it is assumed that , typically sub-millimetre range. Under these conditions the meniscus has a spherical shape
¶ Capillary Adhesion Forces
Capillary adhesion forces refer to the forces between two surfaces due to the surface tension of a liquid film that is confined between them
- The capillary adhesive force between two substrates can be calculated as such
The nature of capillary force that occurs between two surfaces depends on whether the liquid can wet the surface of the capillary tube
- If the liquid can wet the tube, the contact angle between the liquid and the tube will be between and , resulting in a positive value for . Therefore, the force will be negative in sign and attractive in nature
- If the liquid cannot wet the tube, the contact angle between the liquid and the tube will be between and , resulting in a negative value for . Therefore, the force will be positive in sign and repulsive in nature
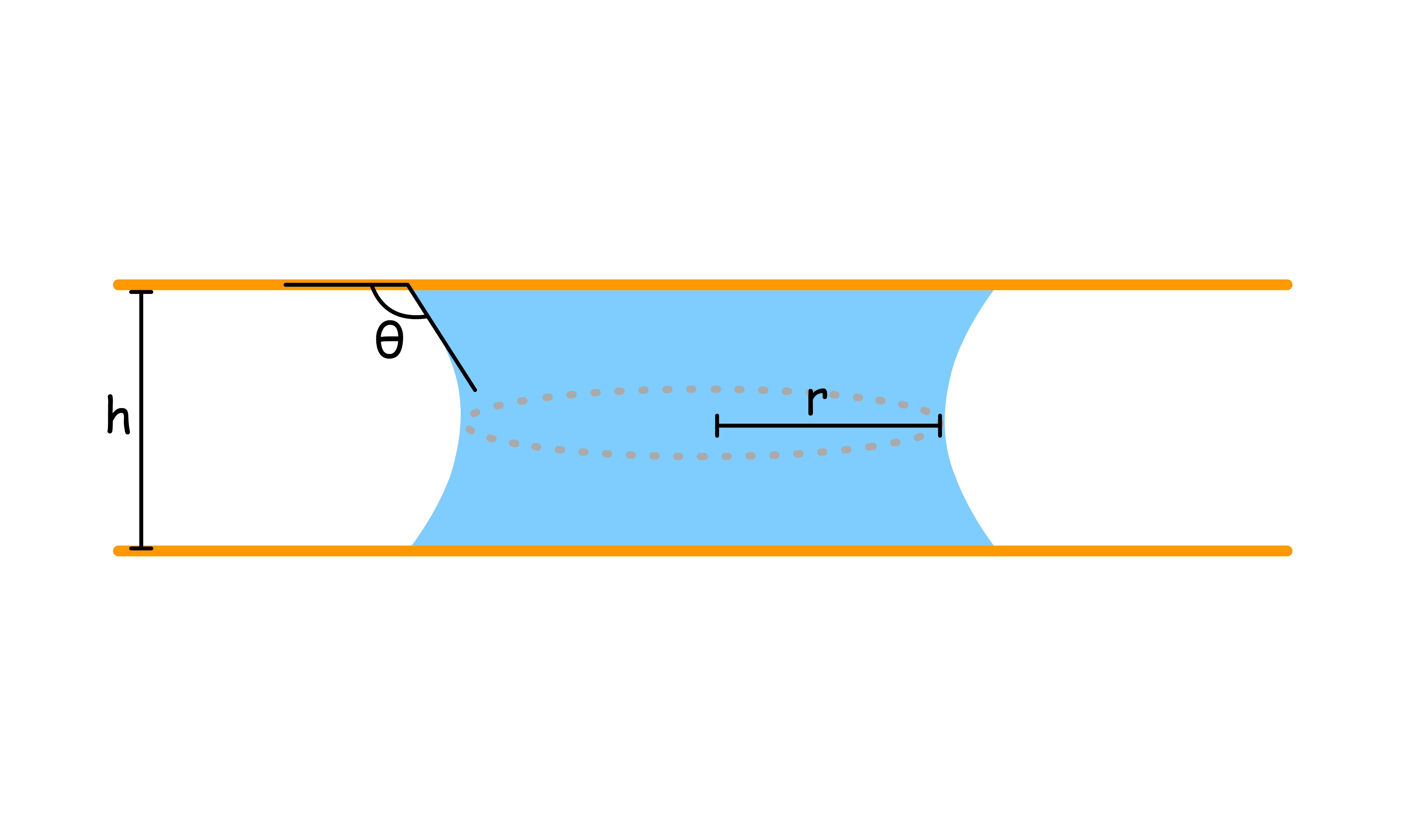
¶ Rough surfaces and Wenzel model
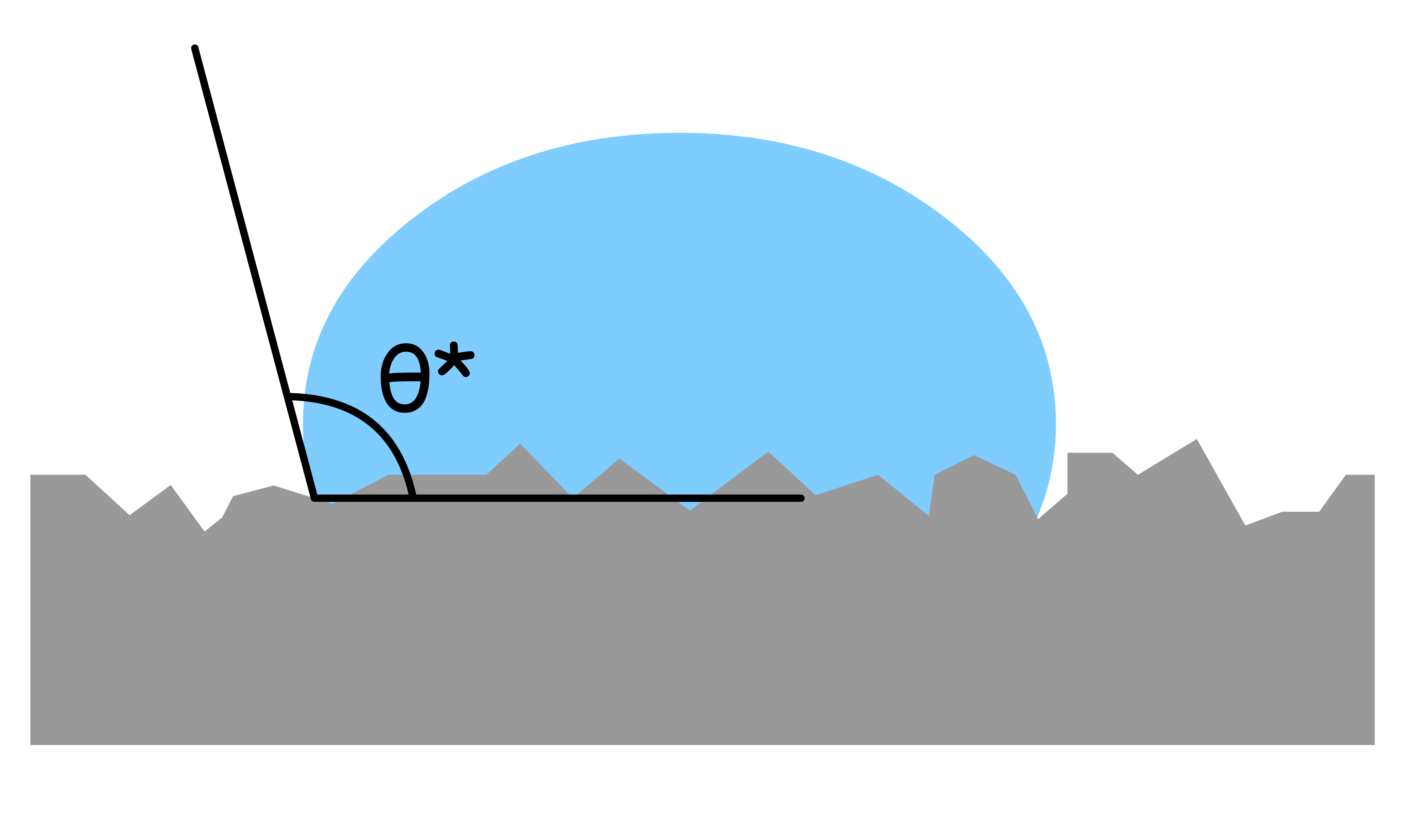
Real-world surfaces are often rough, which causes deviations in the contact angle from the predictions of Young's equation that describes the wettability of atomically smooth surfaces
When a liquid droplet comes into contact with a rough surface, it can penetrate into the small crevices and irregularities of the surface, resulting in an increase in the effective solid-liquid contact area
The increase in contact area enhances the wetting or non-wetting phenomenon between the liquid and solid surface, causing the apparent contact angle, , to deviate from the ideal contact angle,
- For wetting surfaces with contact angles between and , the surface appears to be even more wetting, so
- For non-wetting surfaces with contact angles between and , the surface appears to be even more non-wetting, so
Wenzel Model
The phenomenon of apparent contact angle changes due to surface roughness can be described by the Wenzel model
- The model assumes that the liquid droplet fully fills in the surface irregularities
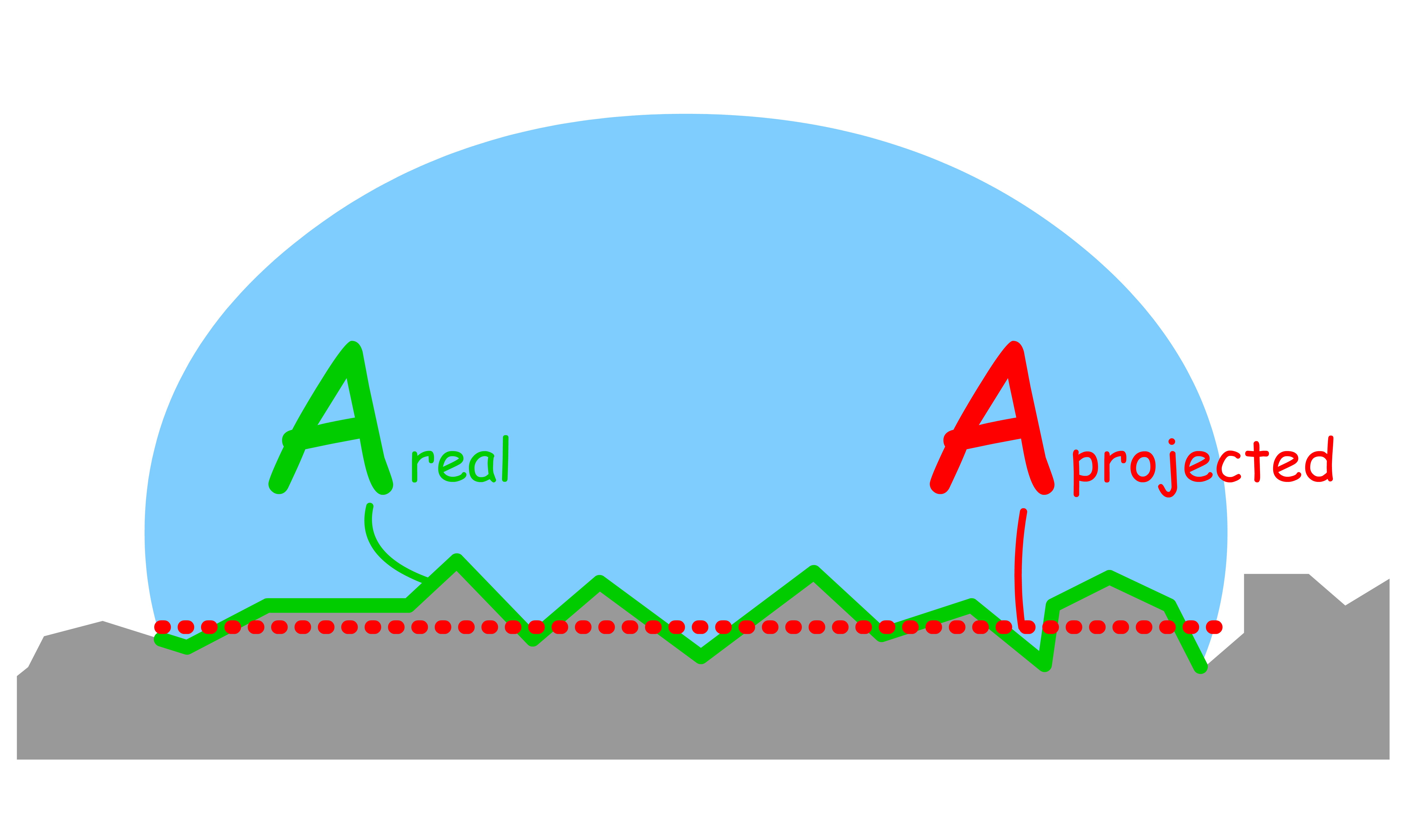
The "roughness" is defined by the ratio of the real surface and the projected surface
- We can relate the apparent contact angle with the ideal contact angle using the concept of roughness
¶ Chemical Heterogeneity and The Cassie-Baxter Model
When we speak of chemical heterogeneity, it means the solid material is composed of different chemical components that have different affinities for the liquid
- This results in a heterogeneous wetting behavior, where different regions of the surface have different wetting properties
- We want to predict the wetting behavior of a heterogeneous system by leveraging the known wetting properties of its individual homogeneous solid components
- The best way to quantify wetting properties is to use contact angles
The Cassie-Baxter Model
The Cassie-Baxter model makes the following assumptions:
- The surface roughness is negligible ( ).
- The surface is composed of two distinct components, each with its own contact angle. The areas of these components on the composite surface are much smaller than the size of the droplet.
The apparent angle, is determined by the average of the contact angles of each solid
The Cassie-Baxter model is also useful for understanding the wetting behavior of hydrophobic surfaces with roughness
- One of the main features of such surfaces is that vapor can become trapped underneath the liquid, creating a mixed surface of solid and vapor
- When the surface roughness is taken into account, the Cassie-Baxter model predicts that the contact angle between the liquid and the surface will depend on the fraction of the surface that is covered by vapor
- As the roughness of the surface increases, the amount of trapped vapor also increases, which in turn reduces the area of solid-liquid contact and increases the contact angle
¶ Adsorption
¶ Surface Excess
Some solutes may not be uniformly distributed throughout a solution, as they can either accumulate at or avoid the interface
- In order to discuss this phenomenon in a quantitative manner, the concept of surface excess is introduced
Surface excess is a quantitative measure of the amount of a substance that accumulates at the interface, in excess of what would be expected based on its bulk concentration
- For a solute that accumulates at the surface, the surface excess is positive
- For a solute that avoids the surface, the surface excess is negative
We can write something similar for Gibbs energy as well
- Since the surface has no volume, we can express the differential of the surface Gibbs Energy as such at constant temperature
- The Euler's theorem allow us to write down , so its total differential is
- Equating both expressions of gives us the Gibbs-Duhem equation
- We shall define the surface excess per unit area as , the surface concentration
This equation can be interpreted as follows
- If adding more of solute (raising its chemical potential) decreases the surface tension, then is positive and solute will accumulate at the interface
- If adding more of solute (raising its chemical potential) increases the surface tension, then is negative and solute will avoid the interface
A substance that significantly lowers the surface tension and accumulates at the surface is called a surfactant
Dependence of Surface Tension on Surfactant Concentration
Now consider a simplified model of the interface where the only non-zero is the surfactant's
- For ideal solutions, the chemical potential of the solute can be written in terms of the concentration of the solute , substituting it back to the isotherm gives us
- If the surfactant accumulates at the interface, its surface excess is positive and will be negative. That is, the surface tension decreases when a solute accumulates at a surface
¶ Langmuir Isotherm
The Langmuir isotherm is a model used to describe the adsorption of molecules onto a surface at a constant temperature
- It is characterized by a dimensionless parameter, , which represents the fraction of available surface sites that are occupied by adsorbate molecules
Langmuir isotherm is the simplest model as it is based on several key assumptions that simplify the adsorption process
1. Maximum of monolayer coverage
- The Langmuir isotherm assumes that only a monolayer of adsorbate molecules can form on the surface
- This means that there is a maximum limit to the number of adsorbate molecules that can occupy the surface at any given time.
2. All sites on the surface are equivalent
- The Langmuir isotherm assumes that all sites on the surface are equivalent and have the same energy
- This means that any adsorbate molecule can occupy any site on the surface with the same probability
3. A molecule can be adsorbed only at a vacant site
- The Langmuir isotherm assumes that adsorption occurs only when there is a vacant site on the surface
- This means that an adsorbate molecule cannot displace another adsorbate molecule that is already adsorbed on the surface
- Moreover, molecules cannot be adsorbed onto another adsorbed molecule
4. No lateral interactions between adsorbed molecules
- The Langmuir isotherm assumes that there are no lateral interactions between adsorbed molecules
- This means that the adsorbate molecules do not interact with each other and do not affect the adsorption of other molecules on the surface
The Langmuir isotherm equation
The Langmuir isotherm equation aims to use this simplistic model to relate to the partial pressure of the adsorbate in the gas phase
- The rate of change of the "concentration" of adsorbant on an interface is given by
- At equilibrium, the rate of change of the "concentration" of adsorbant will be zero
- We shall define the ratio of rate constants as the Langmuir adsorption constant , which is a measure of the affinity of the adsorbate for the surface
- has units , while has units , so has units of \text{Pa}^
A similar approach can be taken for species in solution
- We use activities or concentration instead of partial pressure
¶ Free Energy of Adsorption
Recall that we can relate the change in Gibbs energy at constant temperature and pressure to the dimensionless equilibrium constant
- We can do the same here
- We multiply the Langmuir adsorption constant by the standard pressure to get a dimensionless quantity while keeping the same numerical value
¶ Isosteric Enthalpy of Adsorption
Isosteric refers to a constant coverage,
We can use the Gibbs-Helmholtz equation to derive the following
- Alternatively, we can write
The temperature dependence of can be used to determine the enthalpy of adsorption of a given covergae
¶ BET isotherm
The BET (Brunauer-Emmett-Teller) isotherm was developed to address the limitations of the Langmuir model, which assumes that adsorption occurs on a homogeneous surface with a fixed number of adsorption sites
- The BET model, on the other hand, takes into account the fact that the initial adsorbed layer can act as a substrate for further adsorption
- In other words, adsorption is “open ended” as it is not limited to one monolayer
- Therefore, instead of using the Langmuir parameter , which ranges from to to represent the fractional coverage of the surface, the BET model uses the parameter , which ranges from to , to represent the ratio of the volume of gas adsorbed to the monolayer capacity of the surface
The most widely used isotherm dealing with multilayer adsorption is called the BET isotherm
- When formation of monolayer occurs easily
- is a constant which is large when the enthalpy of adsorption from a monolayer is large is large compared with the enthalpy of condensation
¶ The Rate of Adsorption and Desorption
Adsorptions and desorptions are activated processes, in the sense that they have an activation energy and follow Arrhenius behaviour
- We shall now delve into the origin of the activation energy in these processes
The Intermediate States
The potential energy of a molecule varies with its distance from the substrate surface
- Initially, when the molecule is approaching the surface, it becomes physisorbed. This causes its potential energy to drop slightly and it will be in an intermediate state
- In order to be chemisorbed, the molecule will dissociate into fragments. The potential energy will increase slightly due to the dissociation before dropping rapidly as the adsorbant-substrate bond forms
- Even if the molecule does not fragment, there is likely to be an initial increase of potential energy as the molecule approaches the surface and the bonds adjust
- The higher the activation energy, the lower will be
Transport of adsorbate to the surface
Transport of adsorbate to the surface is an essential step in the adsorption process
- The adsorbate must be transported from the bulk phase, whether it be a solution or gas, to the surface of the adsorbent material
- There are different mechanisms by which this transport can occur, including solution processes and porous materials
In solution processes, the adsorbate is transported through the solvent to the surface of the adsorbent material
- The rate of diffusion in the solvent is typically much slower than in the gas phase. The typical diffusion coefficient in a solvent is around , while in the gas phase it is around 10^{-5} m^{2} s^
- Fick’s 1st law tells us that the rate of transport in the solution phase can be up to 10^4 times slower than in the gas phase
- The characteristic diffusion time for a distance x is given by . To diffuse 1 cm, it would take about 5 seconds in the gas phase and about 14 hours in the solution phase
In porous materials, the transport of the adsorbate to the surface is affected by the pore structure of the material
- The surface area of the material is increased in porous materials, but the effective diffusion rate is decreased due to the tortuous path that the adsorbate must take to reach the surface
- In general, the transport of the adsorbate to the surface in porous materials is slower than in non-porous materials, but the increased surface area can lead to higher adsorption capacities