Classical physics allows us to do two things
- Predict a precise trajectory for particles, with precisely specified locations and momenta at each instant
- It allows the translational, rotational, and vibrational modes of motion to be excited to any energy simply by controlling the forces that are applied
- These classical physics conclusions agree with our macroscopic everyday experiences, but they do not extend to the microscopic world
Quantum mechanics encompasses two key ideas
- Everything has properties of particles and a wave
- Many continuous properties are quantized
- We shall see later how these two concepts are intrinsically related
Historically, quantum mechanics developed independently by different scientists
- The first approach was matrix mechanics, developed by Heisenberg, Born and Jordan. A different yet equivalent approach, wave mechanics, was later developed by Erwin Schrödinger
- The two approaches were later unified in the state space formalism by Paul Dirac
¶ Wave-Particle Duality
The central idea in quantum mechanics is the idea of wave particle duality
- This is the idea that distinguishes it from classical physics
In classical physics, all macroscopic phenomena can be reduced to the interactions of two classical elementary objects: Particles and waves
- Particles obey the laws of Newtownian mechanics, while wave fields obey Maxwell's equations
- Every elementary object is either a particle, or a wavefield in the eyes of classical physics and the two are mutually exclusive with distinctive features
In quantum mechanics, we shall see the boundaries errode between what we consider as particle and wave
- We no longer see particle and waves as two classes of objects, but rather two distinct modes of behavior that is shared by all classes of objects
- Everything can behave like a particle and like a wave
- The question of whether something is a particle or a wave has lost its meaning, because seeing particles and waves as distinct objects is not possible in quantum mechanics
¶ The Nature of Light
In classical physics, we treat light as waves as it displays a lot of wave-like properties that particles cannot exhibit
- However, there also exists evidence that shows that light have particle-like properties
Planck proposed that the energy of light is limited to discrete values and cannot be varied arbitrarily
- He supposed that energy of light is not arbitrary, but proportional to their frequency,
- To convert the relation to an equality, we shall include a proportionality constant, , which is now called the Planck constant
- It is often more natural to talk in terms of angular frequency, , than frequency, , so we can also write the equation as
- We shall therefore define as another constant, , which is called the reduced-Planck constant
-
As we venture into the realm of quantum chemistry, we will keep bumping into the Planck's constant and reduced-Planck's constant
-
We can therefore consider light as a particle that carries a discreet amount of energy, which is predicted by the equation above
-
We call these light particles as photons
Light shows both the properties of waves and particles
- Light can be treated as a stream of individual particles, each of which carries a certain amount of energy whose value is determined by its wavelength
¶ The De Broglie Wavelength
De Broglie hypothesized that if a wave like light can have properties of particles, then particles should also have wave properties
- We can rationalize De Broglie's hypothesis by equating the expression for energy from special relativity and from quantum theory
- Since De Broglie believed particles and waves have the same traits, he hypothesized that the energy from special relativity and quantum mechanics are equal
- From classical physics, we know that , we can therefore substitute for frequency :
- By canelling the speed of light constant from both sides and acknowledging that it is a velocity, and that mass times velocity is the magnitude of the linear momentum, we get:
- Making the wavelength the subject of this expression, we arrive at the De Broglie's equation:
The equation states that the wavelength of a particle is inversely proportional to its momentum, and the proportionality constant is h, the Planck's constant
- The equation implies that a particle with mass has wave-like behaviour
Since the De Broglie's wavelength of particle is inversely proportional to the mass of said particle, the wavelength becomes shorter as the mass of the object becomes larger
- Sub-atomic particles have a small enough mass that their wave behaviour dominates
- The wavelength of macroscopic objects are too short relative to the object itself to have any significant effects
The equation also implies that light has momentum
- Photons carry momentum, showing further that they behave like particles
¶ The Postulates of Time-Independent Quantum Mechanics
Postulates are not things that are proven to be true, but are taken as given to be true
- Postulates are judged on whether or not they are true by the validity of their predictions
Quantum mechanics is founded on a set of postulates that are proven to be a good description of reality
- We will use these postulates to derive all of quantum mechanics
- These postulates are as fundamental to quantum mechanics as Newton's law of motions are to classical mechanics
Formally, the set of postulates include one that dictates how quantum systems behave overtime
- However, we will leave that discussion later until we have familiarized ourselves with the time-independent version of quantum mechanics
¶ The State of a Particle
In physics, the state of a particle is a set of time-dependent variables.
- When accurately specified, not only all possible information about the system at that time can be obtained from the state, but the entire time evolution of the state can be determined from the dynamical laws governing the system
In quantum mechanics, it is postulated that the state of a particle is represented by a ket vector in an infinite dimensional Hilbert space over a complex field
- Hilbert space is a linear vector space equipped with an inner product and is complete
- in quantum mechanics, the Hilbert space is also a function space, so ket vectors can also be manifested as functions
The vector that is representing the state is called the state vector
- the state vector contains all dynamical information that can be known about the state
¶ Observables and Operators
When studying the state of a system, one typically makes various measurements of its properties.
- Each dynamical variable is called an observable
In quantum mechanics, it is postulated that each observable is assigned a linear Hermitian operator
- Moreover, the only result of a precise measurement of the observable is one of the eigenvalues of the corresponding Hermitian operator.
We have stated that the measurements are related to eigenvalues, the next thing we should be asking is what the eigenvector equation should be
- It should go without saying that if an eigenvalue exists, there must also be at least one associated eigenket
- Most operators have more than one eigenvalue, so the result of the measurement will depend entirely on what the vector is
The set of eigenvectors of an operator can be made to form an orthonormal set of eigenbasis, so every observable in quantum mechanics has its set of orthonormal eigenbasis
- This means that the state vector can be represented in the observables' eigenbasis through the inner product between the state vector and each eigenbasis
The Hermitian operators of observables can be constructed in a way analogous to that of classical mechanics
- In classical mechanics, the two most fundamental dynamical variables are position and linear momentum. All other dynamical variables are functions of position and linear momentum and so they can be written in terms of those two fundamental dynamical variables
- We take a similar approach in quantum mechanics, we postulate that all the operators of observables can be constructed by simply replacing the position and linear momentum in their classical expression by the position operator and linear momentum operator respectively
- and are the spatial coordinate and the linear momentum respectively and their operator will be derived in later sections
¶ The Probabilistic Nature of Quantum Mechanics
We have established that the state vector contains all information that can be acquired from the state and that operators extract the values of measurements
- It is therefore unsurprising that the values of the observable of a state are extracted by using the corresponding Hermitian operator on the state vector:
- This would be the end of the story if the state vector was an eigenvector of the observable and the value of the measurement will simply be the corresponding eigenvalue
Unfortunately, more often than not, the state vector is not the eigenvector of an observable. Since the previous postulate restricts the value of the measurement to be a single eigenvalue, the question then is which one.
- If this is the case, we need to represent the state vector in that observable's eigenbasis:
- The inner product between the eigenbasis vector and the state vector is the component of that basis vector and it can be interpreted as the "similarity" between the state vector and that particular basis vector
- In quantum mechanics, it is postulated that the probability of an eigenvalue being the value of the measurement is directly proportional to the component of the corresponding eigenbasis:
- Since we are working in a complex vector space, the component can be a complex number, which does not make sense in the language of probability. To get around this, we multiply the inner product by its complex conjugate.
- In fact, if the state vector is normalized, the above relation becomes an equality
Furthermore, it is postulated that the measurement of the observable changes the state vector, which is usually the linear combination of the set of eigenbasis vectors, into the eigenket corresponding to the eigenvalue obtained in the measurement
- This phenomenom is called the collapse of the state vector
- The measurement here is assumed to be an ideal one, which in classical physics, would not have affected the system in any way. However, in quantum mechanics, the very act of measuring an observable will force the system into an eigenstate of that observable
The probabilistic nature of quantum mechanics allows us to employ certain math from probability theory
- In probability theory, the expected value is the generalization of the weighted average. In quantum mechanics, we refer to the expected value of measurements as an expectation value denoted as
- Using the definition of expected value, the expectation value of an operator is defined as such for normalized state vectors
- Expanding this expression gives us:
- We can then rearrange the expression and make use of the properties of eigenvectors and eigenvalues.
- The sum of the outer product of the eigenvectors will just give us the identity operator
- This is the expression for the expectation of an observable in quantum mechanics.
¶ Wavefunctions
We have introduced the state vector and the fact that the state vector can be represented in the eigenbasis of different observables.
- One basis that we are most interested in is the position basis
- The position operators form a continuous spectrum of eigenbases, so we will treat the state vector as a function:
- Here, represents the position basis
- This representation is so common and important, that the implicit choice of basis for the state vector is the position basis. Moreover, we refer to this function as the wavefunction
In chemistry, we prefer to deal with wavefunctions instead of state vectors whenever possible
- However, it is important to bear in mind that the wavefunction is simply a representation of the state vector.
¶ Born interpretetation of the Wavefunction
Since the wavefunction is just the state vector in the position eigenbasis, it should be obvious that we can easily extract information about the position of the particle from the wavefunction
- For a normalized state vector, the probability of the measurement being a certain eigenvalue is given by:
- In terms of the wavefunction, the expression can be rewritten as:
- However, since the position eigenvectors form a continuous eigenbasis, it does not make sense to talk about discrete probability. Instead, we describe the probability using the probability density:
- This is called the Born rule
Born showed that the probability density function, , of a particle is given by the square modulus of the wavefunction.
- In other words, the probability can be evaluated over a definite region, not a specific point
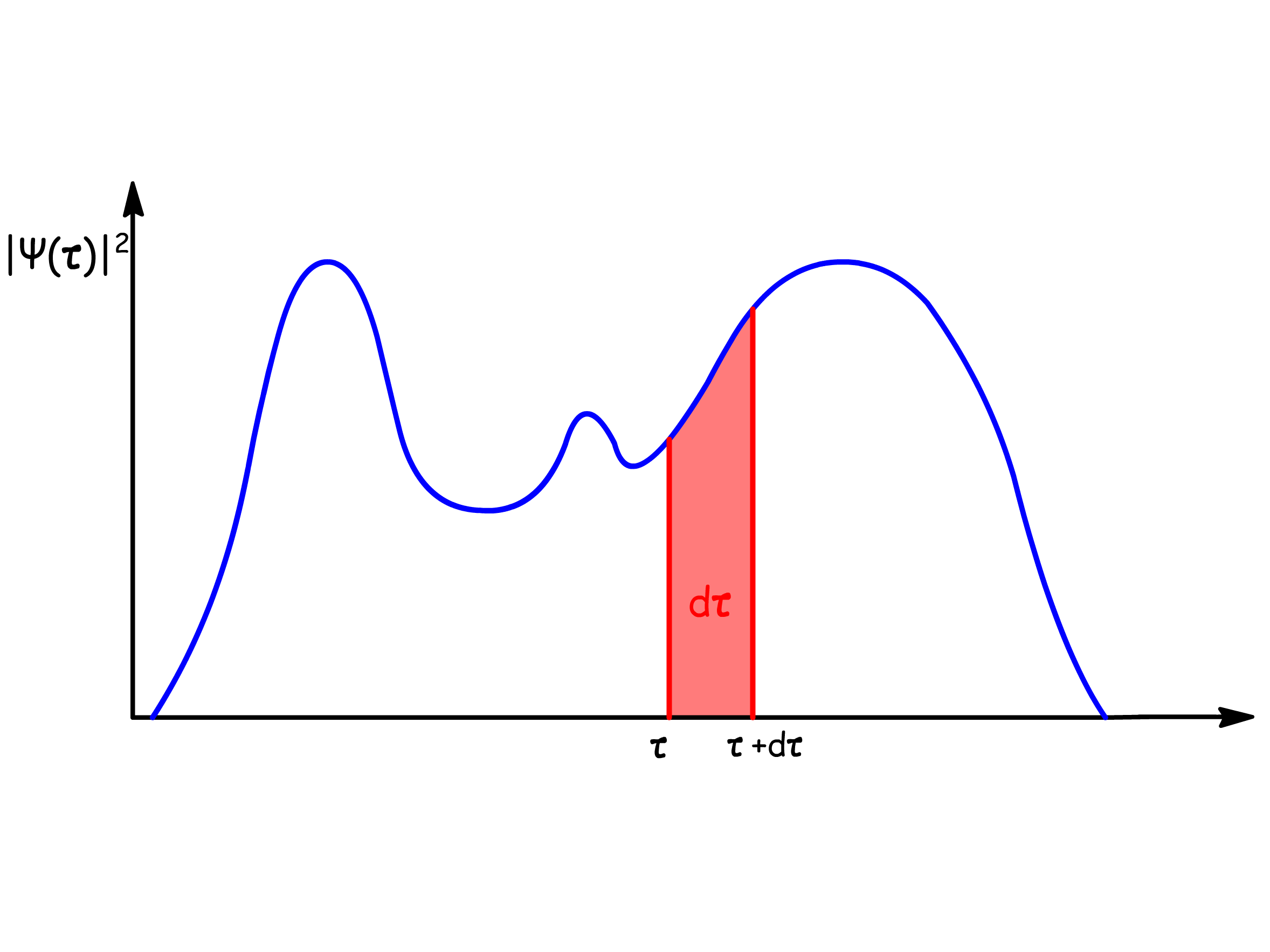
- is the infinitesimal variable of integration covering the dimensional space of interest
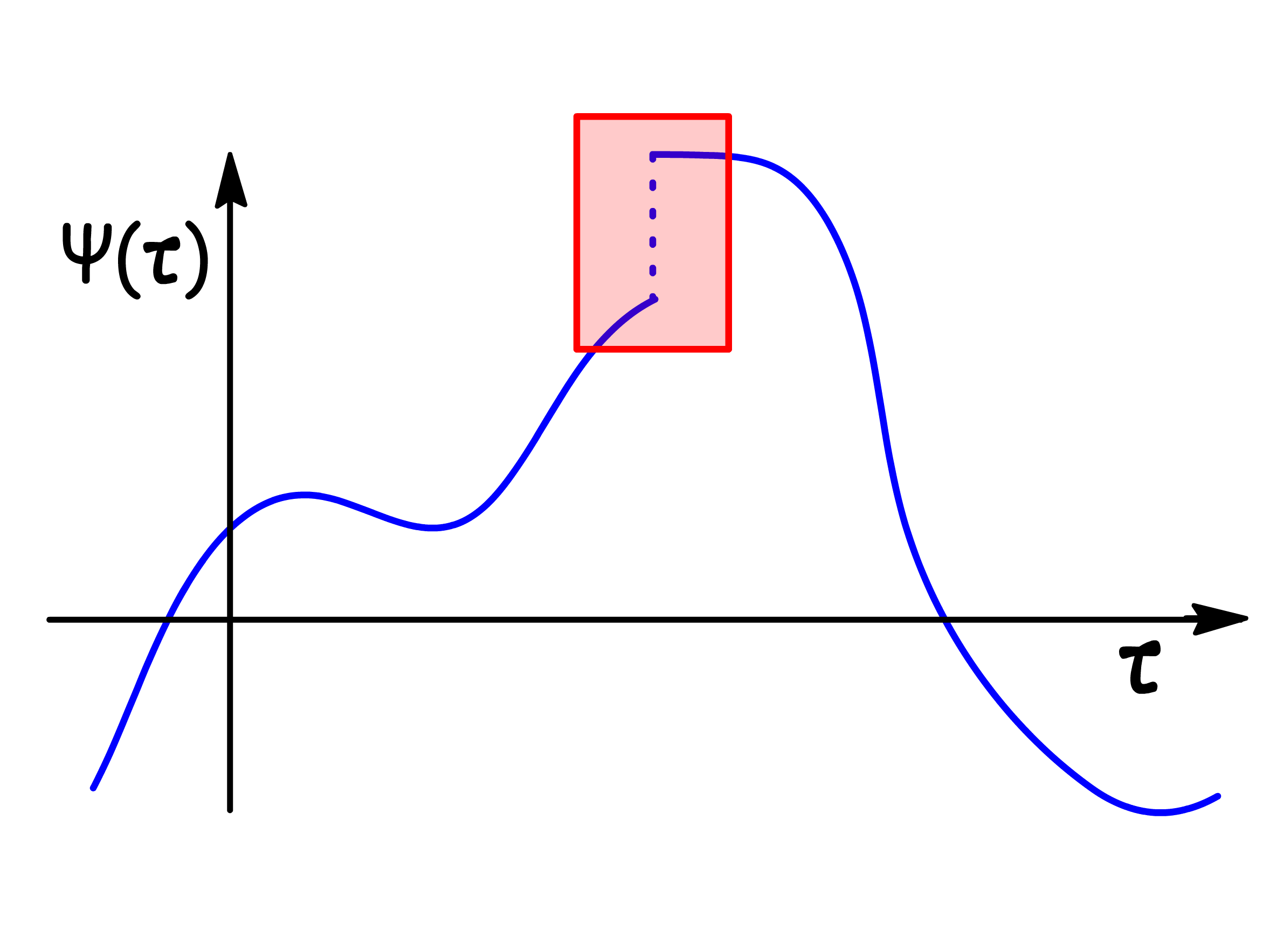
The Born interpretation puts several constraints on the acceptibility of wavefunctions
-
The wavefunction must be single-valued, as there cannot be multiple probabilities for finding a particle in a region of space
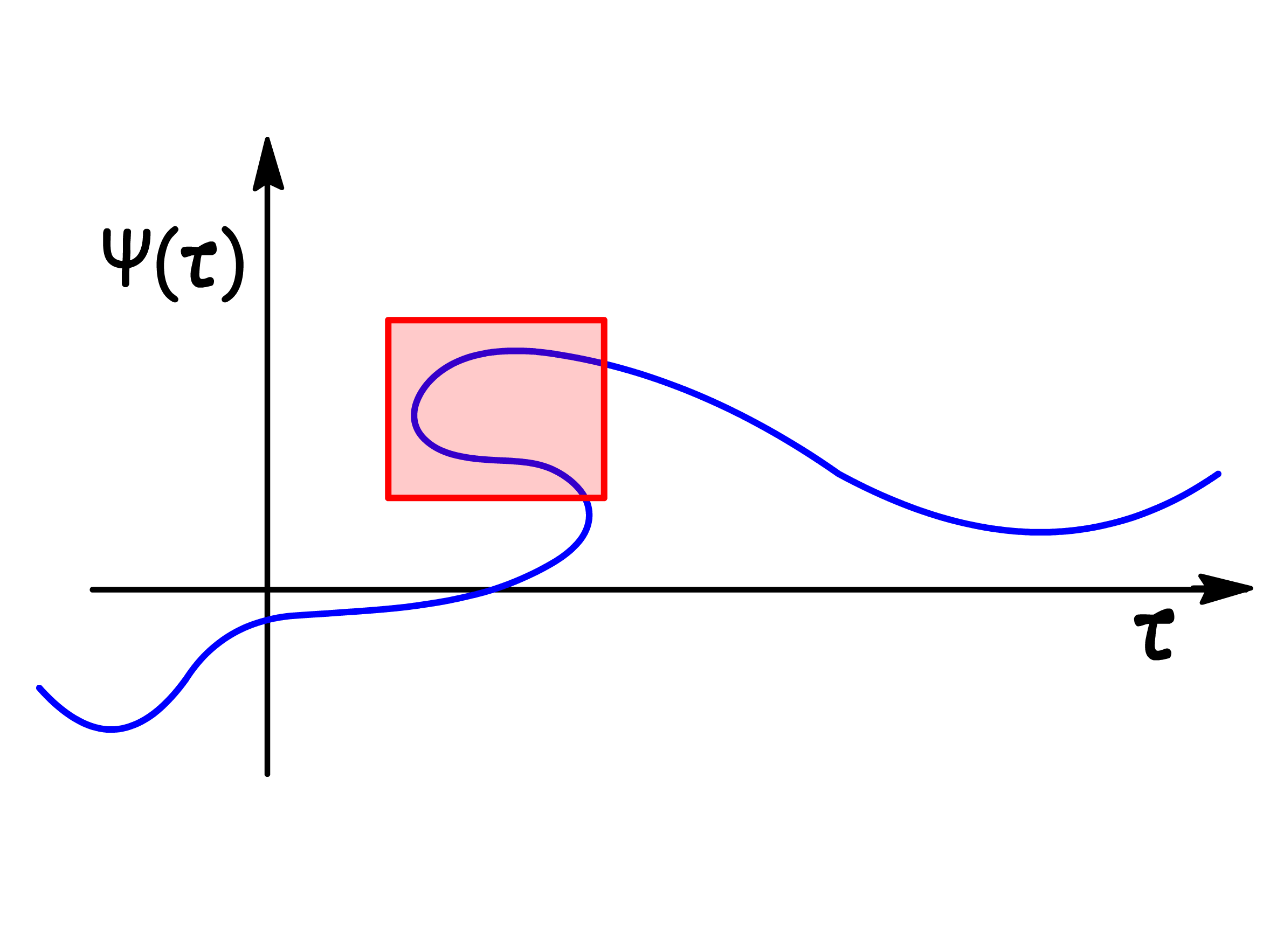
-
The wavefunction is continuous, such that is differentiable and integrable
- The wavefunction must be bounded, meaning it must not approach either positive or negative infinity. Exceptions are made for sharp spikes that rise to infinity, provided they have zero width

- Note that many wavefunctions must also be square integrable, that is, the integral of must be finite and exist. However, this is not an absolute requirement.
¶ Nodes
In quantum mechanics, a node is a point at which the wavefunction is exactly zero
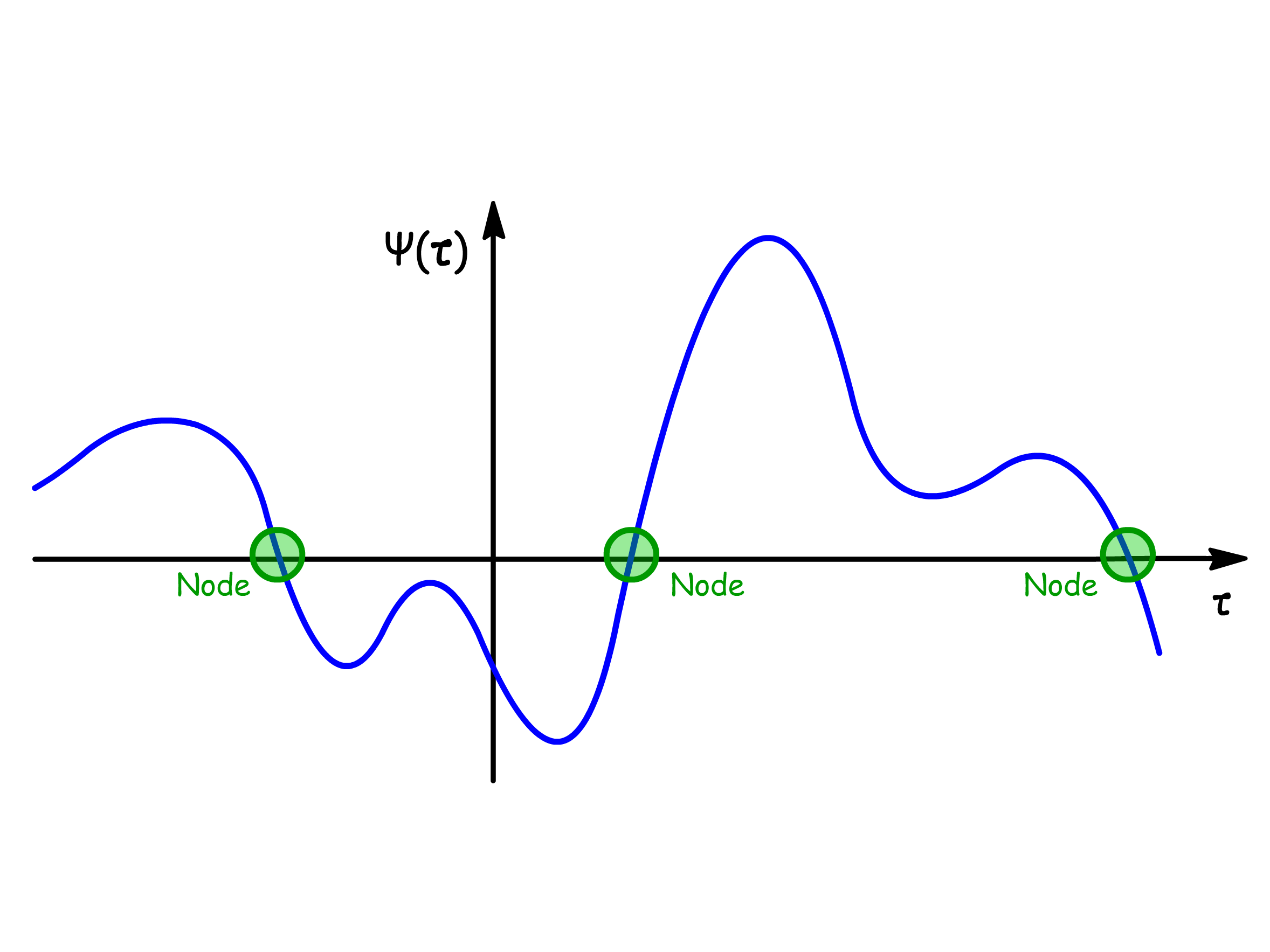
- The boundaries where the wavefunction drops to zero do not count as nodes
The wavefunction always changes sign whenever passing through a node
- It is mathematically possible for functions to have the same sign of either side of the node
- However, to be a continuous function, the wavefunction must cross the axis after the node and thus changes its sign
It is impossible to find the particle at the nodes of wavefunctions
- Since the square modulus of zero is still zero, the probability density at the nodes must be zero
The kinetic energy of a particle increases with the number of nodes in its wavefunction
- This is a crucial property as we shall see that the energy of wavefunctions and orbitals increase with the number of nodes
¶ Operators in the Position Eigenbasis
We will be working mostly with wavefunctions, in other words, we will mostly be working in the position eigenbasis
- Operators are basis-dependent, so we should now determine what the operators will look like in the position eigenbasis.
- All operators can be written in terms of the position and linear momentum operator. We will start with those two
Operators are basis-dependent, so the operator takes a different form in each basis. However, its opeartion on the wavefunction in its own domain will always be the simplest
- To see the operator's form in a specified basis, we should first remind ourselves of the operator's eigenvalue equation
- The operation on the wavefunction of the operators own domain is the same as operating on the state vector in the operators eigenbasis
- Exploiting the linearity of operators, this can be rewritten as:
- Using the conjugate symmetry of the inner product, product and the fact that eigenvalues of Hermitian operators must be real, we can show that the action of an operator in its own basis is to simply multiply the wavefunction by the corresponding eigenvalue
- We can therefore conclude that the action of an operator in its own basis is to simply multiply the wavefunction by the corresponding eigenvalue
It is extremely easy to know what the position operator will look like as we are working in its own basis
- Using the above derivation, we know that the action of the position operator is to simply multiply the wavefunction by the corresponding eigenvalue
- The eigenvalue here corresponds to the coordinates of the particle in space
To determine the action of the linear momentum operator in the position eigenbasis, we need to understand the concept of linear momentum in quantum mechanics
- Wave particle duality tells us that the linear momentum of a particle is inversely proportional to the wavelength. In other words, linear momentum is directly proportional to its wavenumber
Since the wavefunction must converge to 0 at positive and negative infinity, it is not surpising that we can convert the wavefunction from the position domain to the linear momentum domain via a Fourier transform.
- In the linear momentum domain, the operator's operation is the multiplication of the value of the momentum. Our goal is to find out what the operation will become if we were to convert the wavefunction from the momentum domain to the position domain
- We shall first replace the wavefunction in the momentum basis on the left-hand side of the equation by the corresponding Fourier transform
- We can then exploit the differentiation property of the Fourier transform to obtain
- After some rearrangement, it will now become apparent that the linera momentum operator is realted to the differential/first derivative operator in the position basis
With the position basis representation of the position and linear momentum operators, we can construct the Hermitian operators of any observables in the position basis:
- This can be achieved by the substitution of the position and linear momentum in their calssical expression, by their corresponding operator in the quantum operator
¶ The Time-Independent Schrödinger Equation
The Schrödinger equation is one of the most key aspects in quantum mechanics as it allows us to relate energies and wavefunctions
- A change in energy of a microscopic system can be detected relatively easily, so it's extremely important for us to predict these energy changes mathematically
- We will only be dealing with the time-independent Schrödinger equation for now as the time-dependent case is more complex
The Schrödinger equation in essence, is an eigenvalue problem
- The observable in question is the total energy of the particle, so the eigenvalue of the corresponding Hermitian operator is the value of the energy
- The Hermitian operator here is called the Hamiltonian, and E is the total energy of the system
¶ Constructing the Hamiltonian Operator in the Cartesian Position Basis
The Hamiltonian operator must be defined in order to discuss the Schrödinger equation
- The Hamiltonian operator is just the energy operator, which can be decomposed into the kinetic energy and potential energy operators
- Since we are working with wavefunctions primarily, we will want to know the representation of each operator in the position basis
The kinetic energy operator in the position basis can be constructed from classical physics
- In classical physics, the expression of the kinetic energy of an object is given by:
- We can therefore find the kinetic energy operator by replacing linear momentum in the classical expression with the linear momentum operator in the position basis
- We live in a three-dimensional space, so we can expand the second partial derivative of the position basis in 3D cartesian coordinates.
- For simplicity's sake, we often write the sum of the second partial derivatives as the Laplacian operator.
Note the laplacian is the dot product of the del operator/nabla with itself
- Since the kinetic energy operator of the Hamiltonian funciton is a second-order derivative, the kinetic energy of a particle is related to the curvature of the wavefunction. Moreover, the region of the wavefunction that is sharply curved will have a greater contribution to the total kinetic energy. The number of nodes present in a wavefunction is usually a good indication of its curvature, so loosely speaking, the more nodes a wavefunction has, the higher its energy
The potential energy operator in the position basis can be constructed from classical physics
- We know that potential energy varies with position, meaning it is a function of position. Hence, the action of the potential energy operator in the position basis is to simply multiply the wavefunction by its classical function
- The potential energy of each system varis greatly, so there is no generalised expression for the classical potential energy function.
Having acquired both the kinetic and potential energy operators, we are now able to write the time-independent Schrödinger equation
- The Hamiltonian in the position basis is given by
- With the Laplacian in Cartesian coordinates
- Hence the Schrödinger equation in the position basis is given by
- The Schrödinger equation is therefore nothing but a second order differential equation
¶ Constructing the Hamiltonian Operator in the Spherical Position Basis
So far, the implicit choice of basis is the Cartesian coordinates
- This worked because the motion along each axis is independent from each other in most cases, so we can solve the Schrödinger equation through the method of separation of variables
- However, in the case where the Cartesian coordinates are changing simultaneously, we are unable to separate the motion along each individual axis
- Hence, it is sometimes more convenient to use the spherical coordinate system, where the variables are , the radial distance, polar angle and azimuthal angle.
Our goal is to convert the three-dimensional kinetic energy operator from Cartesian to spherical coordinates.
- In Cartesian coordinates
- We know that the Cartesian coordinate system can easily be transformed to spherical coordinates using the following relations
- Using the chain rule, we can write down each partial derivative in terms of the independent variables of spherical coordinates
- We are interested in the sum of the second partial derivatives, which is written as:
- Hence, the kinetic energy operator in spherical coordinates can be written as:
- To save time writing, we define a new quantity to represent the terms of angular dependency:
- is known as the Legendrian operator and determines the contribution to the kinetic energy of motion at constant distance from the coordinate cente
- We can therefore create the equality
- is known as the Laplacian operator (Sometimes denoted ), and is used in many other famous physical equations, such as Poissson's equation. The Laplacian has different forms in different 3D coordinate systems (most notably, cartesian, spherical polar and cylindrical polar).
NOTE: can be rewirtten using implicit differentiation as:
The potential energy operator in the position basis can be constructed from classical physics
- However we now need to express the function of potential energy in spherical coordinates
- the potential energy of every system varies greatly, and there is no generalized expression for the classical potential energy function
Hacing acquired both the kinetic and potential energy operators, we are now well-positioned to construct the time-independent Schrödinger equation in spherical coordinates
- The Hamiltonian in the position basis is given by
- Hence, the Schrödinger equation in the spherical polar position basis is given by
- The Schrödinger equation is therefore nothing but a second-order partial differential equation
¶ The Hamiltonian Operator in The Cylindrical Position Basis
Similarly, the Hamiltonian can be written in cylindrical polar coordinates.
- Motion in a cylindrical system is a function of the variables : The radial distance, polar angle and vertical displacement respectively
- The Cartesian variables can be transformed to their cylindrical polar counterparts as follows: (this is consistent with 2D polar coordinates)
- As seen in the above examples, we can use the Laplacian to construct the kinetic energy operator. In the cylindrical basis, the Laplacian is given by
Note can be rewritten using implicit differentiation as
- Hence the kinetic energy opereator in the cylindircal basis can be written as
- Specifying the potential energy function to cylindrical coordinates, the Hamiltonian can be written as
- Hence, the Schrödinger equation in cylindrical polar coordinates is given by
- As we will see when modelling motion of a particle on a ring, the radial and vertical displacement dependence disappears, giving a second order differential equation with angular eigenfunction solutions.
¶ Solutions to the Schrödinger Equation
Although we have already placed some restraints on the acceptability of the wavefunction using the Born-interpretation, there has been no requirement that an acceptable wavefunction must satisfy any particular eigenvalue equation
- If the wavefunction is a stationary state, meaning that its probability distribution does not change with time, then it should always satisfy the Schrödinger equation
- Hence, we can see whether a wavefunction can represent a system by simply examining whether said wavefunction is one of the eigenfunctions of the Hamiltonian operator
The Hamiltonian operator is a combination of the kinetic energy operator and the potential energy operator. The kinetic energy operator is always the same, but the potential energy operator depends on the system
- The exact form of the potential energy operator determines if the Schrödinger equation is exactly solvable. If it is, there is an analytic solution. However, in many cases, it is not solvable analytically and must be approximated
A system usually has not just a single wavefunction, but a whole set of possible wavefunctions
- Each wavefunction has an associated energy and other eigenvalue observables
Since the Schroedinger equation is a linear differential equation, any linear combination of wavefunctions will also be a solution, by the property of superposition
- We have already encountered this when dealing with classical waves. What is new is the interpretation of the superimposed state
- In the case of classical waves, the superimposed wave will have very different attributes from the original waves. However, in quantum mechanics, a superimposed state will have measurements that lead to results of the original states
When solving the Schrödinger equation, there may be different wavefunctions that share the same eigenvalue energy
- Linearly independent wavefunctions that have the same energy are called degenerate
- In general, if N wavefunctions correspond to the same energy, we say the state is 'N-fold degenerate'
There are two types of degeneracy: degeneracy by symmetry and accidental degeneracy
- Degeneracy is almost always associated with symmetry in real systems
- Degeneracy by symmetry occurs because symmetry allows independent elements to be equivalent such that their eigenvalues will be the same
- Accidental degeneracy is a kind of degeneracy that occurs as a result of certain unique characteristics of the system or the functional form of the potential under discussion. It is related possibly to a hidden dynamical symmetry in the system
We know that eigenvectors of Hermitian operators are orthogonal if they have different eigenvalues
- Hence, non-degenerate wavefunctions must be orthogonal
- Any linear combination of degenerate wavefunctions is also an eigenstate corresponding to the same eigenenergy. Hence, we can make degenerate wavefunctions orthogonal via the Gram-Schmidt Orthogonalization method