In this chapter, we will showcase a few hypothetical situations that demonstrate quantum mechanical phenomenon
- These models can be used to approximate real microscopic situations
- We will introduce many new and important quantum mechanical concepts that are applicable to almost all of quantum chemistry
- We will later present the crucial features of the solution of the Schrödinger equation for translation, one of the basic types of particle (and atomic/molecular) motion
- We will see that quantization emerges as a natural consequence of the Schrödinger equation and the conditions imposed on it
¶ Free Motion in One dimension
We shall begin our journey by considering the simplest motion possible, a single particle travelling in one dimension with no constraints
- By convention, we will chose the path the particle is travelling along as the x-axis
¶ Wavefunction
We shall construct the Schrödinger equation for this motion in the Cartesian coordinates
- Since we are working along the x-axis, the kinetic energy operator should only be differentiating with respect to x
- The particle is moving freely without constraints, so the potential energy experienced by the particle should not vary with space, which means the action of the potential energy operator amounts to multiplying by zero
- Hence the Schrödinger equation should have the following form
Before we start solving for the wavefunctions, we should first simplify the Schrödinger equation
- The Schrödinger equation is just a linear differential equation, so we should first write it in its normal form
- We know that the particle does not possess any potential energy, so the total energy is equal to the kinetic energy of the particle, which can be expressed in terms of the linear momentum
- Using the wave-particle duality property, we know that linear momentum in quantum mechanics is given by the product of the wavenumber and the reduced-Planck's constant
- Cancelling out the terms will give us a simplified Schrödinger equation
After the simplification, it should be apparent that the Schrödinger equation here is nothing but a second-order linear homogeneous equation with constant coefficients
- We know the unknown function must have the form
- The characteristic equation of the differential equation is
- Solving the characteristic equation gives us a pair of complex conjugate roots
- Hence the general solution is given by the linear combination
- Where A and B are normalization constants of the wavefunction respectively
The values of the constant A and B in a particular solution depend on how the state of motion of the particle is prepared
- If the particle is travelling towards the positive x-axis, then its linear momentum is , and the wavefunction is directly proportional to . In this case and is a normalization factor
.- If the particle is travelling in the direction of the positive x-axis, then its linear momentum is , and the wavefunction is directly proportional to . In this case and is a normalization factor
- If the particle is travelling in the direction of the negative x-axis, its linear momentum is , and the wavefunction is directly proportional to . In this case, and is a normalization factor
¶ Energy of the particle
Since the particle is travelling without constraints, using it as a reference, every point in space is identical
- It possesses no potential energy, and its translational kinetic energy is equal to the total energy
The wavefunction is an eigenfunction of the Hamiltonian operator, so the energy of the particle can be found by solving for the corresponding eigenvalue
- If we plug our wavefunction general solution into the Schrödinger equation, we have
- Evaluating this expression by differentiating, we obtain
- Canceling out the wavefunction leaves us with our expression of the energy
- This is the same conclusion we arrived at when substituting classical linear momentum for it's quantum mechanical expression,
We can see that the kinetic energy of a particle is proportional to the square of its wave number
- We know that the wave number is inversely proportional to the wavelength of the wavefunction, so we know that the kinetic energy is also inversely proportional to the wavelength
- We can therefore conclude that region of the wavefunction with a greater curvature corresponds to a larger magnitude of kinetic energy
In the above expression, the kinetic energy only changes with the value of the wave number
- Like the wave number, kinetic energy can take on any real positive values
- Hence, the energy of the particle is continuous, or not quantized
- Quantization does not apply in this situation because there are no constraints on the particle
¶ Probability Density of the Particle
The probability density function of the position particle is given by the square modulus the wavefunction
- We can then substitute in the wavefunction solution we just derived
- By expanding this expression, we get
- When A is non-zero, B must be zero, and when B is non-zero, A must be zero. Hence there are two solutions
- In this situation, the probability density of the particle is a constant
We can see that the probability density of the particle is uniform if the particle is in pure momentum states of or
The function of probability density is a straight line that is parallel to the x-axis, meaning the probability of finding the free particle is identical in every bit of space
When normalized, the area under the probability density function should amount to 1, meaning the square of A times the length of the whole x-axis (infinite) should equal 1, which is not possible
This result is consistent with the Heisenberg Uncertainty Principle
- Knowing precisely the momentum of hte particle along the x-axis, makes us oblivious to the position of the particle on the x-axis
¶ Confined Motion in a One-Dimensional Box
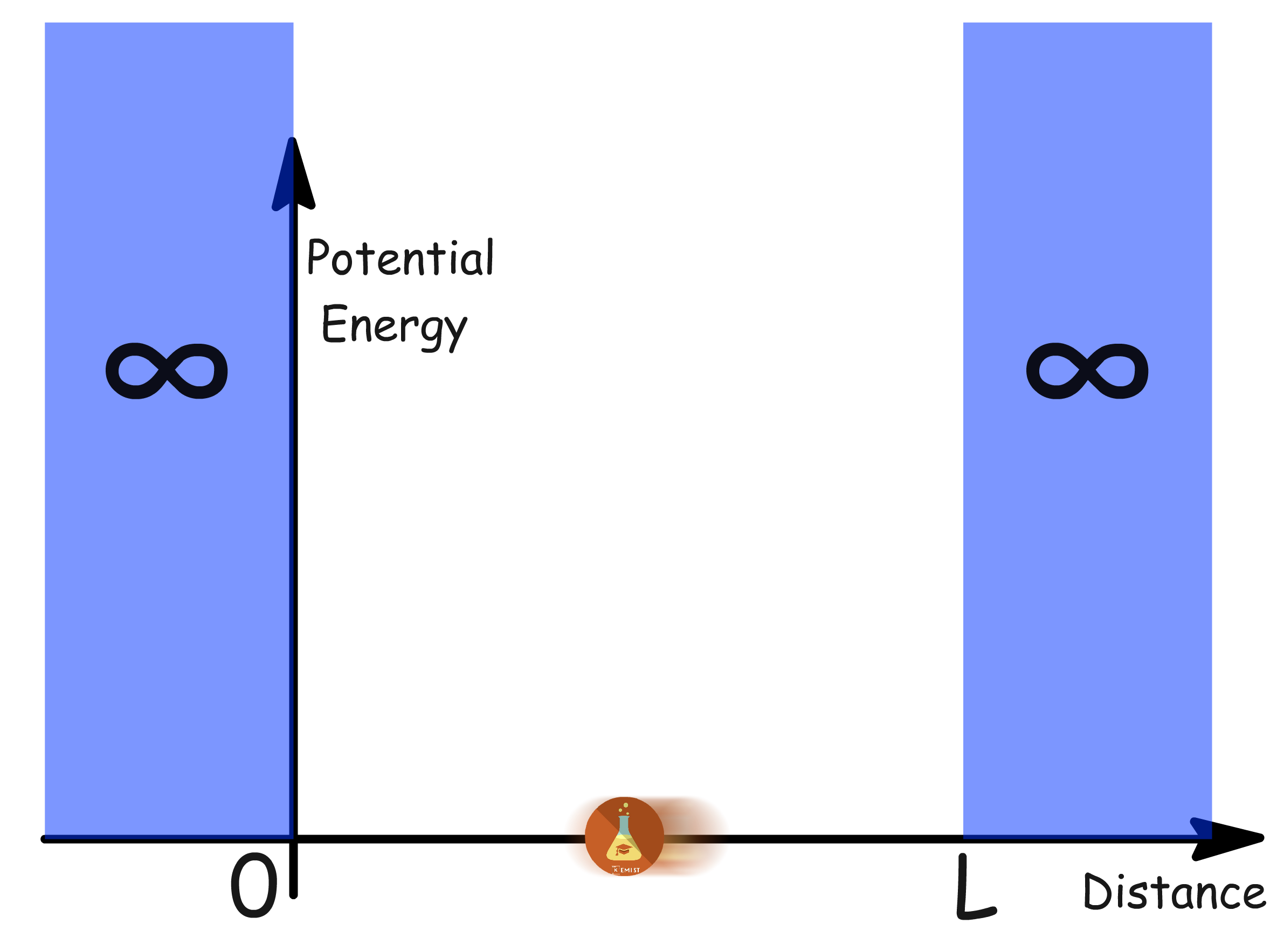
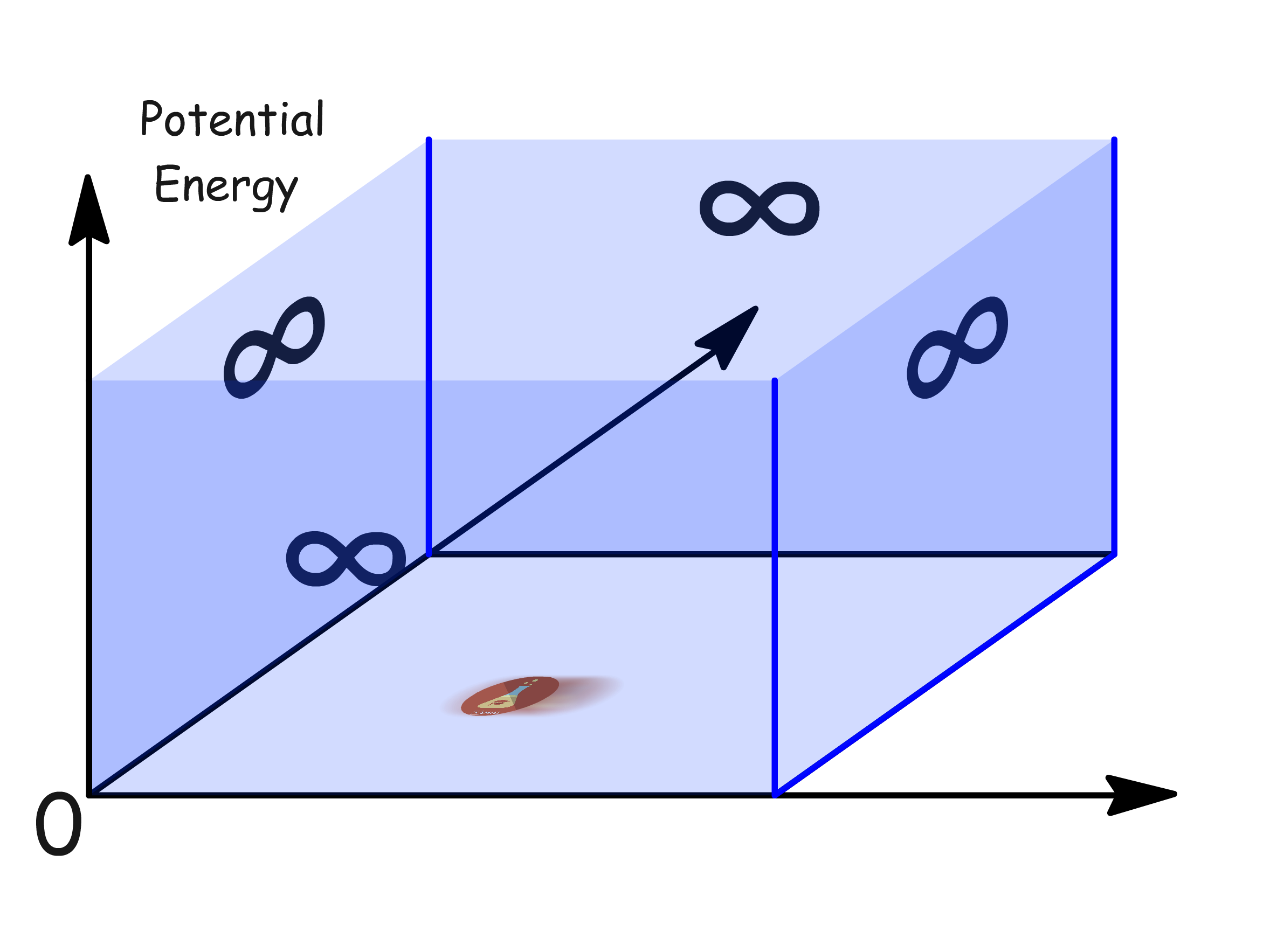
Consider a single particle confined within a finite region of one-dimensional space between two impenetrable walls (of infinite potential energy)
- The walls are situated at and an arbitrary point,
- The potential energy at and rises abruptly to infinity - serving in effect as a wall
- The particle cannot go through the 'walls', making it seems as though the particle is confined within a one-dimensional box
- Note that although the diagram is two-dimensional, the particle can only move along the x-axis, because the y-axis is potential energy of the particle at different point in space
¶ Wavefunction
We can construct the Schrödinger equation for this motion
- Since we are working along the -axis, the kinetic energy operator should only be differentiated with respect to just like before
- The box ensures that the particle experiences zero potential energy within the box, but infinite potential energy outside of it
- Hence , we will have two Schrödinger equations; one for inside and one for outside the box
It should be noted that E must take on the same values for both of these equations
- The eigenvalue E pertains to the entire range of the particle and is not influenced by divisions we make for mathematical convenience
In order to satisfy the Schrödinger equation outside the box, we need to eliminate the infinity
- Although the eigenvalue energy of the particle outside the box is non-zero, the probability density of the particle in those regions is zero
The Schrödinger equation inside the box is the same as that of a free particle, so the general solution is also the same
- It is more convenient to express it in terms of its sinusoidal form
- We can simplify the expression
- Writing as C and as D, we get
Although the wavefunction appears to be acceptable in the eyes of the Schrödinger equation, we have yet considered the restrictions on the system
- We need to employ some boundary conditions to the system
The requirement of the continuity of the wavefunction implies that the wavefunction must be zero at the walls
- Hence, the two boundary conditions or constraints on the function are
- The wavefunction must be continuous, so the wavefunction should curve to zero at and
Setting to 0, we get
- This tells us that , so and the wavefunction can be written as
- Setting to 0, we get
- We can simply set D to zero to satisfy the equality, but doing so will cause the entire wavefunction to be zero in every bit of space. This would in turn means that the probability density of the particle is zero in every bit of space, which is impossible
- The alternative is to make the sine term zero. In terms of radian, this will only occur when the product of k and L equals nπ, where n can be any positive integer. Hence, we can redefine the wavenumber in this situation as
- We can then substitute for the wavenumber in the wavefunction
The wavefunction is still incomplete as it needs to be normalized
- Although the inner product is defined as an integral across all space, the wavefunction is zero outside the box, so it is the same as an integral between x = 0 and x = L
- The norm is given by
- Hence the normalized wavefunction is
A quantum number is an integer that labels the state of the system
- Since can only take on integer values, it is by definition, quantized. We can therefore call a quantum number
- In this situation, there is an infinite number of acceptable solutions, and the quantum number specifies any one of interest
We are restricting n to be any real positive integer,
- cannot be zero, because in doing so, the wavefunction will equal to zero at every point in space, which violates the Born interpretation
- cannot be a negative number as it is the product of the length of the box and the wavenumber, both of which must be positive
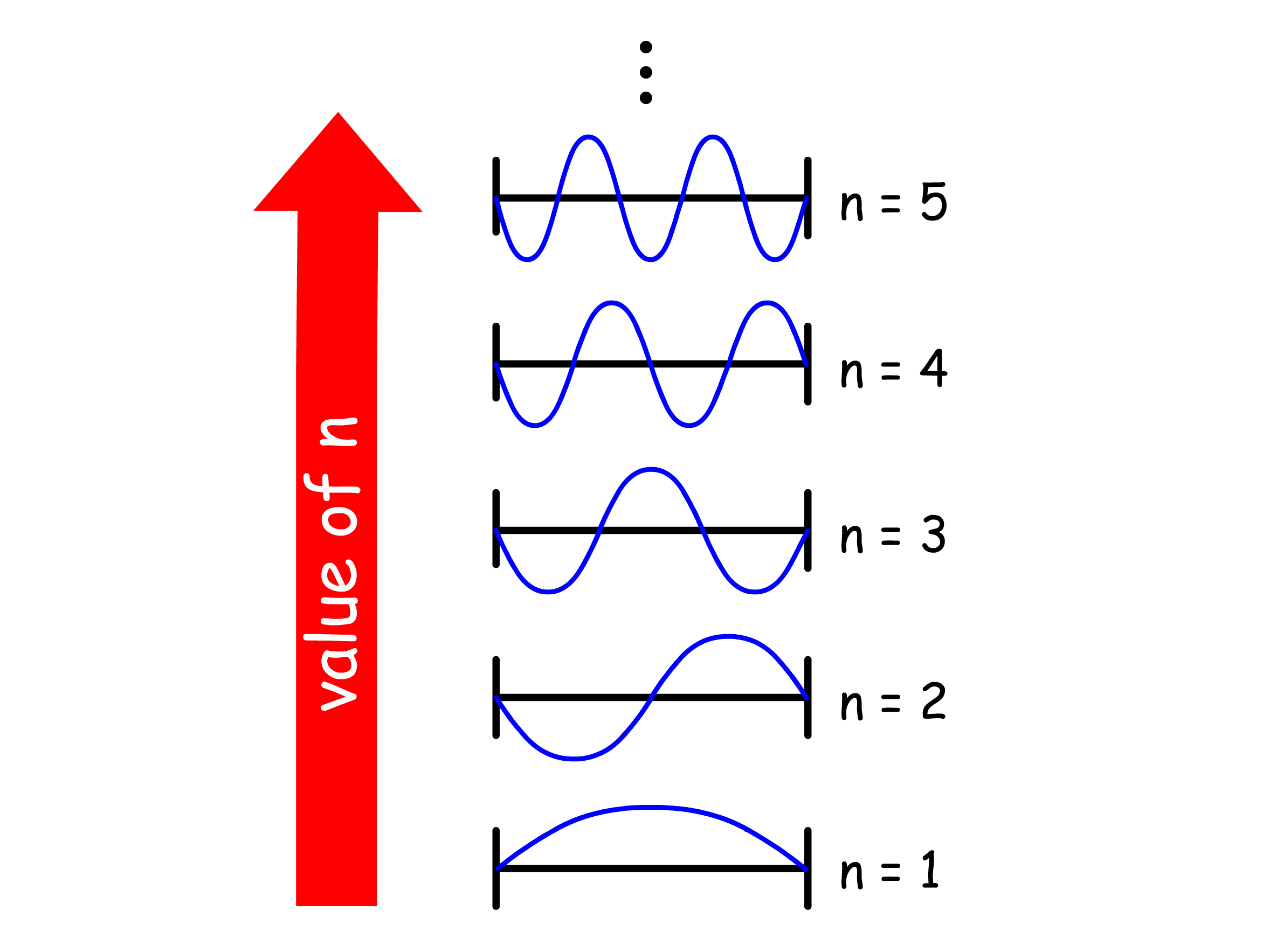
The wavefunction shows that the particle will have a standing wave-like behavior when confined within the box
- As we increases the value of , the number of nodes in the wavefunction increases
- Regions of the wavefunction where the curvature is high are associated with a higher kinetic energy and we can see that the average curvature of the wavefunction increases with
- We can therefore conclude that the kinetic energy of the particle increases as the number of nodes increases
¶ Energy of the Particle
With the newly defined wave number, we can also define the linear momentum of the particle in terms of the quantum number
- The linear momentum in this situation is still the same as that of the particle travelling freely without constraint
- We can then substitute the wavenumber in terms of the quantum number
Since the particle is travelling without constraint within the box, every bit of space is idential within the box from its point of view and therefore it possesses no potential energy
- Although its potential energy will be infinite outside the box, the probability of finding it there is also zero
- Therefore, its total energy is equal to its translational kinetic energy
Since the Schrödinger equation inside the box is the same as that of the situation where the particle is moving without constraints, the should have the same expression for energy
- We have shown that the wave number is expressed differently in this situation
The kinetic energy and linear momentum of the particle is quantized since n can only take on certain values
- Confinement acts as filter, restricting acceptable solutions and leading to quantization
- Since the lowest possible value of the quantum number, , is 1, the lowest possible energy of the particle is non-zero. This lowest, irremovable energy is called the zero-point energy
The physical origin of the zero-point energy can be explained in two ways:
1.The Heisenberg Uncertainty Principle forbids particles that are confined within a finite region to be stationary
- Since the position of confined particle is not completely undefined, the uncertainty in their momentum must not be zero,
- This shows that when there is uncertainty in momentum, the value of linear momentum must be non-zero, implying a non-zero kinetic energy
- If the wavefunction is to be zero at the walls, but smooth, continuous and non-zero within the box, then it must have curvature
- Curvature of the wavefunction implies it must have a non-zero kinetic energy, since curvature and the expression for a particles kinetic energy are both dependent on the wavenumber,
¶ Probability Density of the Particle
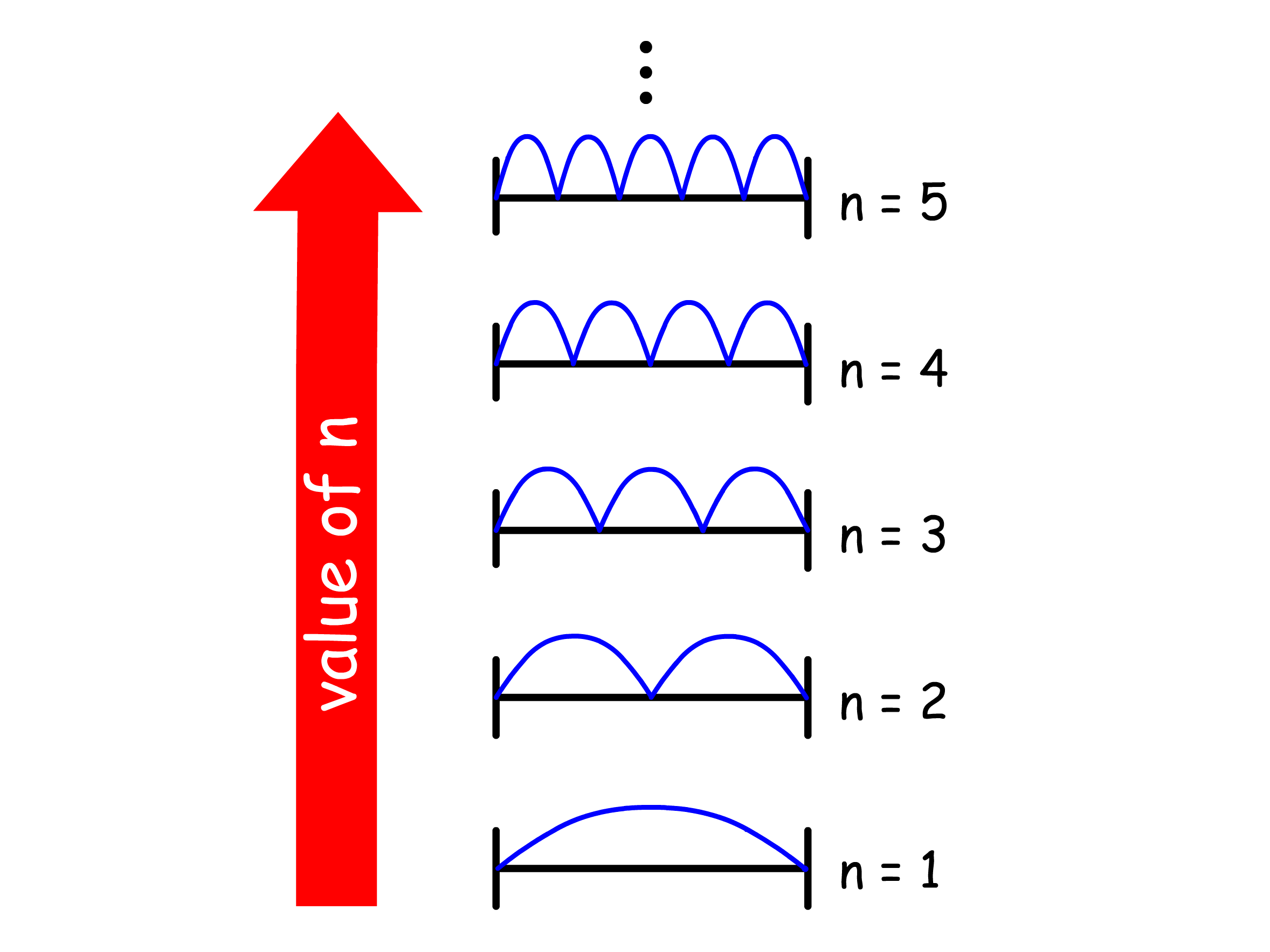
The probability density of the particle in the box changes with the quantum number
If we are viewing the particle in a box as a classical physics problem, we should expect the particle to bounce off the wall and reverse its direction
- However, the fact that there are nodes within the box means that the particle has to somehow travel across the box while not travelling through certain regions as if it is teleporting
The non-uniformity in the probability density is pronounced when n is small
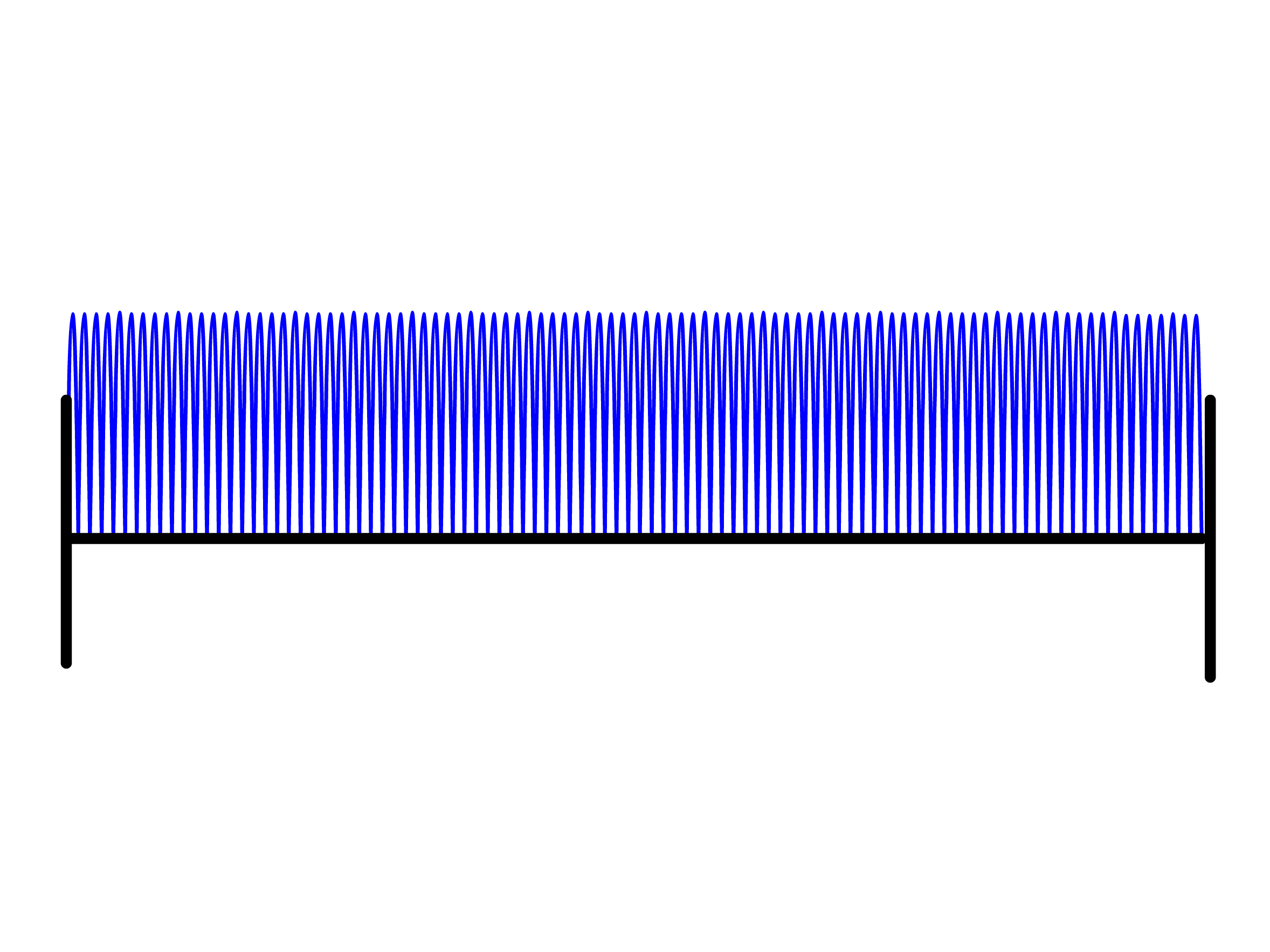
- The probability density at high quantum number reflects the classical result that a particle bouncing between the walls spends, on average, the same amount of time at every point in space
Quantum results corresponding to the classical prediction at high quantum number is an illustration of the correspondence principle
The correspondence principle, states that classical mechanics emerges from quantum mechanics as the system reaches higher energy levels, with higer principal quantum number,
- The correspondence principle demonstrates itself when we examine the separation between adjacent energy levels of and :
- The separation in energy decreases as the length of the container increases, and approaches zero when the container has macroscopic dimensions (large )
- This explains why atoms and molecules are free to move in the macroscopic level and can be treated as though their translational energy is not quantized
¶ Confined Translational Motion in Three Dimensions
Now that we have familiarized ourselves with situations happening in the one-dimensional world, we can move on to solving quantum mechanical problems in higher dimensions
- We will take a look at quantum situations in three-dimensions as we live in a three-dimensional world
- Particularly, we will examine the confined motion of a particle in a three-dimensional box
The confined motion of a particle in a box has the same basic principles for two or more dimensions, the only difference being the addition of more axes of motion
We should now consider a rectangular two-dimensional region of a surface with length in the -direction, in the -direction and in the -direction
- The potential eneergy goes to infinity when are in the ranges , and respectively
- The one-dimensional box can be easily expanded to two or more dimensions
¶ Wavefunction
The only key difference in the Schrödinger equation within the 3D box is the kinetic energy operator
- Since we are working in three dimensions, the kinetic energy operator should be with respect to all axes
- The 3D box ensures that the particle experiences zero potential energy within the box, but infinite potential energy outside it, as within the 1D box
- Hence we have two Schrödinger equations for inside and outside the box respectively
Just like in the previous 1D case, to satisfy the Schrödinger equation outside the box, the value of the wavefunction outside the box must be zero
- We will only focus on solving the Schrödinger equation inside the box
The Schrödinger equation in this situation is a linear partial differential equation, we can solve it using the method of separation of variables
- If we now put the wavefunction into each partial differential equation, the function(s) that does not vary with the variable will be constant and can be moved outside the derivative
- By dividing the whole equation by the separated wavefunction, and doing some rearrangement, we can make sure each term only depends on a single variable
- We know that each term on the left is a constant, so can equate each term with a constant by changing the energy term only
- Each of of these ordinary differential equations is the same as the 1D particle-in-a-box Schrödinger equation. Furthermore, the boundary conditions are also the same. We can therefore find the acceptable wavefunctions for each variable without any further calculation
- We know that the wavefunction is the product of the these three functions, hence
- Which can be simplified to
- The wavefunction shows that the particle will have a 3-dimensional standing wave-like behavior when confined within the box
Just like in the previous 1D case, the wavefunction contains the principal quantum number. However, here there are three due to the extension to three dimensions
- These three quantum numbers vary independently
¶ Energy of the Particle
Just like in the 1D case, the total energy of the particle is only due to its kinetic energy
- The total energy of the particle is given by the independent contribution of kinetic energy from the independent motion along the three axes
- Since the contribution of energy along each axis is the same as that of the particle in a 1D box, their kinetic energies should have the same form
For the one-dimensional box, all of the eigenvalue energies are different from one another
- However, for multidimensional boxes, since the total energy depends on not only the quantum numbers, but also the length of the box in each dimension, in some cases we yield the same energy for different combinations of quantum numbers and lengths
The degeneracy of multidimensional boxes arises from symmetry
- Whenever the lengths of the box along two axes are equal, the difference in contribution to the total kinetic energy along those two axes will only depend on the corresponding principal quantum numbers
- Whenever the set of quantum numbers adds to the same total as another set of different quantum numbers, the energy eigenvalue will be exactly the same even though different combinations of quantum numbers will give different wavefunctions
- This type of degeneracy is a consequence of a wavefunction in multidimensional space where each dimension is treated independently and equivalently
- In fact the system will achieve higher degeneracy if it has higher symmetry. In this situation, having all three sides of the box being the same length will give rise to the highest degeneracy
- Another way of thinking of degeneracy in the particle in a box case, is that we can convert between degenerate wavefunctions by simply rotating the box, which is only possible in such a system of high symmetry