¶ Trends of Main Group Organometallics
Explain the reactivity and structures of organometallics due to factors like
- Metal centre properties
- Substituent electronic and steric properties
- Physical state of the system ( solid, solution e.t.c. )
After understanding the basic principles, we can then propose synthetic routes and predict the products of given reactions
¶ Coordination Number
The coordination number of a metal center in a coordination complex refers to the number of ligands attached to the metal atom and it depends on a number of factors
1. Electronic properties substiutents
- Electron-withdrawing substituents increase the Lewis acidity of the metal center, making it more electron deficient
- Being electron-deficient enhances the tendency of the metal center to coordinate with more groups
- Consequently, electron-withdrawing groups promote a higher coordination number
2. Steric properties substiutents
- The size and shape of the ligands and substituents directly affect the accessibility of the coordination sites on the metal center. Bulky groups can hinder the approach and binding of additional ligands
- Therefore bulky substituents can kinetically stabilize complexes with low coordination numbers
3. Size of the metal centre
- Heavier metals have a larger atomic radius and greater ability to accommodate additional ligands
- As a result, heavier metals are more inclined to expand their coordination sphere
4. Inert Pair Effects
- It is observed that the metal centers of certain groups, denoted as , have a tendency to adopt an oxidation state of either or
- As we move down a group, there is a decreasing tendency to adopt an oxidation state of and an increasing tendency to adopt an oxidation state of
- This is because the two electrons in the valence s orbital will be deeper in energy as we travel down the group. Hence the energy required to promote one of the s-electron to an empty p-orbital for bonding increases down the group. Moreover, The valence orbitals become larger and more diffused down the group, resulting in ineffective overlapping. Hence, bond energies decrease down the group
- The oxidation state adopted depends on the balance between the promotion energy and the bond energy of additional bonds formed. If the promotion energy is higher than the combined bond energy of the two additional bonds, the element will be in its oxidation state. If the combined bond energy of the two additional bonds is higher than the promotion energy, the element will be in its oxidation state.
¶ Determining the coordination number
The coordination number of a metal center can often be deduced by examining the structural features of the coordination complex
- In general, unsymmetrical bridging or distorted structures tend to have lower coordination numbers compared to symmetric bridging or undistorted structures
- The presence of unsymmetrical bridging ligands or distortions in the coordination sphere indicates a reduced number of ligands directly coordinated to the metal center, suggesting a lower coordination number.
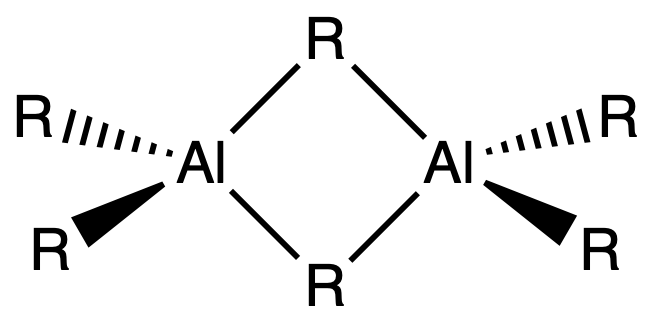
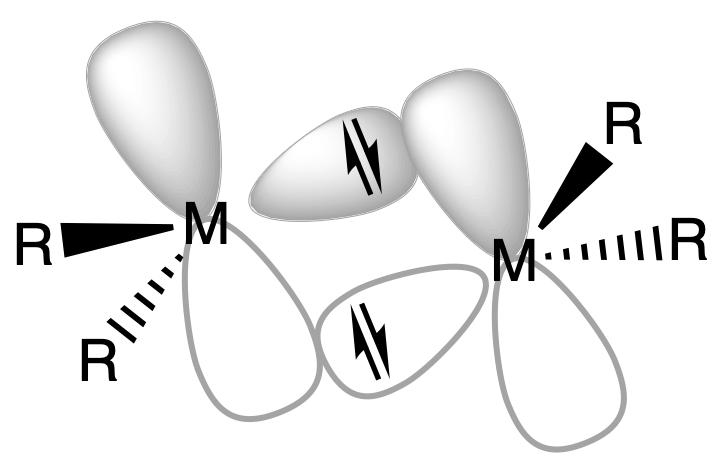
¶ Organoaluminium Compounds
Organoaluminium compounds commonly exhibit dimerization, a process in which two molecules of the compound come together to form a dimeric structure
- In general, organoaluminium compounds prefer coordination numbers greater than 3 in order to alleviate electron deficiency
- This means that aluminium tends to coordinate with more than three ligands to achieve a stable electronic configuration
- However, in the presence of very bulky R groups, three-coordinate aluminium structures can be observed. The steric hindrance caused by these bulky groups restricts the coordination of additional ligands, leading to a lower coordination number
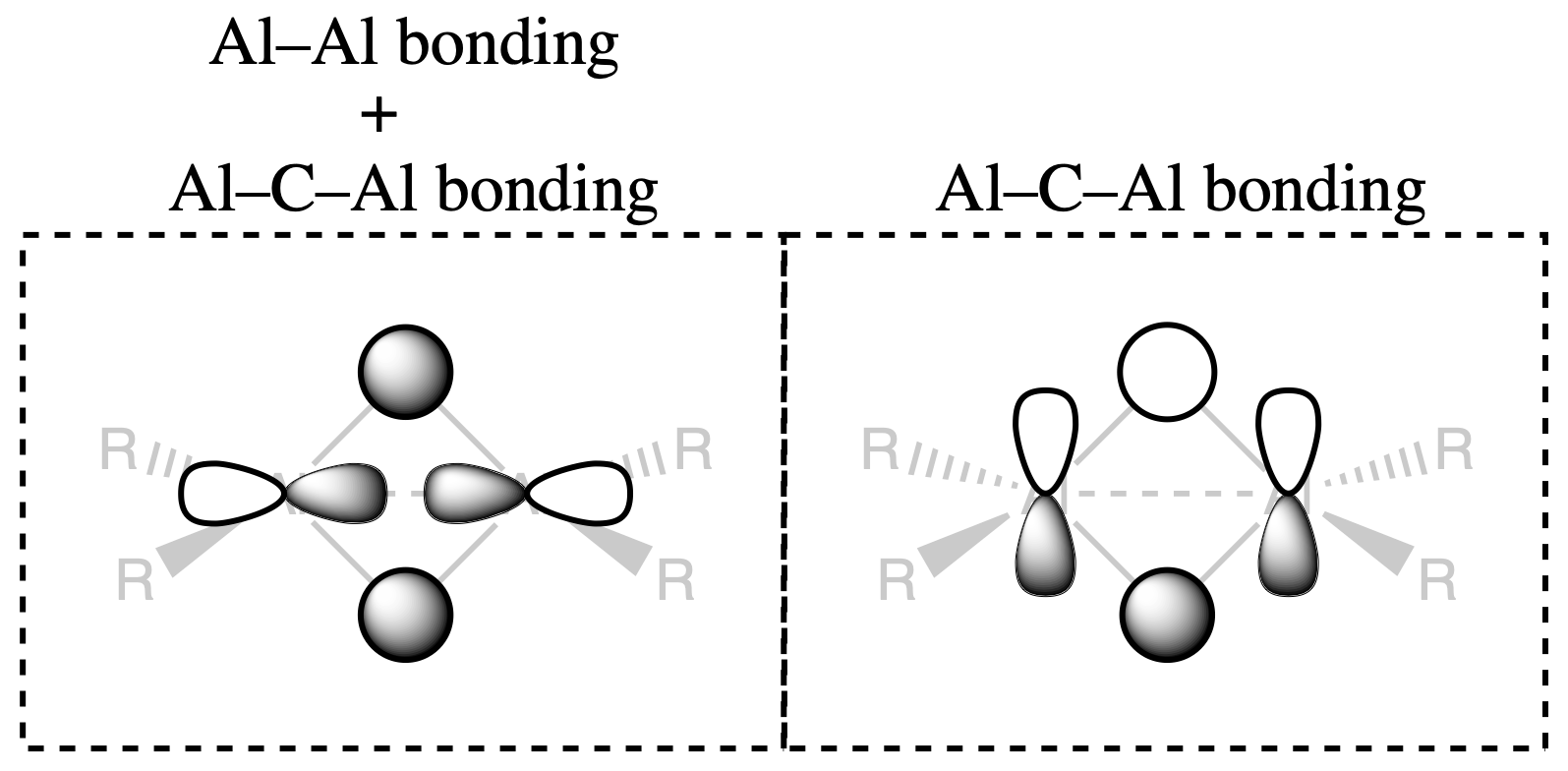
Distinct Features and MO
The dimerization of organoaluminium compounds exhibits distinct features that can be observed through various structural parameters
- The terminal bond lengths in the dimer indicate the presence of "normal" single bonds between Al and C
- These bond lengths are similar to those observed in monomeric organoaluminium compounds
- The bridging Al-C bonds in the dimer are longer compared to the terminal bonds
- The elongation of these bridging bonds signifies a reduced bond order between Al and C, indicating a weaker bonding interaction
- This weaker interaction is attributed to the delocalization of electron density over multiple aluminium atoms in the dimeric structure
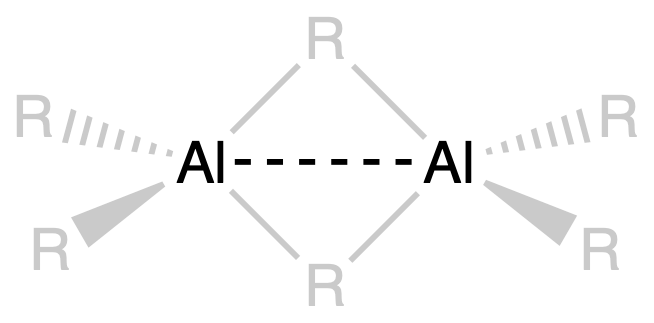
- The Al-Al distance in the dimer suggests the presence of some bonding between the two aluminium centers
- The proximity of the metal centers in the dimer indicates a weak interaction or bonding between them, contributing to the overall stability and structural integrity of the dimeric structure
These features are in agreement with the molecular orbitals
Dynamic Association
The dimeric structure of organoaluminium compounds allows for the exchange of bridging R groups with terminal R groups
The rate of exchange increases with temperature, as indicated by NMR spectroscopy.
- At low temperatures, two distinct signals can be observed in a 1:2 ratio, as expected based on the solid-state structure. This indicates that the exchange of the terminal and bridging groups is relatively slow compared to the timescale of the NMR measurement. The two signals arise from the different chemical environments experienced by the terminal and bridging R groups in the dimer.
- As the temperature is increased, the exchange process becomes faster, and at high temperatures, the NMR spectrum shows a single "average" signal. This indicates that the exchange between the terminal and bridging groups is occurring at a rate that is too fast to be resolved by the NMR measurement. The rapid exchange results in the averaging of the chemical environments experienced by the R groups, leading to the observation of a single signal in the NMR spectrum
Bonding Preferences
Interactions with heteroatom lone pairs are always favored over Al-C-Al bonding
- This means that when a heteroatom, such as oxygen or nitrogen, is present and can form a coordination bond with aluminium, it will be favored over the formation of Al-C-Al bridging bonds
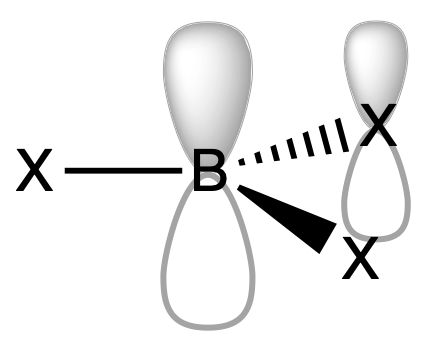
¶ Organoboron Compounds
Organoboron compounds commonly exist as monomeric species, this monomeric behavior can be attributed to several factors related to the structure and bonding of these compounds.
1. R3B
- Stabilisation by hyperconjugation of R group
2. BX3
- Stabilisation by π back-donation of X
3. R3-nBXn
- Stabilisation by a combination of hyperconjugation of R group and π back-donation of X
¶ Group 14 Dialkyls and Diaryls
Dialkyls refer to compounds where two alkyl groups are directly bonded to the central Group 14 element, while diaryls have two aryl groups bonded to the central element
- Dialkyls and diaryls of Si, Ge, Sn, and Pb exhibit similar reactivity trends to carbon analogs but with notable differences due to the presence of larger and more polarizable central atoms
The bonding model we use to describe the bonding of Group 14 Dialkyls and Diaryls is different for carbon and the rest of the group 14 elements
- For carbons, it will just be the classic double bond
- For other group 14 metal centres, we use the double donor-acceptor model
The association between the two monomers occurs through a polar dative linkage results in a trans-folded, bent structure
- The lone pair of electrons on the carbene-like monomer donates its electron density to the vacant orbital of the electron-deficient central atom of the second monomer
- This electron donation results in the formation of a coordinate covalent bond, wherein both electrons of the shared bond originate from the carbene-like monomer
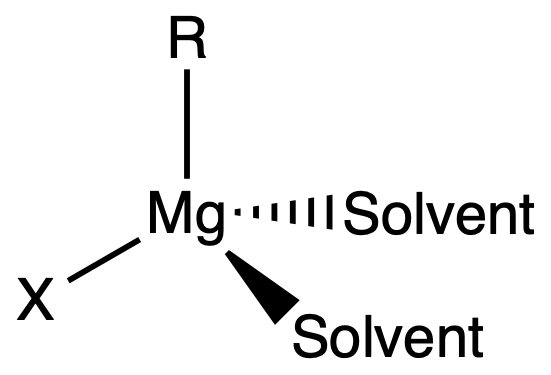
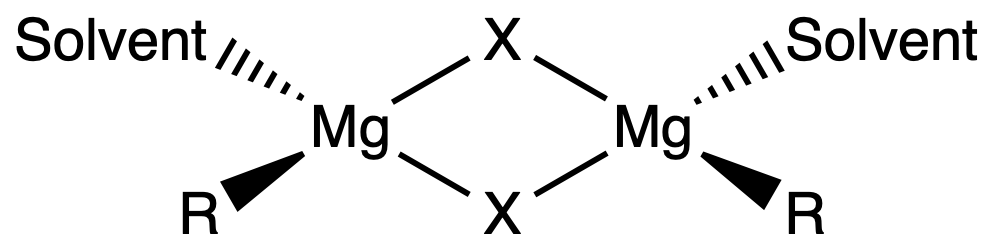
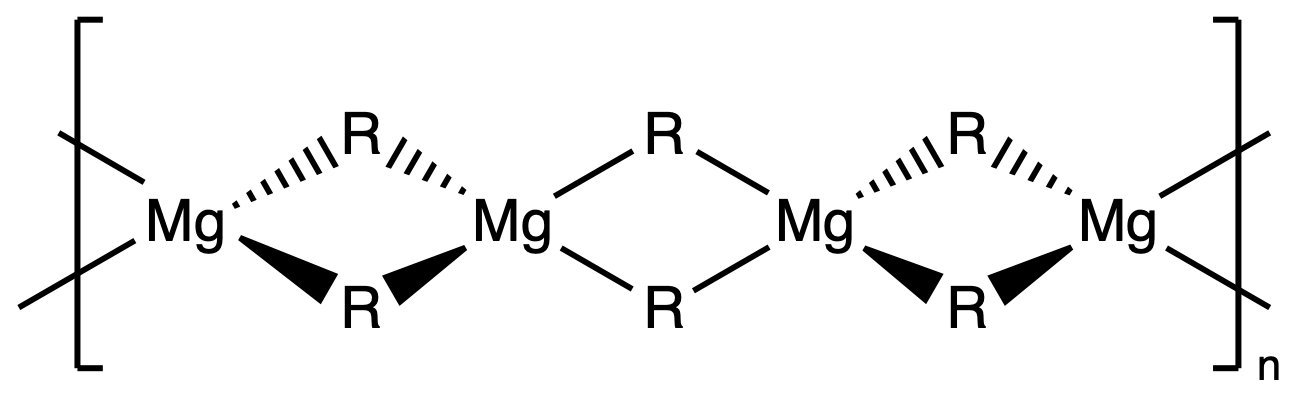
¶ Grignard Reagents
The degree of polymerization of the Grignard Reagents depend on its solvation. In general, the more solvated it is, the less polymerimerized it is
- Fully solvated Grignard Reagents have four-coordinate Mg and are solvated by two solvent molecules
- Partially solvated Grignard Reagents are oligomers featuring halide bridges
- In the solid state, unsolvated, simple R2Mg compounds generally have oligomeric / polymeric structures
Schlenk equilibrium
The Schlenk equilibrium describes the interconversion between two forms of a compound: a coordinatively unsaturated, highly reactive species and a coordinatively saturated, relatively stable species
The relative amounts of each species present in a solution depends on:
– size and electronic nature of organic group , halide
– solvent, concentration and temperature
¶ Organolithium Compounds
Organolithium aggregates in the solid state and in solution
- All organolithium compounds are electron deficient, with available orbitals for interaction with donor molecules, such as solvent molecules
- Polarity and coordinating ability of the solvent affects the degree of aggregation Li forms strong interactions with hard donors such as O (ethers) and N (amines)
Heavier Group 13 Organometallics Compounds
generally monomeric since they are less lewis acidic ( less electron deficient ) relative to Al
- Coordination can increase when there is EWG attached or when the metal centre is large
¶ Formal Cluster Compounds
¶ Polyhedral Skeletal Electron Pair Theory
Polyhedral Skeletal Electron Pair Theory (PSEPT) is a theory used to predict the structures and bonding patterns of polyhedral clusters in inorganic chemistry
- PSEPT provides a framework for understanding the arrangement of bonding and non-bonding electron pairs within these clusters
The theory takes into account several key factors
Electron Count
- PSEPT focuses on the electron count of the cluster, which is determined by counting the total valence electrons contributed by the constituent atoms
- The valence electrons are used to construct the cluster's skeletal framework.
- We shall therefore first determine the total number of valence electrons (3 per B, 1 per H), adding or subtracting electrons to take account of any overall charge
Skeletal Electron Pairs
- We assume that each boron has a terminal hydrogen
- These B-H bonds do not contibute to the overall geometry of the cluster, we therefore subtract 2 electrons for each BH unit
- After the subtraction, the remaining electrons should all be contributing to the structure of the cluster, we therefore call them skeletal electrons
- Assuming each bond has two electrons, we can divide the total number of skeletal electrons to get the number of Skeletal Electron Pairs ( SEP )
Number of Vertices in the Parent Deltahedron
For a regular deltahedron with v vertices, there are v + 1 B-B bonding molecular orbitals
- Consequently, a regular deltahedron with v vertices should have v + 1 skeletal electron pairs ( SEPs )
Wade's Rules
We can summarize the theory in a set of instructions
Determine the total number of valence electrons, considering 3 per boron and 1 per hydrogen. Adjust for any overall charge
Subtract 2 electrons for each BH unit, assuming each boron has one terminal hydrogen (2c-2e bond)
Divide the remaining number of electrons by two to obtain the number of SEPs. The number of vertices in the parent deltahedron is equal to SEP
Comparing the number of boron atoms (n) with the number of SEPs or the number of vertices determines the structural type
Placing BH Units and Hydrogen Atoms
- Each BH unit is placed on a vertex of the parent deltahedron
- If there are vacant vertices, initially those with the highest connectivity are chosen, followed by those adjacent to the vacant site
- Additional hydrogen atoms are placed bridging the B-B edges of an open face of the cluster and in extra terminal positions if a boron atom has low connectivity
- Cluster symmetry is typically maximized
- Extra Boron Atoms
- If the number of boron atoms is equal to or greater than the number of SEPs, the extra boron atoms occupy capping positions over the triangular faces
Structural Types in Clusters
In certain clusters there are fewer (or more) boron
atoms than the number of vertices in the deltahedron on which the structure is based
- Comparison of the number of boron atoms ( n ) with the number of vertices ( v ) determines the structural type
Polyhedral borane clusters: preparation, properties, reactivity
Properties:
- colourless, diamagnetic, molecular compounds
- lower members are gases at room temperature, higher molecular weight boranes are volatile liquids or solids (b.p.s similar to those of hydrocarbons of similar molecular weight)
Reactivity:
- can be extremely reactive and several are
spontaneously flammable in air- closo-boranes are much less reactive than
nido- and arachno-boranes. Some are exceptionally stable and their general chemical behaviour has suggested the term:
‘three-dimensional aromaticity’
¶ Metal Clusters
Zintl Anions
Zintl Anions are p-Block metal clusters with no substituents on the skeletal atoms
- Their structures can be explained and predicted using Wade’s rules
SEP
Each metal contains one lone pair in the outwards-pointing sp orbital, and the lone pair does not contribute to the structure
Hence, the number of skeletal electron contributed by each atom is given by
- Hence, the number of SEPs of [ Mn ]q- is given by
Transition Metal Carbonyl Clusters
Transition metal carbonyl clusters are a class of compounds that consist of transition metal atoms coordinated to multiple carbon monoxide (CO) ligands
- These clusters exhibit fascinating structures and bonding patterns that can be elucidated using the Wade-Mingos rules
Fragments
We first divide the entire complex into different fragments
- Each fragment should only contain one transition metal
- These fragments should be as symmetric as possible
Skeletal Electron Count in each Fragment
The valence electron of each fragment is found by adding the electrons contributed by the metal ( Group number of metal ) and the electrons contributed by the carbonyl ( 2 electron per carbonyl )
- Skeletal electron count of each fragment is found by subtracting 12 electrons from the number of valence electron
SEP
After finding the number of skeletal electrons in each fragment, we can sum them up, account for charge to find the total number of skeletal electrons
- Dividing that number by two gives us the number of SEP
- Using the same method as before, we can determine the structure of the cluster
¶ IR analysis of Highly Symmetrical Clusters
Group theory offers a systematic approach to determine
- The number of vibrational modes
- Whether these clusters are IR active / inactive
Vibrational Modes
To see whether certain bonds are IR-active or not, we shall start by replacing all of those bonds with a vector
We then determine the point group of the cluster and pull out the character table of said point group
We can then deduce the character of the set vectors
Using the reduction formula, we shall determine what irreps make up the set of vectors
- Check the corresponding irreps and see if there is anything in the "linear functions, rotation" column. If yes, it is IR active