¶ Crystal Lattices
A crystal can be understood as the result of combining a unit cell with a lattice structure
- The unit cell represents the fundamental building block that is repeated throughout the crystal
- The lattice refers to a regularly arranged array of points in one, two, or three dimensions that define the spatial arrangement of the crystal.
- By placing multiple copies of the unit cell at each lattice point, the crystal structure is formed.
- This process can be described mathematically as convolution, which involves overlaying the unit cell onto the lattice points to construct the crystal structure.
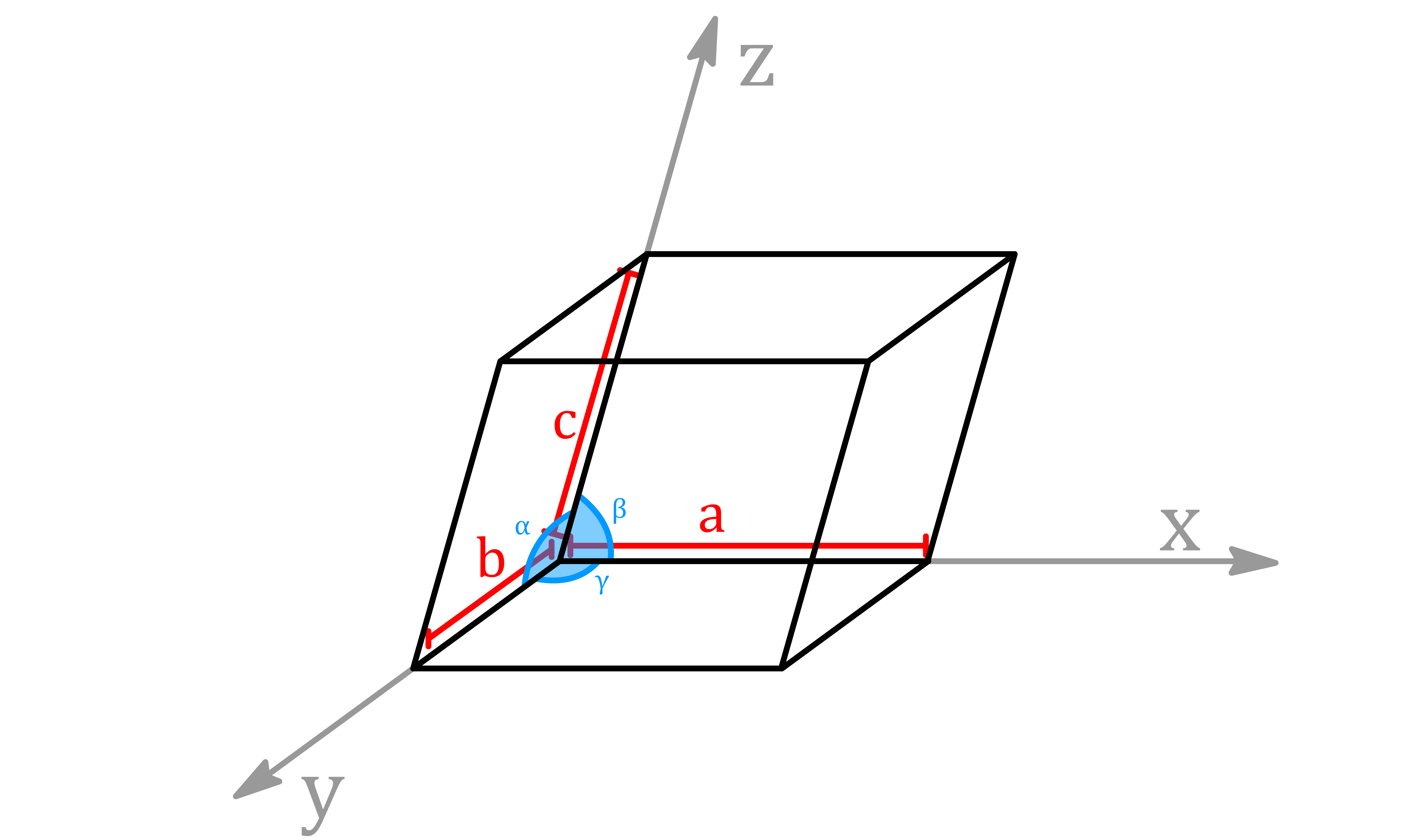
¶ Lattice Parameter
The unit cell choice defines a set of lattice parameters:
- The lengths of the sides of the unit cell ( , , )
- The angles ( , , ) between the unit cell axes
Depending on the symmetry of the cell, some of the values may be identical
A vector on a lattice, written as , is defined in terms of the unit cell parameters
- , and are positive, we denote negative values with an overbar:
¶ Lattice Symmetry Elements
Lattices in crystal structures exhibit various point symmetry elements that contribute to their overall symmetry
- These symmetry elements help describe and classify the arrangement of atoms or molecules within the crystal lattice
Mirror planes ( )
- Symmetry elements that divide the crystal into two halves, reflecting one half onto the other
- These mirror planes can exist in different orientations within the lattice and contribute to the overall symmetry of the crystal.
Rotation axes ( )
- Symmetry elements that involve rotating the crystal about an axis by a certain angle
- Common rotation axes include 2-fold ( dyad ), 3-fold ( triad ), 4-fold ( tetrad ), and 6-fold ( hexad ) axes
Inversion axes ( )
- Symmetry elements that involve inverting the crystal through a point
- Inversion axes can be described as -fold axes, where represents an integer (e.g. , )
- These inversion axes are responsible for the reflection symmetry of the crystal lattice
Centers of symmetry ( )
- Symmetry elements that involve the presence of a point in the crystal lattice that is equidistant from the surrounding lattice points
- This symmetry element represents the overall inversion symmetry of the crystal
Glide planes (a, b, c, d, n)
- Translational symmetry elements that involve a combination of a reflection and a translation
- These glide planes divide the crystal into repeated units that are translated along specific directions, contributing to the overall translational symmetry
Screw axes ( , , )
- Translational symmetry elements that involve a rotation combined with a translation along the axis
- These screw axes describe the periodic repetition and translation of the crystal lattice along specific directions
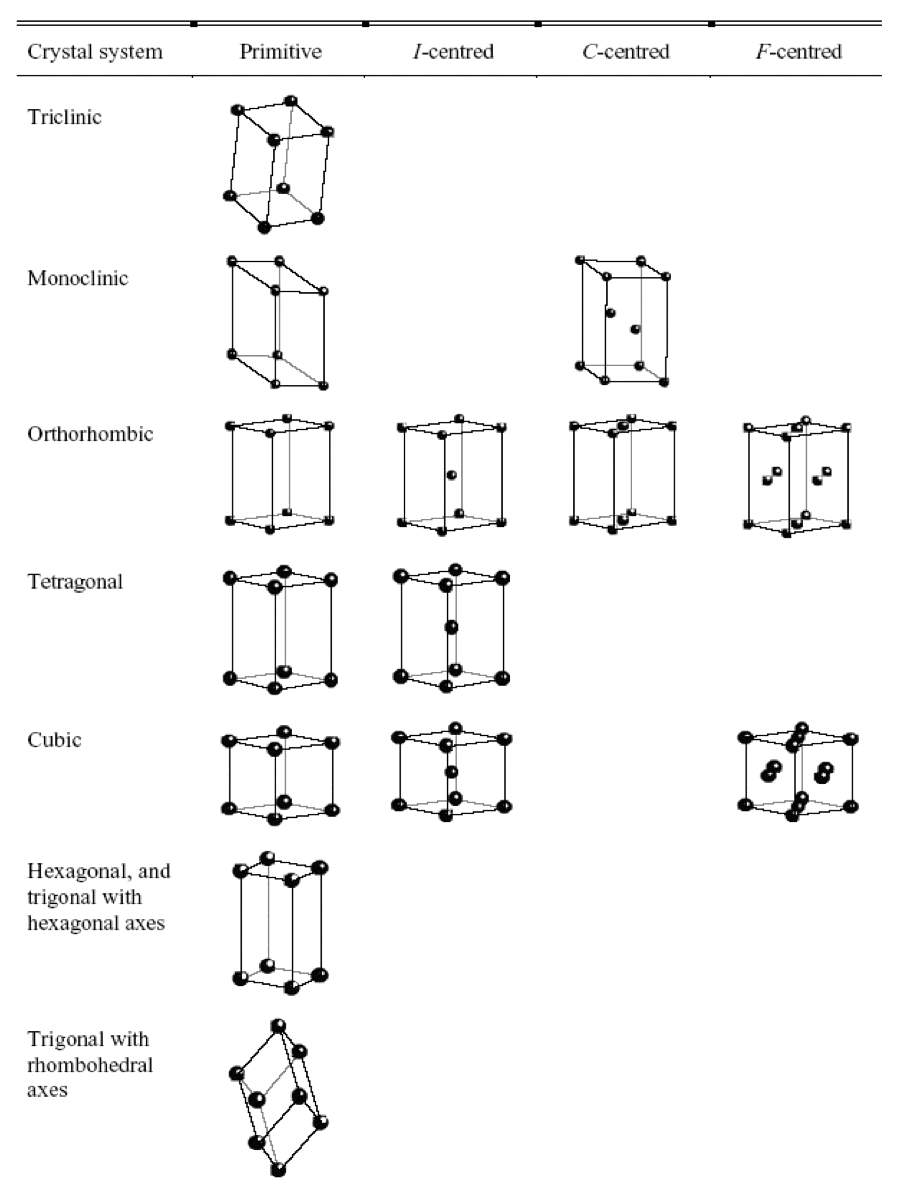
¶ Crystal Systems
In three-dimensions, there are 7 different crystal systems
Each crystal system can be further classified into primitive ( ), face-centred ( ), and body centred ( ) lattices
- The results are the 14 Bravais lattices
- All repeating 3-D structures belong to one of these classifications.
¶ Miller planes and Miller indices ( h k l )
In any lattice, it is possible to identify sets of evenly spaced planes passing through lattice points
- These planes are characterized using Miller indices , which provide a convenient notation for representing crystallographic planes
To determine the Miller indices ( h k l ) of a plane:
- Identify the plane that is closest to the origin
- Determine the intercepts of the plane with the x, y, and z axes
- Express the intercepts as fractions or multiples of a common unit length
- Take the reciprocals of these fractions or multiples to obtain the Miller indices for the plane
It is important to note that sets of equivalent planes related by symmetry are denoted by enclosing the Miller indices in curly braces, \
- These sets of equivalent planes possess the same crystallographic orientation but may be located at different positions within the lattice
We can calculate the distance ( ) between any set of planes can be calculated using the following formulas
- Triclinic :
- Monoclinic :
- Orthorhombic :
- Tetragonal :
- Cubic :
- Hexagonal :
- Rhombohedral :
¶ X-ray Diffraction from Solids
¶ Basic Principle
The wavelength of X-rays is comparable to the size of atoms and the length of chemical bonds
- This characteristic makes them well-suited for investigating the arrangement of atoms in a crystal lattice or the molecular structure of a compound.
- When X-rays interact with matter, they are scattered by the electrons present in atoms and molecules. The scattered X-rays can be detected and analyzed to obtain information about the spatial arrangement of the scattering centers
One of the key advantages of X-rays is that they exhibit wave-like properties
- When X-rays interact with a crystal, the scattered waves interfere with each other, resulting in a distinct diffraction pattern
- This diffraction pattern contains information about the arrangement of atoms within the crystal lattice, including the positions of the atoms and the distances between them
For X-rays, the scattering power of an atom, which is quantified by its atomic scattering factor ( )
- is directly proportional to the atomic number of the atom, meaning that atoms with higher atomic numbers will exhibit stronger scattering of X-rays
- It is worth noting that different isotopes of a given element scatter X-rays in the same manner ( same )
In addition to X-rays, other particles such as neutrons and electrons can also be utilized since they also possess wave-like properties
- The wavelength of neutrons and electrons can be calculated using the de Broglie equation ( )
- Neutrons, unlike X-rays and electrons, primarily scatter from atomic nuclei rather than electron clouds. This results in different isotopes of a given element exhibiting distinct scattering properties
¶ Diffraction of X-Rays from Crystals
Turns out the diffraction pattern obtained is indirectly related to the electron density distribution, within a crystal
- Specifically, the diffraction pattern is closely related to the Fourier transform of
- The Fourier Transform can be expressed as a product of the Fourier transform of within the unit cell and the Fourier transform of the lattice
- Each component represents an aspect in the diffraction pattern
- The intensities of the diffraction peaks correspond to the structure within a single unit cell, while the positions of the diffraction peaks, represented by the diffraction angles , are solely determined by the symmetry and dimensions of the crystal lattice
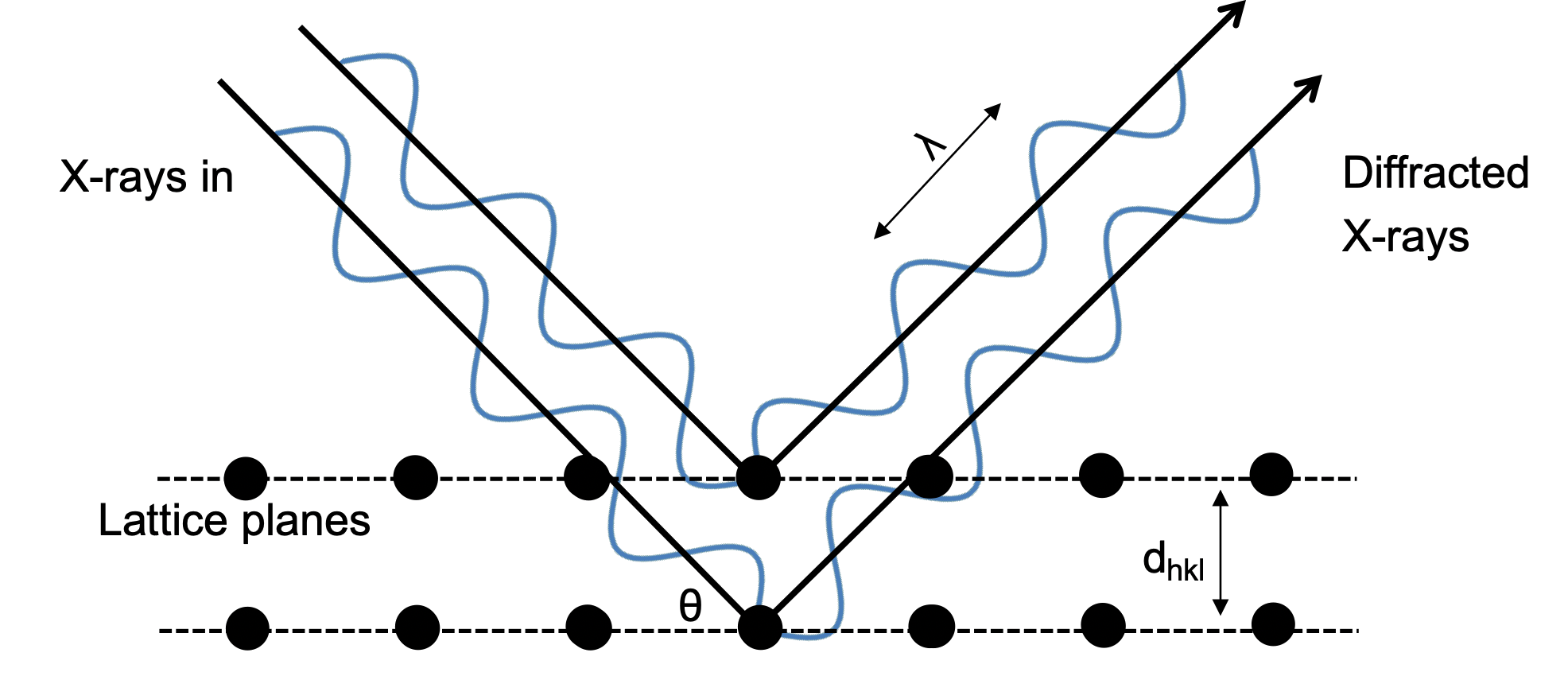
Bragg's Law
The condition for a strong diffracted beam to emerge at the same angle to a set of planes is that the scattered waves constructively interfere with each other
- Constructive interference occurs when the path difference between the waves from adjacent planes is an integer multiple of the wavelength of the X-ray beam
Systematic Absences
In certain Bravais lattices, specific Bragg peaks may be absent or not observed in the diffraction pattern
- This phenomenon is known as systematic absences and occurs due to the occurrence of destructive interference between the scattered waves from equivalent planes
Systematic absences follow certain restrictions on the Miller indices of the diffracting planes based on the Bravais lattice type
Primitive (P)
- No systematic absences occur, so all possible Bragg peaks are observed
Centered (C)
- Bragg peaks with Miller indices being odd are absent
Body-centered (I)
- Bragg peaks with Miller indices being odd are absent
Face-centered (F) lattice
- Bragg peaks will be absent if the Miller indices h, k, and l are not all odd or all even
- In other words, if all three Miller indices don't have the same parity ( even or odd ), the corresponding Bragg peaks will not be observed
¶ Intensities and Structure Factors
The total scattering factor of a unit cell for a specific (hkl) plane is called the structure factor ( )
- The structure factor is determined by summing over the scattering factor ( ) of all j atoms in the unit cell, while also the phase factors associated with their positions
We can relate the intensities ( ) of the Bragg peaks to the structure factor
- Note that . This is known as Friedel’s Law
Recall that the intensity is related to the Fourier Transform of the electron density distribution within a unit cell
- We can therefore calculate the within the unit cell by calculating the Fourier transform of , summing over all the peaks observed
- But there is a problem, as the amplitude Fhkl depends on its magnitude and the phase ( ) of the scattered wave relative to the origin of the unit cell
- When we take the square root of the intensities of the Bragg peaks, we obtain , but the phase is lost
- However, the phase of each peak is needed to carry out the calculation of the electron density map
- The problem is simplified for centrosymmetric structures, as then the phase can only be or