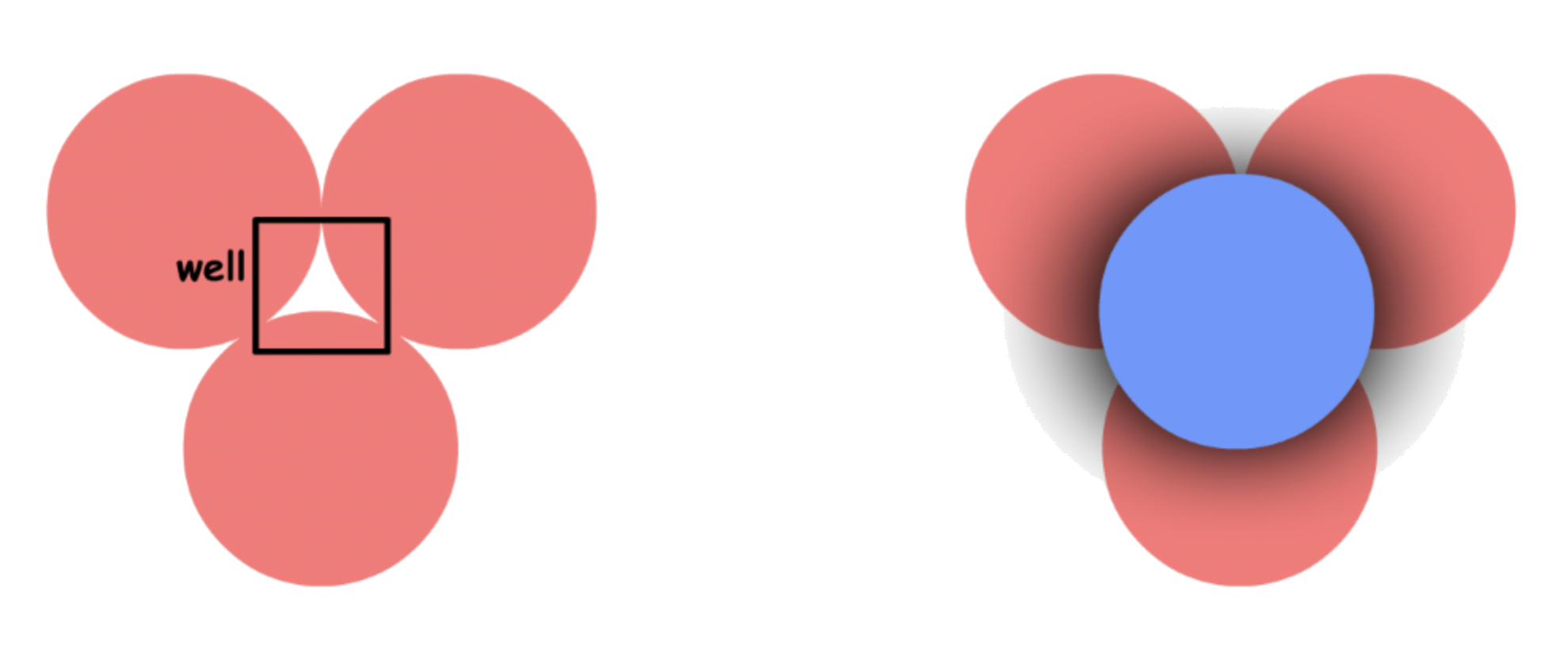¶ Describing a Crystaline Structure
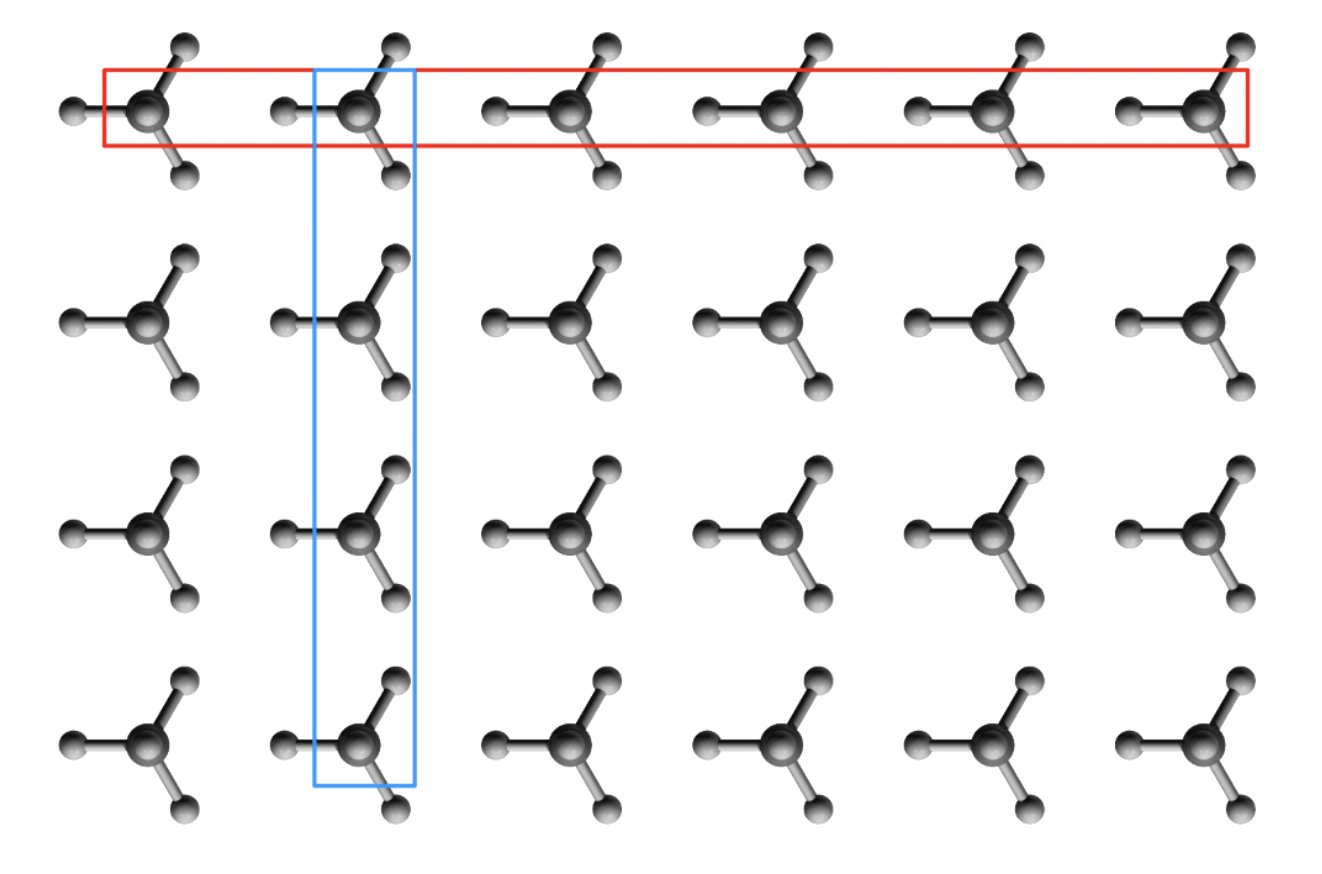
A crystalline structure is in essence a regular array of objects in space
- All the particles are oriented the same way and repeat in all three dimensions
- All the particles are equidistance from each other
Due to the arrangement, there will be layers of atoms in the crystalline structure
- An atom at a particular position in one molecule is in the same position for the next one and the next one and so on
¶ Lattice and Motif
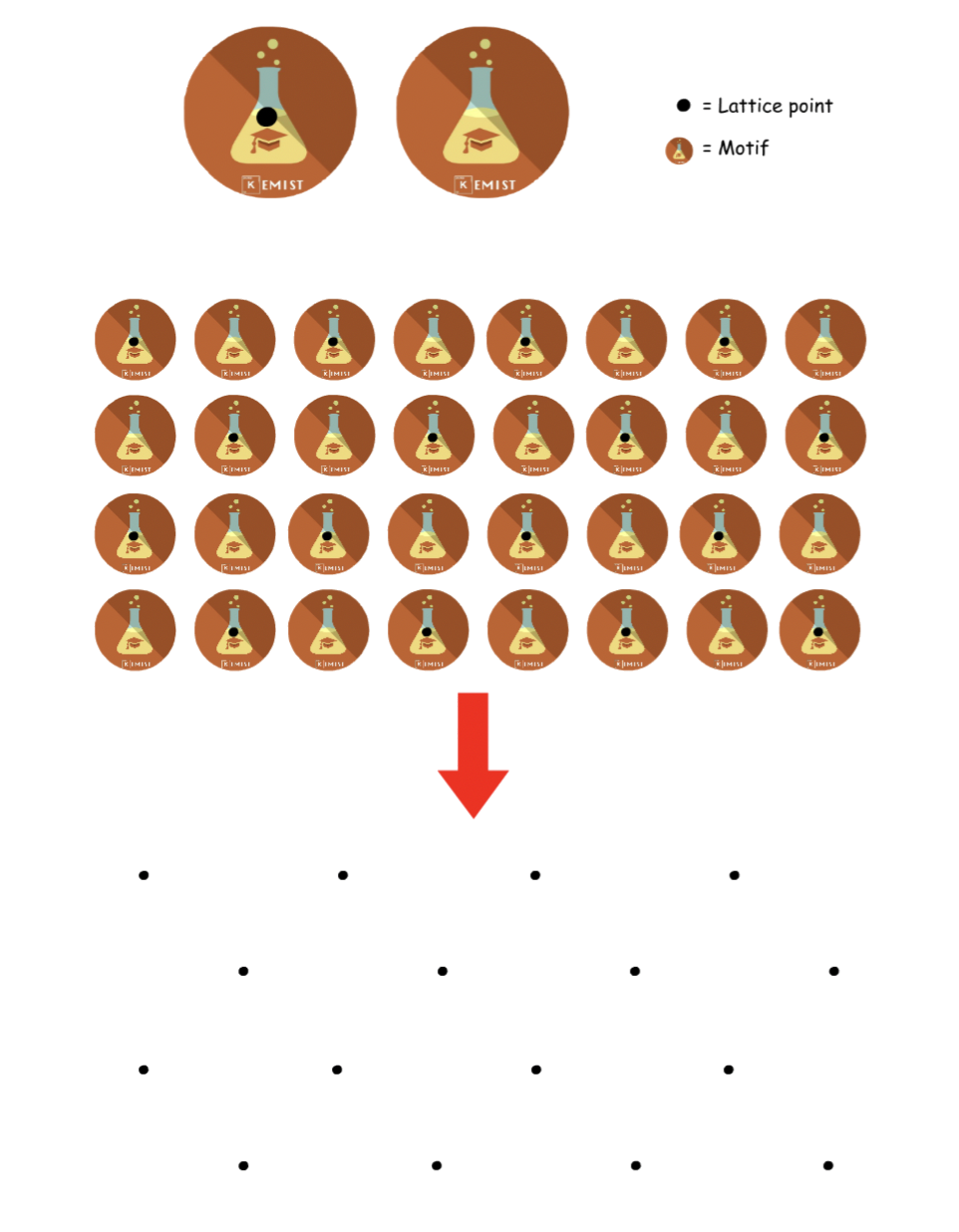
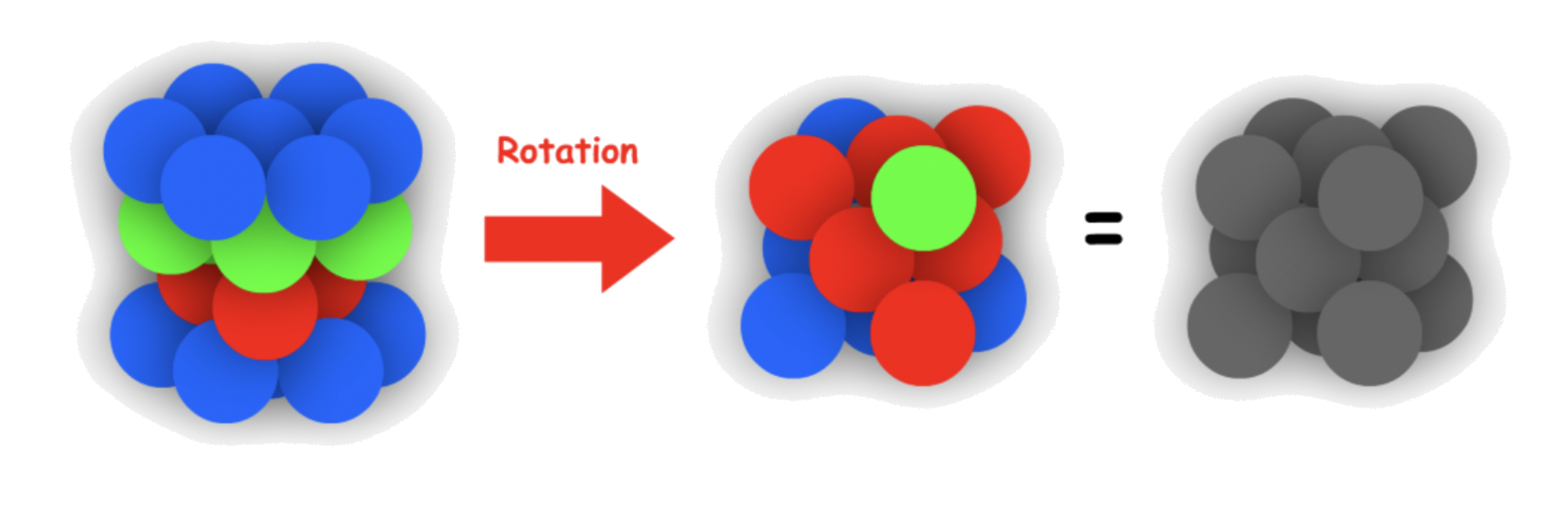
Crystaline structures can be described using lattices and motifs
- Lattice: A set of imaginary identical points in space
- Motif: Real objects that are associated to lattices point
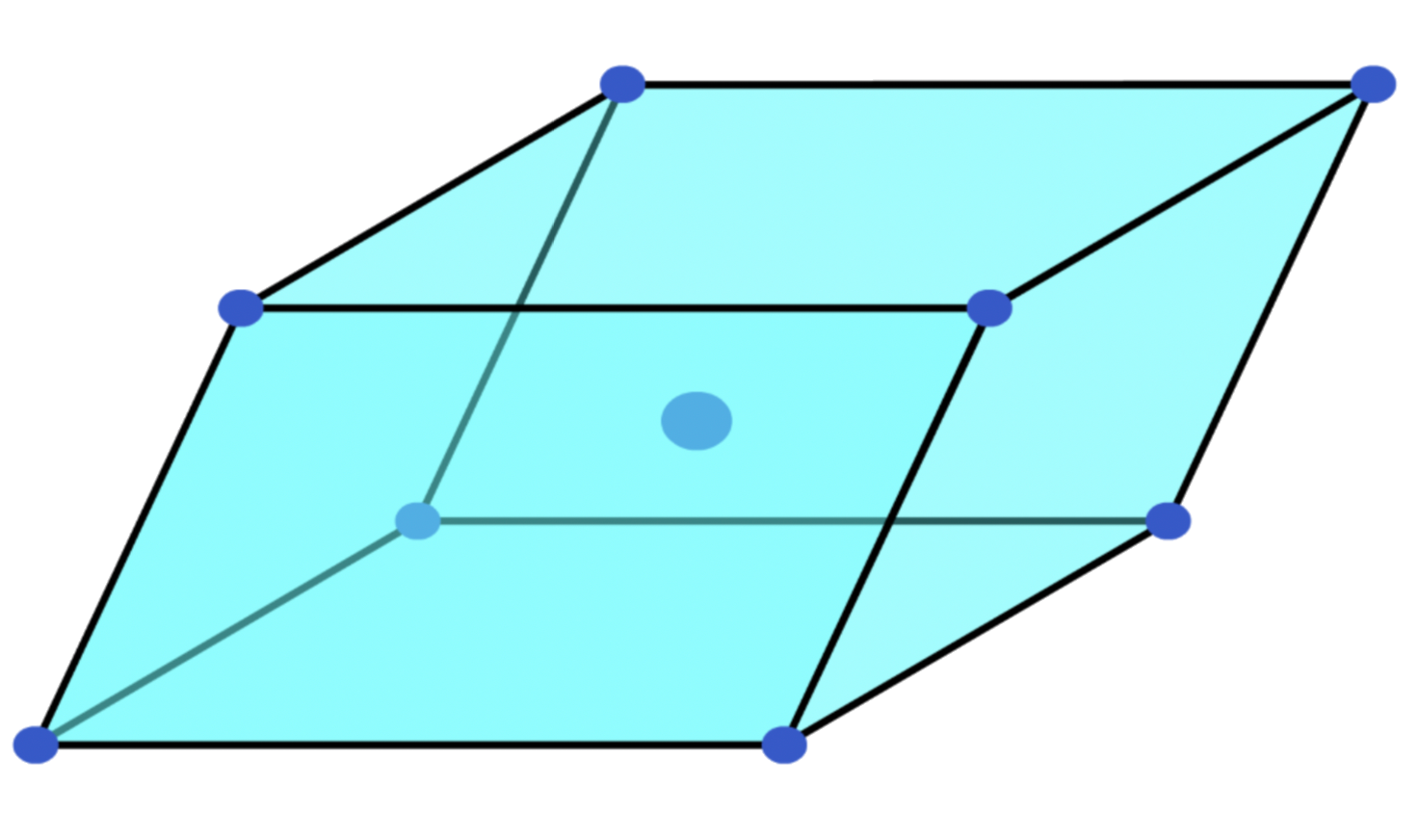
Say we have a structure like the one above, we can assign a lattice point to the motif
- The lattice point can be in any position in space ( does not necessarily have to be on the motif )
- Every lattice point should have the same relative position to the motif
- Once every motif has been assigned with a lattice point, the motif can be removed from the diagram
The motif does not have to be the smallest repeating unit
- The number of lattice points will not decrease as there an infinite number of them
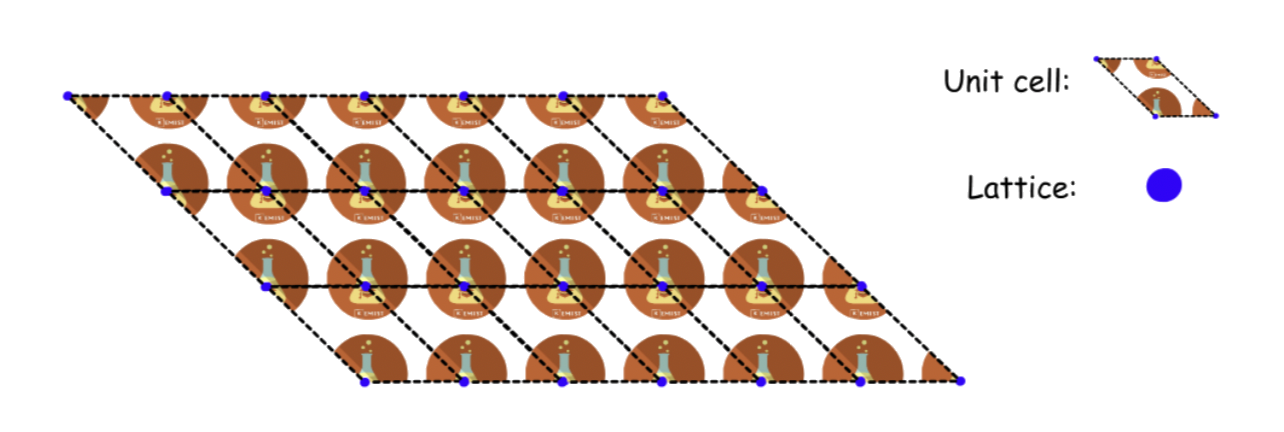
¶ Unit Cells
A unit cell is a block of space, when repeated and packed together will reproduce the crystal structure
- The corners of a unit cell are identical points in space, aka, lattice points
Unit cells cannot undergo rotations, so they cannot be in shapes that cannot stack upon each other without rotating
Unit cells do not have to be the smallest repeating units
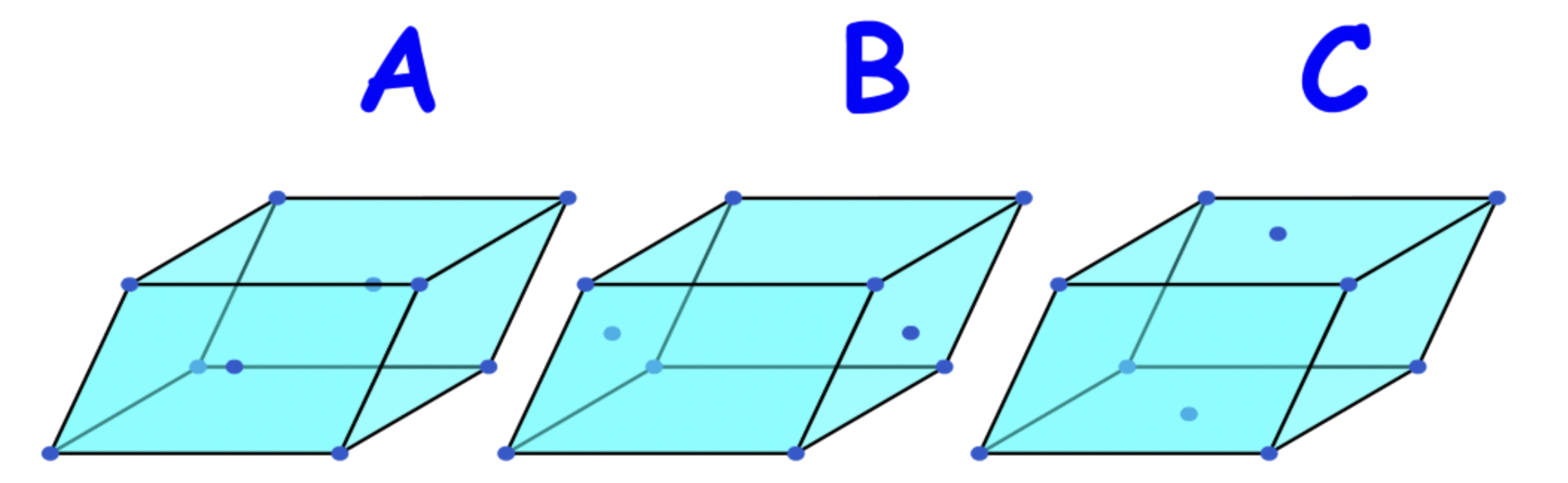
Primitive unit cells
- Lattice points are only present at the corners of the unit cell
Smallest repeating units- They can come in different shapes
Non-primitive unit cells
- Apart from having lattice points at the corner of the unit cells, there are additional lattice points within or at the edge of the cell
- Not the smallest repeating units
- They can come in different shapes
¶ 3D Unit Cells
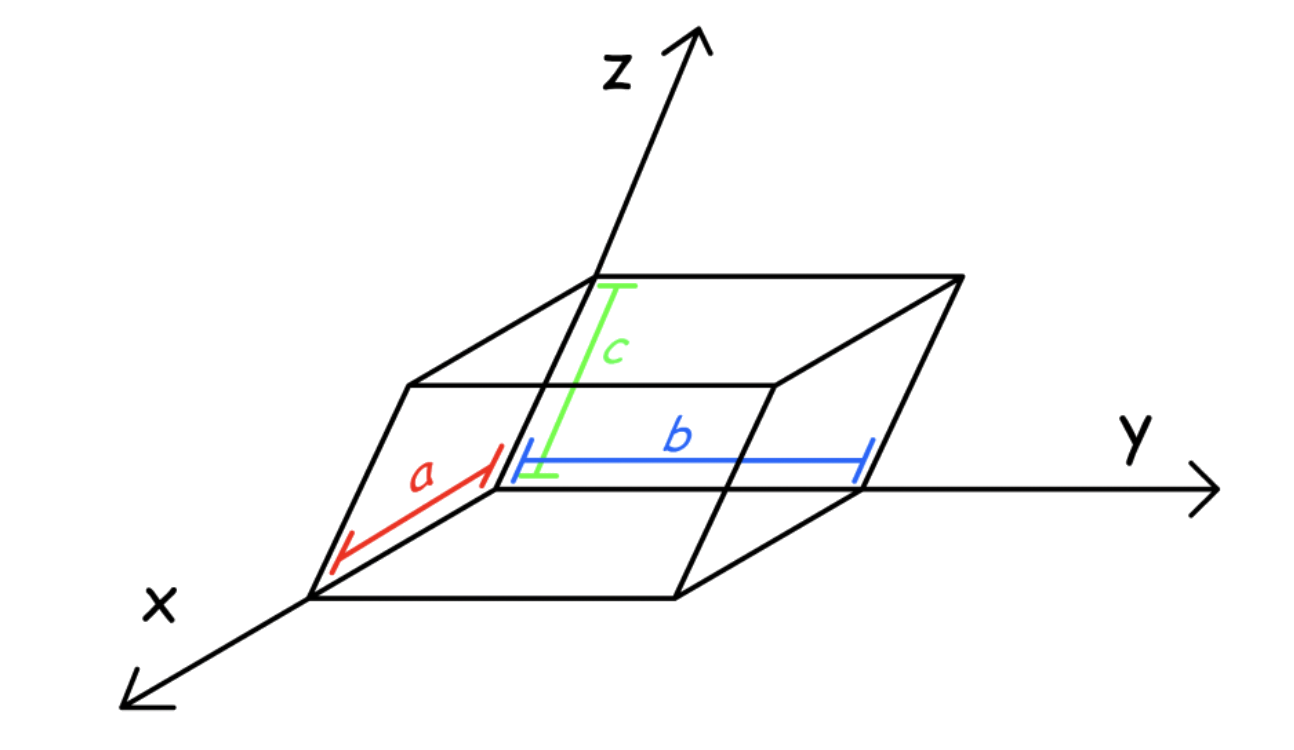
3D unit cells must be parallelepiped
- They must have Identical corners, identical parallel edges and identical parallel faces
3D unit cells parameter
A unit cell is characterized by six parameters
- The three edges (, and )
- The angles between the edges ( , and )
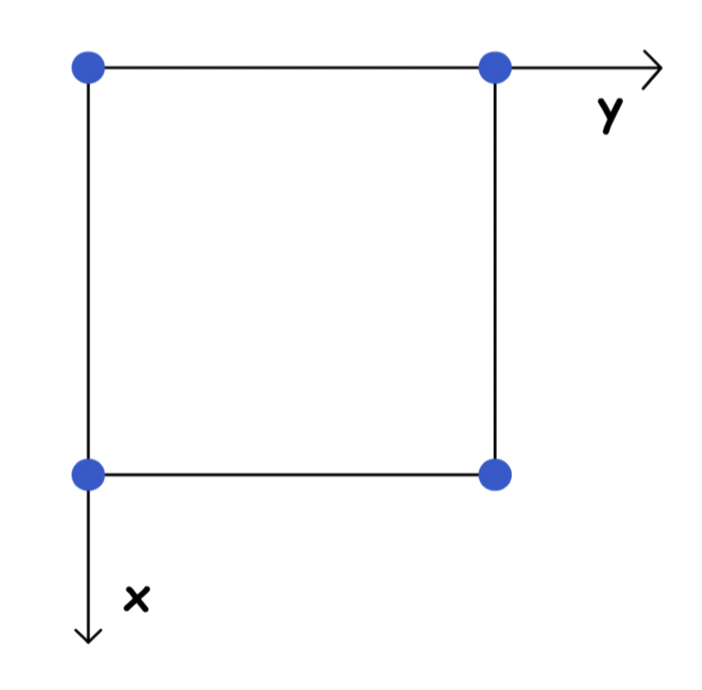
Dimensions along the edges of a unit cell is represented by x, y and z
- These axes may or may not be perpendicular to each other
The parallel sides are of the same length: a, b, c
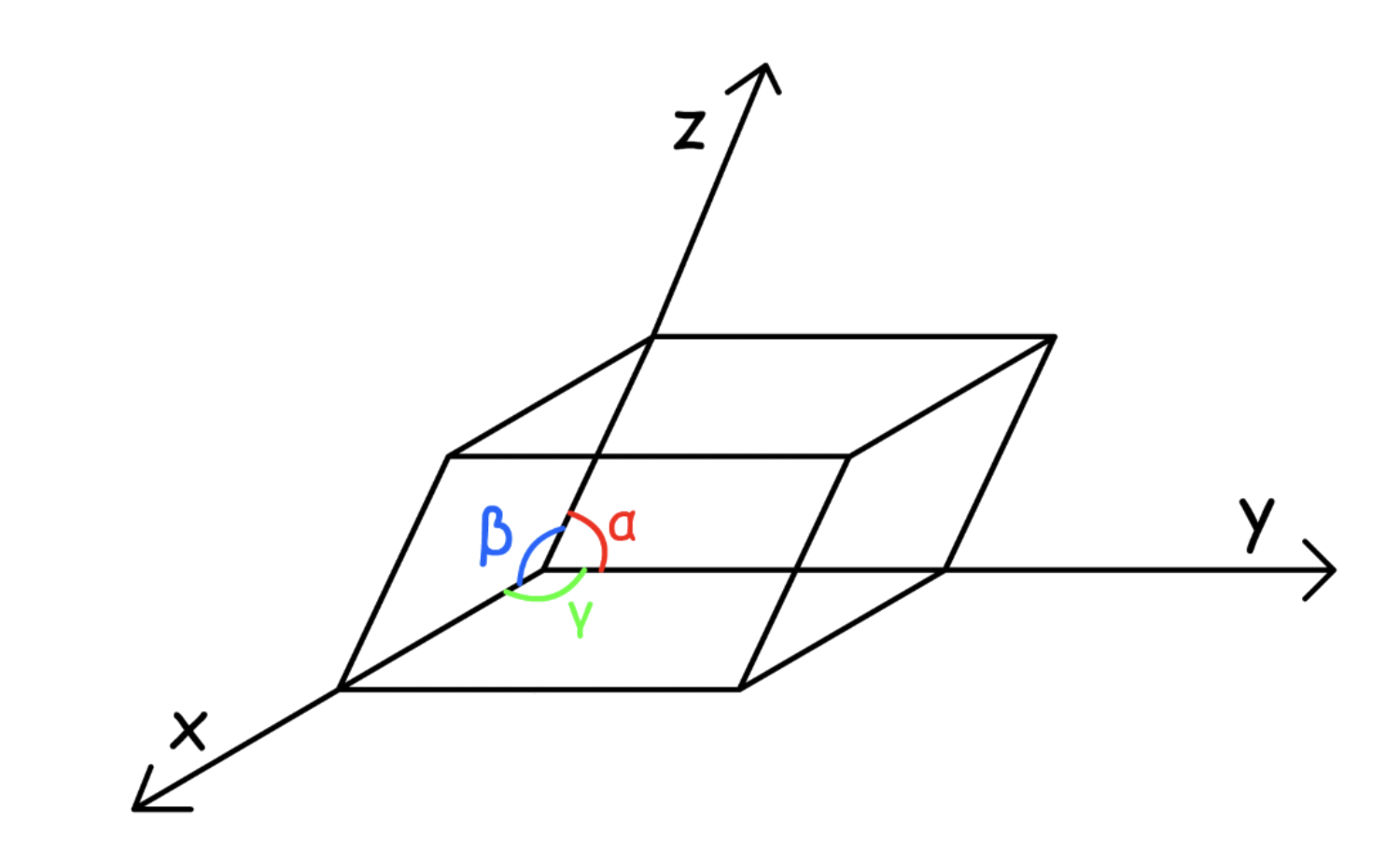
The angles at the origin are called α, β, γ ( opposite a, b and c )
- The angle between b and c is represented by α, between a and c by β and between a and b by γ
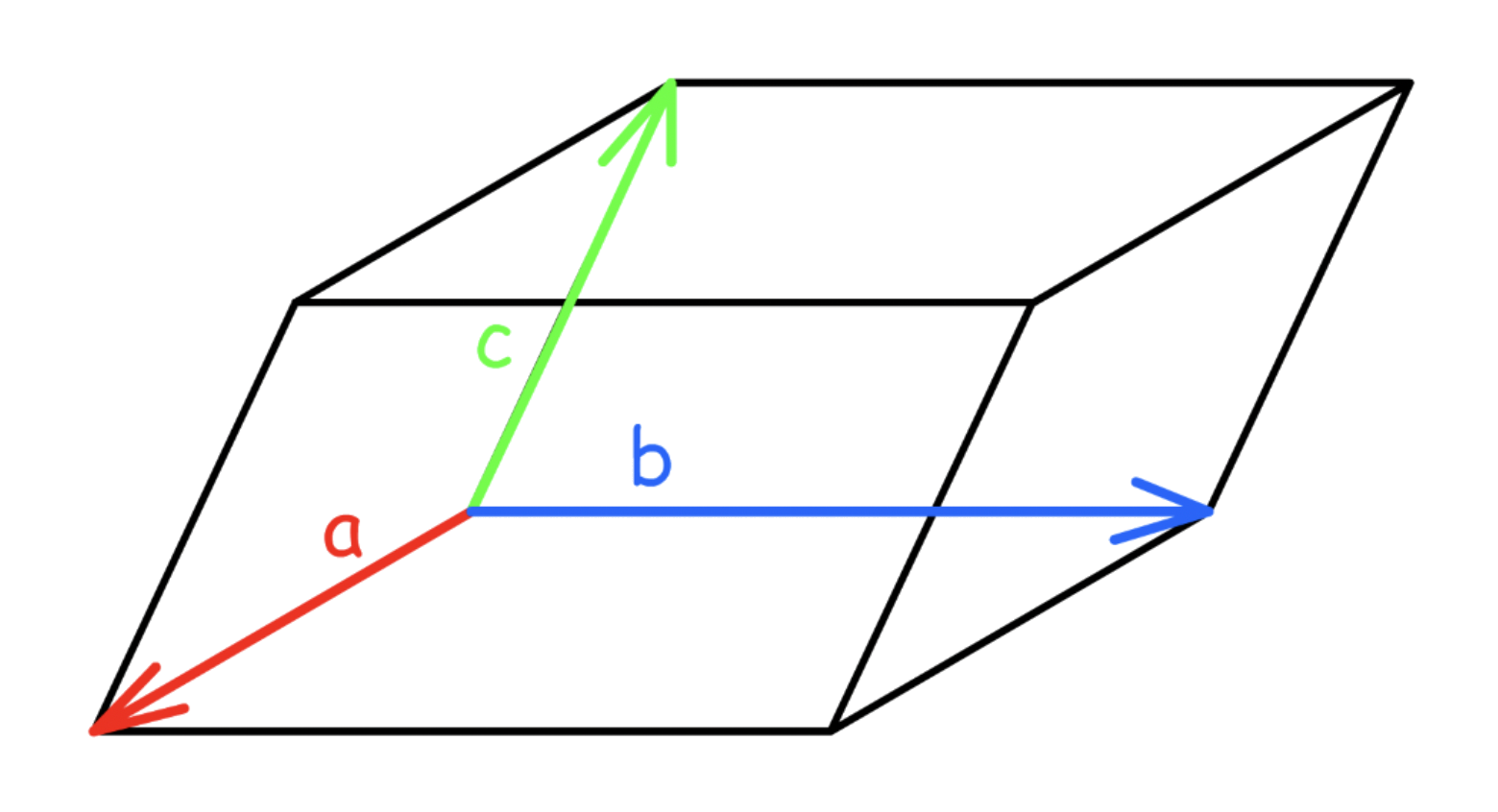
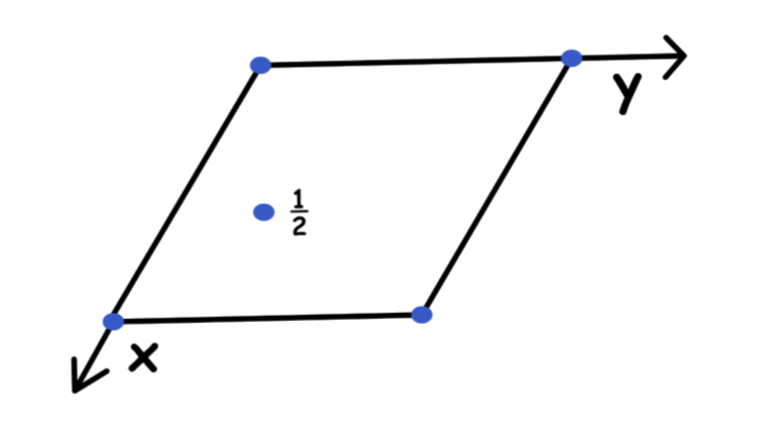
To encapsulate both ideas ( length and angle ), we use unit cell vectors
- Unit cell vectors give you information about magnitude ( distance ) and vectors
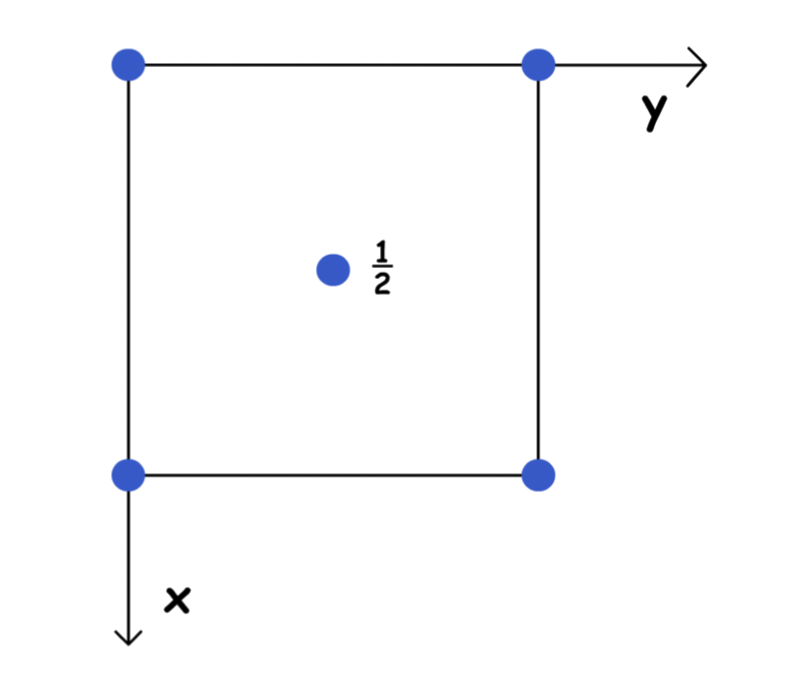
We can describe any point within the unit cell using the fraction of the vectors a, b, c
- We always start from the origin ( 0, 0, 0 )
Unit cells are not in isolation, rather they are stacked together in all three dimensions. Hence, the lattice points lying on the corners, edges or faces of a unit cells are shared between unit cells
- These lattice points will have equivalent counterparts within the cell, so only the set of coordinates with the smallest value is shown
- To find the crystal structure, simply apply the vector coordinates to EVERY lattice points in the cell and any consider the positions of structures drawn outside the cell and reapply it back to the original cell
Counting Objects in the Unit Cell
Objects at the corner of the unit cell
- Shared between 8 unit cells
- Count as
Objects on the edge of the unit cell
- Shared between 4 unit cells
- Count as
Objects on the face of the unit cell
- Shared between 2 unit cells
- Count as
Objects completely within the unit cell
- Shared between 1 unit cells
- Count as
Types of unit cells
There are 4 types of unit cells:
- Primitive, Body-centered & Face-centered, Side-Centered
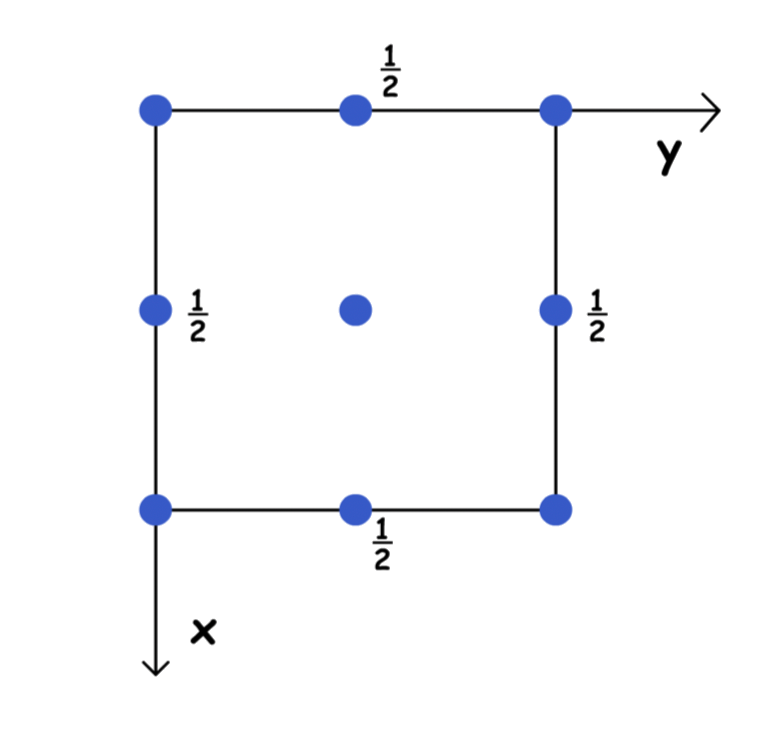
Primitive unit cells ( P )
- Lattice points at corners only
- Lattice point at
Face-centered unit cells ( F )
- Lattice points at corners and all face centers
- Lattice point at , , and
Body-centered unit cells ( I )
- Lattice points at corners and the center of the unit cell
Lattice point at ,Side-centered unit cells ( A / B / C )
- Lattice points at corners and the center two parallel faces
- There are three types of side-centered unit cells: A, B & C
- For A, Lattice point at ,
- For B, Lattice point at ,
- For C, Lattice point at ,
¶ Packing of Spheres
We can consider atoms/ ions as hard spheres, and that their structures can be described by how those spheres are arranged
- The packing of spheres can either be categories as close-packing or non-close packing
We define two important parameters to characterize each packing method
- Atom Coordination: The number and geometric arrangement of nearest atom
- Packing efficiency: The percentage of volume of the unit cell occupied by the atoms
¶ Close Packing
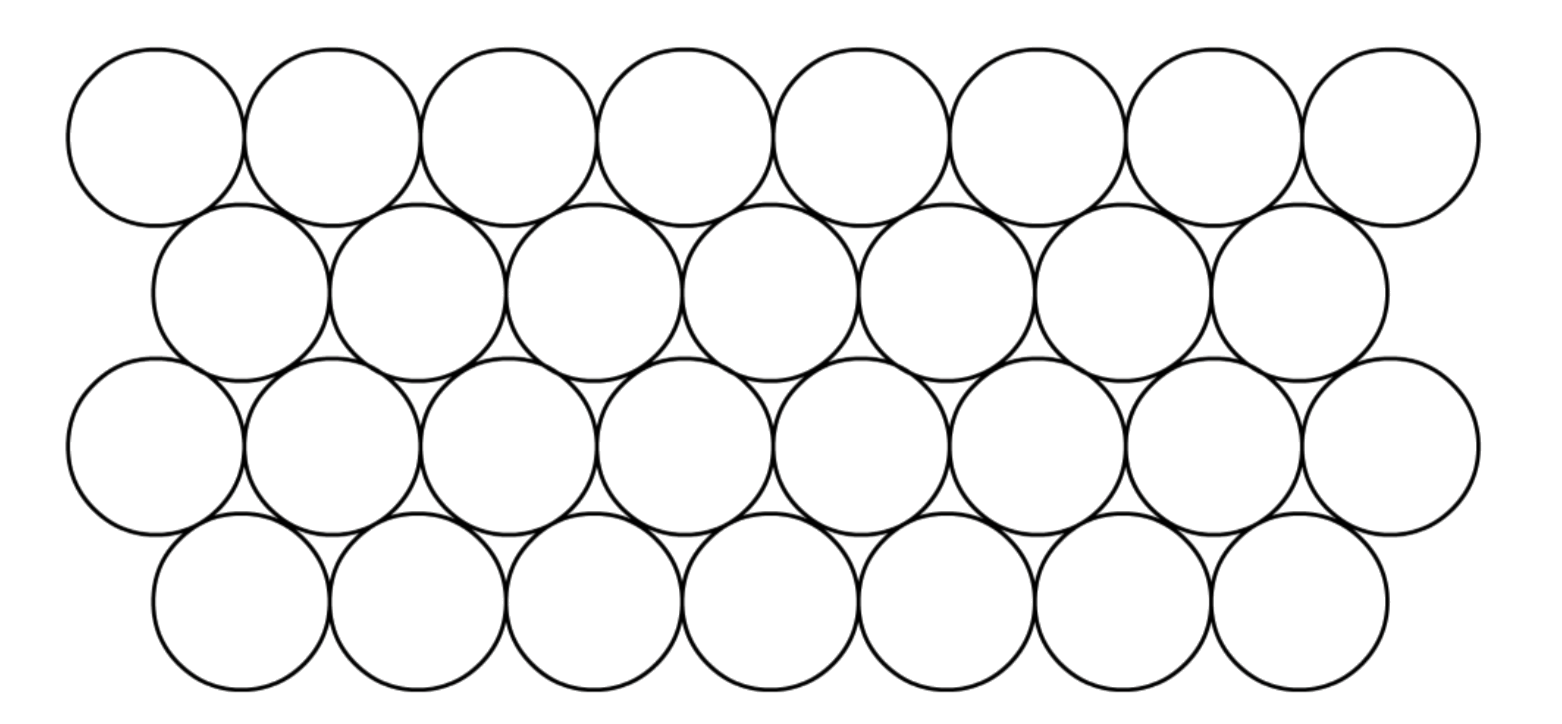
Close-packing is the most efficient form of space-filling arrangement for spheres
- Every layer of "sphere" is slightly offset with respect to the adjacent levels
- It has a packing efficiency of 74%
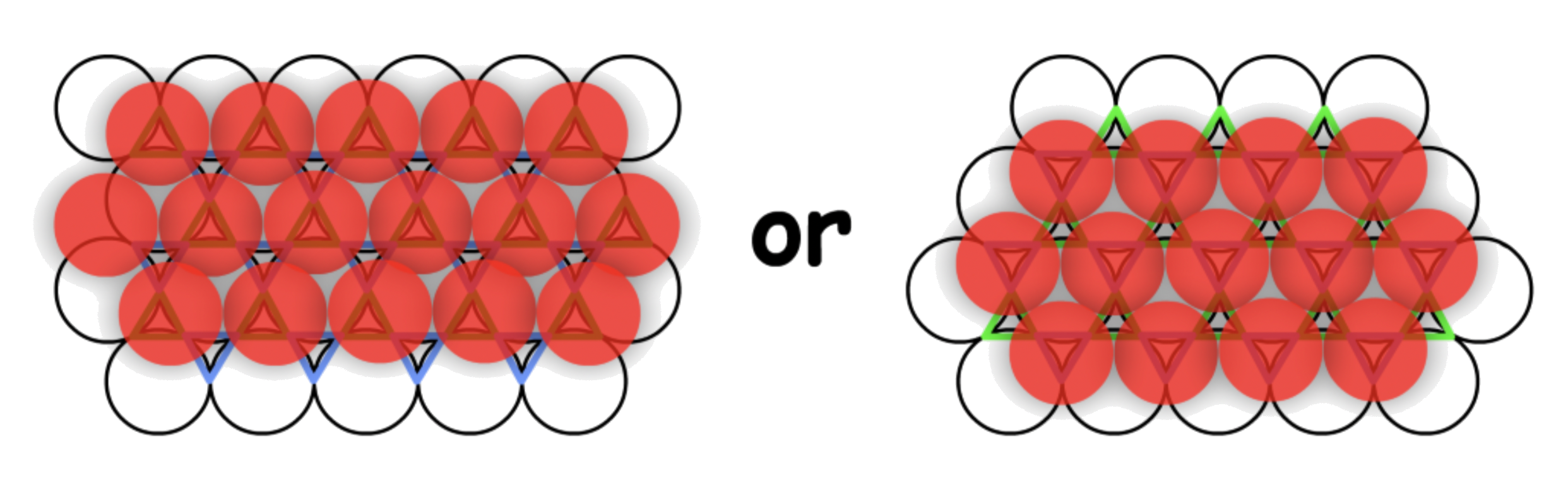
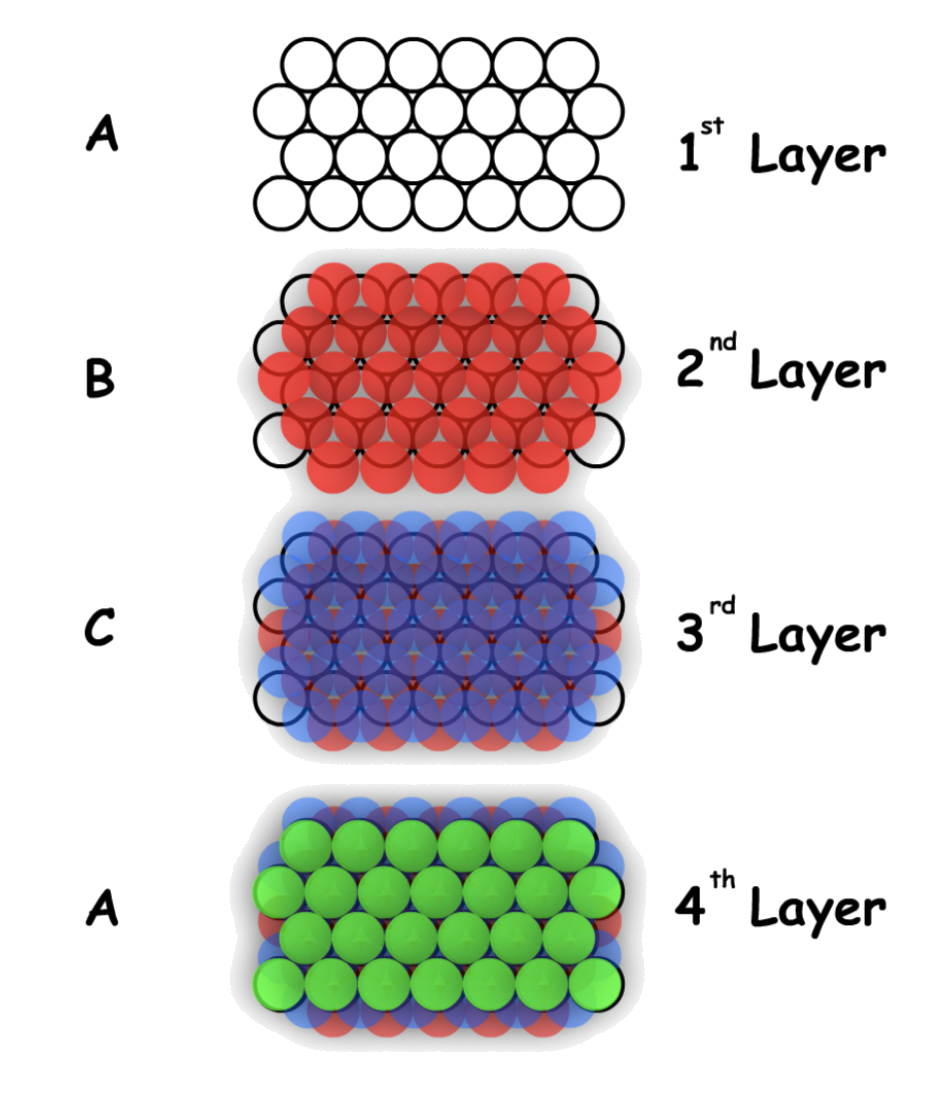
To construct a 3D close-packing structure, we stack the planes on top of each other
- However we do not just put it on top of the original plane directly, we will slide the layer in a fashion that the sphere on top will fit inside the well created by the bottom three spheres
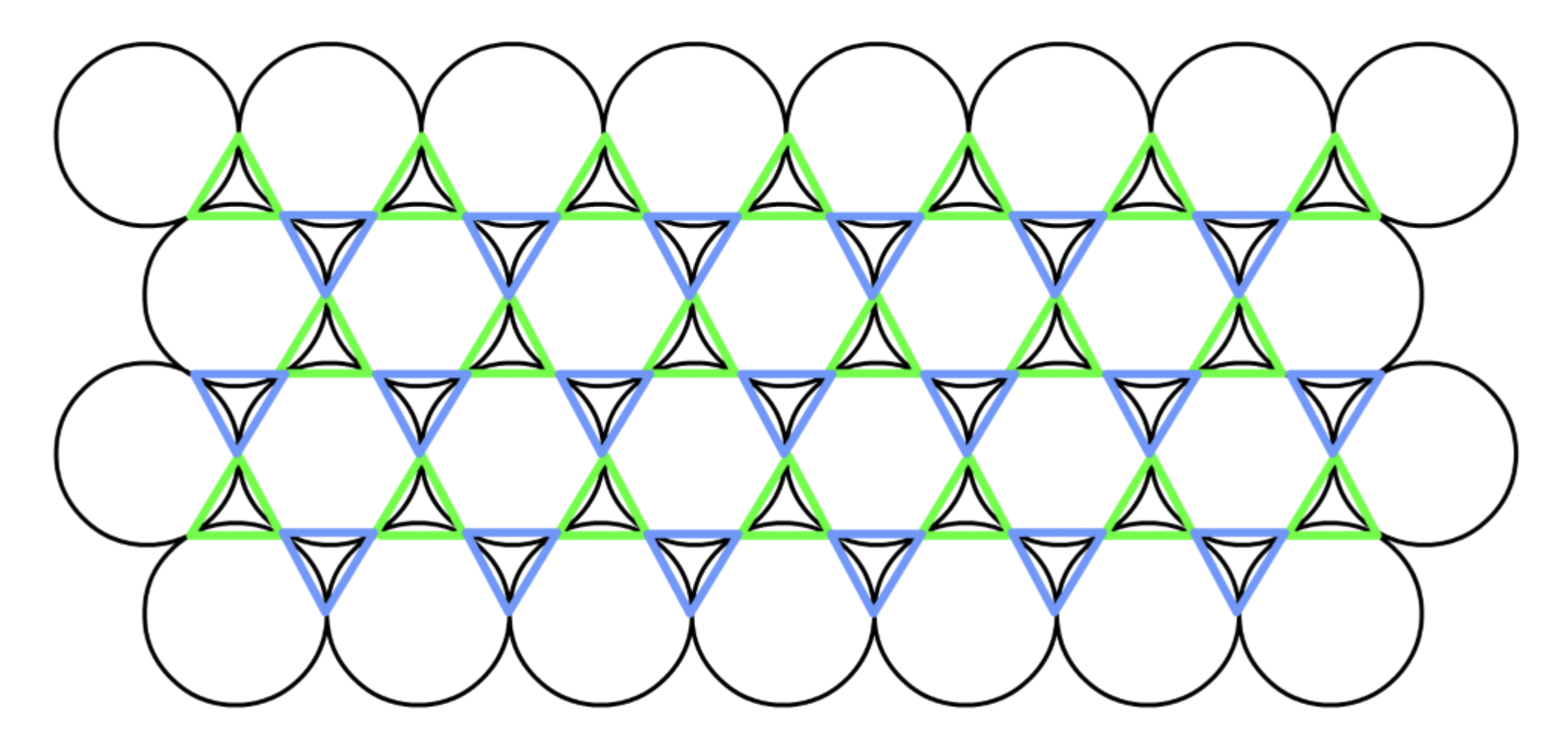
- For any plane of closed-pack spheres, there are two sets of wells
- Any plane can only stack on one sets of wells
There are two types of close-packing
- Hexagonal close-packing and cubic close-packing
- They only differ in regards to how each layer is stacked on top of one another
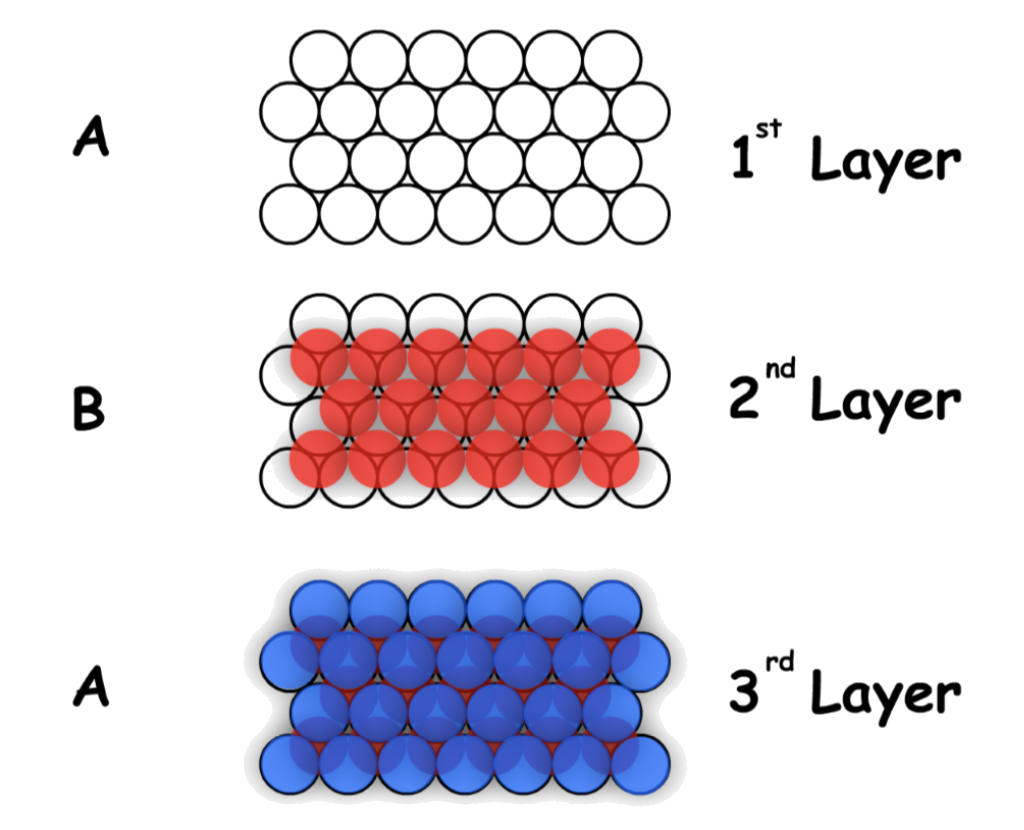
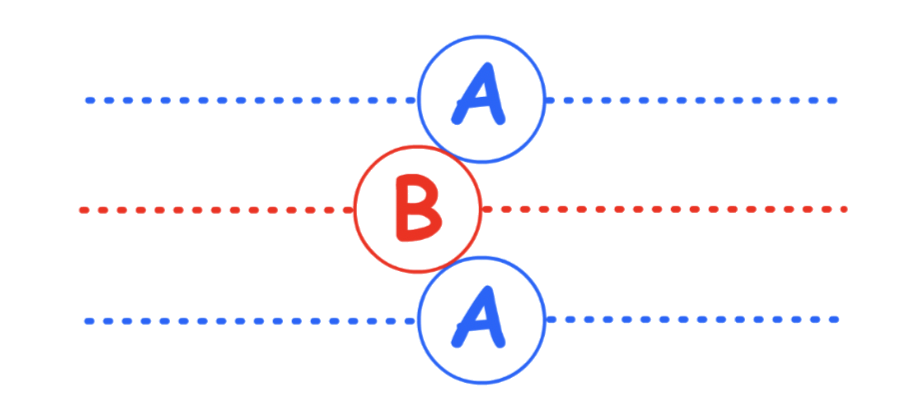
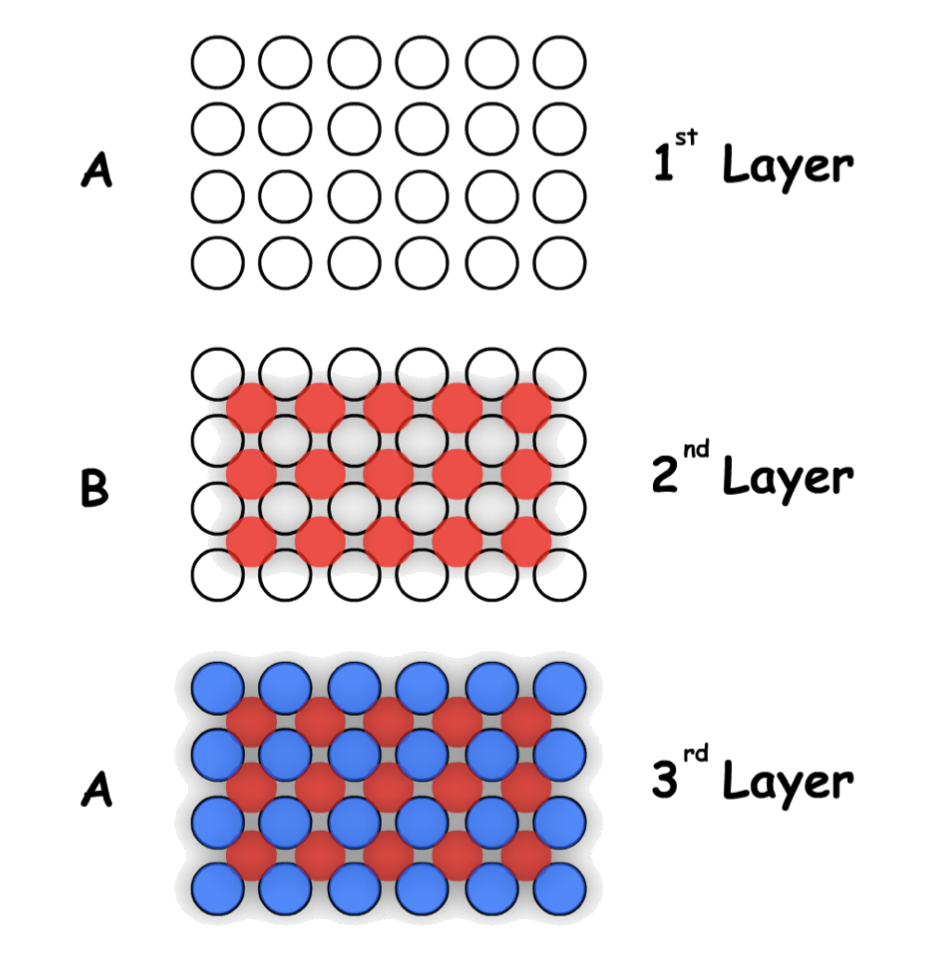
Hexagonal Close-Packing (HCP)
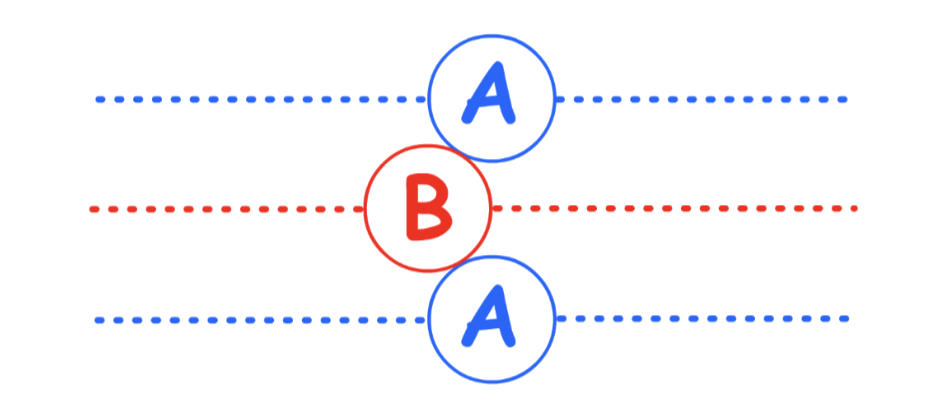
Hexagonal Close-Packing is defined by its "ABA" layers
- There are two different layers in the hexagonal close-packing, each slightly offset with respect to each other
- In three dimension :
The arrangement of atom/ ion can be represented using a unit cell
- ;
- Atom Coordination: 12
- Packing Efficiency: 74%
Cubic Close Packed ( CCP )
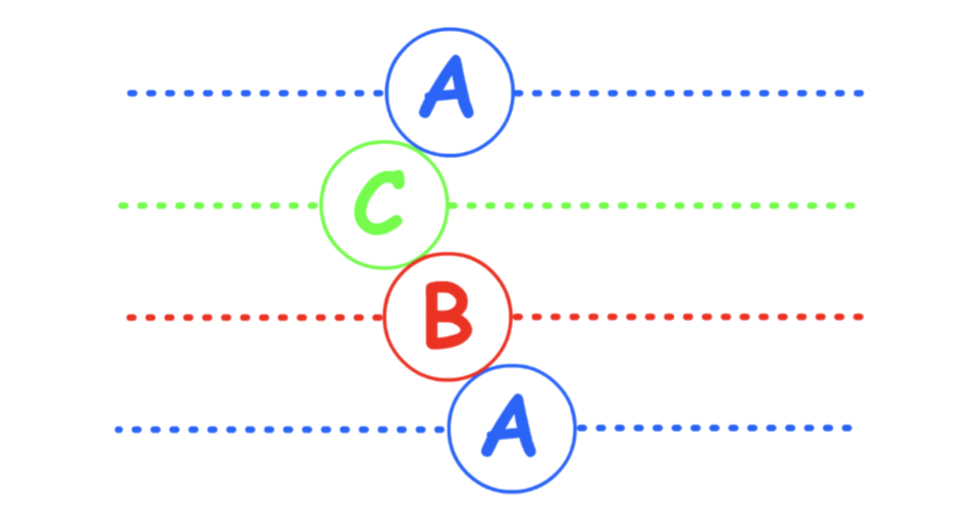
Cubic Close Packed is defined by its "ABCA" layers
- The second layer will stack on top of the first layer in one set of the wells, while the third layer will stack on top of the second layer in a set of wells that is mutually owned by the 1st and 2nd layer
- The set of wells that is not used when the 2nd layer is stacked on top of the first one
Using the 3D representation, the structure will appear as a Cubic Face-centered unit cell upon rotation
The arrangement of atom/ ion can be represented using a unit cell
- It is an F type cubic unit cell
- ;
- Atom Coordination: 12
- Packing Efficiency: 74%
¶ Non-Close Packing
Non-close packing is a less efficient form of packing spheres
There are two common types of non-close packing arrangement in metals:
- Body-centered cubic and Primitive cubic
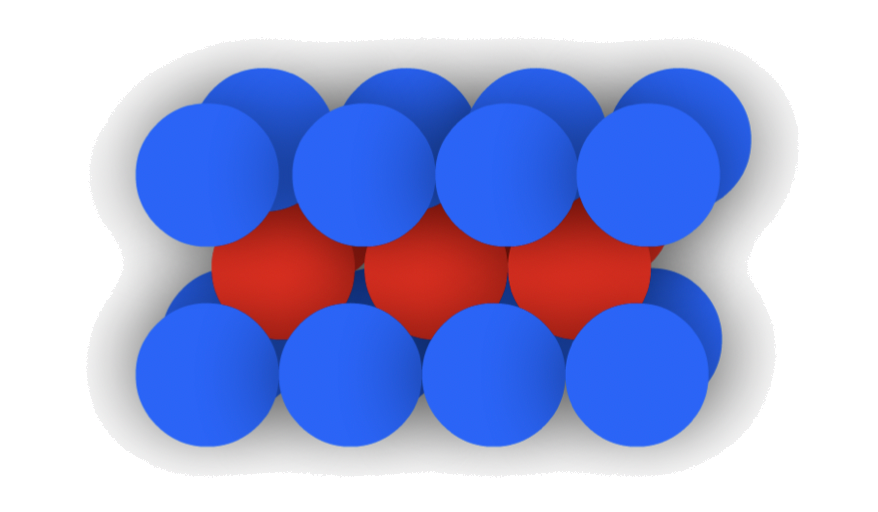
Body-Centered Cubic
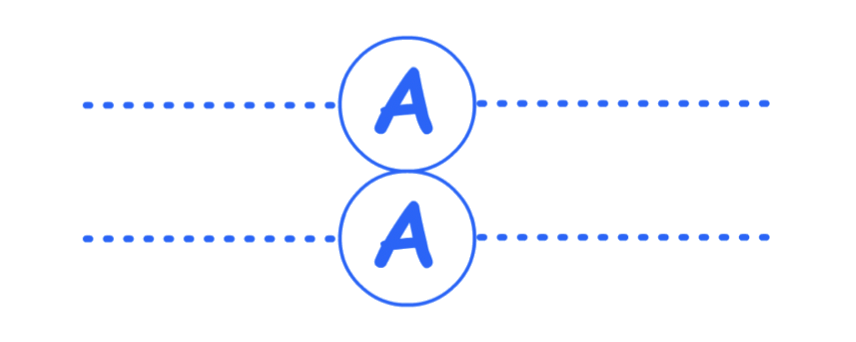
Body-Centered Cubic is defined by its "ABA" layers
- In each layer, the spheres are not touching each other
The arrangement of atom/ ion can be represented using a unit cell
- It is a I type cubic unit cell
- ;
- Atom Coordination: 8
- Packing Efficiency: 68%
Primitive Cubic
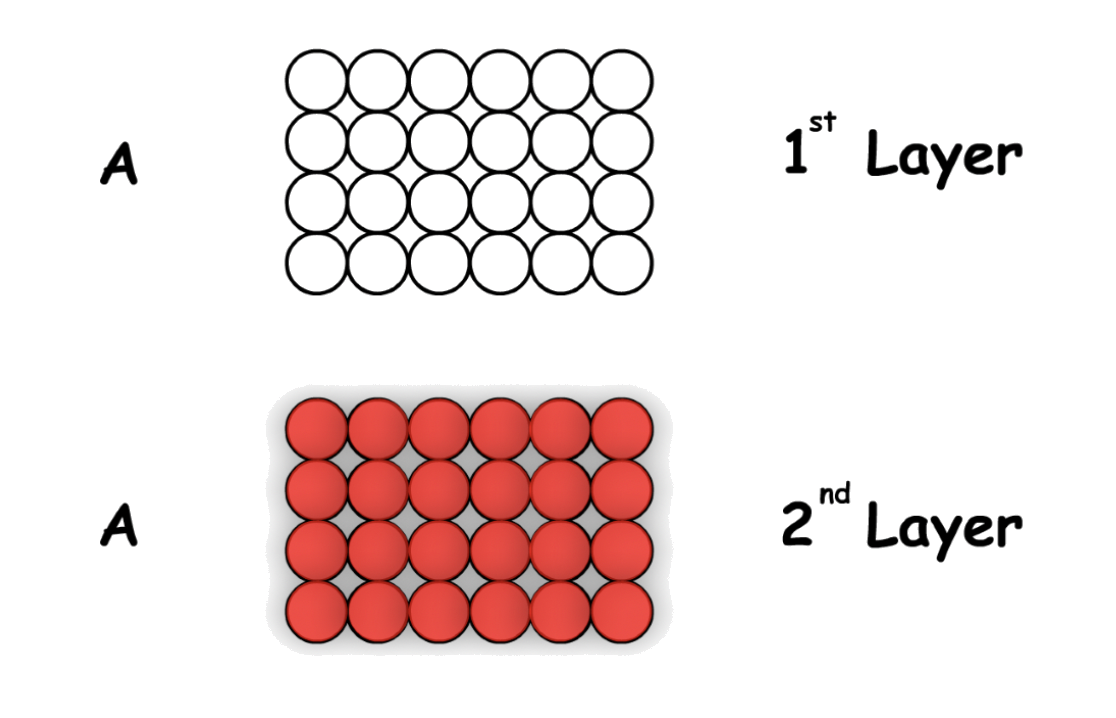
Primitive Cubic is defined by its "AA" layers
- In each layer, the spheres are arranged perpendicularly with respect to their nearest spheres
- The layers of spheres are stacked directly on top of each other
The arrangement of atom/ ion can be represented using a unit cell
- It is a P type cubic unit cell
- ;
- Atom Coordination: 6
- Packing Efficiency: 52%
¶ Holes
The arrangement of spheres will always have cavities between atoms no matter how efficient
- we call these cavities, holes
There are two types of holes:
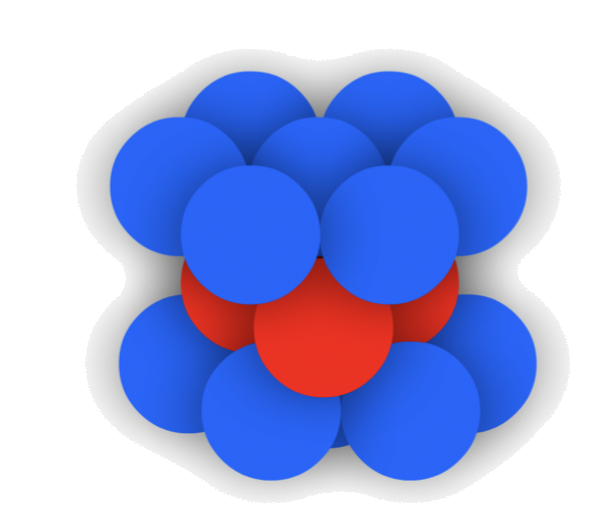
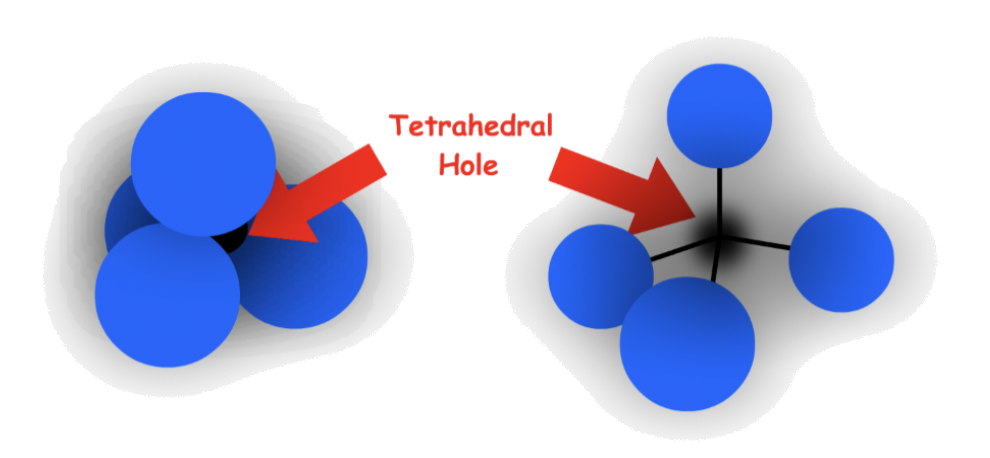
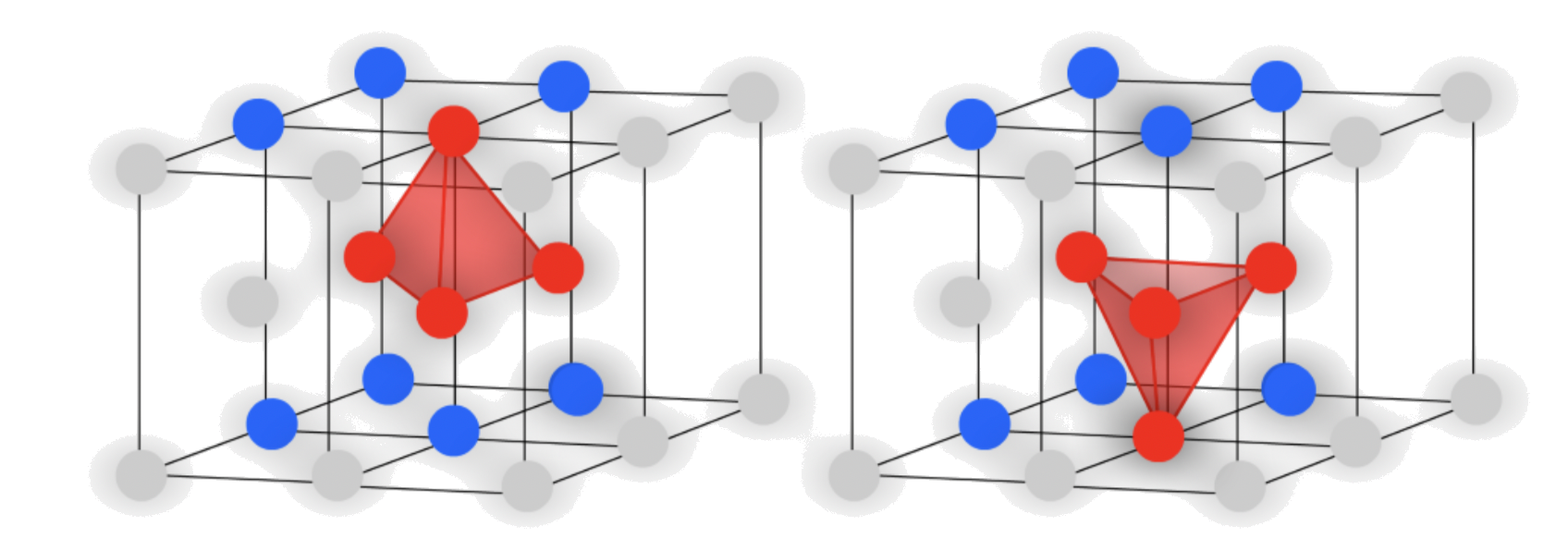
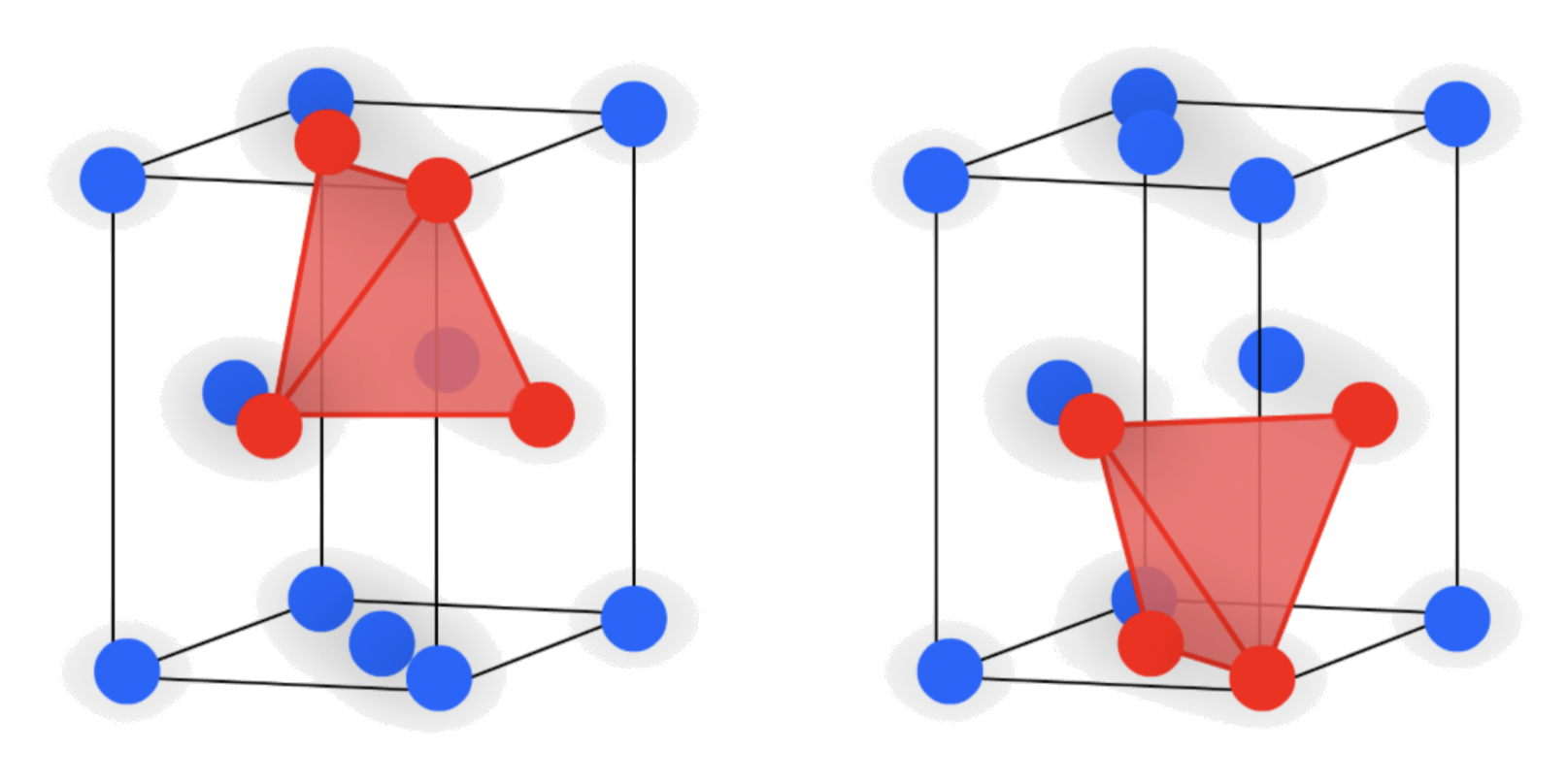
1.Tetrahedral holes
- The cavity is the center of a tetrahedral arrangement of spheres
- 4-coordinate
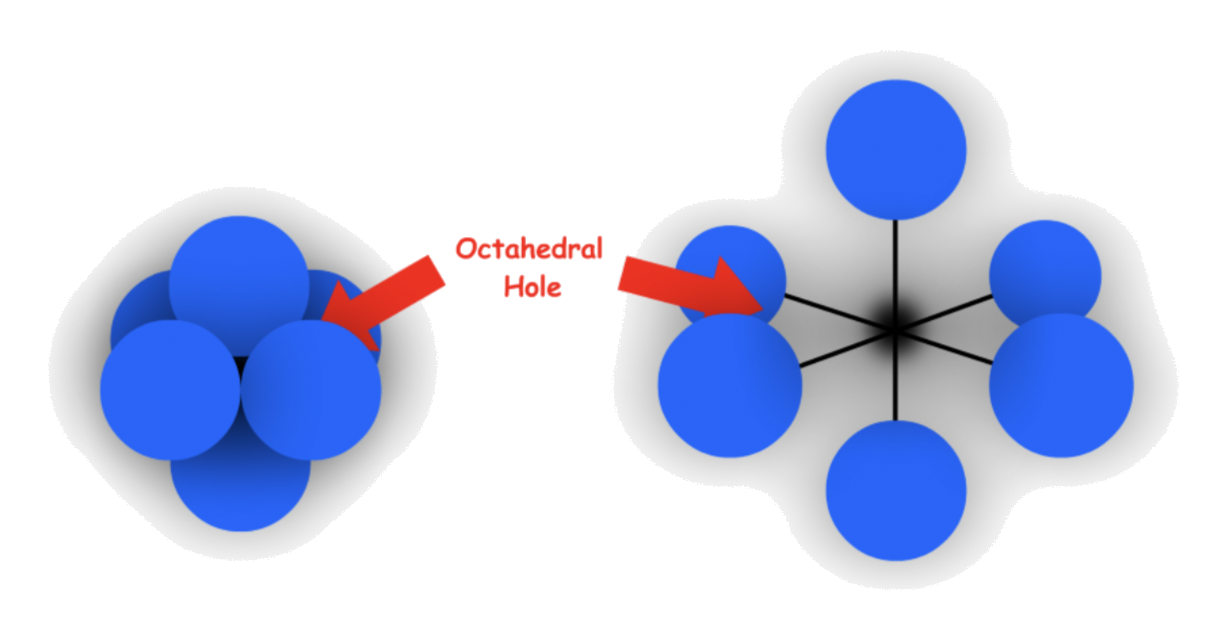
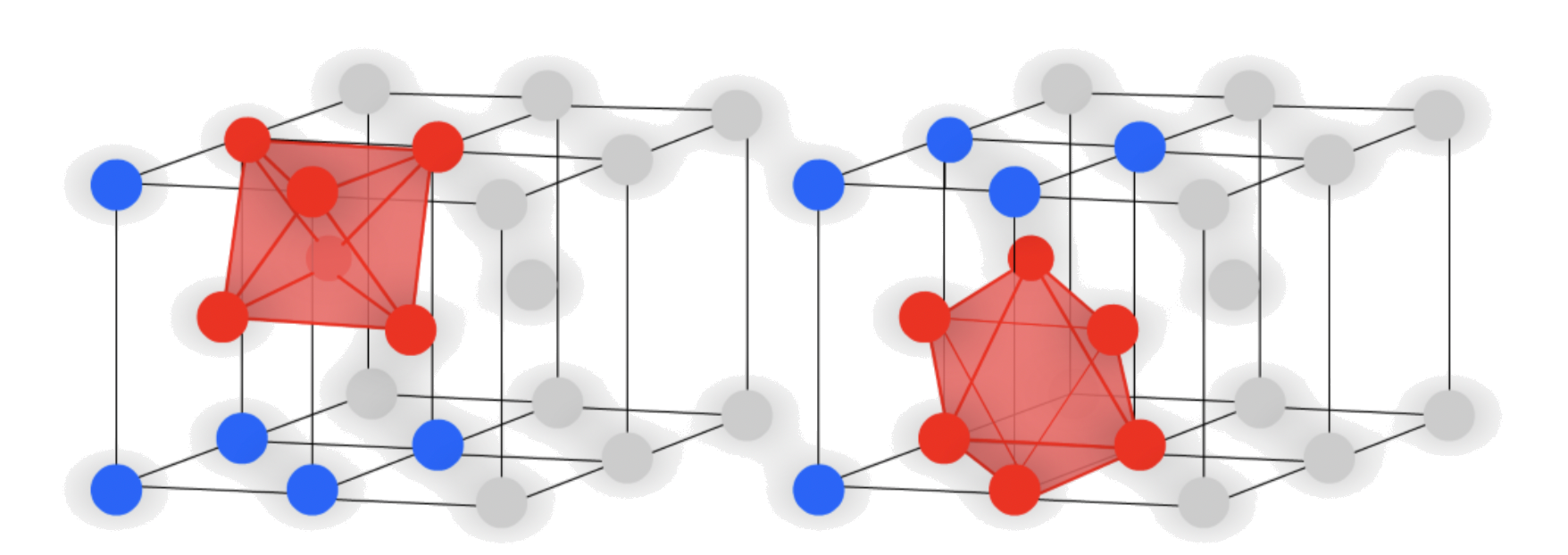
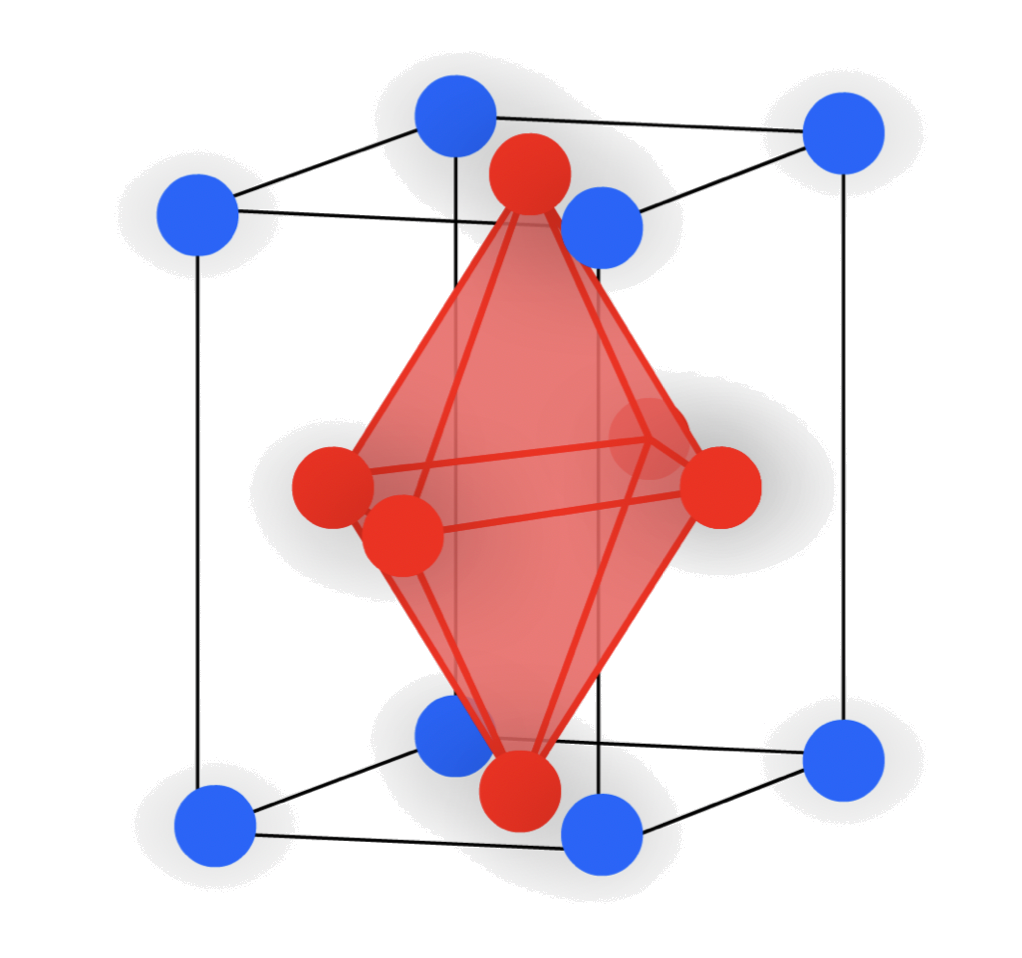
- Octahedral holes
- The cavity is in the center of a octahedral arrangement of spheres
- 6-coordinate
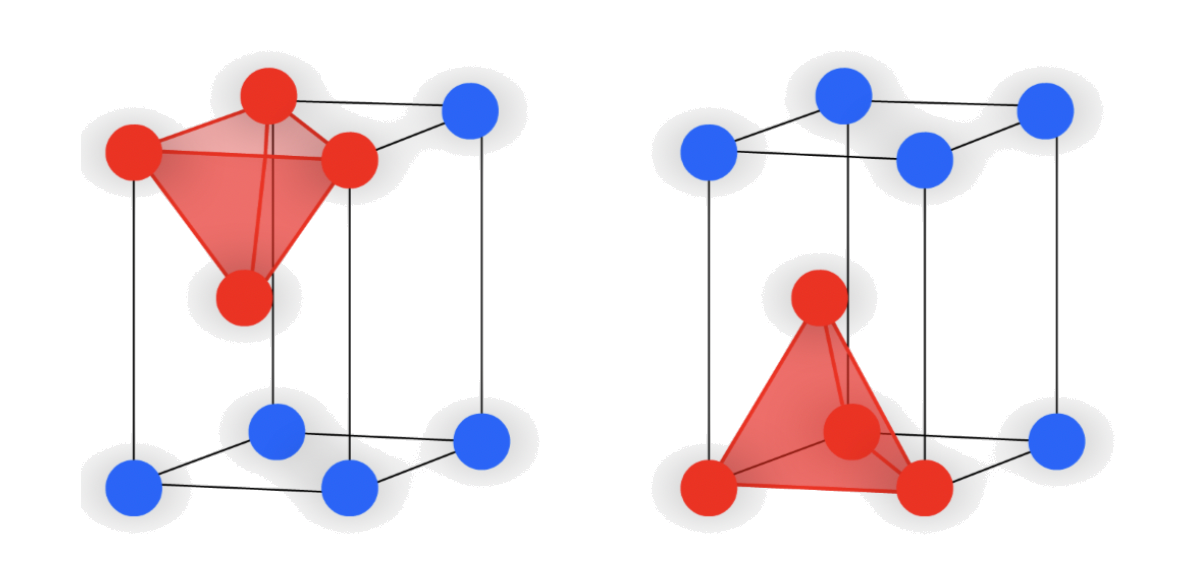
Holes in Hexagonal Close-Pack
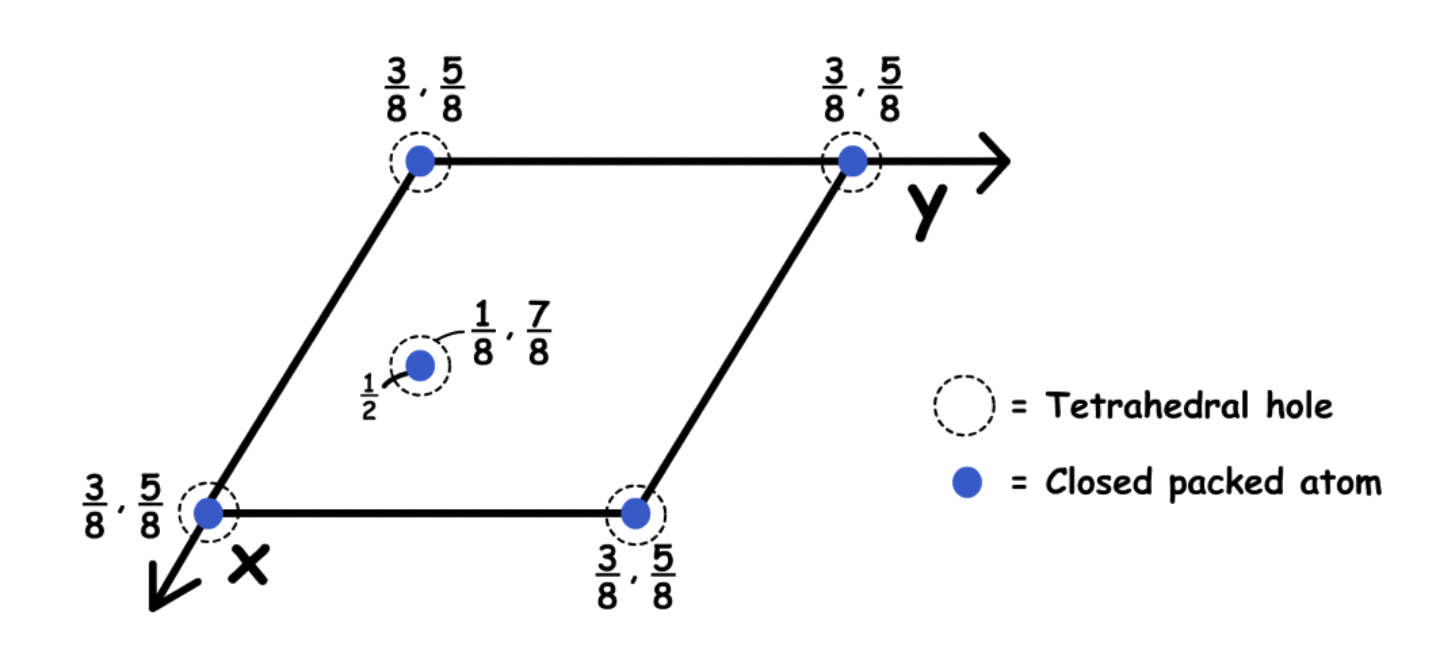
There are two different "types" of tetrahedral holes :
- There are two tetrahedral holes near the atom in the "center"
- There are two tetrahedral hole directly above/ below a corner atom
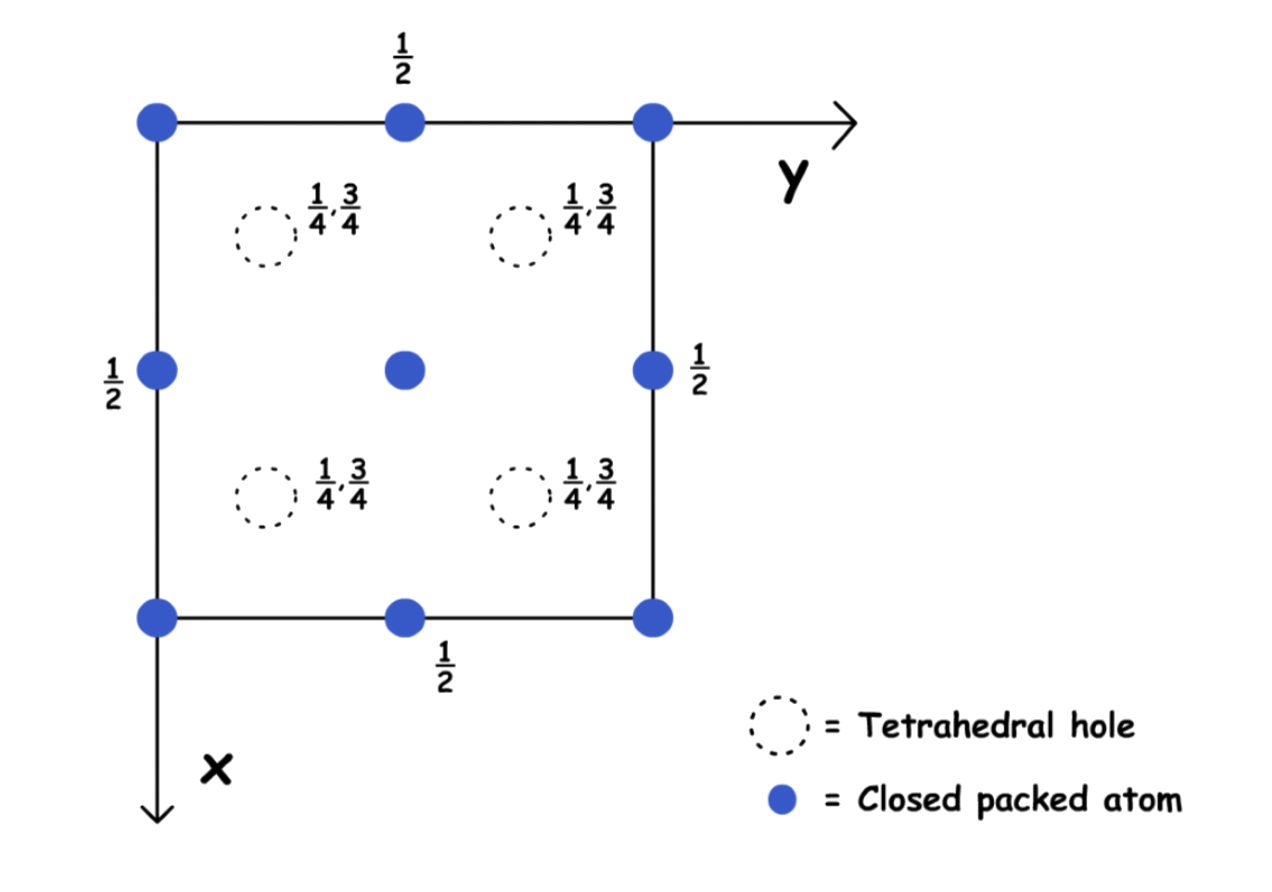
- In unit cell projection :
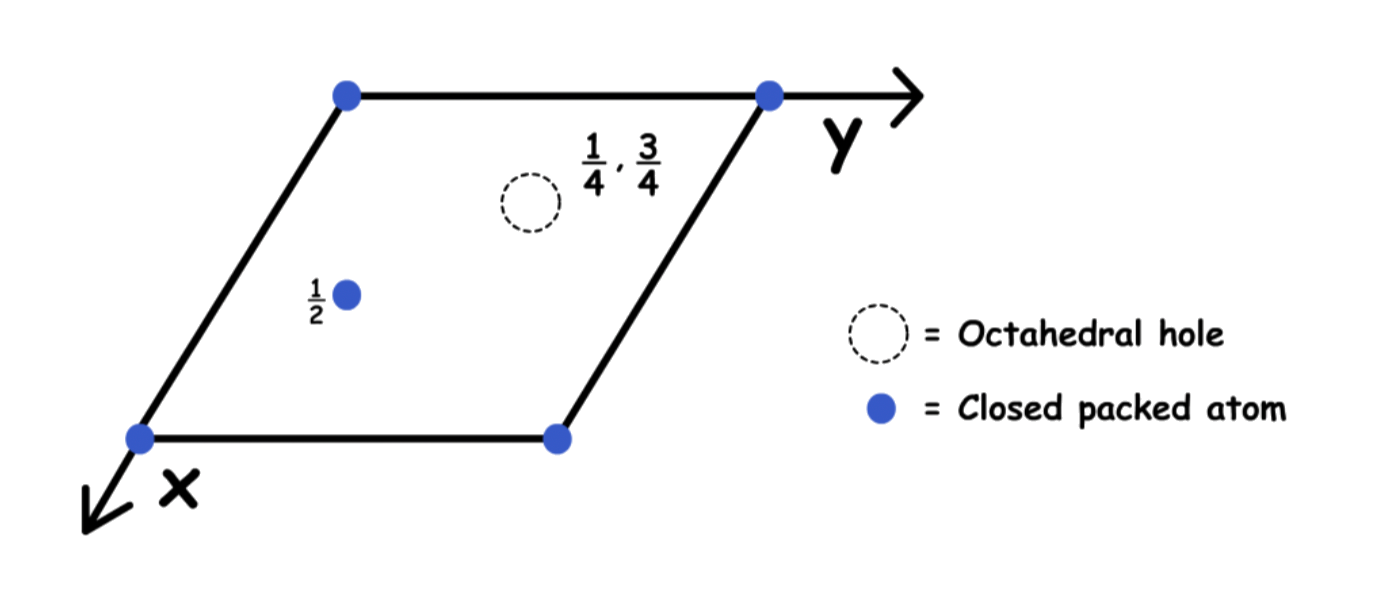
There are two octahedral holes directly above/ below the "vacant area"
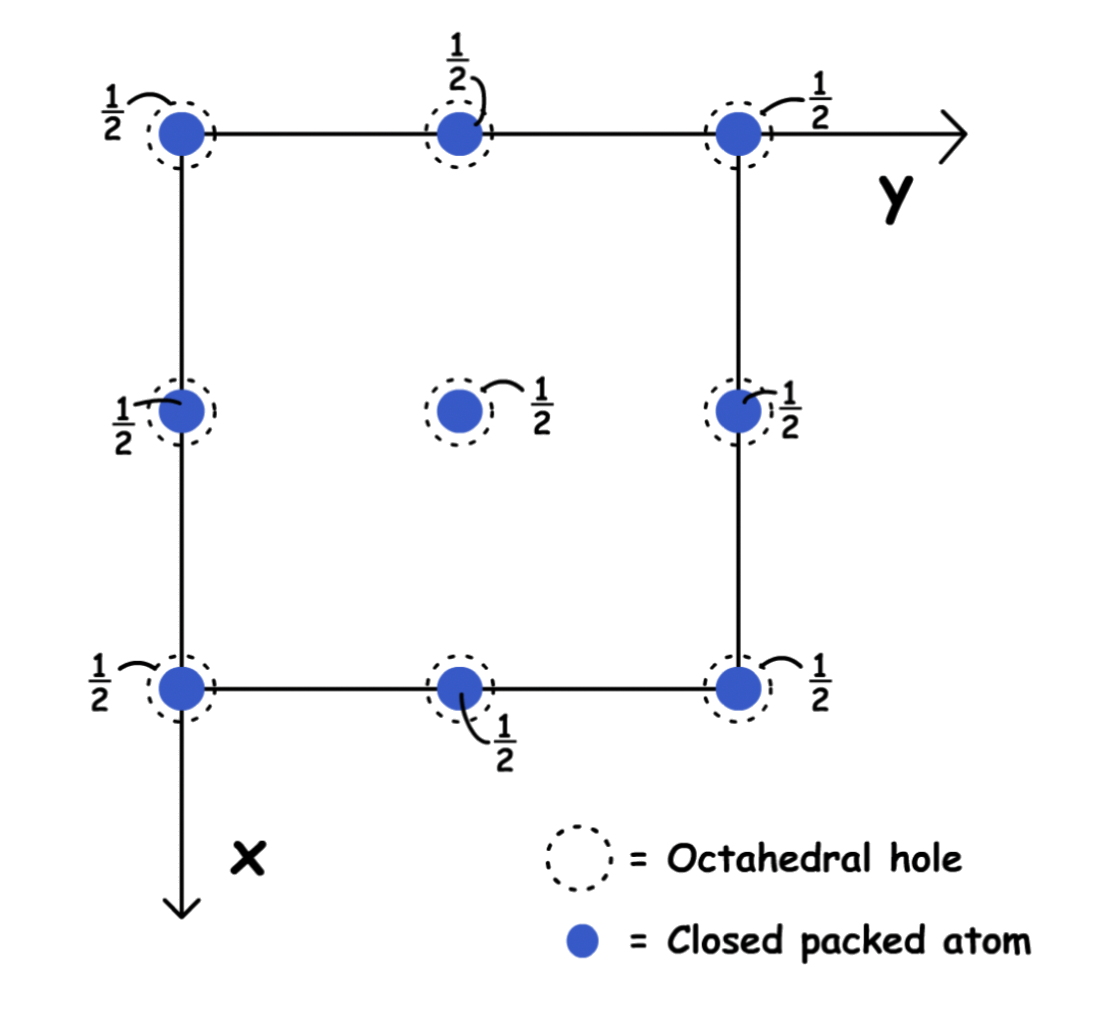
- In unit cell projection:
¶
Holes in Hexagonal Close-Pack
There are two tetrahedral holes around every corner of the unit cell
- In unit cell projection:
The atoms in the faces create a octahedral hole
- In unit cell projection: