¶ Harmonic Oscillator
The harmonic oscillator is not an accurate depiction of the vibrations of molecules as it uses the classical viewpoint
- The predictions made by the harmonic oscillator is only accurate for vibrations where the atoms are not moving away from each other at a great distance
¶ Selection Rules for Harmonic Oscillator
1. There must be a change in dipole moment upon vibration
The dipole moment operator in the transition dipole moment integral of vibrational spectroscopy is the change of dipole moment
The molecule does not need to have a permanent dipole to be IR-active
Homodiatomic molecules are IR-inactive2. Only transitions between adjacent energy level is possible
The quantum number n can only change by 1 each time
This selection rule is only applicable to harmonic oscillator, but not anharmonic oscillator
This selection rule is not applicable in real life¶ Solution to the Harmonic Oscillator
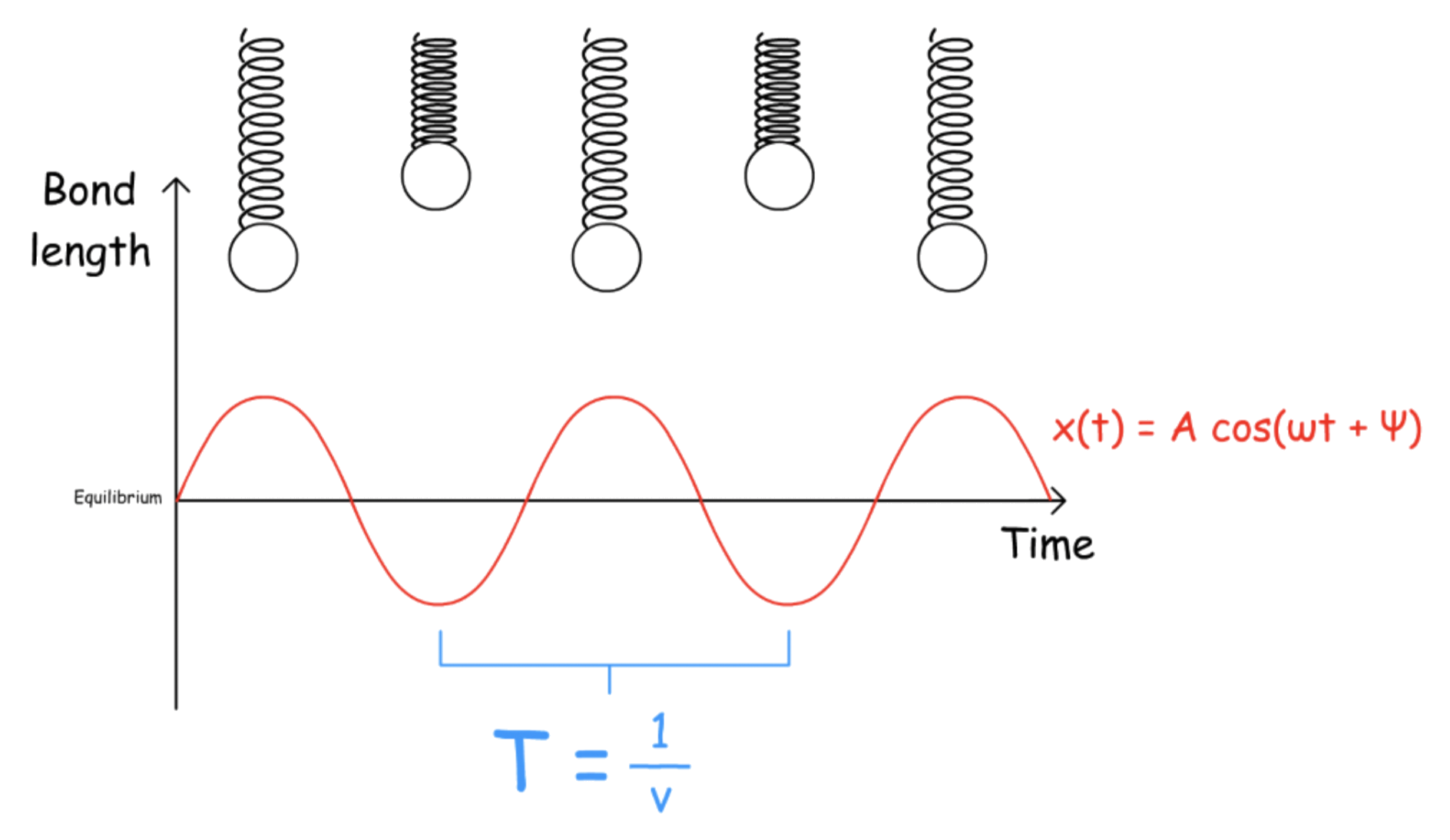
The harmonic oscillator treats a bond as a spring
- This allows us to relates the strength of the bond with a spring constant, k, hence the vibration of molecules can be described by Hooke's Law:
- We can then construct a differential equation using this force:
- Solving the equation gives us
When there is no energy lost, the motion of a harmonic oscillator will be periodic
- Every time a restoring force is exerted to stretch or compress the bond so that the atoms can return to their equilibrium positions, it will overcorrect itself, leading to the formation of a new restoring force of the opposite direction
There are a few parameters that define the motion
- is the angular frequency
- is the period of oscillation
- The natural frequency of oscillation ( ) is the reciprocal of the period
¶ Energy of Harmonic Oscillator
The energy level of harmonic oscillator is given by
- The vibrational wavefunction only contains one quantum number, , which is a non-negative real integer ( 0, 1, 2, 3, 4, 5... )
- There are no degenerate states
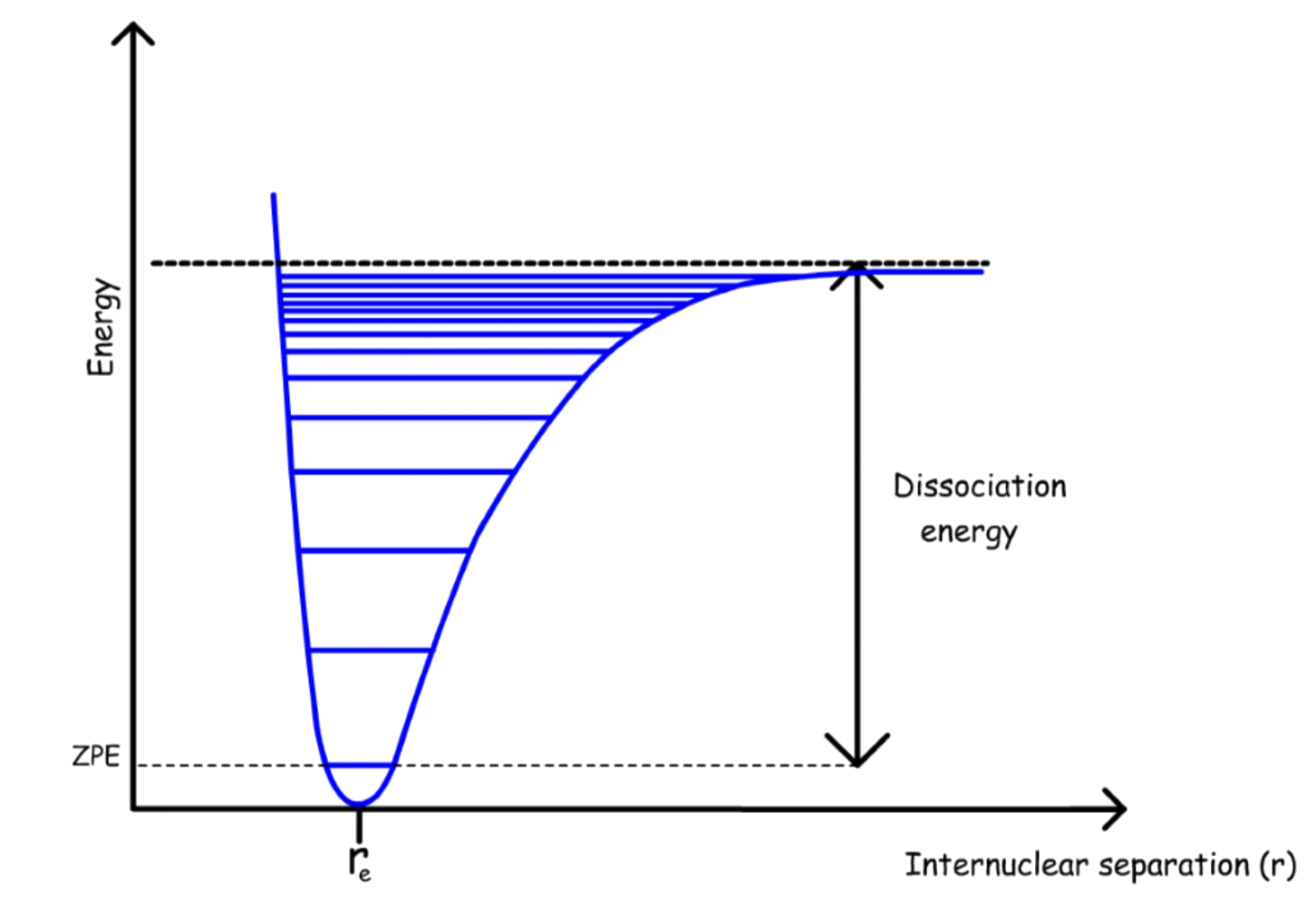
The lowest energy vibrational state occurs when
- The corresponding energy value called the zero point energy, and is a non-zero energy level
Since the slection rule only allows for transition across adjacent energy levels, the difference in energy level is given by
- The consequence of the selection rule is that the absorption energy is not dependent on the value of
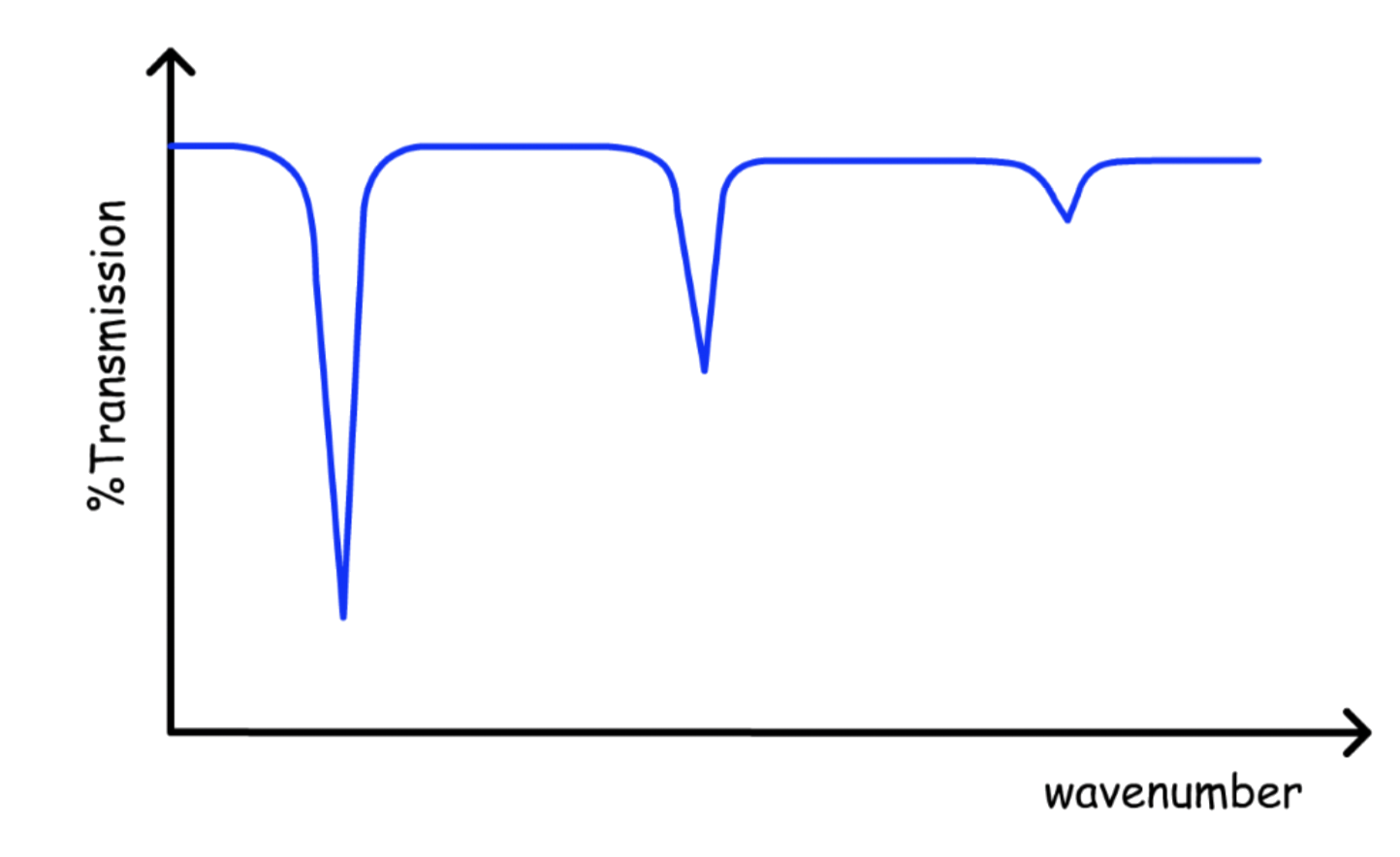
All energy levels are evenly spaced
- The absorption energy are the same for every transitions
- There is only one peak in the spectrum
¶ Anharmonic Oscillator
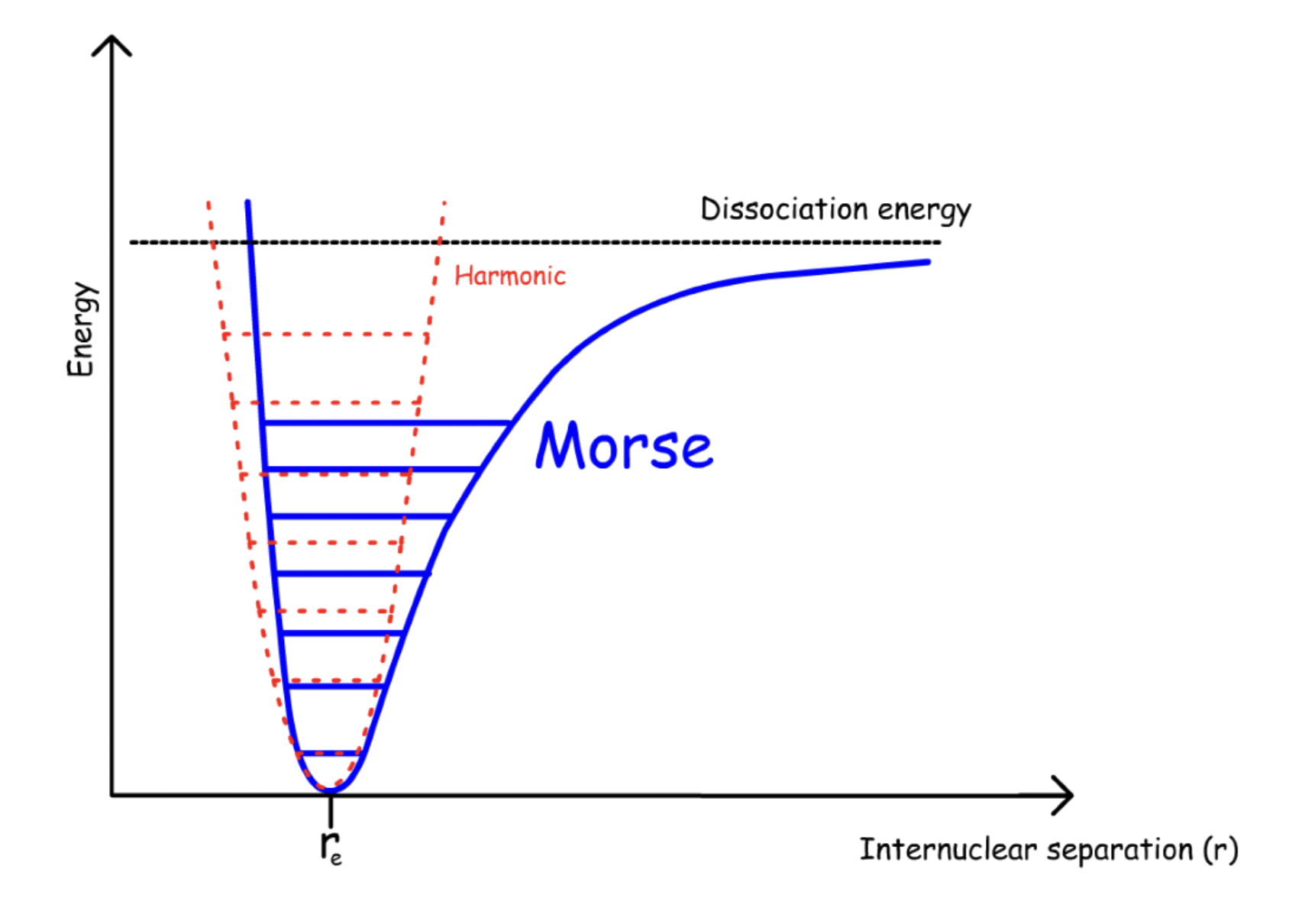
The anharmonic oscillator is a much more accurate model than the harmonic oscillator
One of the greatest failure of the harmonic oscillator model is that it does not take into account the fact that the repulsion force and attraction force are of different nature
- As a result, the actual potential energy will deviate from the harmonic model when the atoms are far apart from the equilibrium position
The nature of the repulsion and attraction force is fundamentally different
- When the two nucleus are getting closer, the repulsion force will skyrocket
- When the two atoms are far apart, the bond will dissociate, causing the attractive force to approach zero at infinity
The refined model which accounts for both phenomenon yields the Morse Potential
¶ Selection Rule for Anharmonic Oscillator
1. There must be a change in dipole moment upon vibration
The dipole moment operator in the transition dipole moment integral of vibrational spectroscopy is the change of dipole moment
The molecule does not need to have a permanent dipole to be IR-active
Homodiatomic molecules are IR-inactive2. Unlike the harmonic oscillator, there are no limitation on transitions
¶ Energy of Anharmonic Oscillator
The energy level of anharmonic oscillator is given by
- is the anharmonicity constant
- Increasing anharmonic effect at higher vibrational levels
- There are no degenerate states
The energy levels are not evenly spaced
- Converges as n increases
- Becomes basically continuous when n is large enough
- There are multiple peaks in the spectrum
The dissociation energy can be found from through the Morse Potential
- The sum of all the energies ( The sum of all hot bands ) will give the dissociation energy
- Note that the dissociation energy is measured from the lowest state ( n = 0 ), not the bottom of the potential well
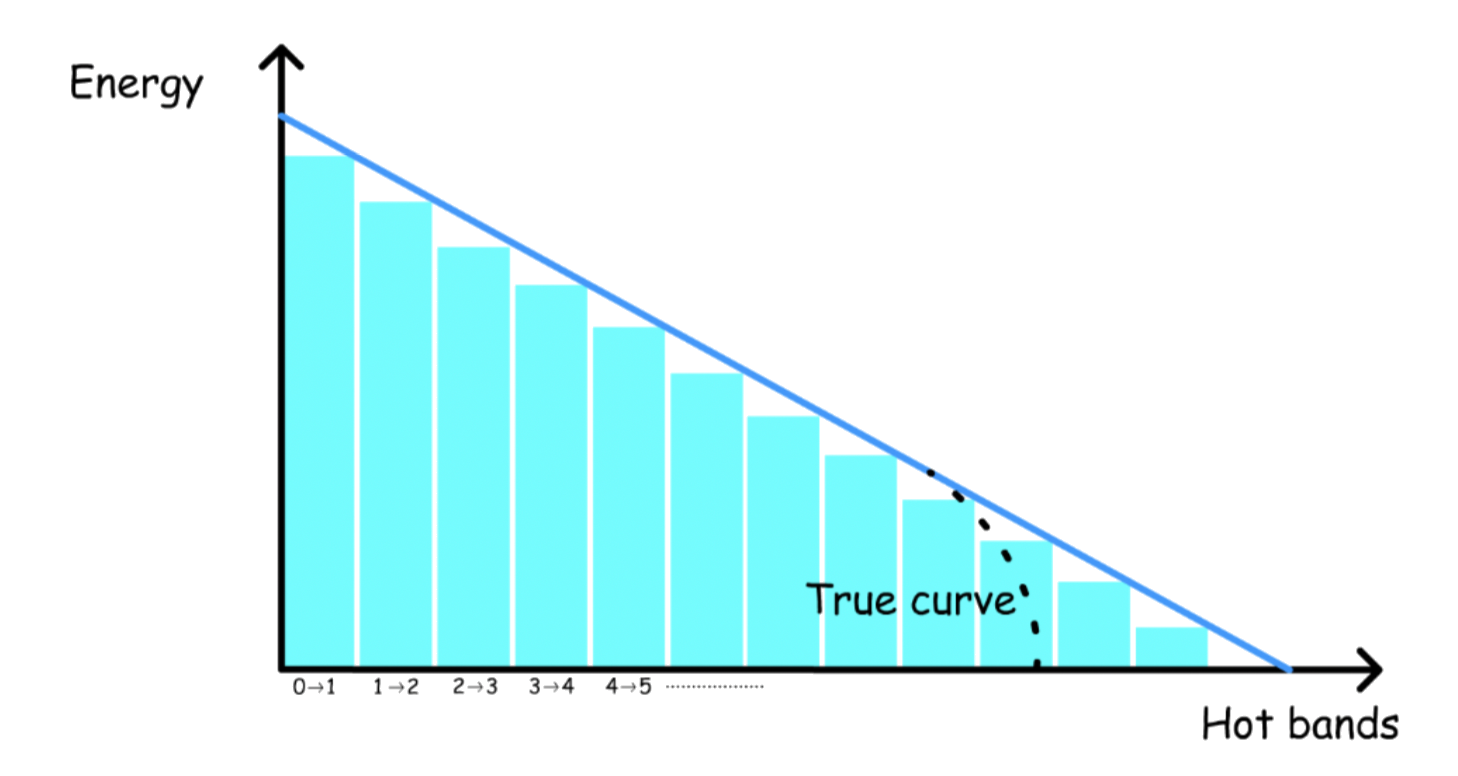
The dissociation energy can be found by calculating the area of the triangle: \frac{1}{2}\times\text{Transition energy of the fundamental\times \text{number of hot bands}}
- The triangular shape is an approximation, it will overestimate the dissociation energy
- Only lowest transitions are easy to measure, so a linear extrapolation is the only option
Unlike the harmonic oscillator, there is a finite number of energy levels ( quantum number ), which can be found from the dissociation energy graph
¶ Spectrum
Overtones
Since transitions other than the adjacent levels are allowed, there are series of transitions for every vibrational state
- Overtone results from transitions where is greater than one
- At low energy, only a few overtone can be seen
For transitions where is larger than 1, the peak will be denoted as the overtone
The higher the order of overtone, the smaller the amplitude
- The transition dipole is lower for larger transitions
The intensity of the peak decrease from left to right
- Larger transition = larger energy
Hot Bands
In the anharmonic oscillator model, since the energy levels are not evenly spaced, different series will emerge
- These series will appear as hot bands in the spectrum
- At low energy, only a few hot bands can be seen
For the transition series starting from , the series of hot band is called the fundamentals
- For the other transition series, the series of hot bands are called the hot band
The higher the order of hot band, the lower the amplitude
- The population of higher energy level is lower than that of lower energy ( Boltzmann Distribution )
The intensity of the peak decrease from the right to left
- Hot bands of higher order red shifts
- The energy level of vibrational states converges, so the absorption energy of lower order hot bands are higher
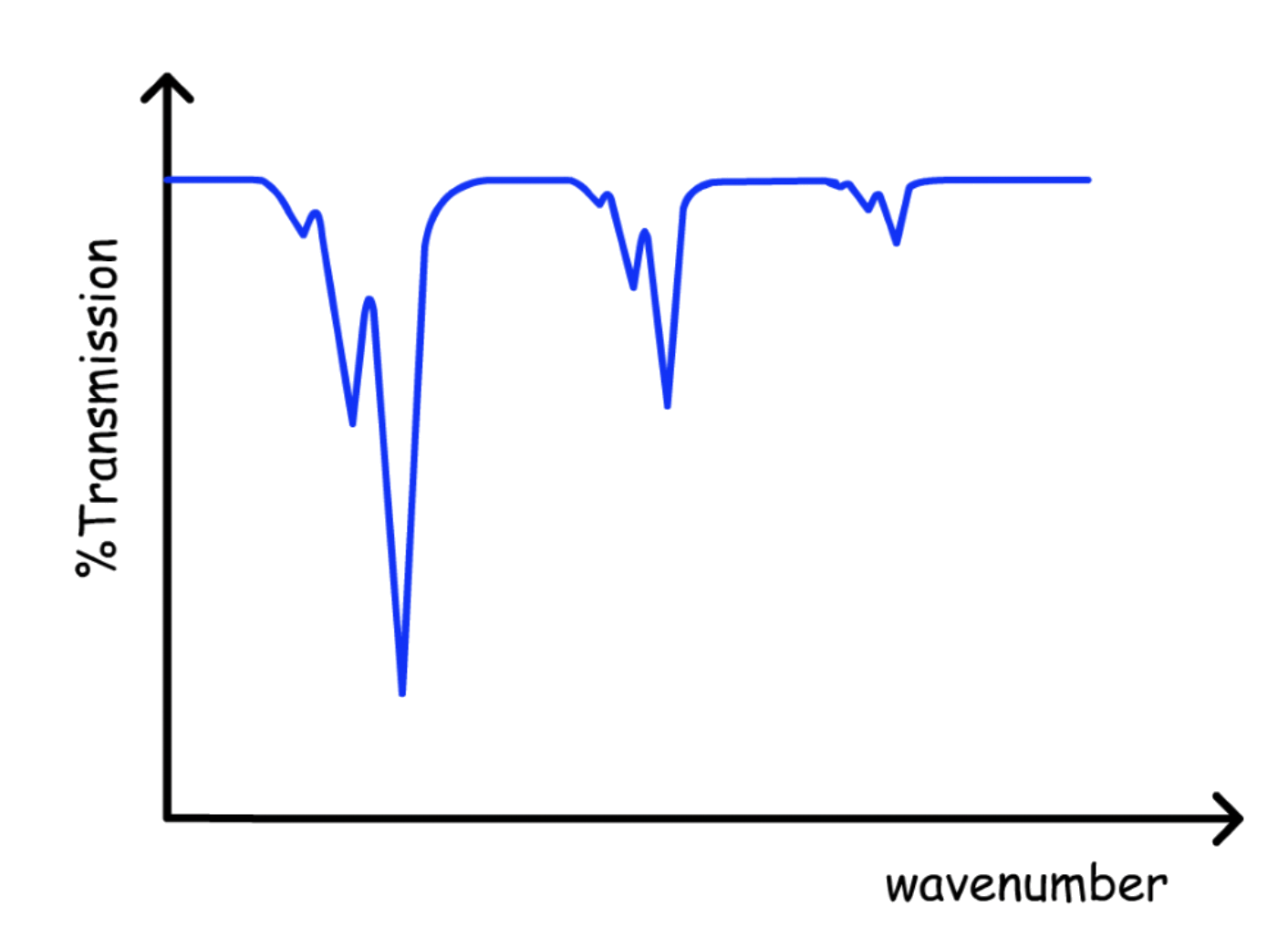
Combining Hot Bands and Overtones will give us the spectrum
The higher the order the overtone or the hot band is, the lower the intensity
- The reason for a decreasing intensity is different for each of them
- The intensity of overtones decreases because the transition energy, increases, which decreases the transition dipole
- The intensity of hot bands decreases because higher vibration states are less populated
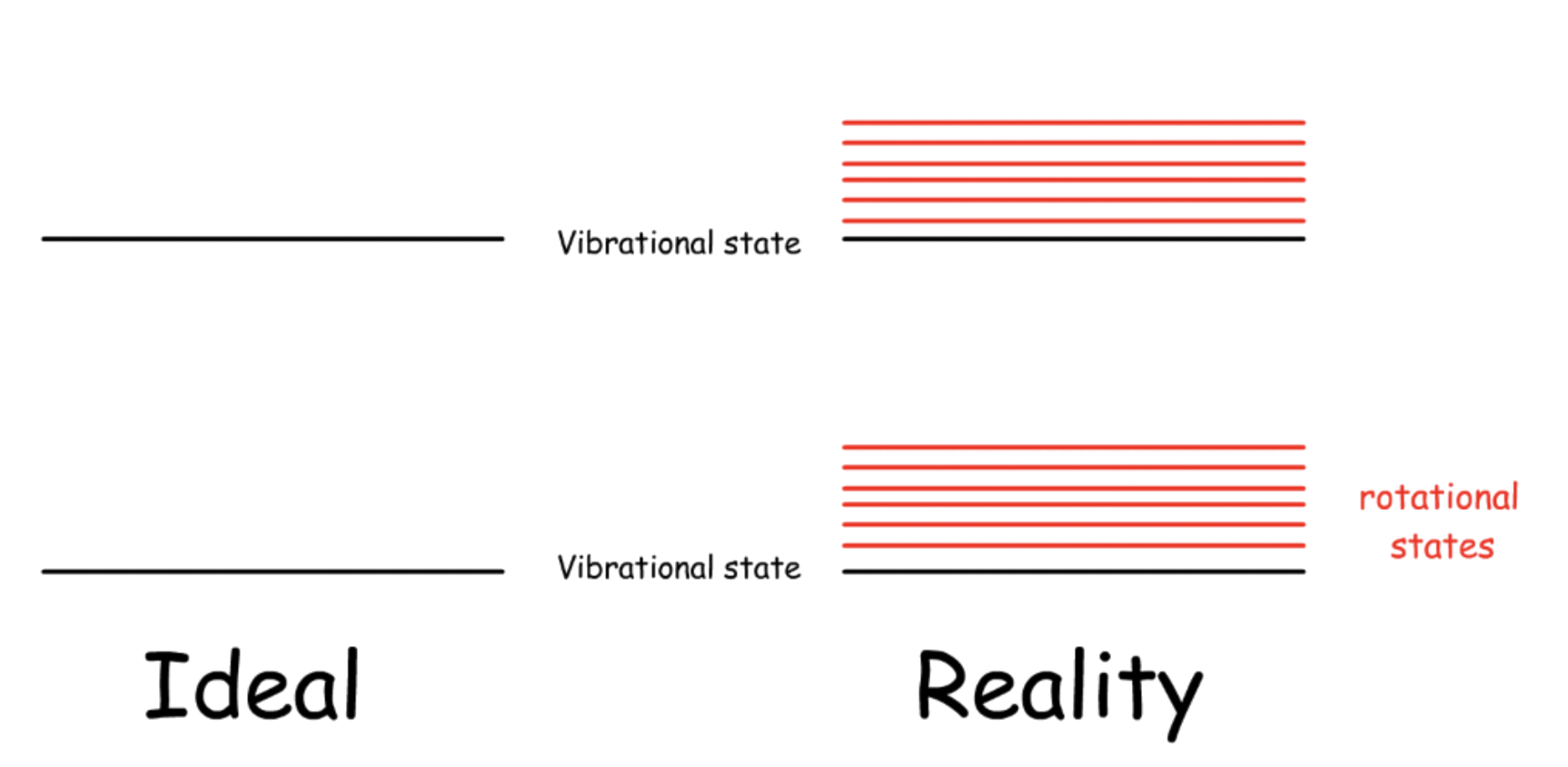
¶ Rotational-Vibrational Spectroscopy
For every vibrational state, it forms a subset of rotational levels
Rotational states are stacked on vibrational states
- As a result, transitions in vibrational spectroscopy will be complicated
The rotational constant, , is different for each set of rotational states
- The bond length changes during vibration
Now that we are considering both transitions together, we also have to consider the selection rules for each spectroscopy:
- Rotational spectroscopy:
- Vibrational spectroscopy: no restriction on
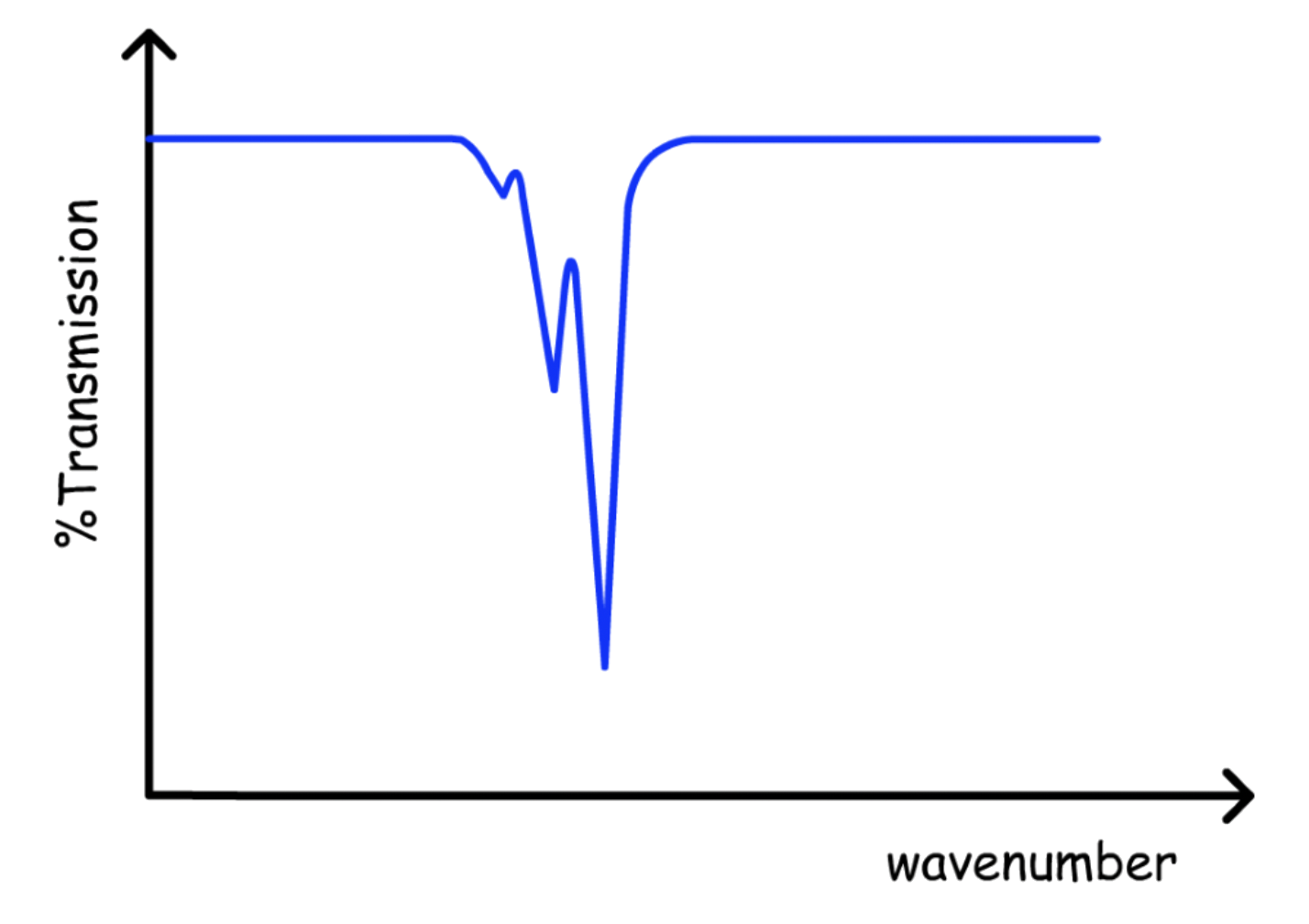
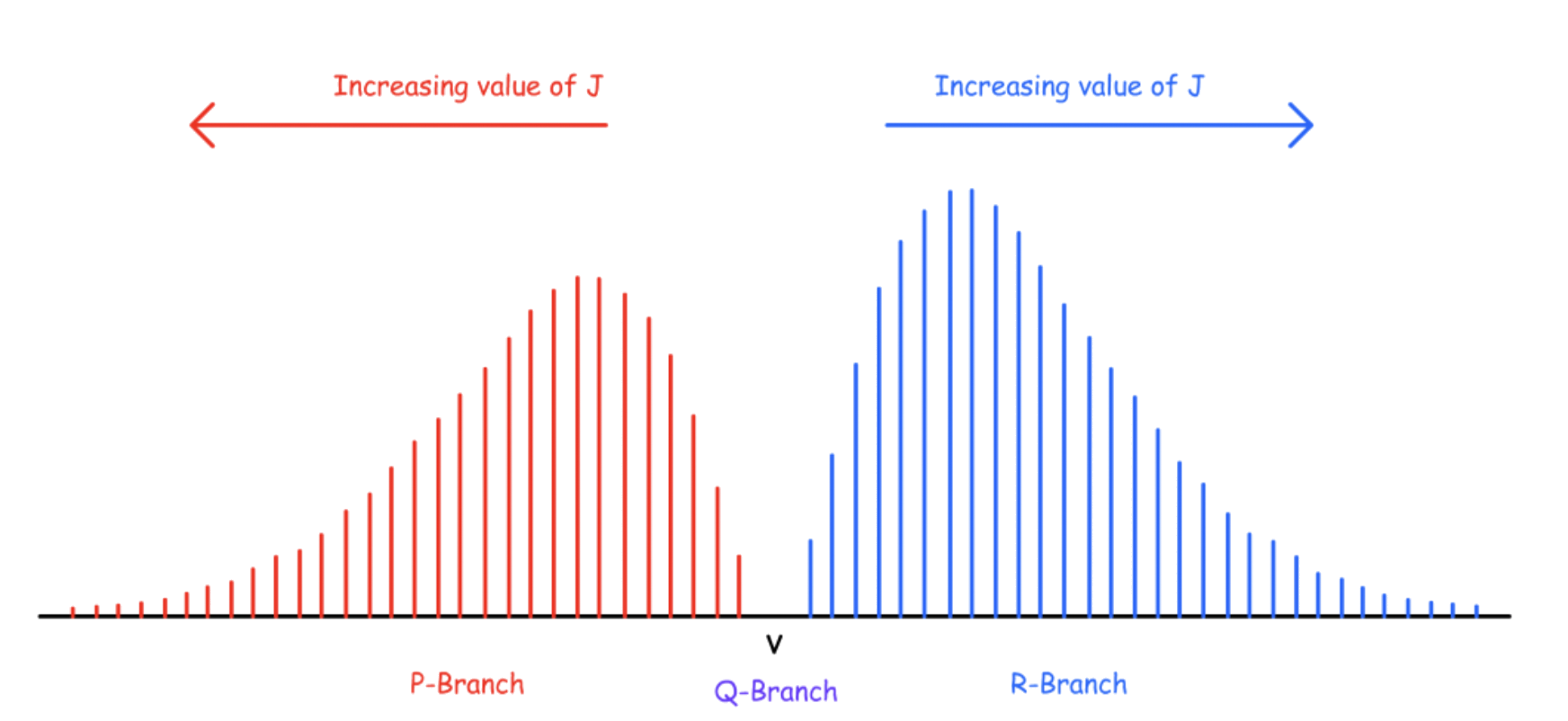
When is set to constant, there will be three series of transitions:
- Q-Branch, P-Branch, R-Branch
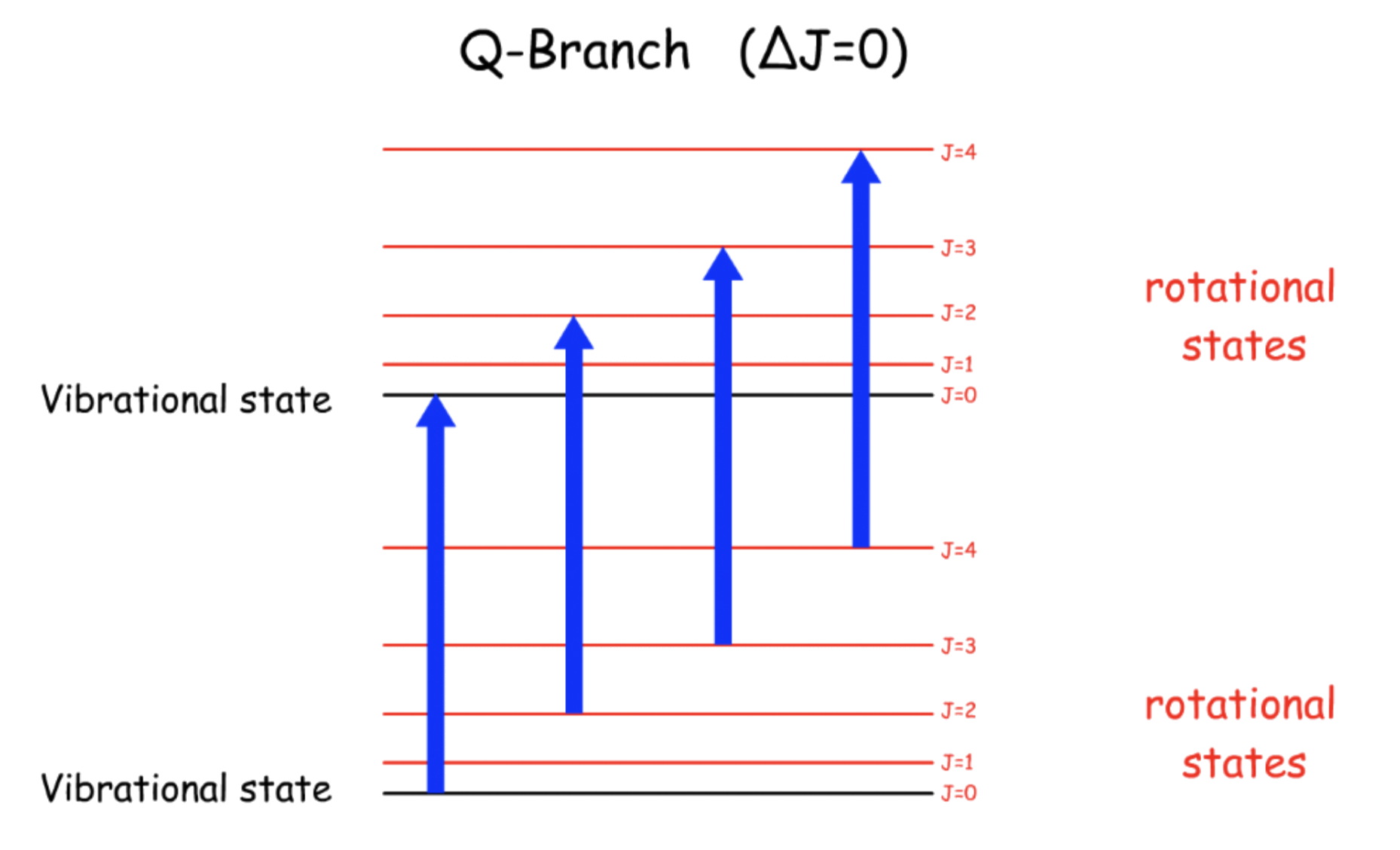
¶ Q-Branch
Transition Energy, ΔE = hv \ - \ \text
Since it does not obey the selection rules of the rotational spectroscopy, the transitions of Q-branch is forbidden
- The fundamental transition will not appear in the spectrum
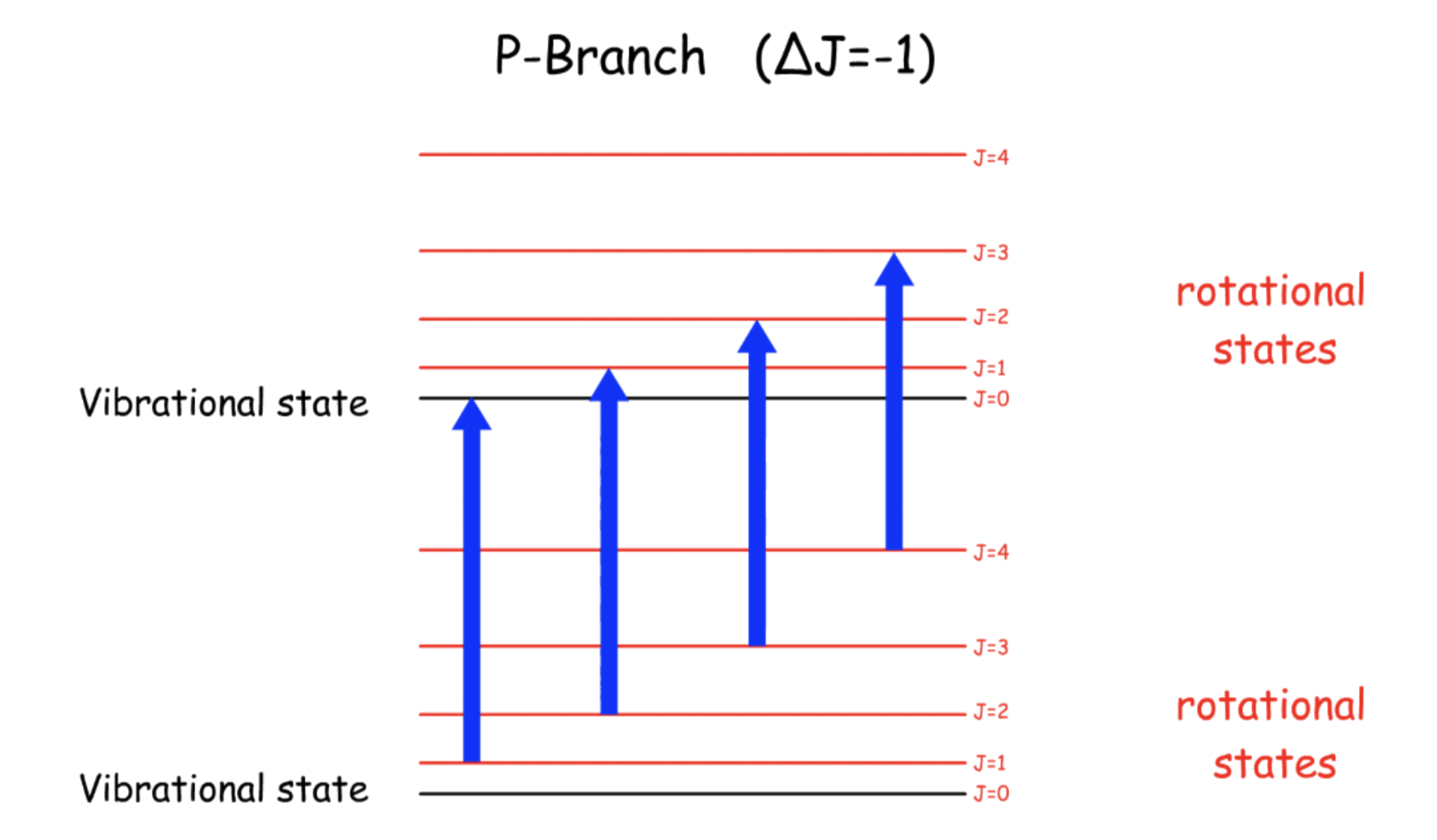
¶ P-Branch
Transition Energy, ΔE = hv – 2B ( J + 1 ) - \text
- Since the term representing the rotational energy has a negative sign, the transition energy decreases for greater value of J
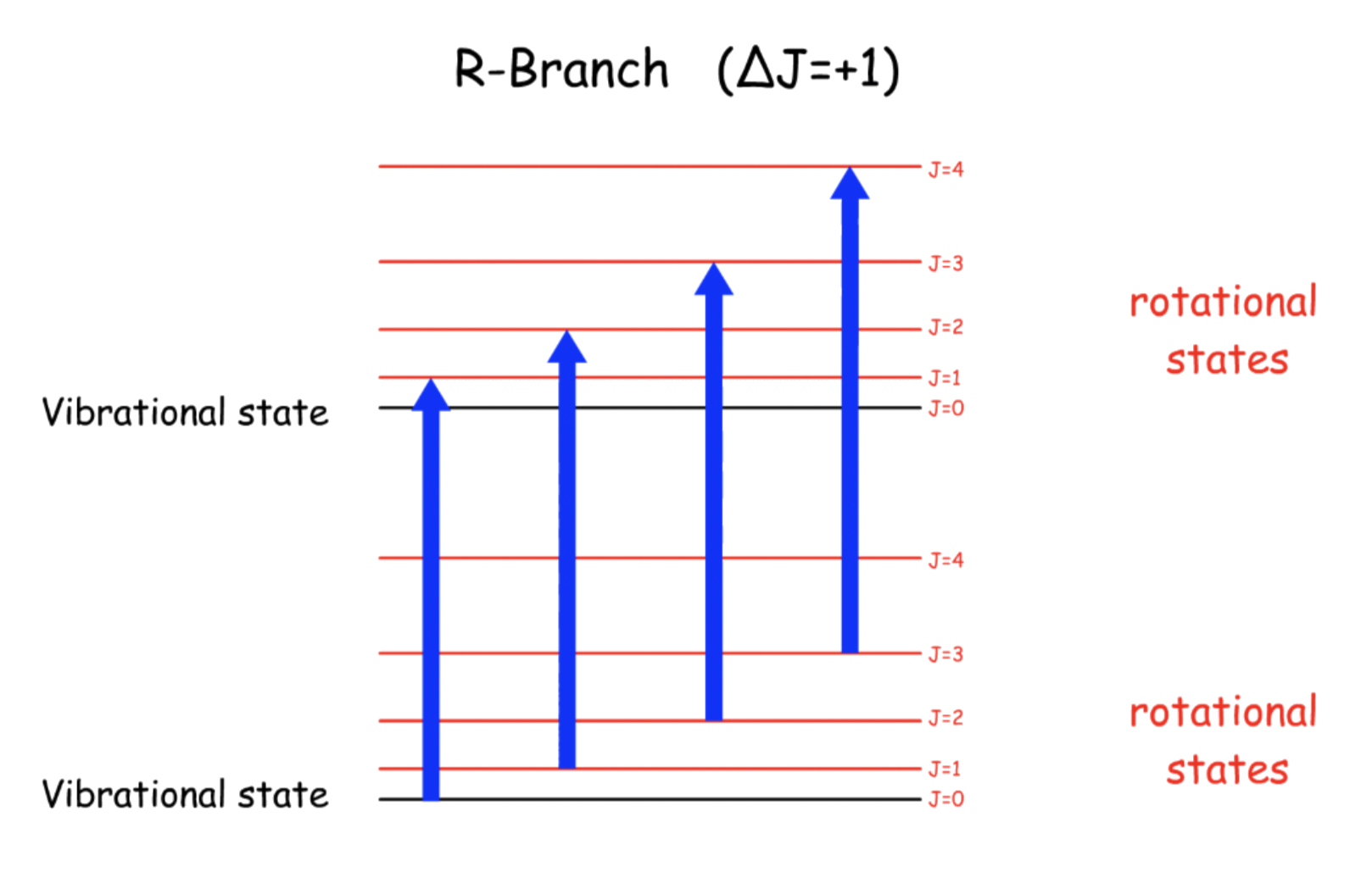
¶ R-Branch
Transition Energy, ΔE = hv + 2B ( J + 1 ) - \text
- Since the term representing the rotational energy has a negative sign, the transition energy increases for greater value of J
¶ Overall Effect
The overall effect is what we will see if we zoom in on one peak
The shape of the two branches can be explained by the Boltzmann Distribution
- Due to the degeneracy of rotational states, the maximum population, hence intensity, is not when
The P-branch will be complicated by isotopic effects
The distances between peaks are roughly
- The width of the Q-Branch is roughly
- The equilibrium frequency is away from both the lowest P-Branch and Q-Branch transitions
¶ Degree of Freedom
The degrees of freedom (DOF) of a mechanical system is the number of independent parameters that define its configuration or state
- The number of independent ways in which a molecule or atom can exhibit motion
Degree of Freedom in terms of coordinates can be defined as the number of coordinates needed to specify all the atoms in a molecule
- Each atom is described by 3 coordinates ( x, y, z )
The degree of freedom of a molecule = 3N, where N is the number of atoms present in the moleculeTypes of motion: Translation, rotation and vibration ( stretching and bending )
- There are always 3 degree of freedom in translation for a 3D object ( when all the atoms are moving in the same direction )
- There are normally 3 degree of freedom in rotation, however for linear molecules, there are only two
- Linear molecules cannot rotate along the internuclear axis since the moment of inertia is 0
- Non-linear molecules are free to rotate along the x, y and z-axes
The degree of freedom of vibration is the degree of freedom left after accounting for translation and rotation:
- For linear molecules, the number of vibration modes (stretching + bending) is 3N – 5
- For non-linear molecules, the number of vibration modes (stretching + bending) is 3N – 6
¶ Vibrational Modes
There are three vibrational modes:
- Symmetric stretching, asymmetric stretching and bending
- Vibrational modes of the same type can be degenerate of each other
Stretching is a change in bond length
- The number of stretching modes is equal to the number of bonds on the molecule
-Double or triple bonds are counted as one in this context- A symmetric stretch occurs when atoms move in opposite directions as the bonds shrink or stretch
- An asymmetric stretch occurs when some atoms move in the same direction while others move in the opposite direction
- It takes more energy to perform an asymmetric stretch than a symmetric one
Bending is a change in bond angle
- The number of stretching modes is equal to the total number of vibrational modes minus the number of modes of stretching
- When the molecule is bending in and out of paper, ⊕ and ⊖ can be used to represent the relative position of atoms/ groups
- ⊕ means that the atom/ group is out of paper and ⊖ means that the atom/ group is inside the paper