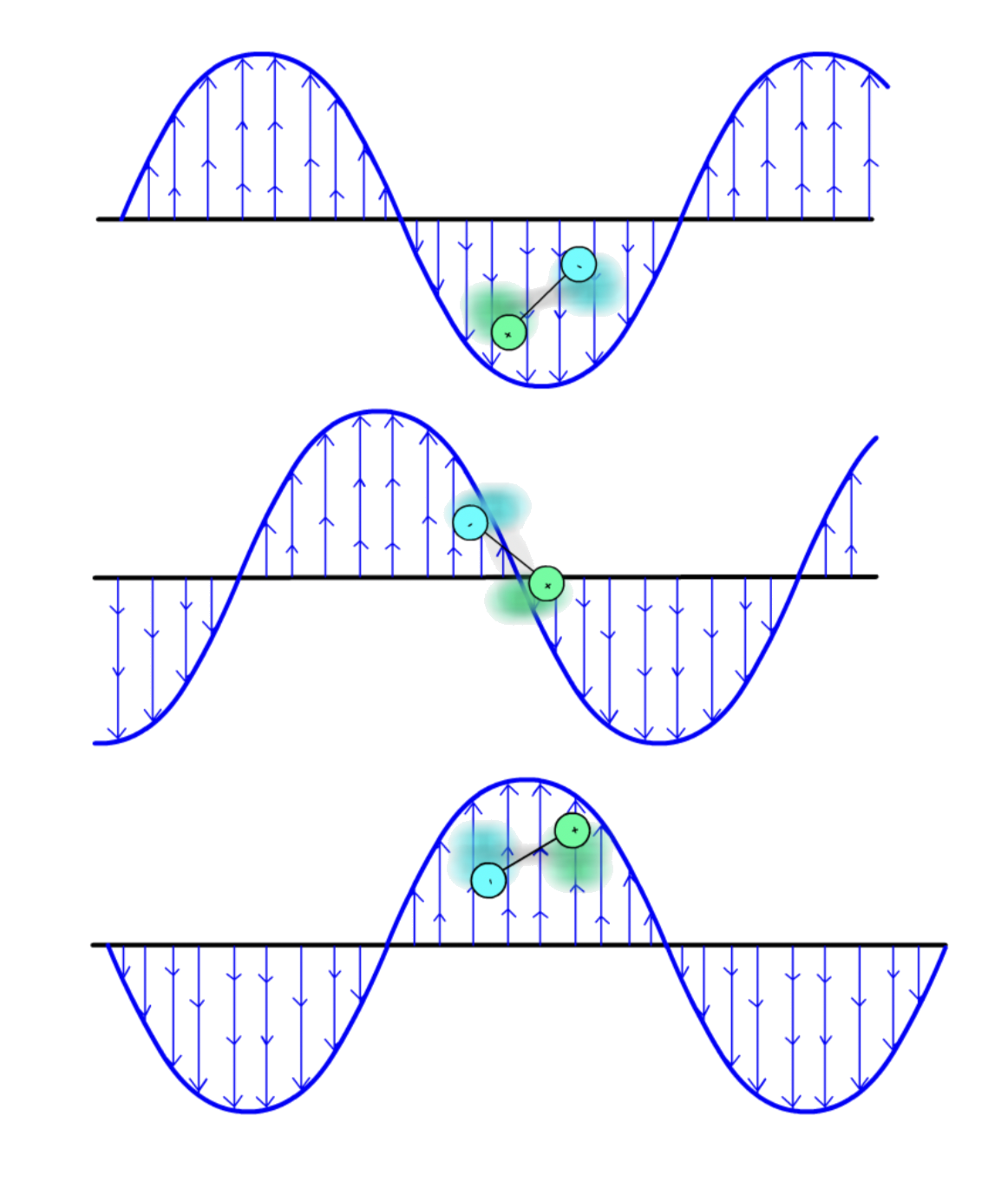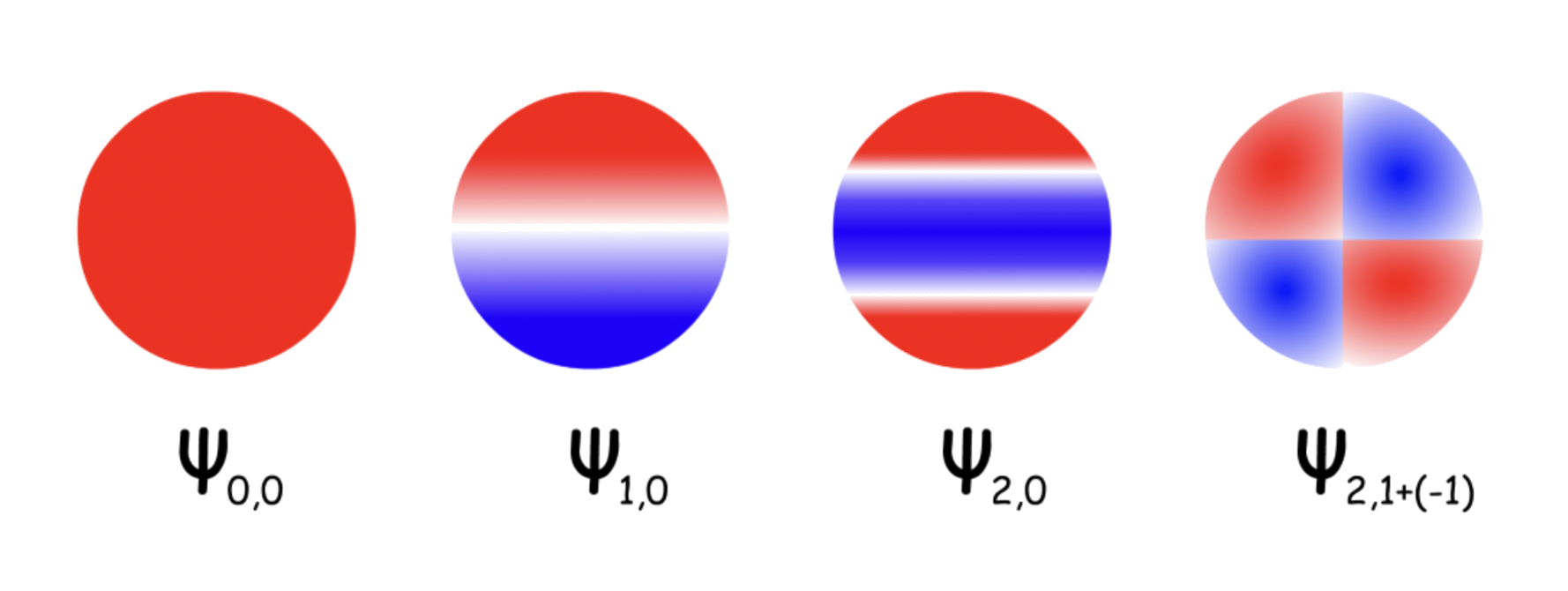¶ Fundamentals
¶ Selection Rules
In order for transitions to happen, the transition dipole must not be zero, which only happens if two rules are obeyed
1. Only molecules with a permanent dipole is considered as microwave active
- When dipole molecule rotates, they will generate an oscillating electric field, which can be detected (Classical viewpoint)
- When dipole molecule is in an oscillating field ( microwave ) , it will try to align itself with the field continuously, which results in rotation. The work done on the molecule is tantamount to the absorption of microwave
- As the electric field changes, the direction of the field line reverses. The molecule begins to accelerate so as to “match” the changing electric field and undergoes rotational motion
- When the frequency of light matches the frequency of molecular oscillation, light will transfer energy to the molecule
In rotational spectroscopy, the dipole moment operator refers to the permanent dipole of the molecule
- If there is no permanent dipole (i.e. dipole moment=0), the transition dipole moment integral will be 0
2. The transition in energy level can only be
Functions with even J values are symmetric with respect to the origin of the reference frame, while functions with an odd J value are anti-symmetric
The wavefunction of the initial and final state must be different (one even and one odd) such that the overall integral will be an even function when they are multiplied with the dipole moment (odd function)Transitions involving or any positive or negative even number are not allowed
- They involve wavefunctions with the same symmetry, which produces an even function
- For equals to odd number larger than 1, the integral of the overall even function is still zero
- Hence, only transitions between adjacent levels are permitted
¶ Types of Rotation
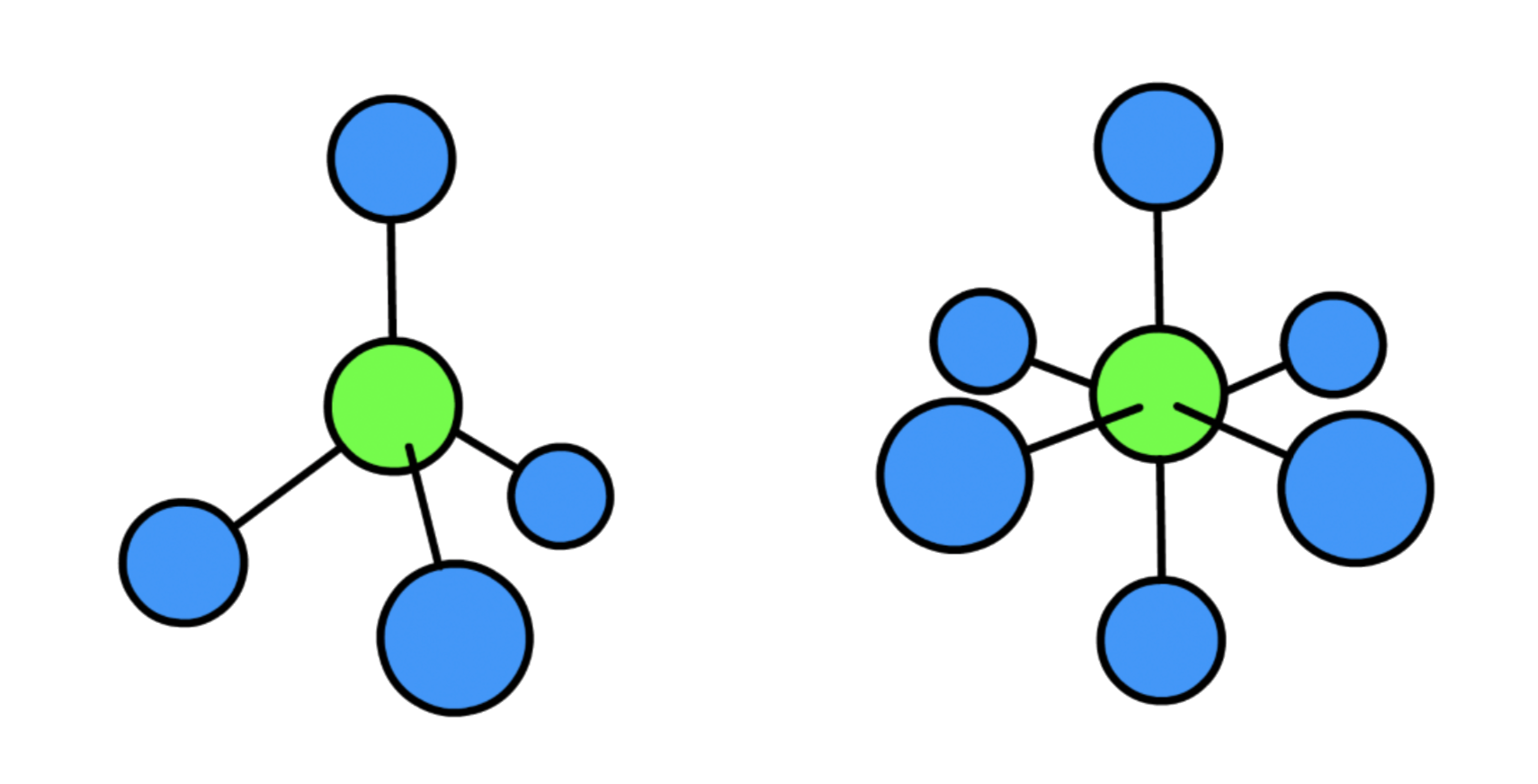
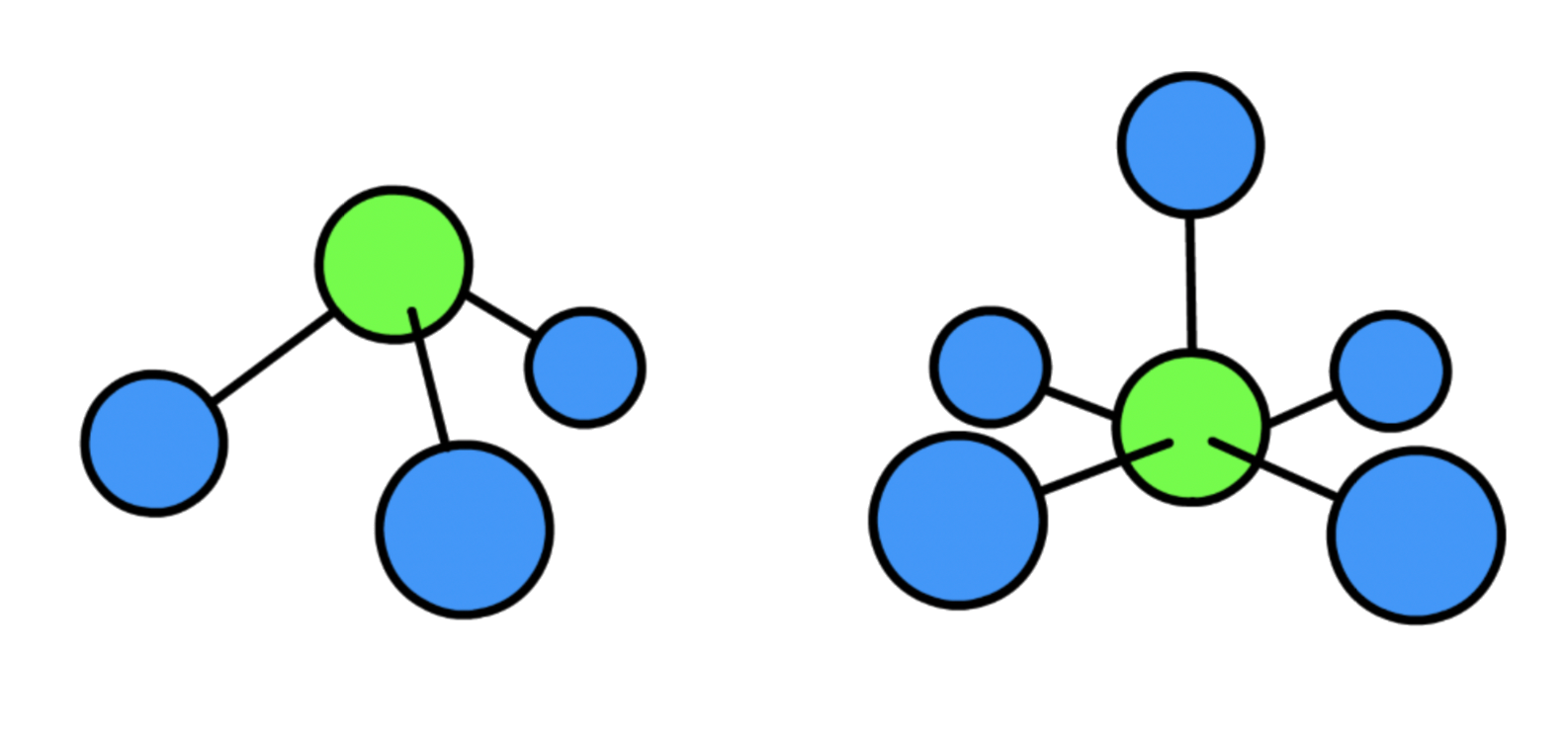
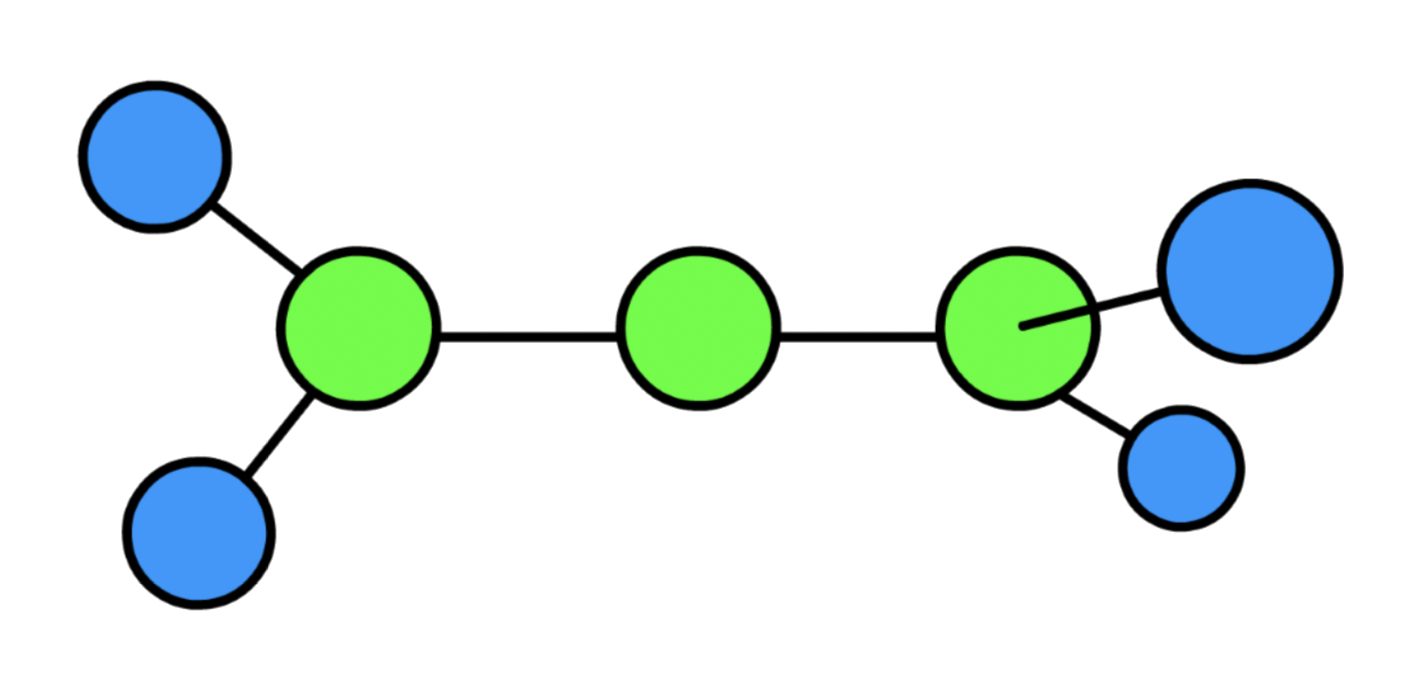
We can catagorize molecules into 4 main types based on wheter their moment of inertia ( ) along different dimension is the same
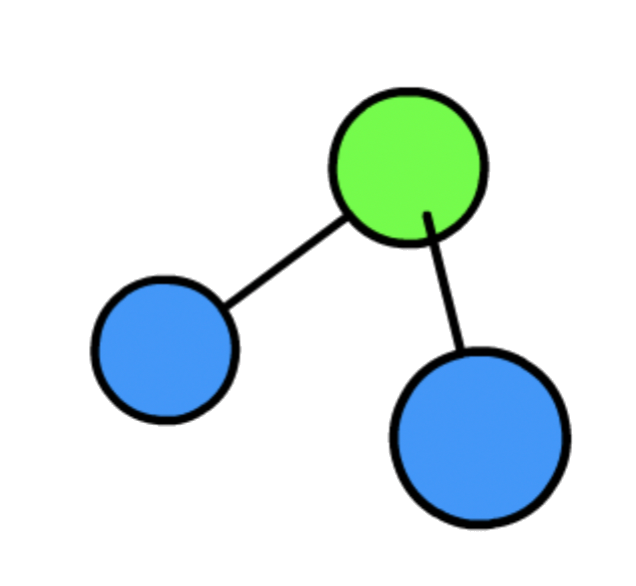
1. Linear Rotor
- ;
- Since two of the three moment of inertia is identical and the remaining one has a value of zero, there is only one moment of inertia for linear rotation
- The moment of inertia along the internuclear axis is zero because
2. Spherical Rotor
- Due to the symmetry of the molecule, spherical rotor only has one moment of inertia
- Since permanent dipole is required, if the spherical rotor is completely rigid, it will not have a pure rotational spectrum
- Vibration or non-rigid centrifugal force can distort the geometry of the molecule, rendering it microwave active
3. Symmetric Rotor
- Symmetric rotor have two different moment of inertia
They are two types of symmetric rotor: Oblate or Prolate
- Oblate symmetric rotor ( )
- Oblate symmetric rotor ( )
4. Asymmetric Rotor
- There are three distinct moment of inertia for asymmetric rotors
¶ Rigid Diatomic Molecules
To study rotational spectroscopy, let us turn to the simplest type of rotor, rigid diatomic molecules
- Understanding properties of this simple case will allow us to make some important generalization
¶ Moment of Inertia
It is hard to find the center of mass, so the reduced mass ( ) is introduced to make finding the moment of inertia easier
- Since the center of mass is determined by the ratio of masses, the reduced mass is a term which factors in the location of the center of mass without calculating it
The r now stands for bond length instead of the distance of mass from center of mass
¶ Rotational Spectrum
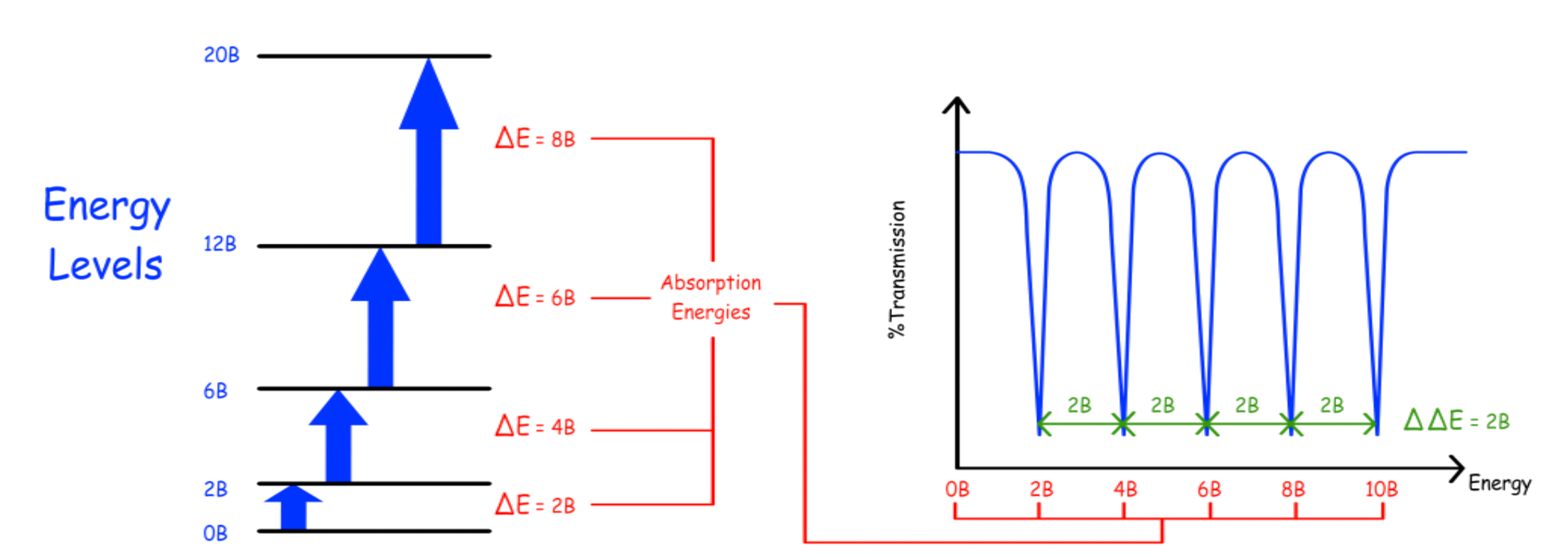
The rotational energy is directly proportional to the rotational quantum number ( )
- is the rotational constant
depends on the moment of inertia and thus differ with size and mass ( different for different molecules )
The energy for transitioning from one rotational energy level to another is given by
- Since there is no zero point energy in rotational spectroscopy, the energy level of the ground state is zero
We can therefore derive the rotational spectrum for a rigid diatomic rotor
The difference in absorption energy (The difference in the difference in energy level, ) is always
- This is no longer true when we do not consider the rotor to be rigid
- There is no peak in 0B as a ΔJ = 0 transition is forbidden
¶ Population of Rotational Energy
We can determine the relative population of rotational energy using the Boltzmann Distribution
- The number of degenerate rotational energy levels for a particular J value is given by
- Due to the selection rule, we know that :
- Substituting in the expression of in terms of
To calculate what value of J corresponds to the maximum population, we need to find the ratio of population of the ground state ( ) and any other excited state:
- Since the energy of the ground state is zero, can be substituted to the energy of the excited level
- Since there is no degeneracy in the ground state, the degeneracy term can be substitiuted as the number of degeneracy level of the excited state
The maximum population will no longer be at the lowest energy level
- This is because the number of degeneracy increases with Jf and the exponential function decreases with
- can be found by performing the differentiation , which gives the solution of
- When using this equation, if the value of Jmax obtained is not an integer, DO NOT round-off the value. Instead, plug in the nearest two integers to the Boltzmann Distribution equation to find out which J value corresponds to a higher population
¶ Isotopic Effect
The isotope will have a different mass, which will change the value of the rotational constant
- Isotopes have a greater mass, which decreases the magnitude of the rotation constant ( red shifting )
A change in mass will result in a change in several values:
- The ratio of the change is the same for all of them:
To account for isotopic effects, we simply have to overlay the spectrum with its shifted counterpart
- This is assuming that the bond length remains unchanged
¶ Non-Rigid Diatomic molecules
When molecules are rotating, the atoms will experience a centrifugal force that pulls them outward, which results in a larger radius
- The force is proportional to the square of the angular velocity, so a faster rotation will result in a stronger centrifugal force
- The bond between the atoms is like a spring, which will exert another force to pull them back to their equilibrium position ( Hooke's Law )
¶ Energy of non-rigid diatomic molecules
To account for the change in bond length due to the distortion, we will introduce the centrifugal distortion constant, D:
- The centrifugal force constant is inversely proportional to the force constant, k
- In other words, the stronger the bond, the smaller the adjustment
The adjusted equation for the rotational energy level now becomes
- Hence, the difference in energy level
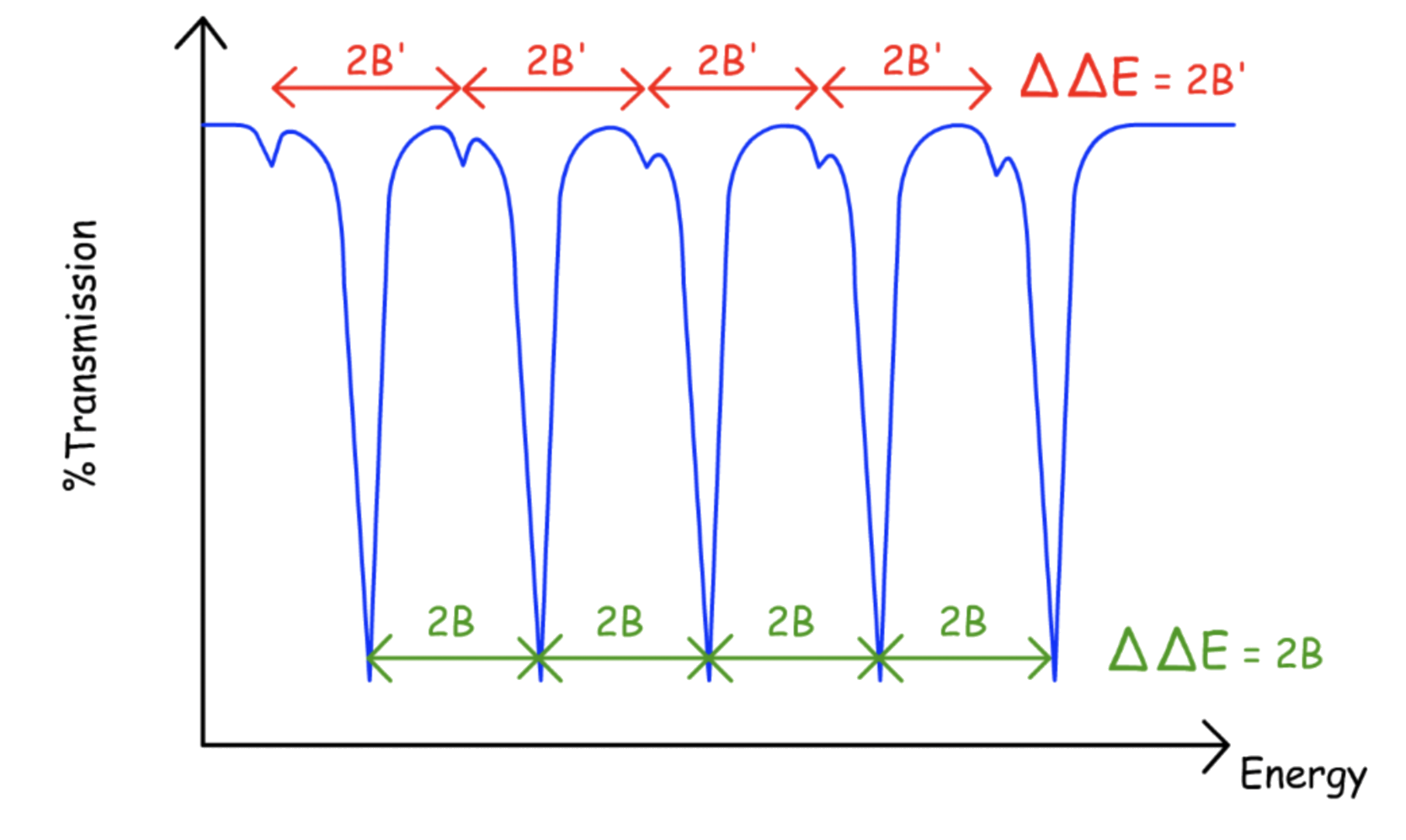
The effect of the correction becomes more significant as the value of J increases
- For small values of J, its energy levels can be approximated by the rigid rotor
- For large values of J, its energy level will deviate from that of the rigid rotor
The difference in absorption energy decreases as J increases
- The peak converges
- The distances between peaks can no longer be characterized by 2B
All the peaks are red shifted, peaks corresponding to a greater J values shifts to a greater degree