¶ Basic Principle of Crystal Field Theory
Crystal Field Theory describes bonding in transition metal complexes
- It describes the breaking of degeneracies of electron orbital states, usually d or f orbitals, due to a static electric field produced by ligands
- It successfully accounts for some magnetic properties, colors, hydration enthalpies, and spinel structures of transition metal complexes, but it does not attempt to describe bonding
Crystal Field Theory is a purely ionic description of bonding in transition metal complexes
- It is assumed that the ions are simple point charges
- All interactions between the ligands and the metal center are thought as electrostatic attraction and repulsion
¶ Crystal Field Splitting
The degeneracy of the d-orbitals is lifted due to the adoption of different geometry
- The d-orbitals of the metal center are split into different energy levels depending on the geometry of the complex
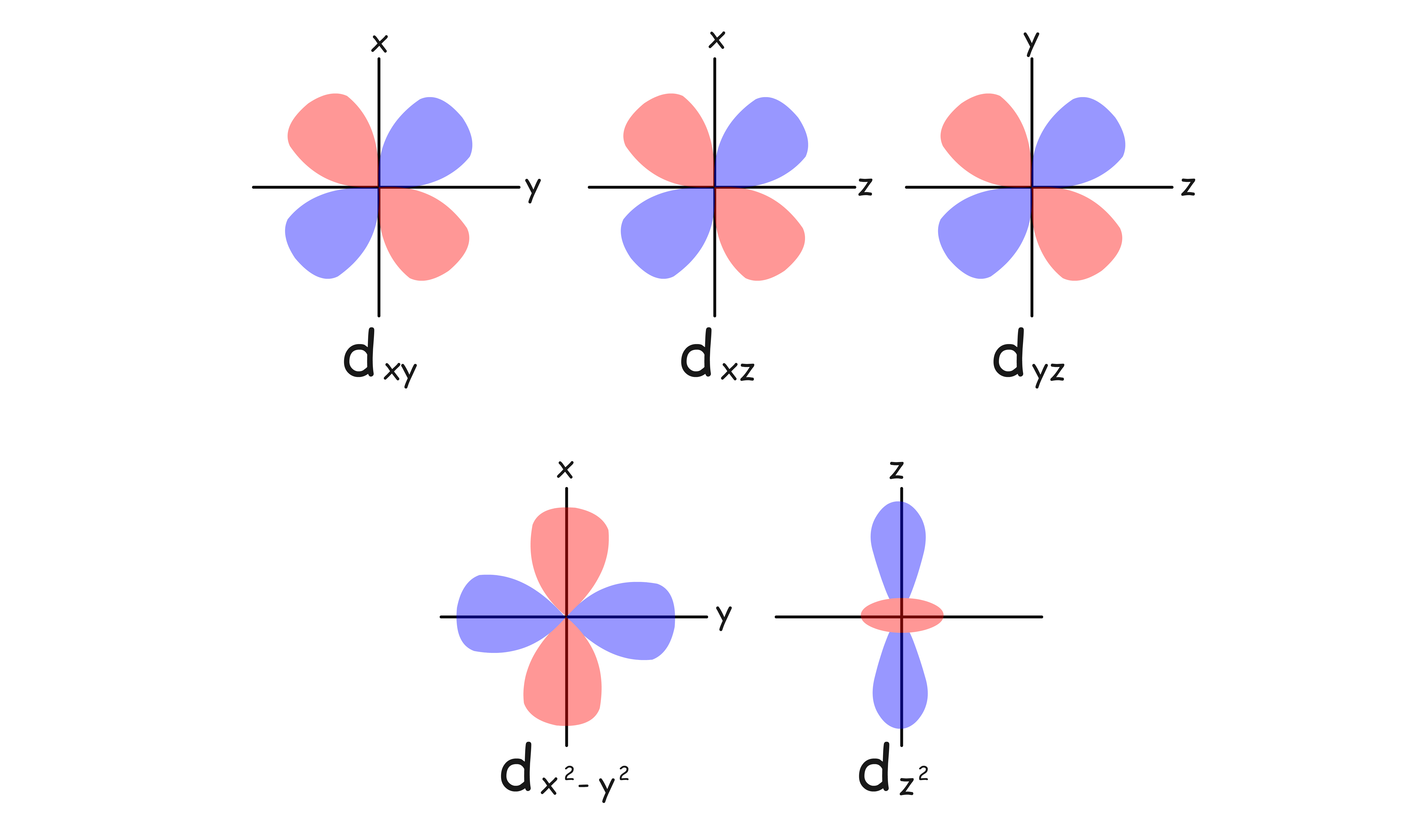
The reason why different geometry lead to different combinations of energy level is due to the peculiar shapes of d-orbitals
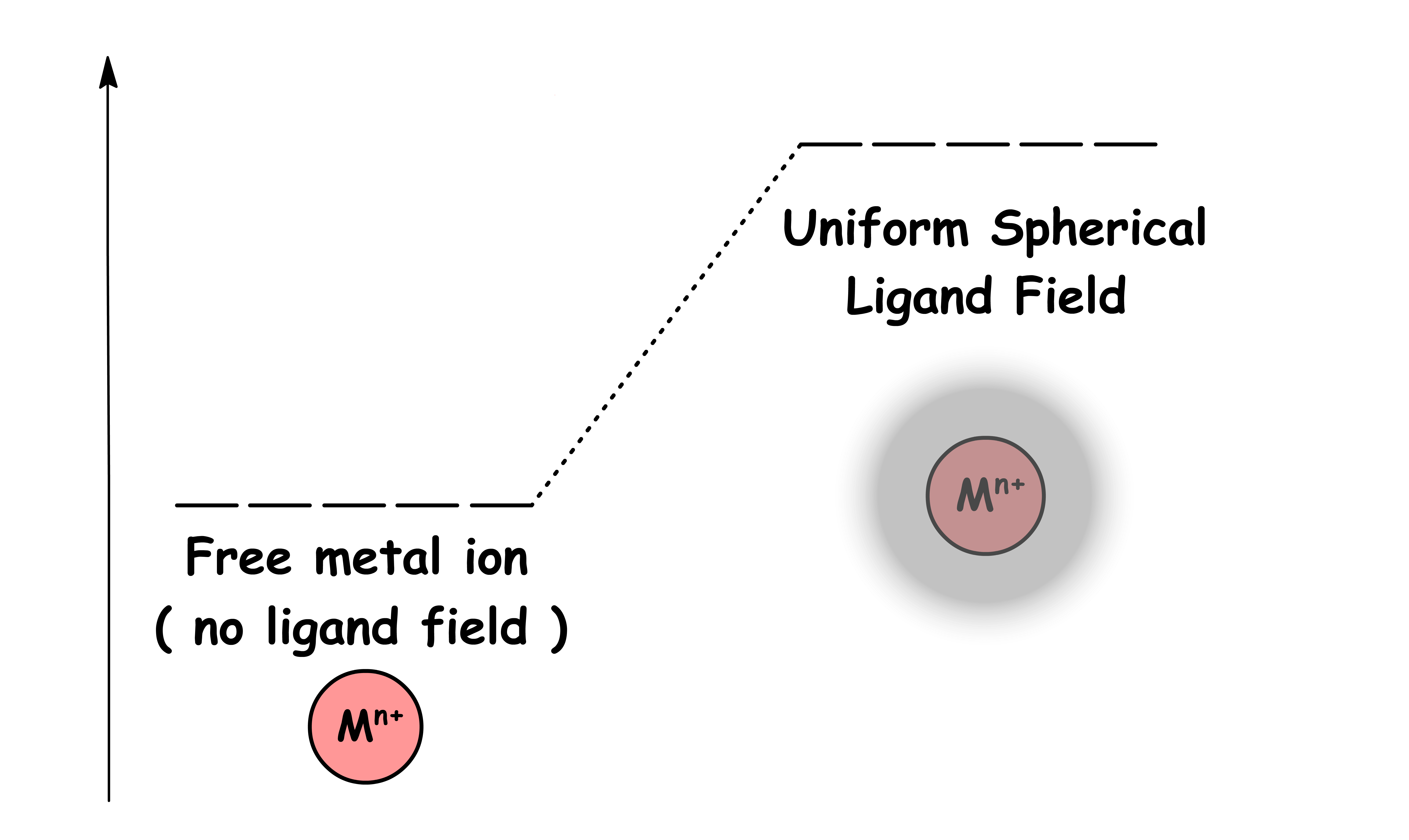
When the metal cation is in isolation, all five d-orbitals are degenerate
We can then consider the ligands bound to the metal center is a negatively charged uniform sphere
- We approximate the ligand sphere to be negatively charged because ligands must have lone pairs in order to bind to the metal
- There are electrostatic repulsion between the electrons in the d-orbitals and the ligand field sphere, hence the d-orbitals are destabilized
- Since the charged of the sphere is uniform, all the d-orbitals are destabilized to the same extent. Hence, the degeneracy remains
The charges of ligands are in fact not evenly distributed over a sphere, they are concentrated in certain spaces around the metal center
- Some ligands experience more repulsion from the d-orbital electrons than others based on the geometric structure of the complex
- Since ligands approach from different directions, not all d-orbitals interact directly
- These interactions differ in strength, so they are stabilize or destabilize to different degree, resulting in the splitting of orbitals
- We lift the degeneracy by removing the symmetry
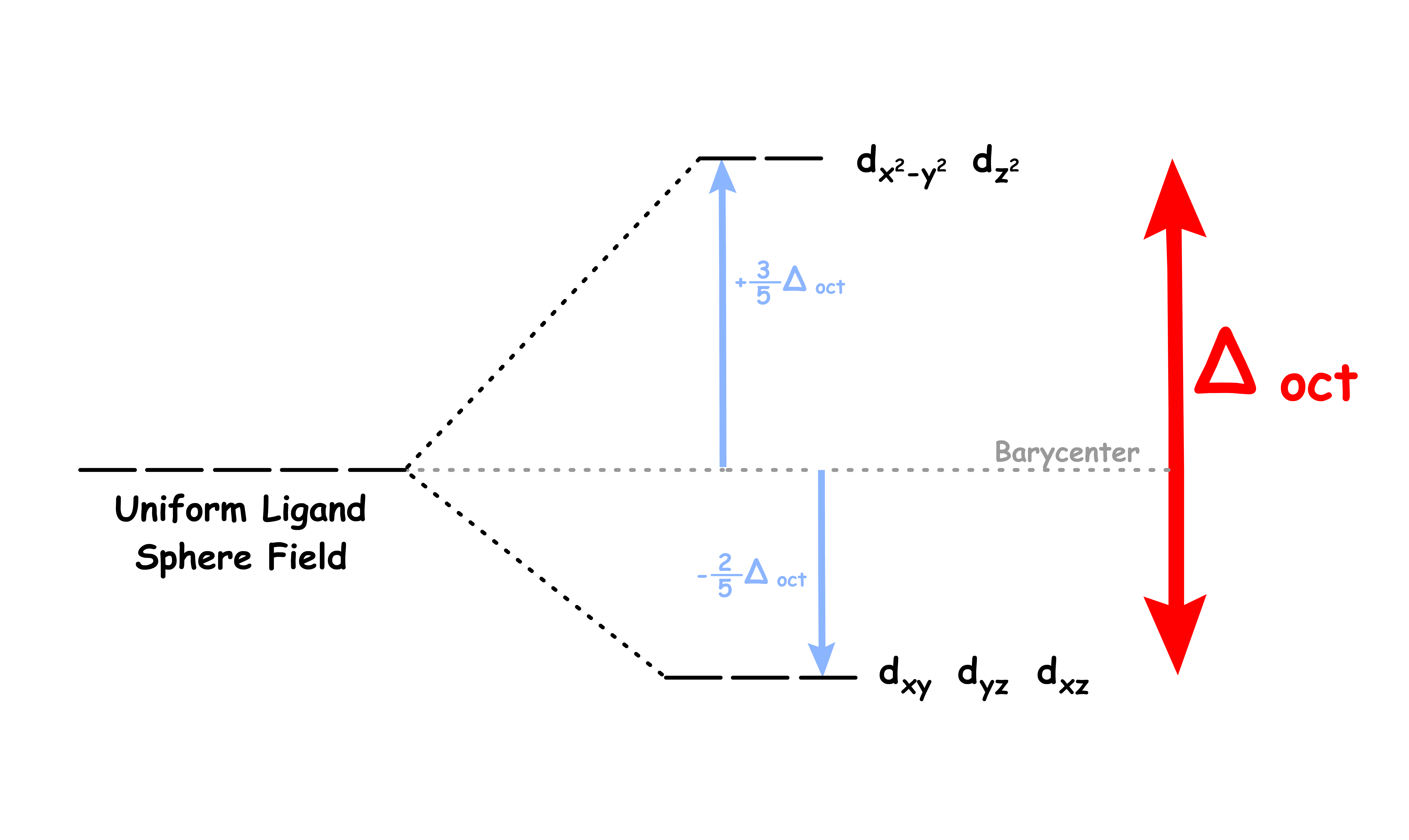
Whether a d-orbital is considered as stabilized or destabilized depend on their relative position with their original energy level in a uniform spherical ligand field
- We denote the energy level that d-orbitals would have had if they were in a spherical ligand field as the Barycentre
- d-orbitals with energy level higher than the Barycenter after splitting are considered as destabilized
- d-orbitals with energy level lower than the Barycenter after splitting are considered as stabilized
There must be an energy balance
- The magnitude of the destabilization energy of d-orbitals must be counterbalanced by the same magnitude of stabilization energy of d-orbitals
- The net stabilization or destabilization of all 5 orbitals must be added up to 0
- The average energy of the five split d-orbitals is the same as the Barycenter
¶ Arrangement of Electrons
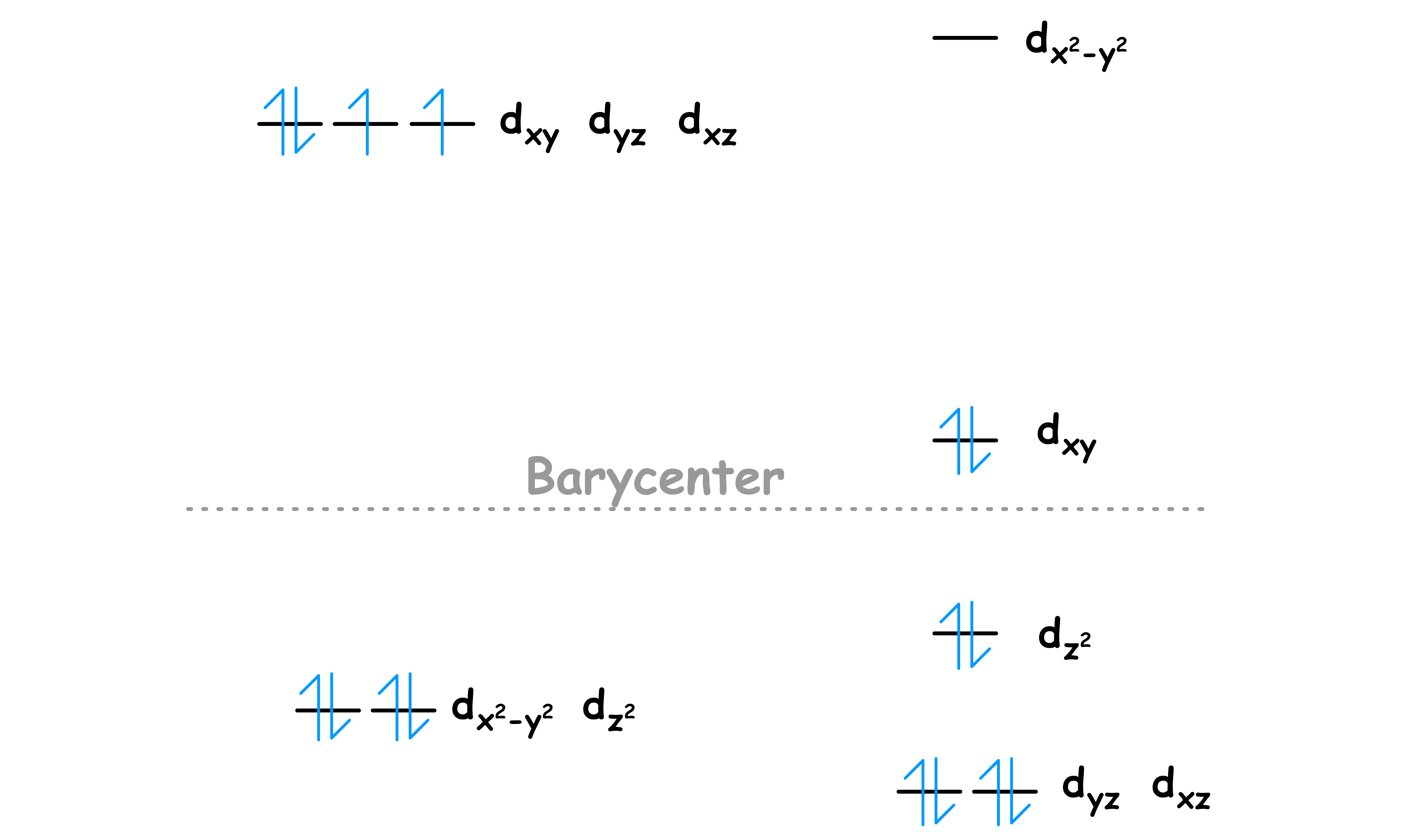
According to the Aufbau principle, electrons are filled from lower to higher energy orbitals
When one or a whole set of degenerate orbitals are half-filled ( all the electrons ) are unpaired, the next electron can be either added as a spin-pair in the same level or be added as an unpaired electron in the next highest orbital
No matter how you add the extra electron, the action will always cost you some energy
- When the extra electron is added as a spin-pair, there will be an additional spin-pairing energy ( P ) due to electron repulsion
- When the extra electron is promoted to the next level, it will be less stabilized or even destabilized
The system is always trying to achieve the lowest overall energy possible, so how the electron will be added depends on which action cost the lowest amount of energy
- If the pairing energy is greater than the promotion energy, the electron will be promoted
- If the crystal field splitting energy ( promotion energy ) is greater than the pairing energy, the electron will be paired
There are two possibilities
- Situations that allows for the least amount of unpaired electrons are refered to as low spin
- Situations that allow for the most number of unpaired electrons are refered to as high spin
The pairing energy is dependent on a given metal and its oxidation state
- The crystal field splitting energy is dependent on a given metal, its oxidation state and the type of ligands used
The stability of the electronic arrangement of a certain geometry can be quantitatively described using the Crystal Field Stabilization Energy ( CFSE )
- CSFE describes the stabilization of a particular arrangement of ligands ( geometry ) with respect to the spherical ligand field
¶ Factors affecting the Crystal Field Splitting Energy
The crystal field splitting energy is denoted as Δgeometry
Δ increases with increasing oxidation state of the metal center
- As we increase the oxidation state of the metal, the center becomes more positively charged and the ligands are pulled in closer
- The close proximity allows for a stronger interaction between the d-orbitals and the ligands
Δ increases down the group of transition metal in the Periodic Table
- As we go down the group, the d-orbitals of the transition metal becomes larger
- The large d-orbitals can extent further, thus allowing better interactions with the ligands
- Note that the pairing energy also decreases down the group due to a smaller electronic repulsion in a larger orbital
- These two effects causes low spin to be more favorable for metal complexes in the lower rows
Spectrochemical Series
- Ligands that produce a large splitting are called strong field ligands, and those that produce a small splitting are called weak field ligands
¶ Coordination Number 6
¶ Octahedral Complex
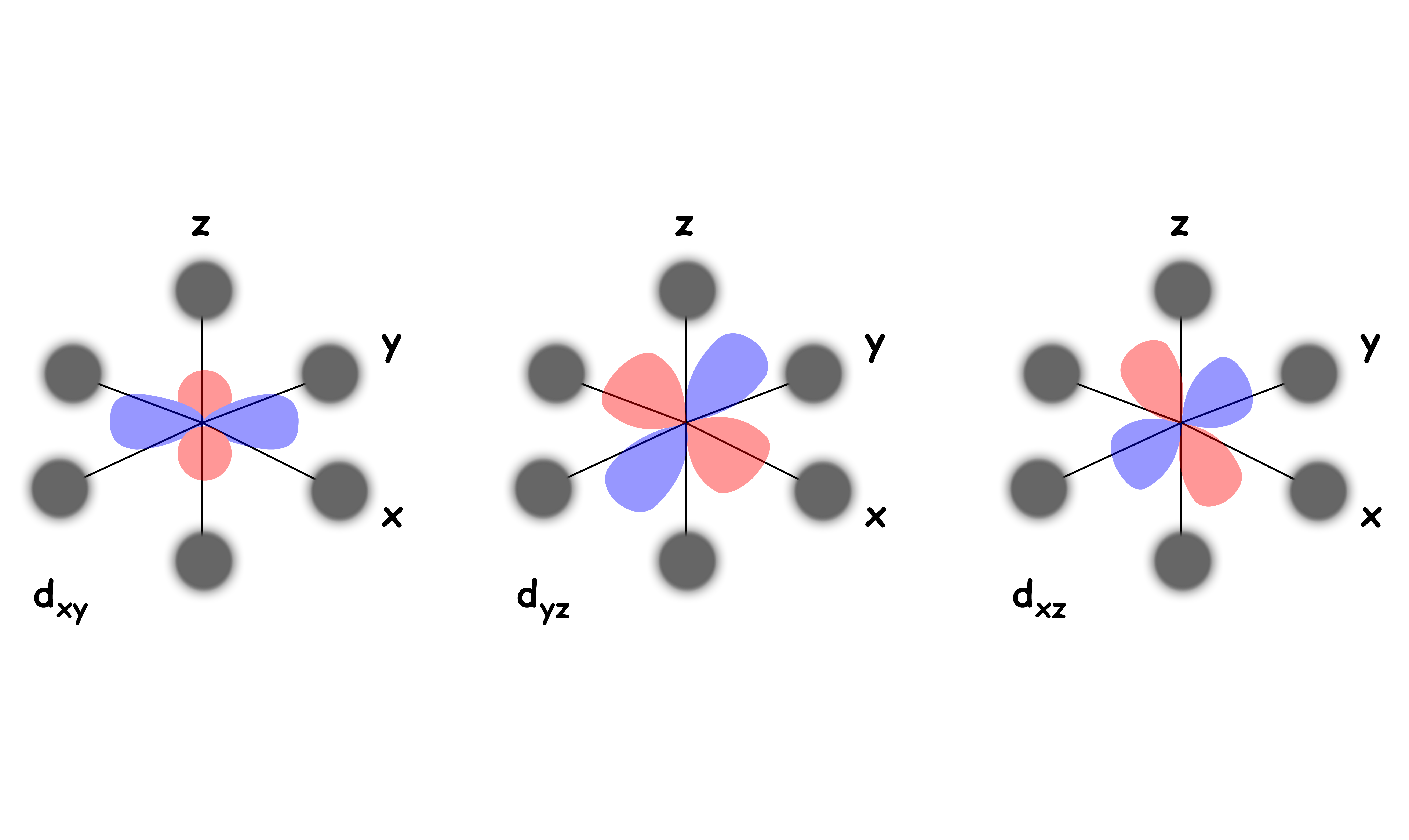
In an octahedral complex, there are six ligands attached to the central transition metal
Both and are pointing directly towards the negatively charged ligands
- They feel a particularly strong repulsive force
- They are destabilized to a higher degree relative to the Barycenter
The , and orbitals are not pointing directly to the negatively charged ligands
- They feel a relatively weak repulsive force
- They are destabilized to a lesser degree and is stabilized relative to the Barycenter
The difference in the degree of stabilization causes the d-orbitals to split in two degenerate sets
We can refer to the and orbitals as the eg set and the , and orbitals as the t2g set
- The eg set is destabilized by 0.6 Δoct
- The t2g set is stabilized by 0.4 Δoct
The CFSE of octahedral complexes can be calculated using this formula:
¶ Coordination Number 4
¶ Tetrahedral Complex
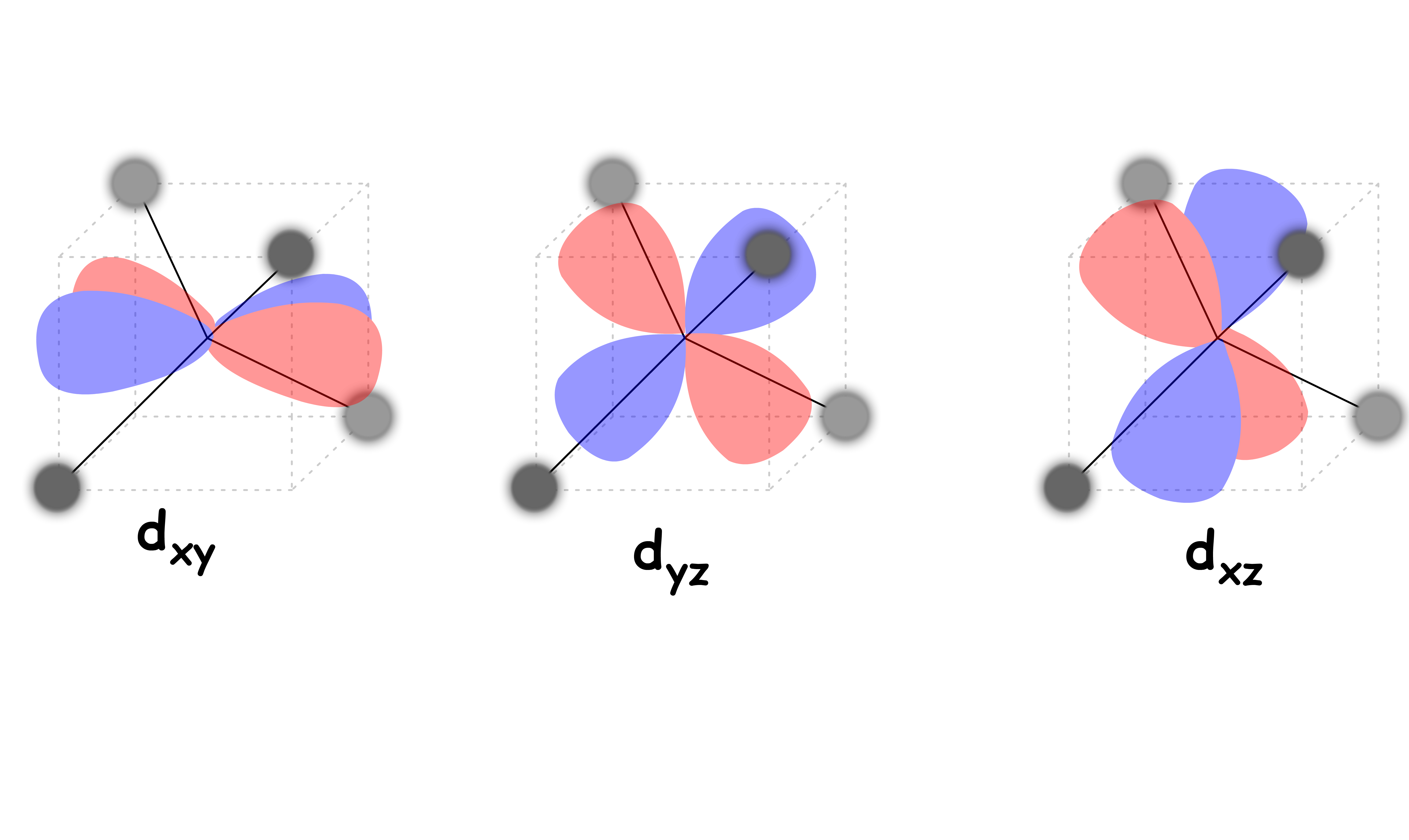
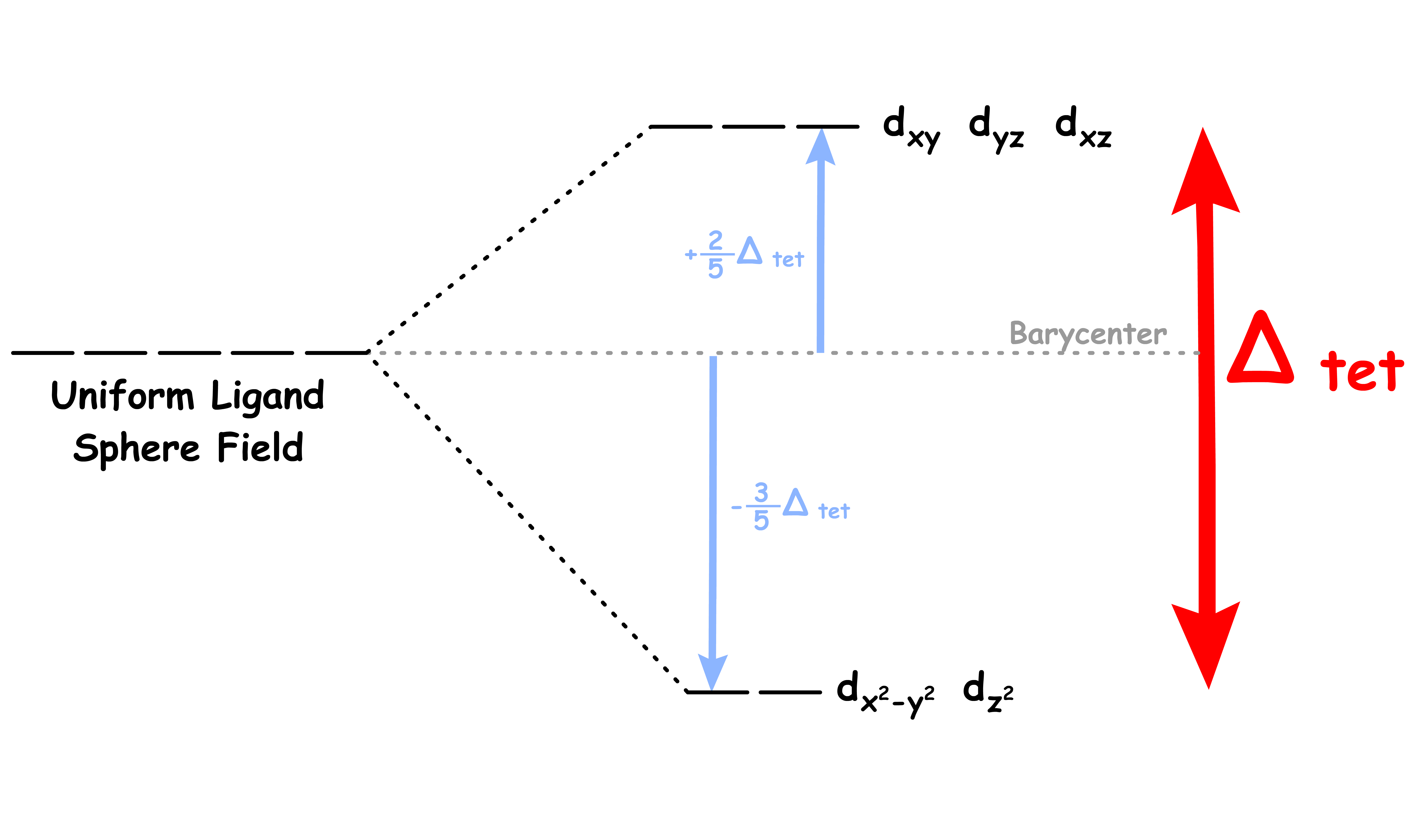
In an tetrahedral complex, there are four ligands attached to the central transition metal
Although the , and orbitals are not pointing directly to the ligands, they overlap to a significant degree
- They feel a particularly strong repulsive force
- They are destabilized to a higher degree relative to the Barycenter
The and orbitals are not in close proximity to the ligands
- They feel a relatively weak repulsive force
- They are destabilized to a lesser degree and is stabilized relative to the Barycenter
The difference in the degree of stabilization causes the d-orbitals to split in two degenerate sets
We can refer to the and orbitals as the e set and the , and orbitals as the t2 set
- The e set is destabilized by 0.6 Δoct
- The t2 set is stabilized by 0.4 Δoct
The CFSE of octahedral complexes can be calculated using this formula:
Since none of the d-orbitals directly points at the ligands, the interaction between them is relatively weak
- Δtet is relatively small for all tetrahedral complexes
- Low spin is a much preferred ( the only ) arrangement we see in tetrahedral complexes
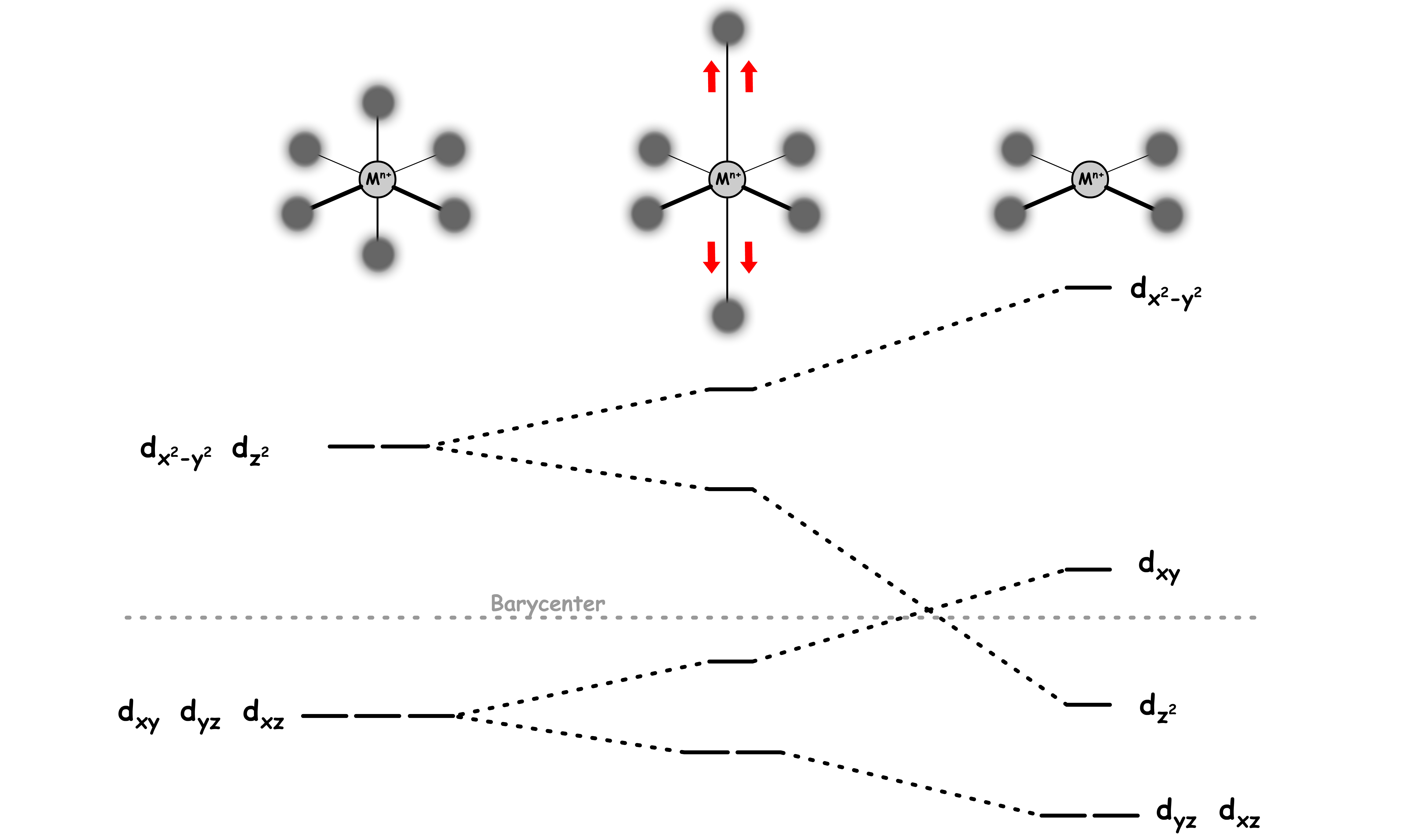
¶ Square Planar
In a square planar complex, there are four ligands attached to the central transition metal
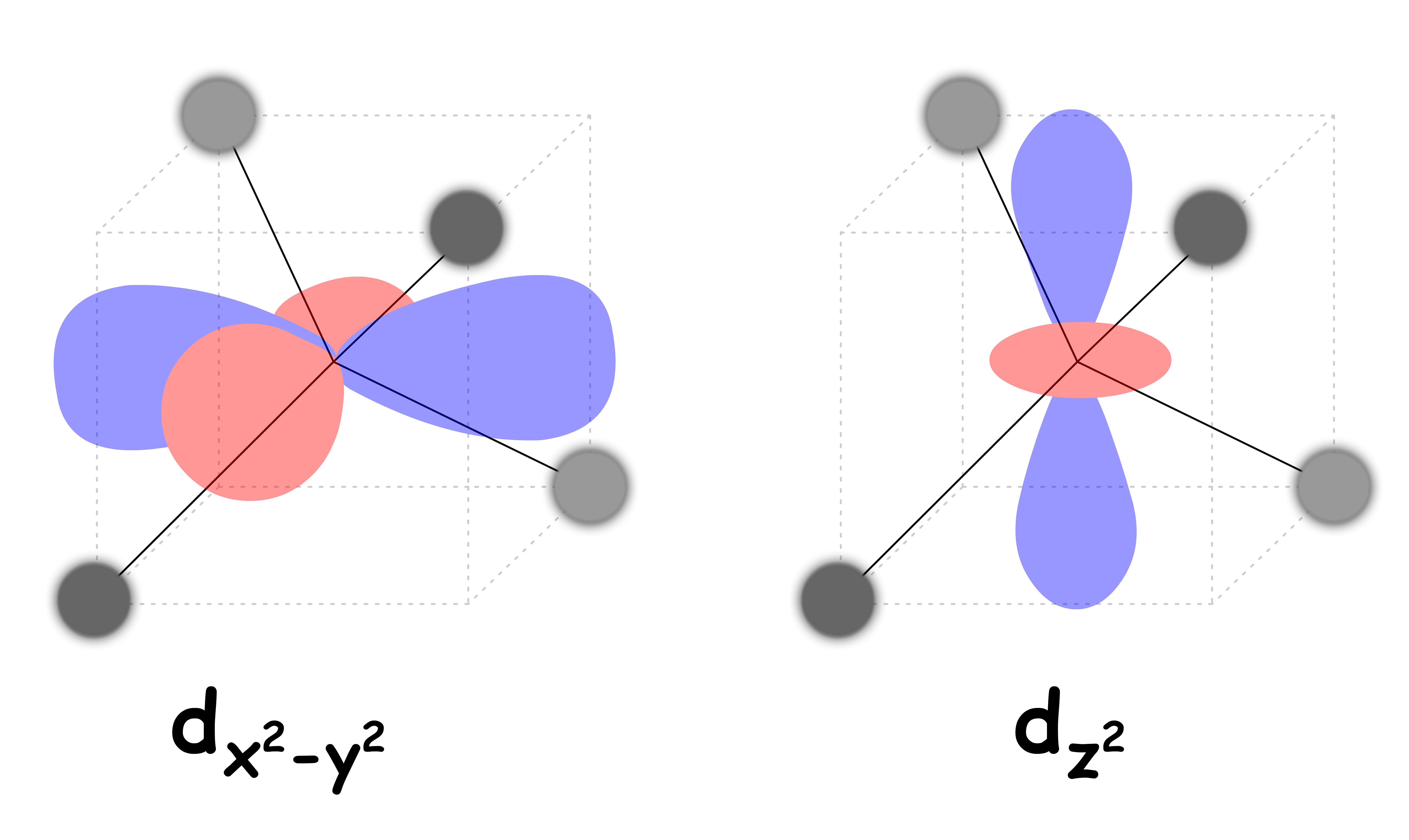
To model the splitting of d-orbitals in a square planar complex, we can take references from a octahedral model
- We can obtain a square planar geometry by removing two ligands of an octahedral complex along the z-axis
When we start to pull away the two ligands along the z-axis, the octahedral ligand field is warped into a tetragonally distorted ligand field
As the two orbitals are being pulled away, the steric hinderance along the z-axis decreases
- This allows the other ligands to get closer to the center, causing their bond with the metal center to shorten
- The and orbitals have a better interaction with those orbitals, thus leading to a further destabilization
The two ligands along the z-axis is further away than they are in a octahedral geometry
- The orbitals with a z-component will feel less repulsion from the ligands
- The , and orbitals are stabilized
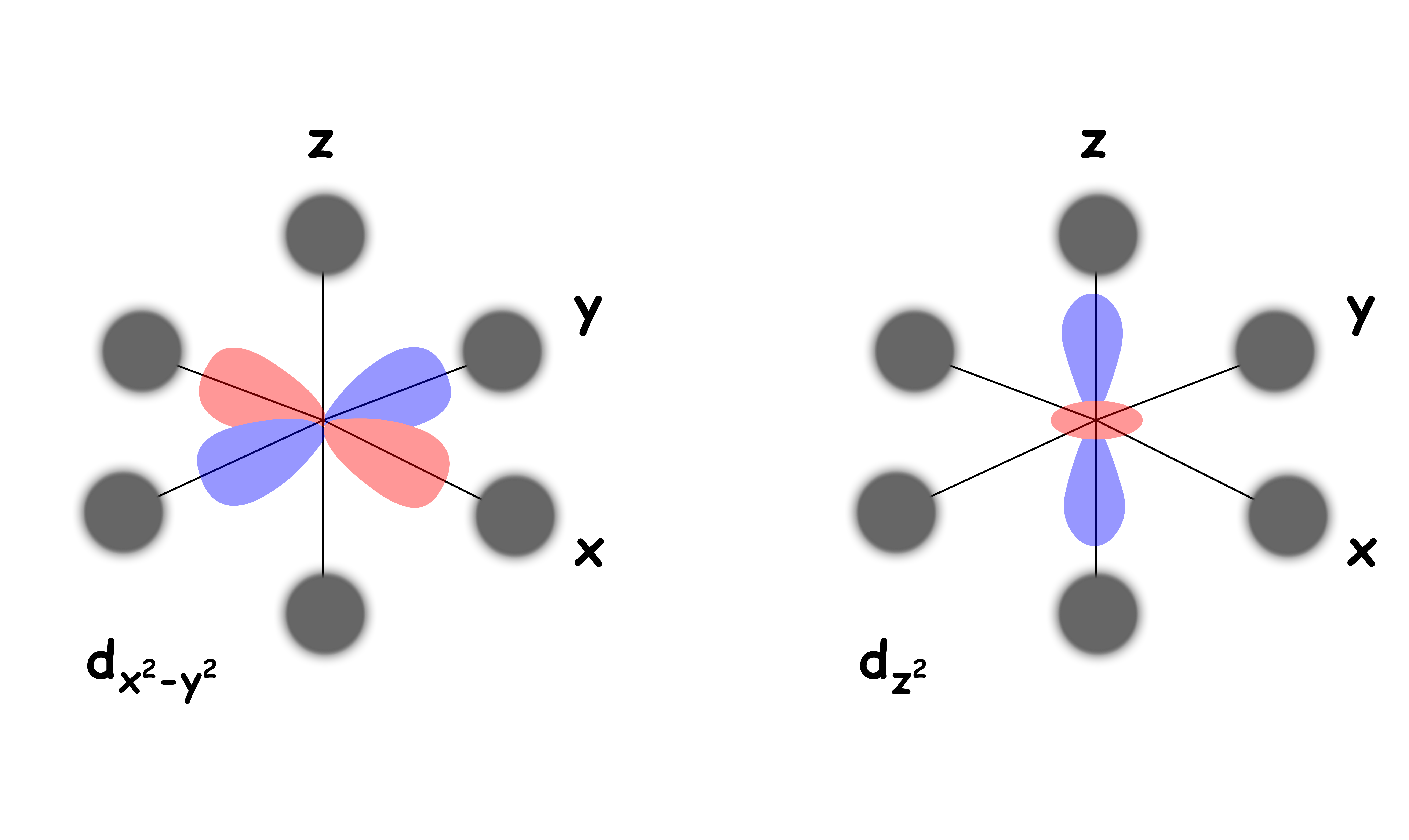
When the two ligands are kept being pulled away when they are infinitely far away from the metal center, the complex will adopt a square planar geometry
- The orbital is stabilized so much that it is now below the Barycenter
- The orbital is destabilized so much that it is now above the Barycenter
However, for purely σ-donating ligands the orbital is still higher in energy than the , dxz and dyz orbitals because of the torus shaped lobe of the orbital
- The ring bears electron density on the x- and y-axes and therefore interacts with the filled ligand orbitals
¶ Choosing between Tetrahedral and Square Planar
When a metal complex has a coordination number of 4, it can adopt either the tetrahedral or square planar geometry
Tetrahedral geometry is much more common than square planar geometry because it offers a far better steric environment
- In a tetrahedral complex, each ligand is 109.5° away from each other
- In a square planar complex, the ligands are confined in the same plane and each of them are only 90° away from the other
Since tetrahedral geometry are far better than square planar in terms of spatial arrangement and steric
- The only way square planar can even exist is to offer a better stabilization in terms of electronic configuration
Square planar is particularly stable for d8 complexes
- Having 8 electrons in the square planar geometry rather than the tetrahedral geometry results in a better electronic stabilization overall
A 4-coordinate d8 complex will likely prefer the square planar geometry over the tetrahedral geometry if the crystal splitting energy, Δ, is large
- For 3d8 complexes, strong field ligands are required to adopt the square planar geometry
- For 4d8 and 5d8 complexes, the square planar geometry is preferred regardless of their ligands
We can force a 4-coordinate complex to adopt a certain geometry
- Bulky ligands ensure that the complex has to be tetrahedral
- A macrocyclic ligand can force the complex to become square planar